Teoremas de conservación en Mecánica Analítica

Departamento: Física Aplicada III
Mecánica Racional (Ingeniería Industrial)
Exámen Cuatrimestral: 17-01-08
Teoría: Teoremas de Conservación en Mecánica Analítica
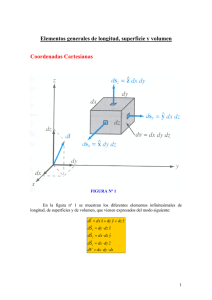
Aplicación.El sistema de la figura representa una partícula P de masa m, contenida en el plano horizontal Oxy,
obligada a moverse por el interior de un tubo OA, liso y de masa despreciable, que está articulado en
el origen O. La posición del punto P viene dada por las coordenadas {ρ,θ}. Aplicando los teoremas
enunciados anteriormente, deduzca razonadamente las magnitudes que se conservan en los tres
supuestos siguientes:
1. Las coordenadas {ρ,θ} son libres.
2. El tubo se mueve de modo que θ (t ) = ω0t , donde ω0 es una constante conocida.
y
A
P
ρ
θ
O
x
El tubo se mueve de modo que θ (t ) = α t 2 / 2 , donde α es una constante conocida.
3.
Teoría
Aunque solo es necesario formular el enunciado de los teoremas de conservación, se procederá a justificar la conservación de las
magnitudes involucradas partiendo de las ecuaciones de la Dinámica Analítica e insistiendo en las condiciones que han de cumplir los
sistemas mecánicos.
Ecuación Simbólica de la Dinámica Analítica
A partir del Principio de los Trabajos Virtuales y del de D’Alambert se obtiene la ecuación fundamental de la Dinámica Analítica,
G
∑ (F
G
G
− mk ak ⋅ δ rk = 0
(1)
)
k =1
G
donde Fk (k=1..n) representa las fuerzas activas; las vinculares no aparecen porque se suponen ligaduras ideales y en ese caso el
trabajo virtual debido a estas fuerzas es nulo (Principio de Ligaduras Ideales).
N
k
Teorema de Conservación de la Energía Mecánica en Dinámica Analítica
Cuando los vínculos son esclerónomos –independientes del tiempo–, algunos de los desplazamientos virtuales del sistema pueden
coinciden con los desplazamientos reales; en este caso (1) nos conduce( 1 ) al teorema de la energía de la dinámica vectorial
d 'W = d T
(2)
Si todas las fuerzas activas son conservativas, el trabajo d’W se emplea en cambiar la energía potencial con lo cual
d (T + U ) = 0 ó T+U=E (cte.)
Conclusión
“Cuando las fuerzas activas son conservativas y las ligaduras son ideales y esclerónomas, la Energía Mecánica, E=T+U, se
conserva ”
Teoremas de Conservación de los momentos conjugados ó generalizados pk =
∂T
∂ q k
La ecuación (1) expresada en coordenadas curvilíneas es
⎛ d ∂T
∑ ⎜ d t ∂ q
k
⎝
−
k
⎞
∂T
− Qk ⎟ dqk = 0
∂ qk
⎠
(3)
donde T representa a la energía cinética, qk (k=1..n) las coordenadas curvilíneas –no necesariamente independientes– y Qk las fuerzas
generalizadas. En el caso de coordenadas independientes ha de anularse cada uno de los coeficientes entre paréntesis, que
acompañan a dqk y conduce a n ecuaciones, llamadas ecuaciones de Lagrange, donde n es el número de grados de libertad
d ∂T ∂T
−
= Qk , k=1..n (grados de libertad)
d t ∂ q k ∂ qk
(4)
Caso general
a)
Si una coordenada qj no aparece en la energía cinética,
∂T
= 0 , y además Qj=0 –se anula la fuerza generalizada correspondiente– ,
∂ qj
d ∂T
∂T
= 0 , que nos conduce a pk =
= cte.
d t ∂ q j
∂ q j
queda
Conclusión:
“Cuando los vínculos son ideales ,las coordenadas independientes, en la energía cinética no aparece una coordenada qj y se anula
la fuerza generalizada correspondiente Qj, el momento conjugado pj se conserva”
1
G
∑F
k
k
G
⋅ δ rk = d `W ,
G
∑m a
k
k
k
G
⋅ δ rk = δ T
Teoremas de conservación en Dinámica Analítica
b)
Caso de sistemas con fuerzas activas conservativas y no conservativas
Con estas nuevas condiciones (4) se expresa mediante las ecuaciones
d ∂L ∂L
−
= QkN .C .
d t ∂ qk ∂ qk
donde QkN .C . se refiere a las fuerzas generalizadas no conservativas y L=T-U es la lagrangiana del sistema.
Estas ecuaciones son formalmete iguales a las anteriores y se reducen a ellas cambiando L por T,
Conclusión
“Cuando los vínculos son ideales, las coordenadas independientes,la coordenada qj es cíclica( 2 ) y se anula la fuerza generalizada
correspondiente QkN .C . , el momento conjugado pj se conserva”
En el caso particular de sistemas donde todas las fuerzas activas son conservativas (denominados sistemas conservativos), obviamente
cumple QkN .C . = 0
Conclusión
“Cuando los vínculos son ideales, las coordenadas independientes, la coordenada qj es cíclica y todas las fuerzas activas son
conservativas, el momento conjugado pj se conserva”
Caso de coordenadas dependientes con vínculos geométricos Ψ (q1...qn , t ) = 0 , ó cinemáticos del tipo g ≡ a1 q1 + ... + an qn + b = 0
c)
Aplicando el principio de liberación, podemos sustituir el vínculo por la fuerza vincular correspondiente. Esta fuerza vincular viene
dada por las expresiones Q *j = λ
∂Ψ
∂g
si los vínculos son geométricos, y Q *j = λ
si son cinemáticos
∂ q j
∂ qj
Las ecuaciones de Lagrange adoptan la forma
d ∂L ∂L
∂Ψ
∂g
−
= QkN .C . + λ
+μ
d t ∂ qk ∂ qk
∂ qk
∂ qk
Conclusión para el caso de fuerzas activas conservativas y no conservativas
“Cuando los vínculos son ideales, la coordenada qj es cíclica, se anula la fuerza generalizada correspondiente QkN .C . y q j , q j no
aparecen en las ecuaciones de ligadura, el momento conjugado pj se conserva”
Los casos y condiciones anteriores pueden resumirse en la siguiente tabla
∂L
∂T
=
∂ qk ∂ qk
Coordenadas Dependientes
Ψ j (qk ) = 0 , ó, Ψ j (qk ) = 0
Casos en que se conserva el momento conjugado ó generalizado pk =
Vínculos ideales +
Coordenadas Independientes
F.A..: Conservativas
∂L
= 0,
∂ qk
F.A. :No Conservativas
∂T
=0
∂ qk
,
QkN .C = 0
,
∂Ψ
=0,
∂qk
F.A..: Conservativas +
No Conservativas
∂L
=0
∂ qk
,
QkN .C = 0
,
∂Ψ
=0,
∂qk
∂Ψ
∂Ψ
∂L
=0
=0,
=0,
∂ qk
∂qk
∂qk
∂Ψ
=0
∂qk
∂T
=0
∂ qk
,
∂Ψ
=0
∂qk
,
,
∂L
=0
∂ qk
QkN .C = 0
,
QkN .C = 0
Teorema de conservación del hamiltoniano
La función de Hamilton H se define mediante la expresión
H = ∑ pk qk − L
k
Cuando los vínculos además de ser ideales son esclerónomos H=T+U, coincide con la energía mecánica del sistema.
Para el caso de vínculos ideales, coordenadas independientes y fuerzas activas conservativas, H y L están relacionados por la ecuación
dH
∂L
=−
dt
∂t
Si además t no aparece en la lagrangiana
∂L
= 0 y en consecuencia H es constante.
∂t
Conclusión
“Cuando los vínculos son ideales, las coordenadas independientes ,todas las fuerzas activas conservativas y el tiempo no aparece
en la lagrangiana, el hamiltoniano se conserva”
2
Una coordenada qj se dice cíclica, si no aparece en la lagrangiana
∂L
=0
∂ qj
Pag. 2 / 3
Teoremas de conservación en Dinámica Analítica
Aplicación
Análisis previo
Se trata de un sistema formado por una sola partícula con vínculos ideales y no existen fuerzas activas ó bien estas no cambian la
energía potencial, con lo cual el sistema puede considerarse conservativo, lo que no significa que tenga que conservarse la energía.
Cálculo de la energía cinética
1
1
G 2 G
G
G
T = m ( v P ) , v P = ρ uρ + ρ θ uθ , T = m ( ρ 2 + ρ 2 θ 2 )
2
2
Cálculo de la energía potencial: U=0, porque el plano es horizontal
Lagrangiana: L= T
Solución de la aplicación:
1. Las coordenadas {ρ,θ} son libres
El sistema posee dos grados de libertad descritos por las coordenadas anteriores
Conservación de la Energía
La energía mecánica es constante porque los vínculos son ideales y en este caso esclerónomos (independientes del tiempo)
1
T = m ( ρ 2 + ρ 2 θ 2 ) = cte.
2
Conservación de momentos conjugados
∂T
El momento conjugado pθ =
es constante, porque los vínculos son ideales, las coordenadas {ρ,θ} independientes, la fuerza
∂ θ
generalizada Qθ = 0 (ó bien el sistema puede considerarse conservativo) y la coordenada θ es cíclica.
m ρ 2θ = cte,
∂T
, no es constante porque la coordenada ρ no es cíclica (aparece en L)
∂ ρ
Conservación del hamiltoniano
H=E=T, porque los vínculos son ideales y esclerónomos y las fuerzas activas pueden considerarse conservativas.
El momento conjugado pρ =
2. El tubo se mueve de modo que θ (t ) = ω0t .
En este caso se tiene un solo grado de libertad y una sola coordenada libre ρ
Haciendo θ = ω0 , la energía cinética se expresa
1
T = m ( ρ 2 + ρ 2 ω 2 )
2
Conservación de la Energía Mecánica
Esta magnitud no se conserva porque el vínculo θ (t ) = ω0t es reónomo y para que E sea constante es preciso que los vínculos sean
ideales y esclerónomos
Conservación de momentos conjugados
∂T
El momento conjugado pρ =
no es constante porque la coordenada ρ no es cíclica (aparece en L) y el momento conjugado
∂ ρ
∂T
no puede considerarse porque la coordenada θ no es libre ó independiente.
∂ θ
Conservación de H
El hamiltoniano se conserva porque los vínculos son ideales, la coordenada ρ es independiente, el sistema puede considerarse
conservativo y el tiempo no aparece en L.
H = pρ ρ − L
pθ =
1
1
H = m ρ 2 − m ( ρ 2 + ρ 2ω02 ) = m ( ρ 2 − ρ 2ω02 ) = cte.
2
2
En este caso de vínculo reónomo H no coincide con la energía.
El tubo se mueve de modo que θ (t ) = α t 2 / 2
1
Este caso difiere del anterior en que T = m ( ρ 2 + ρ 2 α 2 t 2 ) en consecuencia, igual que en el caso anterior, no se conserva ni la
2
energía mecánica ni el momento conjugado pρ .
3.
El hamiltoniano, no coincide con la energía mecánica porque hay un vínculo reónomo (no esclerónomo) y tampoco es constante
porque en T aparece el tiempo-
Pag. 3 / 3