Econometría II

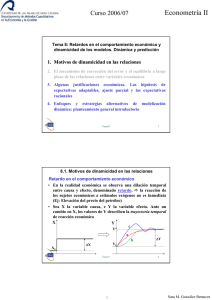
Econometría II
Curso 2006/07
Tema 9: Modelos con retardos distribuidos (I)
1. Análisis de los efectos dinámicos en un modelo
de retardos distribuidos
2. La distribución de retardos
Tema 9
1
9.1. Análisis de los efectos dinámicos en un modelo con
retardos distribuidos
• Objetivo: Estudiar la forma de una relación causal dinámica.
Situación de equilibrio Ö Evolución
• Interés: Evolución de la endógena ante cambios en la exógena
(más que el efecto total, cómo se distribuye el mismo)
• Tipos de modelos dinámicos:
cAutorregresivo
dDe retardos distribuidos
ÖSe puede transformar 1 en otro
Paso de c a d: Sustituir las Yt-k por los valores del modelo
• Ejercicio: Transformar en modelo de retardos distribuidos
Yt = α + β0 Xt + β1Xt−1 +γYt−1 +εt
Tema 9
1
2
Sara M. González Betancor
Econometría II
Curso 2006/07
• Los modelos con retardos distribuidos son un caso concreto
de modelos dinámicos. Son la metodología econométrica
clásica para trabajar con modelos de regresión dinámicos.
• Suelen suponer una distribución o pauta determinada de los
retardos (para poder estimar los parámetros). Esta distribución
proviene de planteamientos de base económica (expectativas
adaptables, ajuste parcial, corrección del error...)
• Tipos de modelos con un retardo distribuido:
Infinito:
Finito:
Yt = α + β0 Xt + β1Xt−1 + β2 Xt−2 + ... + ut
Yt = α + β0 Xt + β1Xt−1 + β2 Xt−2 +...+ βk Xt−k + ut
Tema 9
3
• Ejemplos gráficos de comportamiento dinámico:
β
β1 2
Sea un modelo con
∆Y=Σβj
β0
distribuidos
Yt retardos
(finito o infinito).
∆X=1
β son los coeficientes
de reacción o coeficiente
de respuesta a un
impulso.
Xt Los
t0t1 t2t3
t0+m
Yt
∆X=1
t0
Xt
t
t0+m
Tema 9
2
Indican el grado de
variación de Y provocado
por un aumento unitario
de X
4
Sara M. González Betancor
Econometría II
Curso 2006/07
• Significado económico de los β = multiplicadores dinámicos
Yt = α + β0 Xt + β1Xt−1 + β2 Xt−2 + ... + ut
Multiplicador de impacto:
Indica
el
grado
de
variación de Yt ante una
variación unitaria de Xt
M0 =
Multiplicador intermedio de
retardo k: Indica el grado
de variación de Yt ante una
variación unitaria de Xt-k
dYt
= β0
dXt
Mk =
dYt
= βk
dXt−k
Multiplicador total: Efecto total sobre Y ante una variación
unitaria de Xt
MT = β0 + β1 + β2 + ...
Perfil Temporal: Representación gráfica de multiplicadores
Los multiplicadores se suelen normalizar para comparar
perfiles de diferentes variables Ö Multip. Normalizado
Tema 9
5
Ejercicios
1.
Estudia los multiplicadores del siguiente modelo (multiplicador de impacto,
intermedios, total y normalizados) así como su perfil temporal.
Yt = −0.28 + 0.13Yt −1 + 0.24 X t + u t
2.
Se sabe que los beneficios de una empresa dependen de la inversión realizada
en publicidad en el mismo período de tiempo y en los últimos tres períodos de
tiempo. El equipo de dirección de la empresa está estudiando incrementar
solamente en este año los gastos en publicidad. Es decir, en este año se
incrementa la publicidad en una cierta cantidad y los años siguientes se vuelve
al nivel del período anterior. Determina bajo qué condiciones debe realizar la
inversión, sabiendo que si guardase ese dinero en el banco se lo pagarían con
un tipo de interés por período de un r%
3.
Supongamos que, para el ejercicio anterior, r=10% y el modelo estimado es
Yˆt = 25 + 0.4 X t + 0.7 X t −1 + 0.3 X t − 2 + 0.1X t − 3
en donde Y representa a los beneficios y X a los gastos en publicidad. ¿cuál
sería su decisión?
Tema 9
3
6
Sara M. González Betancor
Econometría II
Curso 2006/07
Tema 9: Modelos con retardos distribuidos (I)
1. Análisis de los efectos dinámicos en un modelo de
retardos distribuidos
2. La distribución de retardos
Tema 9
7
9.2. La distribución de retardos
• Hipótesis: Todos los multiplicadores son positivos y en el
infinito toman valor cero.
Yt = α + β 0 X t + β1 X t −1 + β 2 X t − 2 + ... + ε t
• Análisis más exhaustivo Ö Binomio (retardo, multiplicador)
= Distribución de frecuencias
: Variable a estudiar
:Frecuencia Absoluta
Ö Estudiar sus características descriptivas (media, mediana,
moda, dispersión, asimetría, curtosis, ... ) para sintetizar la
información.
• Objetivo: Estudiar la distribución de retardos Æ
Multiplicadores = Frec. Absol. (importancia de cada retardo
al definir la modificación de la variable ‘efecto’ por la ‘causa’)
Tema 9
4
8
Sara M. González Betancor
Econometría II
Curso 2006/07
Retardo Multiplicador
0
1
2 ...
β0
β1
β 2 ...
wi =
βi
∑ βi
= ponderación
i
Retardo medio: tiempo medio que, un cambio en X tarda en
wi ⋅ i
producir modificaciones sobre Y ⇒ RM =
∑
i
Retardo mediano: tiempo que, por término medio, es
necesario para que transcurra el 50% de la reacción
r
Primero que cumpla:
∑ w ≥ 0.5
i
i
Varianza: dispersión en el tiempo de los efectos de X sobre Y
VR = ∑ wi ( i − RM )
2
i =0
Tema 9
9
Coeficiente de Asimetría: Es el de Fisher
A=
∑ w ( i − RM )
i =0
⎛
⎜
⎝
3
i
∑ w ( i − RM )
2
i
i =0
⎞
⎟
⎠
3
Coeficiente de Apuntamiento: Es el coeficiente de curtosis de
Fisher
4
C=
∑ w ( i − RM )
i =0
⎛
⎜
⎝
i
2 ⎞
wi ( i − RM ) ⎟
∑
i =0
⎠
Tema 9
5
4
−3
10
Sara M. González Betancor
Econometría II
Curso 2006/07
Ejercicios
4.
Calcular el retardo medio y mediano para el siguiente modelo
Yt = 0.28 + 0.43 X t −1 + 0.39 X t −2 + 0.30 X t −3 + 0.18 X t −4 + 0.12 X t −5 + ut
5.
Calcular el retardo medio y mediano del ejercicio 1.
6.
Calcular el retardo medio, el retardo mediano y la variabilidad relativa de la
distribución de retardos estimada en el ejercicio 3.
7.
La teoría económica postula una relación entre la demanda de dinero y la tasa
de interés óptima de la forma: Demandat = α + β ⋅ tipoóptimot* + ut
Dado que esta ecuación contiene un tipo de interés óptimo o esperado (en el
sentido de anticipado) y que éste no es directamente observable, se propone
una generación de expectativas basada en la hipótesis de expectativas
∗
∗
∗
adaptativas de la forma: X t − X t −1 = γ X t − X t −1
(
)
en donde el * indica el valor óptimo, y la variable sin él, el valor observado.
Mida la velocidad que existe entre los cambios en los tipos de interés y la
demanda de dinero
Tema 9
6
11
Sara M. González Betancor