N - Vertebrados

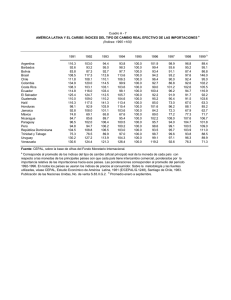
Ecología de la Parte Peces.
VIAJE DE CAMPAÑA CATEDRA DE ZOOLOGIA III
(VERTEBRADOS), FCNyM, UNLP. AÑO 2014.
Autores: Martin Montes, Adriana Almirón, Jorge Casciotta.
Cuando se emprende un estudio se deben decidir que metodologías usar, y decidir si
realizar un “muestreo” o un “censo”. En un censo se registran todos los individuos que
forman parte de la población/comunidad (según sea el objetivo del trabajo), mientras que en
un muestreo se toma una pequeña cantidad de individuos que representan la realidad. Como
un censo trae aparejados problemas éticos y metodológicos, se prefiere muchas veces
realizar un(os) muestreo(s).
MÉTODOS DE ESTUDIO DE POBLACIONES
Otolitos
Curvas de crecimiento
Medidas
Parámetros poblacionales (número de hembras, estados reproductivos (diagnosis de
diferentes órganos)
Cristalino
Parásitos, lesiones
MÉTODOS DE ESTUDIO DE COMUNIDADES1
Los índices de diversidad consideran dos factores: riqueza de especies, que es el
número de especies y uniformidad (equitabilidad), esto significaría determinar el grado de
abundancia proporcional de las especies entre sí. Muchas de las diferencias entre índices
subyacen en el peso relativo que dan la uniformidad y la riqueza de especies. Hay tres tipos
de categorías principales
a- Índices de riqueza de especies.
a1. Índice de Margalef.
b- Modelos de abundancia de especies.
c- Índices basados en la abundancia proporcional de especies.
1
Extraido de Magurran (1988)
1
c1. Índice de Shannon-Wiener.
c2.- Índice de Diversidad .
c3.-El Índice de Brillouin (HB).
Medidas de Dominancia
c4.- Índice de Simpson.
c.5.- Índices de Berger-Parker.
Índices deSimilitud
c6.- Medida de similaridad de Jaccard.
c7.-Medida de similaridad de Sorenson (datos cualitativos).
c8.- Medida de similaridad de Sorenson (datos cuantitativos).
c9.- Medida Morisita-Horn.
a- Índices de riqueza de especies.
Existen una gran cantidad de índices que intentan medir la riqueza numérica de
especies, es decir el número de especies por número de individuos especificados. Desde
luego, no siempre es posible asegurar que los tamaños muestreales serán iguales y, cabe
considerar que el número de especies aumenta invariablemente con el tamaño muestreal y
el esfuerzo de muestreo. Para solucionar este problema se ideo una técnica denominada
“rarefacción” que permite calcular el número de especies esperado en cada muestra si todas
las muestras tuvieran igual tamaño.
La mayor crítica a la rarefacción es que conduce a una gran pérdida de información.
La riqueza de especies nos proporciona una expresión comprensible e instantánea de
la diversidad. Sin embargo debe tenerse en cuenta que depende del tamaño muestreal, ya
que al incorporar nuevos individuos es posible que nos encontremos con especies nuevas o
raras. Uno de los índices que se han propuesto y goza de aceptación es:

Índice de Margalef de riqueza especifica:
D mg  S  1 / ln N
Sin embargo, muchos ecólogos confieren mucha importancia a la información sobre
la abundancia relativa de especies y muchas veces la abundancia de especies es una medida
más sensible de distorsiones ambientales que la riqueza de especies por si sola.
b.- Modelos de abundancia de especies
Una distribución de abundancia de especies utiliza toda la información acumulada
en la comunidad y es la descripción matemática más completa de los datos. Aunque los
datos de abundancia de especies frecuentemente se describen mediante una o más de una
2
familia de distribuciones, la diversidad es comúnmente examinada en relación a cuatro
modelos principales. Estos son:




serie geométrica
Serie logarítmica
distribución normal logarítmica
modelo del palo quebrado
Cuando se representa un gráfico rango abundancia (se ordenan las especies de más a
menos abundantes) los cuatro modelos parecen representar una progresión que va desde la
serie geométrica en la que unas pocas especies son dominantes y las restantes
prácticamente raras; pasando por la serie logarítmica y la distribución normal logarítmica
donde las especies con abundancia intermedia llegan a ser más comunes, finalizando en las
condiciones representadas por el modelo del palo quebrado en el que las especies son tan
igualmente abundantes como nunca llega a observarse en el mundo real. Estas
distribuciones pueden hacer referencia al uso del hiperespacio del nicho, donde en la serie
geométrica encontramos una situación de máxima preferencia por el nicho existiendo unas
pocas especies dominantes. El modelo del palo quebrado refleja un caso de mínima
preferencia, con recursos divididos de forma más equitativa.
Este método no constituye una guía mecánica y segura que proporcione el modelo que
mejor describe los datos. Para estar seguro es necesario realizar formalmente las pruebas
matemáticas. Debido que el cálculo es demasiado engorroso para lo que se pretende en este
viaje de campaña, nos limitaremos a graficar cada una de las curvas según las indicaciones
dadas en la siguiente tabla.
Modelo de abundancia de sp.
Serie geométrica
Eje de las abscisas (X)
Especies
Serie Logarítmica
Especies
Normal logarítmica
Especies
Palo quebrado
Secuencia de especies en
escala logarítmica
Eje de las Ordenadas (Y)
Número de individuos
(Abundancias)
Número de individuos
(Abundancias)
Número de individuos
(abundancias) en
logaritmos
Número de individuos
(Abundancias)
c.- Índices basados en la abundancia proporcional de especies
c1.- Índice de diversidad de Shannon-Wiener
Este es un índice basado en la abundancia proporcional de especies. Considera tanto
la uniformidad como la riqueza de especies. Ya que no hace supuestos acerca del aspecto
3
que ofrece la distribución de abundancia de especies subyacente permite referirse a ellos
como índices no paramétricos. Este índice está basado en la lógica de que la diversidad en
un sistema natural puede ser medida de un modo similar a la información contenida en un
código o mensaje.
El índice de Shannon-Wiener, considera que los individuos se muestrean al azar a
partir de una población “indefinidamente grande”, esto es una población efectivamente
infinita. El índice asume que todas las especies están representadas en la muestra. Se
calcula a partir de la ecuación:
H` = −
p lnp
Donde “ln” es el logaritmo natural y
especie i-esima (esto se estima mediante ).
es la proporción de individuos hallados en la
La varianza de H` pude ser calculada:
Var H`=
∑
(
)
(∑
)
+
Para comparar las diferencias significativas entre muestras se utiliza un “t”:
`
t=
(
`
`
` )
Los grados de libertad se calculan utilizando la ecuación
Df = (
y
(
`
` ) ⁄
` )
(
` ⁄
)
son el número total de individuos de las muestras 1 y 2 respectivamente.
El índice de Shannon para un cierto número de muestras se distribuye,
normalmente. Esta propiedad hace posible el uso de estadística paramétrica como por
ejemplo el ANOVA para comparar series de muestras en las cuales se ha calculado la
diversidad. Este índice, sin embargo, es ampliamente discutido por varios autores que
argumentan que es un índice muy insensible a las características de la distribución de
abundancias de especies, dudoso, y sin interpretaciones biológicas directas. Sin embargo,
muchos ecólogos aun prefieren el índice de Shannon por su simplicidad de cómputo.
4
Basados en el Índice de Shannon-Wiener, encontramos medidas de uniformidad
donde la máxima diversidad posible que pudiera tener lugar si todas las especies fueran
igualmente abundantes, se calcula como:
H max ln S
Y la equitabilidad (uniformidad) puede ser calculada:
E=
`
`
= ` ln
Tomará valores de 0 cuando la equitabilidad sea muy baja, y valores de 1 cuando
todas las especies son igualmente abundantes.
Cuando la aleatoriedad de una muestra no puede ser garantizada, como por ejemplo
al utilizar trampas de luz, donde las diferentes especies de insectos son atraídas
diferencialmente por la luz o bien si la comunidad está completamente censada con cada
uno de los individuos representado, el índice de Brillouin sería el más apropiado.
c2.-Índice de Diversidad
Este índice surge del modelo de distribución de datos de la serie logarítmica de
Fisher. El índice puede obtenerse a partir de la ecuación:
=
(1 − )
Y con sus correspondientes límites de confianza obtenidos por:
( ) =
− ln(1 − )
Donde N= número total de individuos y
se estima a partir de la solución iterativa de:
= (1 − )/ [− ln(1 − )]
S= número de especies
En la practica
es casi siempre >0,9 y nunca >1.0.
La importancia de los índices radican es cuan eficaces son para discriminar
localidades o muestras que no son muy diferentes entre sí. Bajo este precepto Taylor
encuentra que el Índice de Diversidad es el mejor discriminador, y próximo viene el
5
índice de Shannon-Wiener, etc. A su vez, el esta menos afectado el tamaño muestreal en
contraposición a lo que ocurre con los índices de Simpson y Shannon.
La única desventaja del es que se basa exclusivamente en S (riqueza de especies)
y N (Número de individuos). Por lo que no puede discriminar en aquellas situaciones en
que S y N permanecen constantes, pero donde si hay cambios en la uniformidad. Pero, estas
son cuestiones netamente académicas, ya que es muy improbable que cualquier colección
de datos genuinos se comporten en este sentido.
c3.-El Índice de Brillouin (HB):
HB 
ln N! ln n i !
N
HB
HB max
1
N!
HB max  ln
sr
r
N
N !
N  1!
S
S
E
    
Dónde:
N= numero de indivíduos
S= numero de espécies
N  la parte entera de N/S y r = N-S N
S
S
 
 
El índice de Brillouin describe una colección de datos conocida. El índice de
Shannon por el contrario ha de estimar la diversidad de la parte no muestreada al igual que
la porción muestreada de la comunidad. El índice de Shannon siempre dará el mismo valor
si se da el mismo número de especies y su abundancia relativa permanece constante. EJ:
Shannon
Brillouin
Muestra 1
10
10
10
10
10
10
10
10
10
10
2.3
2.13
6
Muestra 2
5
5
5
5
5
5
5
5
5
5
2.3
2.01
Para las colecciones, las muestras, al compararse entre sí, cada valor de HB es de
inmediato significativamente diferente de cualquier otra colección. En ciertas
circunstancias el índice de Brillouin puede implicar que la muestra con el número de
individuos más elevado es más diversa que la de mayor riqueza de especies y uniformidad.
Medidas de dominancia
Estos índices ponderan según la abundancia de las especies más comunes más que a
partir de una medida de riqueza de especies:
c4.- Índice de Simpson
Simpson dio la probabilidad de que dos individuos cualesquiera extraídos al azar de
una comunidad infinitamente grande perteneciesen a diferentes especies como:
=
Donde es la proporción de individuos en al i-esima especie. A medida que D se
incrementa, la diversidad decrece, por lo tanto, el índice de Simpson es expresado
normalmente como 1-D o bien 1⁄ . Como critica a este índice es que esta recargado hacia
las especies más abundantes de la muestra mientras que es menos sensible a la riqueza de
especies.
c.5.- Índices de Berger-Parker
Este índice es fácilmente calculable. El índice de Berger Parker expresa la
importancia proporcional de las especies más abundantes.
⁄
=
Donde
= número de individuos de la especies más abundante. Al igual que
sucede con el índice de Simpson, generalmente se adopta el reciproco de modo que un
incremento en el valor del índice acompaña un incremento de la diversidad y una reducción
de la dominancia. Este índice es independiente de S pero está influenciado por el tamaño
muestral. A pesar de todo, es una de las medidas de diversidad más satisfactorias que se
encuentran disponibles.
7
Índices de Similitud
Es el sistema más fácil para medir la diversidad entre pares de localidades, en
especial son muy usados los índices de Jaccard y de Sorenson:
c6.- Medida de similaridad de Jaccard
C j  j / a  b  j 
Donde j = número de especies comunes en ambas localidades
a = número de especies en la localidad A
b = número de especies en la localidad B
c7.- Medida de similaridad de Sorenson (datos cualitativos)
C s  2 j / a  b 
Esos índices están diseñados para ser igual a 1 en casos de similaridad completa, e
igual a 0 si las estaciones son diferentes. Una de las grandes ventajas es su simplicidad. Un
inconveniente es que estos índices no consideran la abundancia de especies. Todas las
especies tienen un peso igual en la ecuación, con independencias si son abundantes o raras.
Esta consideración ha conducido a que las medidas de similaridad se basen en datos
cuantitativos:
c8.- Medida de similaridad de Sorenson (datos cuantitativos)
C N 2 jN / aN  bN 
Donde aN = número de individuos de la localidad A
bN = número de individuos de la localidad B
jN = suma de las abundancias de especies que presenta abundancia inferior. Así, si
se han hallado 12 individuos de una especie en la localidad A y 20 individuos de la misma
especie en la localidad B, el valor 12 será el incluido en la sumatoria para obtener el jN .
Sin embargo, se ha investigado diversos índices cuantitativos de similaridad y se ha
hallado que todos estaban fuertemente influenciados por la riqueza de especies y el tamaño
muestral, con excepción de uno:
8
c9.- Medida Morisita-Horn
C MH 
2 an i *bn i 
da  dbaN * bn
Donde aN = número de individuos en la localidad A
bN = número de individuos en la localidad B
an i = número de individuos de la i-esima especie en la localidad B
bn i = número de individuos de la i-esima especie en la localidad B
 an
da 
aN 2
2
i
 bn
y db 
2
i
bN 2
Sin embargo, una desventaja de este índice es que está fuertemente influenciado por
la abundancia de la especie más común.
METODOS ESTADÍSTICOS Y PAQUETES INFORMÁTICOS
Los índices que se han mencionado en el apartado anterior pueden ser fácilmente
calculados gracias al software que actualmente se dispone y el cual en muchos casos es de
acceso libre y gratuito.
Dentro de estos paquetes de software se pueden nombrar:
BioDAP
Ecosim
Biodiversity
StatGraphics
XLSTAT
Epidat*
PRIMER-e
Luego, ya con un nivel de dificultad superior se encuentran disponibles programas
más avanzados como:
9
Proyecto R
WinBUGS*
*Programas estadísticos con módulos o exclusivamente bayesianos.
La estadística que la mayoría de nosotros usa habitualmente recibe
como
denominación “frecuentista” o “clásica”, esto es así debido a que existe otro tipo de
estadística, diferente a la que se enseña en nuestra facultad, y tiene mucho auge en el
mundo actualmente: La Estadística Bayesiana.
Este tipo de estadística nació (paradójicamente) con antelación a la estadística
clásica (o frecuentista). Poco se sabe de su creador salvo datos puntuales que no vienen al
caso.
Se basa en un teorema muy sencillo:
Distribución a Priori x verisimilitud α Distribución a Posteriori
Se leería así: “la distribución a Priori (lo que conocemos o sabemos) multiplicada por la
verosimilitud (la probabilidad puntual del hecho que observamos) es proporcional (o igual)
a una distribución a Posteriori.”
Sobre la estadística bayesiana:
La ecología es una ciencia naturalmente incierta, en la cual los datos arrojan
mensajes ambiguos. La aplicación de métodos estadísticos apropiados para el análisis y la
interpretación de los resultados es un desafío continuo, más teniendo en cuenta la crisis
actual de la teoría frecuentista.
Está de más decir que si se dispone de información previa fiable vale la pena
abordar los problemas ecológicos “a la bayesiana” ya que los resultados pueden diferir de
manera sustancial. En la práctica, se pueden abordar mediante estadística bayesiana tanto
los análisis más sencillos (medias, regresiones, correlaciones, análisis de la varianza,
análisis de proporciones) como los muy complejos (análisis de captura-recaptura, análisis
de variabilidad, series temporales, etc.) debido a que los modelos bayesianos son
extremadamente flexibles. También es posible corregir la sobredispersión y la
pseudoreplicación (Martinez et al 2008).
10
A modo de resumen, y tomando como base el trabajo de Ellison (2004) podemos
decir que la estadística bayesiana difiere de la estadística clásica en lo siguiente:
1- La inferencia frecuentista estima la probabilidad de los datos ocurriendo a partir
de una hipótesis particular, mientras la estadística bayesiana da una medida cuantitativa de
la probabilidad de que la hipótesis planteada sea verdad a partir de los datos disponibles.
2- Las definiciones de probabilidad son muy diferentes, mientras los “frecuentistas”
definen probabilidad en términos de muestreos a largo tiempo (infinitos) relativo a la
frecuencia de los eventos, los “bayesianos” definen la probabilidad como un grado
individual de creencia en la verosimilitud de un evento. Dicho de otra forma en la
estadística frecuentista los p-values representan la “probabilidad” de generar una base de
datos igual a los valores más extremos que los observados (Basañez et al 2004). La
estadística bayesiana valora la credibilidad o verosimilitud de las hipótesis en lugar de
obligarnos a adoptar decisiones dicotómicas sobre ellas, de manera que nos permite “poner
al día” la opinión que una hipótesis nos merece a la luz de nuevos datos (Silva & Benavides
2001). Los bayesianos, expresan el “grado de credibilidad” en los posibles valores que el
parámetro puede tomar en la forma de una distribución de probabilidad. Debe tenerse en
cuenta que a medida que el tamaño muestreal se incrementa, la inferencia se ve más
influenciada por los datos que por la información previa (Basañez et al 2004), con lo cual,
si se dispone de un N muy grande, la estadística frecuentista y bayesiana tenderán a valores
similares.
3- La inferencia bayesiana usa el conocimiento a prior junto con los datos de la
muestra, mientras la inferencia frecuentista usa solo la información de los datos. Lejos de
operar en un vacío total de información el modelo de análisis bayesiano exige contemplar
formal y explícitamente el conocimiento previo (Silva & Benavides 2001).
4-los frecuentistas consideran a los parámetros fijos y desconocidos mientras la
muestra se considera tomada al azar y cada vez que el experimento se repite los datos
tomados del campo son considerados como un conjunto diferente. En contraste la
inferencia bayesiana trata a los parámetros del modelo como variables al azar mientras que
la muestra es considerada fija. Esto significa que la inferencia acerca de los parámetros se
hace condicional a partir de los datos conocidos que representan lo que se observa en ese
momento y suponiendo que tal vez, el experimento no podría ser repetido (Basañez et al
2004).
5- La estadística Bayesiana no arrastra el problema planteado por el tamaño
muestreal en el sentido de que, si esta es pequeño, el impacto informativo también lo será,
pero si ocurre lo contrario, más adecuadamente se podrá valorar la realidad que esa muestra
representa (Silva & Benavides 2001).
Se ha discutido y argumentado que la aproximación bayesiana es más entendible y
de fácil utilización que la teoría clásica. Los estadísticos bayesianos directamente pueden
responder las interrogantes generados por los usuarios, preguntas como por ejemplo “como
modifican estos datos mis conocimientos previos? Como afectan mis planes y acciones?, en
una forma que la estadística clásica no lo hace (ni puede). Y como dice Jackson (1976)
11
acerca del teorema de Bayes “es el análogo matemático, o incluso la formulación
matemática del proceso de aprender gracias a la experiencia”
Bibliografía citada:

Basañez M.G., Marshall C., Carabin H., Gyorkos T. & Joseph L. 2004. Bayesian
statistics for parasitologists. Trends in Parasitology, 20(2):85-91.

Ellison A.M. 2004. Bayesian inference in ecology. Ecology Letters 7:509-520.

Jackson P. H. 1976 "The philosophy and methodology of Bayesian inference" pp.
3-16 in D.N.M. de Gruijter and L.J. Th. vanderKamp (eds.) Advances in
Psychological and Educational Measurement. London: John Wiley.

Magurran A. E. 1988. Ecological diversity and its measurements. Princeton
University Press, Princeton, 179 págs.

Martinez A. A., Conesa D. & Oro D.2008. Herramientas estadísticas para resolver
contrastes de hipotesis con contenido biologico: su uso en ecología del siglo XXI.
Acta Zoologica Mexicana (nueva serie) 24(2):201-220.

Silva L.C. & Benavides A. 2001.El enfoque bayesiano: otra manera de inferior.
Gaceta Sanitaria, 15(4):341-346.
12