Ejercicios de Transformadas de Laplace

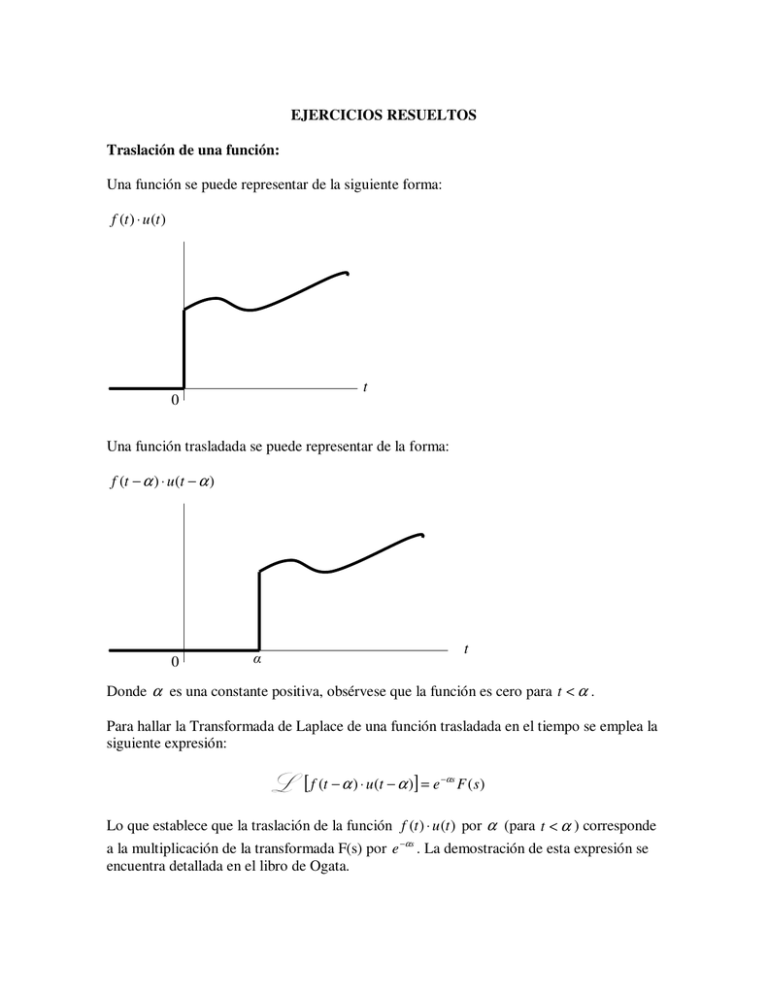
EJERCICIOS RESUELTOS
Traslación de una función:
Una función se puede representar de la siguiente forma:
f (t ) ⋅ u (t )
t
0
Una función trasladada se puede representar de la forma:
f (t − α ) ⋅ u (t − α )
0
t
α
Donde α es una constante positiva, obsérvese que la función es cero para t < α .
Para hallar la Transformada de Laplace de una función trasladada en el tiempo se emplea la
siguiente expresión:
L
[ f (t − α ) ⋅ u(t − α )] = e −αs F ( s)
Lo que establece que la traslación de la función f (t ) ⋅ u (t ) por α (para t < α ) corresponde
a la multiplicación de la transformada F(s) por e −αs . La demostración de esta expresión se
encuentra detallada en el libro de Ogata.
Ejemplo:
Hallar la Transformada de Laplace de la función f (t ) mostrada:
1
0
a
t
2a
-1
Esta función se puede ver como una suma de varias funciones:
1. Una función escalón unitario hasta el valor de a: u (t )
2. Para que la función decaiga al valor de -1 en a se le debe sumar un escalón de
tamaño -2 trasladado en a: − 2u (t − a )
3. Para que la función suba a cero en 2a se debe sumar otro escalón unitario trasladado
en 2a: u (t − 2a)
Entonces, la función se puede definir como:
f (t ) = u (t ) − 2u (t − a ) + u (t − 2a )
Entonces, aplicando la propiedad de la Transformada de Laplace de una función trasladada
se tiene la respuesta siguiente:
L
L
L
[u(t )] = 1
s
[− 2u (t − a)] = −2 1 e −as
s
1 − 2 as
[u(t − 2a)] = e
s
F ( s) =
1
1
1
− 2 e − as + e − 2 as
s
s
s
Gráficamente:
u (t )
1
0
a
2a
a
2a
a
2a
t
− 2u (t − a )
0
t
-2
u (t − 2 a )
1
0
t
La suma de estas tres funciones da como resultado la función original:
f (t ) = u (t ) − 2u (t − a ) + u (t − 2a )
La Transformada de Laplace de esta función también puede calcularse utilizando la fórmula
de la Integral de Laplace:
∞
a
2a
∞
0
a
2a
F ( s ) = ∫ f (t )e − st dt = ∫ (1)e − st dt + ∫ (−1)e − st dt + ∫ (0)e − st dt
0
a
2a
F ( s ) = ∫ e − st dt − ∫ e − st dt
0
a
Otro ejemplo donde se emplean otras propiedades de la Transformada de Laplace:
1. Hallar la transformada de Laplace de la siguiente función:
0


f (t ) = 
t 2 sen( wt )

t<0
t≥0
Sabiendo por tabla que:
L
sen( wt ) =
w
s + w2
2
Y aplicando el teorema de diferenciación compleja (ver tabla de propiedades de la
Transformada de Laplace):
L [t
2
d 2 F ( s)
f (t ) =
ds 2
]
Entonces, la Transformada de Laplace de la función es la segunda deriva de la
Transformada de Laplace del sen(wt):
L [t sen(wt )] = d
ds
2
2
2
 w 
 2
2 
s +w 
'
− 2 ws
 w 
=
 2
2 
s +w 
s2 + w2
(
 − 2 ws

 s2 + w2

(
'
)
2
 − 2 w s 2 + w 2 2 + 2 ws ⋅ 2 s 2 + w 2 2 s − 2w s 2 + w 2 2 + 8ws 2 s 2 + w 2
 =
=
2 
4
2
2 4
s
+
w
s 2 + w2

− 2w s 2 + w 2 + 8ws 2 − 2 ws 2 − 2w 3 + 8ws 2 − 2 w 3 + 6 ws 2
=
=
=
3
3
3
s 2 + w2
s2 + w2
s 2 + w2
(
)
(
(
)
(
)
)
(
)
(
)
(
)
)
(
(
)
(
)
)
Recomendaciones: Por favor revisar los ejercicios resueltos y propuestos en el libro de
Ogata, también revisar la Tabla de Propiedades de la Transformada de Laplace ya que
existen muchas otras propiedades que pudieran ayudar en el cálculo de la Transformada de
Laplace de una determinada función.
Ejercicio de Transformada Inversa de Laplace: Caso cuando la función posee un par de
polo imaginarios conjugados.
Hallar la Transformada Inversa de Laplace de:
F ( s) =
s+3
s + 2s + 5
2
Lo primero que se debe hacer es factorizar el denominador de la función F(s), en este caso
no se puede factorizar porque los polos son imaginarios y conjugados, lo mas conveniente
en este caso es expresar la función F(s) como una suma de funciones seno y coseno
amortiguados:
Por tabla, las funciones seno y coseno amortiguados son las siguientes:
L [e
L [e
w
(s + α ) 2 + w 2
s +α
−αt
cos(wt ) =
(s + α ) 2 + w2
−αt
]
sen (wt ) =
]
Lo primero, se trata de completar un trinomio cuadrado perfecto a 2 + 2ab + b 2 = (a + b )
en el denominador de la función F(s):
F ( s) =
2
s+3
s+3
s +3
=
=
2
s + 2 s + 1 + 4 ( s + 1) + 4 ( s + 1) 2 + 2 2
2
Ahora, observando esta última expresión, se puede concluir que proviene de un seno o un
coseno amortiguado, se reescribe a conveniencia nuevamente F(s):
F ( s) =
s +1+ 2
s +1
2
=
+
2
2
2
2
(s + 1) + 2
( s + 1) + 2
(s + 1) 2 + 2 2
Y en este caso se observa que una des fracciones resultantes es un seno amortiguado y la
otra fracción es un coseno amortiguado; por lo tanto, la Transformada Inversa de Laplace
de la función F(s) es:
f (t ) = e − t cos(2t ) + e −t sen(2t )
Recomendaciones: En el libro de Ogata aparecen ejemplos y ejercicios resueltos de este
caso, por favor revisar.