4.8. Ejercicios

Teorı́a de la Comunicación
4.8.
Ejercicios
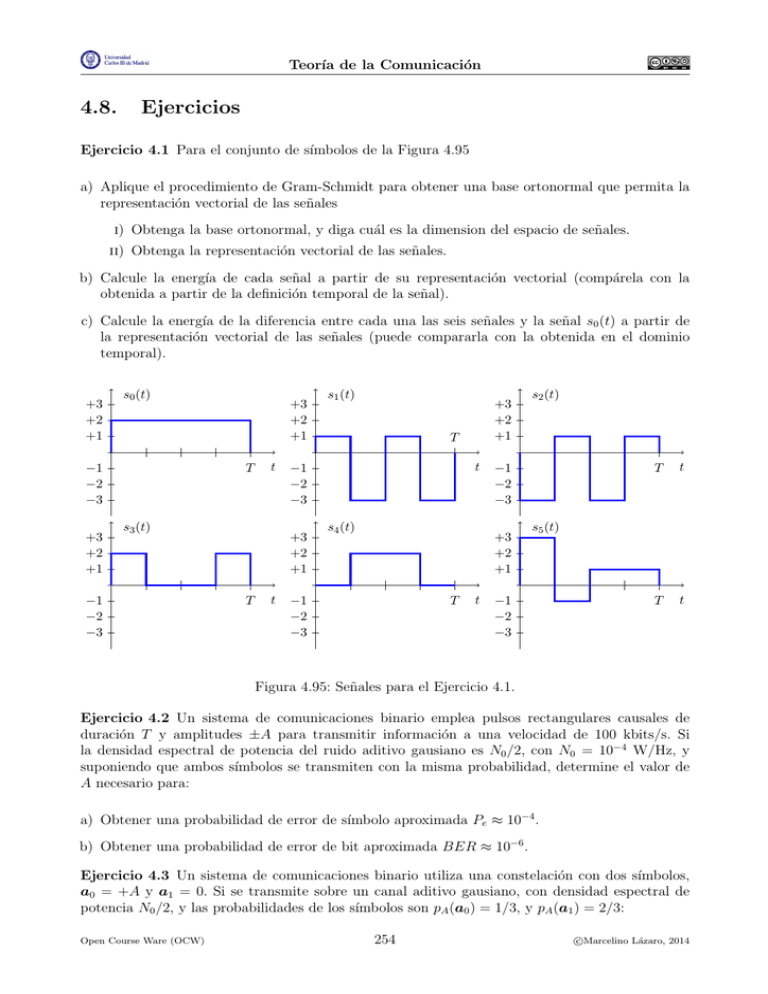
Ejercicio 4.1 Para el conjunto de sı́mbolos de la Figura 4.95
a) Aplique el procedimiento de Gram-Schmidt para obtener una base ortonormal que permita la
representación vectorial de las señales
i) Obtenga la base ortonormal, y diga cuál es la dimension del espacio de señales.
ii) Obtenga la representación vectorial de las señales.
b) Calcule la energı́a de cada señal a partir de su representación vectorial (compárela con la
obtenida a partir de la definición temporal de la señal).
c) Calcule la energı́a de la diferencia entre cada una las seis señales y la señal s0 (t) a partir de
la representación vectorial de las señales (puede compararla con la obtenida en el dominio
temporal).
+3
+2
+1
s0 (t)
T
1
2
3
+3
+2
+1
+3
+2
+1
t
s3 (t)
1
2
3
t
+3
+2
+1
T
t
1
2
3
+3
+2
+1
T
s1 (t)
s4 (t)
1
2
3
+3
+2
+1
T
1
2
3
t
s2 (t)
T
t
T
t
s5 (t)
1
2
3
Figura 4.95: Señales para el Ejercicio 4.1.
Ejercicio 4.2 Un sistema de comunicaciones binario emplea pulsos rectangulares causales de
duración T y amplitudes ±A para transmitir información a una velocidad de 100 kbits/s. Si
la densidad espectral de potencia del ruido aditivo gausiano es N0 /2, con N0 = 10 4 W/Hz, y
suponiendo que ambos sı́mbolos se transmiten con la misma probabilidad, determine el valor de
A necesario para:
a) Obtener una probabilidad de error de sı́mbolo aproximada Pe ⇡ 10 4 .
b) Obtener una probabilidad de error de bit aproximada BER ⇡ 10 6 .
Ejercicio 4.3 Un sistema de comunicaciones binario utiliza una constelación con dos sı́mbolos,
a0 = +A y a1 = 0. Si se transmite sobre un canal aditivo gausiano, con densidad espectral de
potencia N0 /2, y las probabilidades de los sı́mbolos son pA (a0 ) = 1/3, y pA (a1 ) = 2/3:
Open Course Ware (OCW)
254
c Marcelino Lázaro, 2014
Teorı́a de la Comunicación
a) Calcule el decisor óptimo (es decir, calcule el umbral de decisión).
b) Calcule la probabilidad de error.
Ejercicio 4.4 Se tiene la constelación de la Figura 4.96. Se supone que los sı́mbolos tienen la
misma probabilidad. Tomando T = 1
6
p
a0
T s
s a2
p
sa1 -
p
T
T
Figura 4.96: Constelación Ejercicio 4.4.
a) Calcule al energı́a media por sı́mbolo, Es .
b) Diseñe una constelación alternativa que, con la misma probabilidad de error, tenga la mı́nima
energı́a media por sı́mbolo. Calcule el nuevo valor de Es .
c) Para cualquiera de las dos constelaciones, obtenga un lı́mite de la probabilidad de error mediante la cota de la unión y la cota holgada.
Ejercicio 4.5 Para la implementación de un sistema de comunicaciones de tres sı́mbolos equiprobables, el modulador transmite las tres señales mostradas en la Figura 4.97.
a) Calcule la energı́a media por sı́mbolo.
b) Calcule alguna cota de la probabilidad de error.
Ejercicio 4.6 Un sistema de comunicaciones emplea la constelación unidimensional
a0 = 0, a1 = 1, a2 = 2, a3 = 3,
Las observaciones proporcionadas por el demodulador están caracterizadas por el canal discreto
equivalente
q[n] = A[n] + z[n],
donde cada muestra del término de ruido, z[n], tiene la función densidad de probabilidad representada en la Figura 4.98.
a) Obtenga la expresión analı́tica de la función densidad de probabilidad de la observación condicionada a la transmisión de cada sı́mbolo (es decir, fq|A (q|ai ), para todo i).
b) Diseñe el decisor óptimo para sı́mbolos equiprobables.
c) Calcule la probabilidad de error para el decisor anterior.
Open Course Ware (OCW)
255
c Marcelino Lázaro, 2014
Teorı́a de la Comunicación
6s0 (t)
6s1 (t)
.....
... .....
. ..
1
1
.. .....
.......
.......
.....
.......
.
.
.
.
.
.
.
... ...... ......
.. .....
.. ..... ..
.. .....
.
.
.
.
.
.
....
... ....
....
.... ..
....
..
...
...
.. ..
. - ....
..
....
...
...
.
.
....
.
.
.
.
1 ..... .... 2
3
1
2
3
......
1
1
2
2
2
2
2
6s2 (t)
1
...
.................................
....
...
..
..
.
.
...
2 ...
.3
.. 1
...
... ...
.
.
1 ... .
... .
... ..
... ..
... ..
... ..
..
..
2
Figura 4.97: Señales Ejercicio 4.5.
6
fz (z)
..
.... ........
.
.
.
.
.....
...
.....
....
.
.
.
.....
.
.
.
.
.....
...
.
.
.
.....
.
.
.
.
.....
.
....
.
-1
-
1
Figura 4.98: Constelación y función densidad de probabilidad del término de ruido para el Ejercicio
4.6.
Open Course Ware (OCW)
256
c Marcelino Lázaro, 2014
Teorı́a de la Comunicación
d) Diseñe el decisor óptimo para las siguientes probabilidades de sı́mbolo: pA (a0 ) = pA (a3 ) = 1/6,
pA (a1 ) = pA (a2 ) = 1/3.
e) Calcule la probabilidad de error para el decisor anterior.
Ejercicio 4.7 Un sistema de comunicaciones binario utiliza las siguientes señales para la transmisión de los dos sı́mbolos:
8s
>
< Eb
, 0tT
s0 (t) = s1 (t) =
.
N
0
>
:
0,
en otro caso
El receptor se implementa como se muestra en la Figura 4.99 (representación para la recepción
del primer sı́mbolo de la secuencia).
r(t) = si (t) + n(t)
Z
-
✓
q
t
0
·dt
-
Detector
-
?
t=T
Figura 4.99: Receptor para el Ejercicio 4.7.
Determine la relación señal a ruido a la salida del demodulador (en q), suponiendo que el ruido
aditivo es de media nula, gausiano y con densidad espectral de potencia N0 /2 W/Hz.
Ejercicio 4.8 El código de lı́nea de Mánchester utiliza las señales de la Figura 4.100 para transmitir los dos sı́mbolos del código.
a) Determine la probabilidad de error si ambos sı́mbolos se transmiten con igual probabilidad.
b) Determine la probabilidad de error si la probabilidad de los sı́mbolos es pA (a0 ) = p y pA (a1 ) =
1 p.
6
s (t)
6
s (t)
0
1
+A
+A
T
-
-
t
A
T
t
A
Figura 4.100: Señales para el Ejercicio 4.8.
Ejercicio 4.9 Considere un sistema digital de comunicaciones que transmite la información empleando una constelación QAM a una tasa de sı́mbolo de 2400 baudios (sı́mbolos/s). Se asume
ruido aditivo blanco y gausiano.
Open Course Ware (OCW)
257
c Marcelino Lázaro, 2014
Teorı́a de la Comunicación
a) Determine la relación Eb /N0 requerida para conseguir una probabilidad de error de sı́mbolo
aproximada de 10 5 para una tasa binaria de 4800 bits/s.
b) Repita el cálculo para una tasa binaria de 9600 bits/s.
c) Repita el cálculo para una tasa binaria de 19200 bits/s.
d) Exponga las conclusiones obtenidas a partir de estos resultados.
Ejercicio 4.10 Un sistema de comunicaciones transmite dos sı́mbolos mediante las señales s0 (t)
y s1 (t) que se muestran a continuación en la Figura 4.101
s0 (t)
s1 (t)
6
6
A
T /2
-
0
T /2
T
t
T
-
t
0
A
Figura 4.101: Señales para el Ejercicio 4.10.
a) Se tiene un canal aditivo gausiano (ruido blanco con densidad espectral de potencia N0 /2).
Dibuje la constelación, diseñe el receptor (demodulador + decisor) óptimo, y calcule la probabilidad de error.
b) Si el canal es tal que su salida a una entrada s(t) es ↵s(t) + ↵A, de nuevo con el mismo tipo
de ruido aditivo, rediseñe el decisor óptimo y calcule la probabilidad de error.
c) Si en la situación del apartado a) se utiliza el demodulador de la Figura 4.102, diseñe el decisor
óptimo y calcule la probabilidad de error en este caso. Comente los resultados comparándolos
con los obtenidos en el apartado a).
r(t) -
Rt
0
· dt
q0
?
t=T
Figura 4.102: Demodulador para el Ejercicio 4.10.
NOTA: Tenga en cuenta que si no se emplea un demodulador normalizado, la varianza de ruido
discreto ya no es N0 /2.
Ejercicio 4.11 Las cuatro señales de la Figura 4.103 se utilizan para transmitir 4 sı́mbolos igualmente probables en un sistema de comunicaciones. Se considera que dichas señales se transmiten
a través de un canal gausiano con densidad espectral de potencia N0 /2.
a) Diseñe el transmisor: codificador (constelación) y modulador ({ i (t)}, i = 0, 1, · · · , N ).
Open Course Ware (OCW)
258
c Marcelino Lázaro, 2014
Teorı́a de la Comunicación
6s0 (t)
6s1 (t)
A
A
-
1
-
t
2
1
6s2 (t)
t
2
6s3 (t)
2A
3
2A
3
A
3
A
3
-
1
-
t
2
1
t
2
Figura 4.103: Señales para el Ejercicio 4.11.
b) Calcule la energı́a media por sı́mbolo del sistema, y realice una asignación óptima de bits
a cada sı́mbolo justificando dicha asignación (sin la justificación adecuada, la asignación no
será valorada).
c) Diseñe el receptor óptimo (demodulador + decisor) utilizando filtros adaptados causales (hay
que proporcionar la expresión analı́tica o dibujarlos), obtenga las expresiones de la función
densidad de probabilidad de la observación a la salida del demodulador condicionada a la
transmisión de cada sı́mbolo (fq|A (q|ai ), i = 0, 1, 2, 3), y calcule la probabilidad de error.
d) Si se utiliza el demodulador de la Figura 4.104, diseñe el decisor óptimo, obtenga las expresiones
de la función densidad de probabilidad de la observación a la salida del demodulador condicionada a la transmisión de cada sı́mbolo (fq|A (q|ai ), i = 0, 1, 2, 3), y calcule la probabilidad
de error. Compare este valor con el obtenido en el apartado anterior y explique los resultados
obtenidos.
r(t)-✏
@
@
6
g(t)
1
-
RT
0
• dt
q
6
g(t)
-
-
1
1
2
t
Figura 4.104: Demodulador para el Ejercicio 4.11.
Ejercicio 4.12 Se tiene un sistema de comunicaciones con un transmisor con una tasa de sı́mbolo
Rs = 103 baudios. Se asume ruido aditivo blanco, gausiano, y densidad espectral de potencia N0 /2,
con N0 = 2 ⇥ 10 2 .
a) Una aproximación comúnmente empleada en sistemas de comunicaciones digitales para la proOpen Course Ware (OCW)
259
c Marcelino Lázaro, 2014
Teorı́a de la Comunicación
babilidad de error de sı́mbolo es
d
pmin
2 No /2
Pe ⇡ k · Q
!
,
(4.4)
donde dmin es la mı́nima distancia entre dos puntos de la constelación y k es el máximo número
de sı́mbolos que se encuentran a dmin de un sı́mbolo de la constelación.
i) Utilizando la aproximación (4.4), diseñe el codificador unidimensional óptimo del sistema
de comunicaciones, con la menor energı́a media por sı́mbolo, para obtener una probabilidad
de error de sı́mbolo aproximada Pe ⇡ 2 · 10 4 transmitiendo a una velocidad binaria
Rb = 2 ⇥ 103 bits/s.
ii) Realice una asignación óptima de bits a cada sı́mbolo, explicando la razón de dicha asignación, y calcule la tasa de error binaria aproximada.
b) Si el sistema de comunicaciones utiliza el codificador y el modulador definidos en la Figura
4.105:
q
3 T3
a0
q
s
s
a1
T
3
q
T
3
s
a2
3
q
q
T
3
s-
a3
3
T
6 0 (t)
@
@
@
@
@
@
-
t
T
Figura 4.105: Codificador y modulador para el Ejercicio 4.12.
i) Diseñe el demodulador óptimo utilizando un correlador y utilizando un filtro adaptado
causal (en este último caso proporcione la expresión analı́tica de la respuesta al impulso
del filtro o bien dibújela).
ii) Si por simplicidad, en lugar del demodulador óptimo se emplea un demodulador que
realiza la siguiente operación sobre la señal recibida (r(t))
q =2·
Z
T
r(t) dt,
0
diseñe el decisor óptimo y calcule la probabilidad de error de sı́mbolo asumiendo sı́mbolos
equiprobables. Discuta si esta probabilidad de error será mayor o menor que la obtenida
con el demodulador del apartado anterior.
Ejercicio 4.13 Se va a diseñar un sistema de comunicaciones que utilizará las ocho señales de la
Figura 4.106 para transmitir ocho sı́mbolos con igual probabilidad. El canal únicamente introduce
ruido, que se considerará blanco, gausiano, estacionario y con densidad espectral de potencia N0 /2.
Por simplicidad en los cálculos, considere T = 2.
a) Realice la asignación de los bits que transporta cada una de las señales para obtener la mı́nima
probabilidad de error de bit, y justifique la razón para elegir dicha asignación.
Open Course Ware (OCW)
260
c Marcelino Lázaro, 2014
Teorı́a de la Comunicación
2
1
s0 (t)
6
1
2
2
1
T
T
2
2
1
t
1
2
T
2
1
t
T
T
2
1
2
s4 (t)
6
T
2
s1 (t)
6
t
s5 (t)
6
T
2
1
2
T
t
2
1
s2 (t)
6
T
2
1
2
2
1
T
2
1
t
1
2
T
T
2
1
2
s6 (t)
6
T
2
s3 (t)
6
2
1
t
T
t
T
t
s7 (t)
6
T
2
1
2
Figura 4.106: Señales para el Ejercicio 4.13.
b) Obtenga otras 8 señales alternativas (dibuje las ocho señales o proporcione sus expresiones
analı́ticas) con las que se pueda obtener la misma probabilidad de error que con el conjunto
original, pero que requieran una mı́nima energı́a media por sı́mbolo, y calcule esa energı́a media
por sı́mbolo mı́nima.
c) Diseñe el receptor óptimo (demodulador + decisor), y calcule la probabilidad de error obtenida
(puede hacerlo utilizando tanto el conjunto original de señales como el obtenido en la sección
b), ya que en ambos casos la probabilidad de error ha de ser la misma).
Ejercicio 4.14 Un sistema de comunicaciones utiliza una constelación formada por los siguientes
4 sı́mbolos,




a0 =
+1
+1
1
+1
, a1 =
, a2 =
1
1
, a3 =
+1
1
,
que se transmiten con igual probabilidad, y un modulador dado por las funciones base de la Figura
4.107.
0 (t)
1 (t)
p1
T
6
p1
T
6
T
p1
T
T
t
p1
T
t
Figura 4.107: Demodulador para el Ejercicio 4.14.
Por simplicidad en los cálculos, en lo sucesivo considere T = 1. Considere también la transmisión
sobre un canal gausiano con densidad espectral de potencia de ruido blanco N0 /2.
a) Realice la asignación binaria que minimiza la probabilidad de error de bit, justificando dicha
asignación (sin la justificación adecuada, la asignación no será valorada), y calcule la velocidad
de transmisión de sı́mbolos, Rs , y la velocidad de transmisión binaria, Rb .
b) Represente las cuatro señales utilizadas para la transmisión de cada sı́mbolo, si (t), i = {0, 1, 2, 3},
y la señal resultante de la transmisión de la siguiente secuencia de sı́mbolos
A[0] = a1 , A[1] = a0 , A[2] = a3 , A[3] = a0 , A[4] = a2 .
Open Course Ware (OCW)
261
c Marcelino Lázaro, 2014
Teorı́a de la Comunicación
c) Diseñe el receptor óptimo (demodulador + decisor), y calcule la probabilidad de error obtenida
con este receptor.
d) Si en lugar del demodulador óptimo se utiliza el demodulador de la Figura 4.108, diseñe el
decisor óptimo para ese demodulador y calcule la probabilidad de error resultante.
- 2·
Z
T /2
-
• dt
0
?
✏
r(t)
-
q
-
6
-
Z
T
T /2
-
• dt
Figura 4.108: Demodulador para el Ejercicio 4.14.
Ejercicio 4.15 Un sistema digital de comunicaciones usa una constelación de 8 sı́mbolos equiprobables como la que se muestra en la figura. Se supone que el ruido asociado a la transmisión se
modela como un proceso de ruido térmico habitual, estacionario, blanco, gausiano y con densidad
espectral de potencia Sn (j!) = N20 , siendo N0 = 0,03 para este caso.
a2
....................
a3..........................................u
...........
........
a4
u
ua1
.......
...
.....
......
....
....
....
....
...
...
...
...
.
...
..
.
...
....
...
...
..
..
...
.
..
..
..
..
...
....
...
.
...
.
...
..
..
...
...
....
....
....
...
.....
.
.
.
.
......
.
........
......
.......
..........
...................... ...............................
....
u
u
a5
R -u
a0
u
a6
u
a7
a) Si se desea que la probabilidad de error de sı́mbolo sea aproximadamente Pe ⇡ 2 ⇥ 10 6 :
i) determine el valor del radio R requerido;
ii) calcule la energı́a media por sı́mbolo, Es , de la constelación resultante;
iii) realice la asignación binaria óptima justificándola (sin justificación no se considerará válida), y estime la tasa de error de bit (BER) aproximada usando dicha asignación si se
asume que la relación señal a ruido es alta.
b) Si se desea transmitir a una tasa binaria Rb = 1500 bits por segundo a través de un canal en
banda base (inicialmente sin limitación en el ancho de banda):
i) elija una base ortonormal apropiada para la transmisión justificando su elección (debe
proporcionar las expresiones analı́ticas de cada elemento de la base o un dibujo de la
misma, pero en cualquier caso han de estar claramente indicados los valores numéricos de
amplitudes y duración de las señales, T seg.);
Open Course Ware (OCW)
262
c Marcelino Lázaro, 2014
Teorı́a de la Comunicación
ii) diseñe un demodulador óptimo para el sistema de comunicaciones.
c) En cuanto al decisor
i) diseñe el decisor óptimo para el sistema;
ii) calcule la cota de la unión (sin despreciar ningún término ni hacer ninguna aproximación);
iii) obtenga la cota holgada y escriba la cota resultante para la probabilidad de error en
Es
función del cociente o relación N
.
0
NOTA: la distancia entre dos puntos de una circunferencia de radio R está dada por d =
2R sen 2✓ , donde ✓ es el ángulo que forman los radios que unen dichos puntos con el centro.
Ejercicio 4.16 Un sistema de comunicaciones utiliza una constelación formada por los siguientes
4 sı́mbolos,




a0 =
0
0
, a1 =
0
1
1
0
, a2 =
1
1
, a3 =
,
que se transmiten con igual probabilidad, y un modulador dado por las funciones base de la figura
6
+A
A
0 (t)
...
...
...
...
...
...
..
6
1 (t)
+B
...
...
...
..
-
T
t
+ B2
B
2
B
...
...
...
...
.
..
..
..
..
..
..
.
...
...
...
...
...
...
...
...
..
...
...
...
...
.
-
T
t
Por simplicidad en los cálculos, en lo sucesivo considere T = 1. Considere también la transmisión
sobre un canal gausiano con densidad espectral de potencia de ruido blanco N0 /2.
a) Determine los valores de A y B, demuestre que las funciones forman una base ortonormal, y
calcule la velocidad de transmisión o tasa de sı́mbolo y la velocidad de transmisión o tasa de
bit.
b) Represente las señales si (t) asociadas a la transmisión de cada sı́mbolo ai , y el fragmento de
la señal resultante de la transmisión de los siguientes primeros 5 sı́mbolos de la secuencia
A[0] = a1 , A[1] = a0 , A[2] = a3 , A[3] = a0 , A[4] = a2 .
c) Realice la asignación binaria para cada sı́mbolo, justificando dicha asignación (sin esta justificación no se considerará la asignación como válida), y calcule la energı́a media por sı́mbolo
del sistema. ¿Es la constelación utilizada la más apropiada en términos del compromiso entre
uso de energı́a y prestaciones (explique claramente por qué sı́ o por qué no)?
d) Diseñe el demodulador óptimo, el decisor óptimo, y calcule la probabilidad de error de sı́mbolo
exacta del sistema.
e) Obtenga la aproximación de la probabilidad de error de sı́mbolo y acote dicha probabilidad de
error mediante la cota de la unión y mediante la cota holgada.
Open Course Ware (OCW)
263
c Marcelino Lázaro, 2014