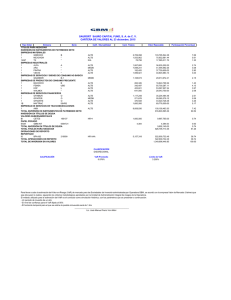
α =σ σ σ

ECONOMETRIA II ADE LADE-DERECHO. CURSO 2007/2008
Hoja de ejercicios 4
PARTE A)
Marque con una X la respuesta o respuestas correctas
A.1. Se ha estimado el siguiente modelo VAR
y1t = 0,5 y1t-1 + 0,2y2t-1 +ε1t
y2t =
0,8y2t-1 +ε2t
Donde: ε1t y ε2t son procesos ruido blanco con:
 0, 4 −0, 02 
Var(ε)= 

 −0, 02 0, 3 
Señale cuales de las siguientes afirmaciones son ciertas
(a) El modelo se caracteriza por tener solamente causalidad unidireccional
de y1t a y2t.
(b) Las variables y1t-1 y y2t-1 son predeterminadas
(c) Existe correlación contemporánea entre los procesos del modelo
(d) El sistema es estable
(e) El modelo no es recursivo
(f) Las variables y1t-1 y y2t-1 son endógenas
A.2. Considere el siguiente modelo de mecanismo de corrección del equilibrio
(mecanismo de corrección del error) entre dos variables I(1), Yt y X t :
∆Yt = 0.1 + α 1 (Yt −1 − 0.3 − 2 X t −1 ) + a1t
(1)
∆X t = 0.13 + a 2t
donde a1t y a 2t son ruidos blancos con σ 11 = σ 22 = 1 y σ 12 = 0 .
Señale cuáles de las siguientes afirmaciones son correctas:
(a) Existe una relación de equilibrio en el largo plazo entre Yt y X t , que
viene dada por Yt = 0.3 + 2 X t .
(b) X t es débilmente exógena en la ecuación de Yt .
(c) Las variables no están cointegradas.
(d) El coeficiente α 1 puede ser mayor o igual que cero.
(e) Las variables están cointegradas pero no comparten tendencia común.
PARTE B
B.1. Dados los siguientes modelos de función de transferencia:
Yt = (2 – 3L2)Xt +Nt
a)
b) Yt =
c)
donde
1
X t +Nt
1 − 0,5 L
Yt =
N
t
υ
Xt -2 +Nt
1 − δL
es un proceso estacionario y
L es el operador de retardos.
Interprete estos modelos y cuantifique en cada uno de ellos la respuesta a un
aumento unitario
en la variable Xt,. de tipo impulso, para los primeros 4
retardos, y también la ganancia de cada uno de ellos.
B.2 Un economista estima un modelo VAR para analizar las relaciones
dinámicas entre la inflación y el logaritmo del consumo privado (LCON) para
un determinada economía utilizando datos anuales. Como no conoce el orden
del modelo VAR estima tres modelos alternativos Var(1), Var(2) y Var(3). Con
la información proporcionada en los cuadros 1 y 2, responda a las siguientes
preguntas:
a) Decida cual es el orden más adecuado de dicho modelo
b).¿Cuál es el número de restricciones que comporta el paso del modelo
VAR(3) al VAR(2) y del VAR(2) al VAR(1)?
c) Diga cual es la relación de causalidad entre la inflación y LCON
d) A la vista de estos resultados del apartado c cree que el economista utilizó
el tipo de modelización adecuada. Razone la respuesta.
Cuadro 1
Estadísticos de los modelos VAR sobre la inflación y el consumo privado
Longitud
del
retardo
(q)
1
Logaritmo de la
Verosimilitud
(logL)
Criterio de
AKAIKE
(AIC)
Criterio de
Schwarz
(SC)
-116,14
0,3921
0,4348
2
-81,829
0,2953
0,2973
3
-78,321
0,4348
0,3665
Nota: estimaciones Eviews
Cuadro 2
Pairwise Granger Causality Tests
Date: 05/18/08 Time: 18:04
Sample: 1960 1995
Lags: 2
Null Hypothesis:
LCONSUMO does not Granger Cause INFLA
INFLA does not Granger Cause LCONSUMO
Obs
F-Statistic
Probability
33
4.78677
3.45685
0.01629
0.04553
B.5 . Se intenta analizar la relación existente entre los precios mundiales del
mercado del cacao (pcacao) y los del mercado de café (pcafe). Utilizando la
información que se proporciona en los cuadros adjuntos, obtenidos de la
aplicación de eviews a las series anteriores en logaritmos (LPCACAO,
LPCAFE) para el periodo muestral 1960:01 2002:09 responda a las siguientes
preguntas justificando las respuestas:
(a) Verifique si las series son estacionarias y si no lo son determine el orden
de integración de ambas variables (cuadro1).
(b) A la luz de los resultados anteriores investigue la posible existencia de
alguna relación de cointegración entre ambas variables. A este respecto
se ha llevado a cabo el procedimiento en dos etapas de Engle-Granger
cuyos resultados se muestran en el cuadro 2.
(c) Exprese el modelo VEC estimado en el cuadro 3 en forma matricial ¿Es
correcta esta formulación del modelo a la vista de los resultados del
apartado anterior?
(d) Interprete los resultados del modelo VEC (corrección del error),
determinando cual es la relación de equilibrio o de largo plazo, el
coeficiente de ajuste de cada variable, etc. Verifique si alguna de las dos
variables es débilmente exógena en la ecuación de la otra.
Material auxiliar obtenido de Eviews
Cuadro 1. Test ADF de las variables
Variable LPCACAO
Null Hypothesis: LPCACAO has a unit root
Exogenous: Constant
Lag Length: 2 (Automatic based on SIC, MAXLAG=18)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
*MacKinnon (1996) one-sided p-values.
t-Statistic
Prob.*
-1.608590
-3.442945
-2.866988
-2.569733
0.4774
Variable D(LPCACAO)
Null Hypothesis: D(LPCACAO) has a unit root
Exogenous: Constant
Lag Length: 1 (Automatic based on SIC, MAXLAG=18)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
Prob.*
-14.79724
-3.442945
-2.866988
-2.569733
0.0000
*MacKinnon (1996) one-sided p-values.
Variable LPCAFE
Null Hypothesis: LPCAFE has a unit root
Exogenous: Constant
Lag Length: 1 (Automatic based on SIC, MAXLAG=18)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
Prob.*
-1.922600
-3.442919
-2.866976
-2.569727
0.3218
*MacKinnon (1996) one-sided p-values.
Variable D(DLPCAFE)
Null Hypothesis: D(LPCAFE) has a unit root
Exogenous: Constant
Lag Length: 0 (Automatic based on SIC, MAXLAG=18)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
*MacKinnon (1996) one-sided p-values.
t-Statistic
Prob.*
-16.64536
-3.442919
-2.866976
-2.569727
0.0000
Cuadro2. Procedimiento de cointegración de Engle-Granger
Estimación de la ecuación 1: LPCACAOt = c + β LPCAFEt +εεt
Dependent Variable: LPCACAO
Method: Least Squares
Date: 05/20/08 Time: 17:27
Sample: 1960M01 2002M09
Included observations: 513
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
LPCAFE
0.136019
0.897914
0.089273
0.020590
1.523628
43.60908
0.1282
0.0000
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.788209
0.787794
0.277915
39.46789
-70.04726
0.090501
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob(F-statistic)
3.992180
0.603299
0.280886
0.297417
1901.752
0.000000
TEST ADF DE LA VARIABLE RES1 (Residuos de la ecuación 1)
Null Hypothesis: RES1 has a unit root
Exogenous: None
Lag Length: 1 (Automatic based on SIC, MAXLAG=18)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
*MacKinnon (1996) one-sided p-values.
t-Statistic
Prob.*
-3.767162
-2.569495
-1.941444
-1.616283
0.0002
Cuadro3. Estimación modelo VEC
Vector Error Correction Estimates
Sample (adjusted): 1960M04 2002M09
Included observations: 510 after adjustments
Standard errors in ( ) & t-statistics in [ ]
Cointegrating Eq:
CointEq1
LPCACAO(-1)
LPCAFE(-1)
C
1.000000
-1.119561
(0.13088)
[-8.55428]
0.819018
Error Correction:
D(LPCACAO)
D(LPCAFE)
CointEq1
-0.009794
(0.00957)
[-1.02381]
0.033877
(0.00985)
[ 3.44011]
D(LPCACAO(-1))
0.349056
(0.04459)
[ 7.82749]
0.021640
(0.04591)
[ 0.47139]
D(LPCACAO(-2))
-0.121036
(0.04499)
[-2.69018]
0.023538
(0.04632)
[ 0.50820]
D(LPCAFE(-1))
0.025045
(0.04323)
[ 0.57938]
0.279703
(0.04450)
[ 6.28541]
D(LPCAFE(-2))
0.072563
(0.04368)
[ 1.66125]
0.091256
(0.04497)
[ 2.02944]
C
0.001998
(0.00277)
[ 0.72131]
0.000394
(0.00285)
[ 0.13825]
R-squared
Adj. R-squared
Sum sq. resids
S.E. equation
Akaike AIC
Schwarz SC
0.122065
0.113355
1.969152
0.062506
-2.695401
-2.645585
0.115301
0.106524
2.086831
0.064347
-2.637358
-2.587541