medición del riesgo de mercado bajo condiciones propicias para la

MEDICIÓN DEL RIESGO DE MERCADO
BAJO CONDICIONES PROPICIAS PARA
LA DISTORSIÓN DE LOS PRECIOS
20 de Febrero 2009
Contenido
Introducción General
1
2
1
Preliminares
1.1 Conceptos Básicos de Probabilidad . . . . . . . .
1.2 Medidas de Riesgo . . . . . . . . . . . . . . . . .
1.3 Los Conceptos de VaR y CVaR . . . . . . . . . .
1.4 Derivada del VaR y CVaR . . . . . . . . . . . . .
1.5 El VaR y CVaR de una distribución normal . . .
1.6 El VaR y CVaR de una distribución t no central
1.7 Teoría de Valores Extremos . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
5
7
9
14
15
19
21
Factores de Ajuste de la Volatilidad
2.1 Introducción . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Formulación Matemática . . . . . . . . . . . . . . . . . . .
2.3 Propiedades . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3.1 Caso Normal . . . . . . . . . . . . . . . . . . . . .
2.3.2 No Negatividad . . . . . . . . . . . . . . . . . . . .
2.3.3 F ∗ y El Nivel de Aversión al Riesgo δ . . . . . . .
2.3.4 F ∗ y el Nivel de Confianza α . . . . . . . . . . . .
2.4 Aplicaciones . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4.1 Bono M Diciembre 2007 . . . . . . . . . . . . . . .
2.4.2 Bono M Junio 2011 . . . . . . . . . . . . . . . . . .
2.5 Descomposición del Efecto de Distorsión . . . . . . . . .
2.5.1 Bono M Diciembre 2024 . . . . . . . . . . . . . . .
2.5.2 Factor de Distorsión del bono M Diciembre 2007
2.6 Otras variables de referencia . . . . . . . . . . . . . . . .
2.7 Aplicación de la Teoría de Valores Extremos . . . . . . .
2.7.1 Dificultades en la estimación del VaR y CVaR . .
2.7.2 Estimadores del VaR y CVaR usando TVE . . . .
2.7.3 Aplicación en la determinación de F ∗ . . . . . . .
2.8 Conclusiones . . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
23
23
23
25
25
26
28
31
32
33
34
35
36
36
36
38
38
40
41
43
i
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
Aplicación de Distribuciones Híbridas
3.1 Introducción y Motivación . . . . . . . . .
3.2 Distribuciones Híbridas . . . . . . . . . .
3.3 Formulación Matemática . . . . . . . . . .
H ( β)
H ( β)
3.4 Propiedades del VaRα , CVaRα
y β∗
3.4.1 Propiedades Básicas . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
H ( β)
3.5
3.6
3.7
3.8
3.9
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
H ( β)
3.4.2 Monotonicidad y Continuidad del VaRα
y CVaRα
3.4.3 Existencia y algunas propiedades de β∗ . . . . . . . . .
Determinación de la probabilidad óptima β∗ . . . . . . . . . . .
3.5.1 Determinación de la Distribución Híbrida . . . . . . . .
Caso Gaussiano-Gaussiano . . . . . . . . . . . . . . . . . . . . .
3.6.1 Solución utilizando simulación . . . . . . . . . . . . . . .
3.6.2 Solución mediante integración numérica . . . . . . . . .
Caso Gaussiano-t . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.7.1 Solución utilizando simulación . . . . . . . . . . . . . . .
3.7.2 Solución mediante integración numérica . . . . . . . . .
3.7.3 Comparación entre el modelo Gaussiano-Gaussiano y el
Gaussiano-t . . . . . . . . . . . . . . . . . . . . . . . . . .
Comparación de β∗ con el factor de ajuste F ∗ . . . . . . . . . .
Conclusiones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Conclusiones Generales
46
46
47
51
52
53
54
59
60
63
64
65
66
71
71
72
77
78
81
83
A Convexidad y Condiciones de Optimalidad
85
B Simulación
B.1 Método Monte Carlo . . . . . . . . . . . . . . . . . . . . . . . . .
B.2 Simulación de Distribuciones Híbridas . . . . . . . . . . . . . .
87
87
89
C El caso del sesgo en la estimación de β∗
90
Bibliografía
93
ii
Introducción General
En las últimas tres décadas la mayor parte de las instituciones financieras han
invertido mucho tiempo y recursos en la evaluación y medición de los riesgos a los que están expuestos sus activos. De igual manera, los reguladores
de los sistemas financieros mundiales y locales han puesto un gran empeño
en la medición de los riesgos sistémicos a los que están expuestos los participantes de los distintos mercados financieros, así como en la determinación de
lineamientos generales que estos participantes deben seguir a fin de mitigar
dichos riesgos. De esta manera, se han desarrollado clasificaciones muy precisas de estos riesgos y metodologías especiales para determinar y monitorear
cada uno de éstos.
No obstante dicho esfuerzo, la crisis financiera actual ha demostrado, entre otras cosas, que este esfuerzo debe redoblarse, poniendo especial énfasis
en el seguimiento y la evolución de los riesgos, así como en una constante
revisión de la adecuación de las metodologías utilizadas para tal efecto. En
particular, respecto a esto último, deben revisarse o evaluarse los supuestos
que los correspondientes modelos hacen ya que, como cualquier otro modelo,
estos supuestos buscan, por un lado, que el modelo capture de manera aproximada la realidad del contexto de aplicación y, por el otro, que se simplifique
lo suficiente la complejidad de dicha realidad a fin de que la instrumentación
del modelo sea factible.
Este trabajo de tesis se avoca en la adecuación de las metodologías estándar de medición de riesgos. En particular, se enfoca en las adecuaciones en
los casos en que no se cumplan supuestos menos evidentes que aquellos relacionados, por ejemplo, con las medidas de riesgo usadas o las distribuciones
de pérdidas utilizadas. A saber, se considera el supuesto de que los precios de
los activos considerados reflejen toda la información disponible hasta el momento. Es decir, el presente trabajo considera la medición de riesgos cuando
este supuesto no se cumple. Esto es, cuando los precios de los activos considerados se encuentran "distorsionados". Por ejemplo, cuando la variabilidad
de los precios no refleja la verdadera incertidumbre del valor del activo. En
específico, se estudia el caso en que esta distorsión ha sido propiciada por una
alta concentración de dichos activos en el mercado financiero en que éstos se
operan.
1
Desde el punto de vista de la medición de riesgos, la distorsión de los
precios de los activos puede conllevar varios problemas. Entre otros, se tiene
los siguientes:
• Desde el punto de vista de una institución reguladora, se puede subestimar el riesgo sistémico del mercado correspondiente.
• Desde la perspectiva de un participante, puede significar una pérdida
inesperada, por ejemplo, en el caso de que dicho participante haya aceptado dichos activos como colateral de una operación crediticia.
• Desde la óptica del mismo tenedor del activo concentrado, éste esta sujeto al riesgo de que el precio de dicho activo sea impugnado por una
institución reguladora.
Para tal efecto, se considera el riesgo de mercado, dado que es el tipo de
riesgo más sencillo de distinguir y para el cual existe un consenso universal
respecto a su definición; y se toma en cuenta como motivación, una situación
específica observada recientemente en el mercado nacional de instrumentos
de renta fija. A saber, el comportamiento, un tanto peculiar, del Bono M Diciembre 2007, el cual cerca de su fecha de vencimiento mostró una distorsión
notable de su precio debido a la alta concentración de la tenencia del mismo
por un solo participante del mercado. En particular, como se puede apreciar
en la Figura 1, la variación diaria porcentual de los precios de dicho bono,
medida en términos de la desviación estándar, experimentó una reducción
drástica una vez que la tenencia de toda la emisión del título estuvo en manos
de un solo participante1 . Dicha reducción de la variabilidad conlleva, como
se demuestra más adelante en este trabajo de tesis, una subestimación importante del riesgo de mercado.
En este trabajo de tesis se desarrollan dos metodologías para medir el
riesgo de mercado, las cuales tienen dos características comunes:
• Parten del supuesto estándar de una distribución de pérdidas Gaussiana.
• Utilizan el Valor en Riesgo (VaR) y el Valor en Riesgo Condicional (CVaR)
como medidas de riesgo.
La primera de estas características busca que la metodología estándar se
adecúe solo si es necesario, en cuyo caso se desviará de ésta, dependiendo de
cada metodología, lo suficiente para medir el riesgo de mercado de manera
adecuada. Por su parte, la segunda característica garantiza que ambas metodologías no solamente utilicen la misma forma de medir de riesgo, sino que
además usen dos medidas de riesgo relevantes en el ámbito financiero. El
1 La
concentración de un instrumento de deuda puede llegar a ser superior al 100% debido a
que algunos participantes del mercado pueden vender en corto dicho instrumento.
2
Fig. 1: Bono M Diciembre 2007.
VaR, que es la medida de riesgo más ampliamente utilizada, y el CVaR, el
cual está íntimamente relacionado con el VaR, que es una medida más conservadora con propiedades deseables de una medida de riesgo que el VaR
no posee en general. La primera metodología determina el "ajuste adecuado"
que debe aplicarse a la desviación estándar para estimar el riesgo de mercado utilizando la metodología estándar bajo el supuesto de una distribución
Gaussiana. Para tal efecto, se adopta un criterio para definir lo que se entiende por "ajuste adecuado". A saber, en términos de la determinación de un
Factor de Ajuste que al multiplicarse por la desviación estándar observada,
dé como resultado una desviación estándar ajustada con base en la cual se
estiman simultáneamente el VaR y CVaR de la manera "más precisa posible".
Es decir, de manera tal que el VaR y CVaR estimados, utilizando la desviación
estándar ajustada, se parezcan lo "más posible" al VaR y CVaR observados, en
términos de la desviación cuadrática de los valores observados y estimados
correspondientes.
La segunda metodología, en lugar de ajustar el parámetro de desviación
estándar, incorpora la posibilidad de realización de un evento de estrés en el
cual la distribución de pérdidas es distinta a la distribución Gaussiana que
es considerada bajo condiciones normales. De esta manera, lo que se busca
es determinar la probabilidad de dicho evento de estrés la cual, junto con la
distribución de pérdidas considerada en este evento, permite construir una
Distribución Híbrida a partir de la cual se mide el riesgo de la manera "más
precisa posible" en el mismo sentido que se considera en la primer metodología.
Ambas metodologías se pueden aplicar a cualquier distribución de pérdidas observada o considerada y presentan varias propiedades teóricas atracti-
3
vas. Entre otras, se encuentran las siguientes:
• Bajo ciertos supuestos, los cuales se cumplen típicamente en la práctica,
los modelos matemáticos asociados con cada metodología tienen solución.
• La formulación de ambos modelos permite asignar el peso relativo que
se le da al CVaR con respecto al VaR. Por lo tanto, el valor de dicha
ponderación, la cual denominamos δ , se puede asociar, al menos intuitivamente, con un cierto nivel de aversión al riesgo.
• Tanto los Factores de Ajuste como las Distribuciones Híbridas se pueden
caracterizar en términos de una variable de referencia que determine la
forma de la distribución de pérdidas (e. g. el nivel de concentración de
ciertos activos).
• La adición o inclusión de otras medidas de riesgo distintas al VaR y
CVaR es relativamente fácil.
• La incorporación de restricciones adicionales sobre los Factores de Ajuste
o las Distribuciones Híbridas es relativamente sencilla.
Es importante mencionar que aunque el objetivo primario de las metodologías aquí desarrolladas fue la medición del riesgo de mercado en condiciones
propicias para la distorsión de los precios, dichas metodologías se pueden
aplicar para adecuar la metodología estándar por cualquier característica de
la distribución de pérdidas que se aleje de los supuestos de dicha metodología.
Las metodologías desarrolladas se aplicaron al caso del Bono M Diciembre 2007, suponiendo que se desea medir el riesgo de la posición en dicho
bono. Para el caso de la metodología de Factores de Ajuste, se obtuvieron, en
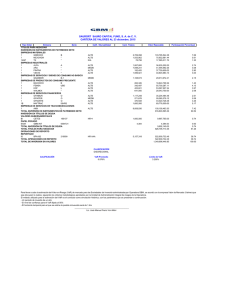
entre otros resultados, que los Factores de Ajuste, para un nivel de confianza
del 99%, varían en un rango de [1.38, 1.67], lo que significa incrementar el
parámetro de desviación estándar entre un 38% y un 67%. Por su parte, para
el caso de las Distribuciones Híbridas se obtuvieron, entre otras cosas, que las
probabilidades de estrés se encuentren en un rango de [0.00344%, 3.81709%]
considerando un nivel de confianza en el cálculo del VaR y CVaR de 95%.
En los resultados obtenidos para ambas metodologías, se observó que tanto
los Factores de Ajuste como las probabilidades de estrés de las Distribuciones
Híbridas se incrementan conforme el parámetro de aversión al riesgo así lo
hace.
4
Capítulo 1
Preliminares
En este capítulo se presentan los conceptos y resultados teóricos necesarios
para los temas que son abordados en los capítulos posteriores y se encuentra
organizado de la siguiente manera: en la Sección 1.1 se presentan conceptos
básicos de probabilidad; en la Sección 1.2 se introduce el concepto de medidas
de riesgo; en la Sección 1.3 se definen los conceptos de VaR y CVaR; en la Sección 1.4 se dan fórmulas explícitas, bajo ciertas condiciones, de las derivadas
del VaR y CVaR con respecto al nivel de confianza; en las Secciones 1.5 y 1.6
se estudian el VaR y el CVaR de las distribuciones normal y t no central, respectivamente; finalmente, en la Sección 1.7 se exponen algunos resultados de
la Teoría de Valores Extremos.
1.1
Conceptos Básicos de Probabilidad
En esta sección se establecen algunos resultados y definiciones que serán utilizadas en secciones posteriores del presente trabajo.
Definición 1.1 (σ-álgebra). Una colección de subconjuntos de Ω es una σ-álgebra,
denotada S , si satisface las siguientes tres propiedades:
1. ∅ ∈ S .
2. Si A ∈ S entonces Ac ∈ S .
3. Si A1 , A2 , . . . ∈ S entonces ∪i∞=1 Ai ∈ S .
Definición 1.2 (Medida de Probabilidad). Dado un conjunto Ω y una σ-álgebra
S de subconjuntos de Ω, una medida de probabilidad P es una función con
dominio S que satisface:
1. P[ A] ≥ 0 para toda A ∈ S .
5
2. P[Ω] = 1.
3. Si A1 , A2 , . . . ∈ S son conjuntos disjuntos, entonces P[∪i∞=1 Ai ] = ∑i∞=1 P[ Ai ].
Definición 1.3 (Espacio de Probabilidad). Un espacio de probabilidad es una
tríada (Ω, S , P) donde Ω es un conjunto cualquiera, S es la σ-álgebra de
subconjuntos de Ω, y P es una medida de probabilidad definida sobre S .
Definición 1.4 (Variable Aleatoria). Sea (Ω, S , P) un espacio de probabilidad.
Una variable aleatoria es una función X : Ω → R tal que para toda a ∈ R
{ω ∈ Ω| X (ω ) ≥ a} ∈ S .
(1.1)
Un caso particular de una variable aleatoria, es la función indicadora de
un conjunto A ∈ S definida por:
1 si x ∈ A
(1.2)
1 A (x) =
0 si x ∈
/A
Definición 1.5 (Función de Distribución Acumulada). Sea (Ω, S , P) un espacio de probabilidad y X : Ω → R una variable aleatoria, entonces
FX (y) = P[{ω ∈ Ω| X (ω ) ≤ y}] = PX [(−∞, y)]
(1.3)
es la función de distribución acumulada (FDA) correspondiente a la variable
aleatoria X.
Definición 1.6. Sea X una variable aleatoria con función de distribución acumulada dada por F, si existe una función integrable f tal que
FX ( x ) =
Z x
−∞
f (z)dz
(1.4)
se dirá entonces que X es una variable aleatoria continua. La función f será
llamada la función de densidad correspondiente a X.
Definición 1.7. Sea (Ω, S , P) un espacio de probabilidad. Las variables aleatorias X y Y se distribuyen de manera idéntica si para todo conjunto A ∈ S se
tiene que
P [ X ∈ A ] = P [Y ∈ A ]
(1.5)
La distribución de una variable aleatoria queda totalmente caracterizada
por su FDA como se establece en la siguiente proposición.
Proposición 1.1. Dos variables aleatorias X y Y se distribuyen de forma idéntica si
y sólo si tienen la misma FDA.
Demostración. Ver demostración del Teorema 1.5.2 de Casella & Berger (1990).
6
Definición 1.8 (Valor Esperado). Sea X una variable aleatoria con FDA dada
por F. El valor esperado de X, denotado E[ X ], se define como
E[ X ] =
siempre que
Z ∞
−∞
Z ∞
−∞
xdF ( x )
(1.6)
| x |dF ( x )
exista.
Definición 1.9 (Varianza). Sea X una variable aleatoria, la varianza de X se
define como
V [ X ] = E[( X − E[ X ])2 ]
(1.7)
siempre que el valor esperado exista.
1.2
Medidas de Riesgo
En esta sección se definen las medidas de riesgo y se describen algunas de sus
propiedades generales. En particular, se establece la propiedad de coherencia
de una medida de riesgo, en el sentido de Artzner et al. (1999).
Para introducir el concepto de medidas de riesgo, se representará el valor
de una posición financiera como una variable aleatoria definida dentro de un
espacio de probabilidad (Ω, S , P).
Definición 1.10 (Medida de Riesgo). Sea D un conjunto de posiciones financieras. Se dirá que la función M : D → R es una medida de riesgo si
y sólo si satisface las siguientes propiedades:
• Monotonía: Para toda X ∈ D y Y ∈ D con X ≤ Y c.s. (casi seguramente1 ) se tiene que
M ( X ) ≥ M (Y ) .
• Invariante bajo Traslaciones: Para toda m ∈ R se cumple
M ( X + m) = M ( X ) − m.
La propiedad de monotonía significa que si una posición tiene un valor
mayor o igual al valor de otra posición finaciera, bajo cualquier escenario,
entonces está última posición se considera más riesgosa que la primera. Por
su parte, la propiedad de invarianza bajo traslaciones indica que si se agrega
1 Una propiedad se satisface casi seguramente para una variable aleatoria X si se cumple para
todos puntos de su dominio, excepto posiblemente para algún subconjunto con probabilidad
cero.
7
un monto m de efectivo, o de activo libre de riesgo, a una posición financiera,
entonces el riesgo de está disminuye por el mismo monto m.
Es importante notar que la propiedad de invarianza implica en particular
que si el monto de efectivo que se agrega a la posición es precisamente el
riesgo de la posición, entonces el riesgo se neutraliza. Esta observación se
formaliza en el siguiente resultado.
Lema 1.1. Sea X una posición financiera y M una medida de riesgo, de acuerdo a la
Definición 1.10. Entonces, si se agrega una cantidad de efectivo igual al riesgo de la
posición M( X ), el riesgo de la nueva posición, X + M( X ), se neutraliza.
Demostración. Por la propiedad de invarianza bajo traslaciones, se cumple que
M( X + m) = M( X + M ( X )) = M ( X ) − M( X ) = 0.
Por lo tanto, el riesgo de la nueva posición es de cero.
Definición 1.11 (Medida de Riesgo Coherente). Sea M : D → R una medida
de riesgo. Se dirá que M es coherente si satisface las siguientes propiedades:
• Homogeneidad Positiva: Para toda X ∈ D y λ ≥ 0 se cumple que
M (λX ) = λM( X ).
• Subaditividad: Para toda X, Y ∈ D se satisface
M ( X + Y ) ≤ M ( X ) + M (Y ) .
La homogeneidad positiva indica que si la posición se incrementa por un
factor positivo entonces el riesgo se incrementa por el mismo factor2 . La
subaditividad indica que si dos posiciones se combinan en una sola posición,
entonces el riesgo de combinar las posiciones es menor o igual a la suma de
sus riesgos considerados por separado. Resulta ser que la subaditividad está
intimamente relacionada con la propiedad de convexidad como se establece
en la siguiente proposición:
Proposición 1.2. Sea M una medida de riesgo que satisface la propiedad de homegeneidad positiva, entonces M es una función convexa si y sólo si es subaditiva.
Demostración. Sean X y Y dos posiciones financieras y M una medida de
riesgo homogenea positiva. Supóngase que M es subaditiva y sea 0 ≤ λ ≤ 1.
Entonces, se cumple que
M (λX + (1 − λ)Y ) ≤ M (λX ) + M((1 − λ)Y )
= λM( X ) + (1 − λ) M(Y ).
2 Este
axioma no se cumple si existe un riesgo de liquidez, ya que en ese caso el riesgo de la
posición aumentará más rápido que el tamaño de la misma.
8
Por lo tanto, M es una función convexa. Para demostrar el recíproco supóngase que M es una medida de riesgo convexa. Entonces se sigue que
1
1
1
M(X + Y ) = M
X+ Y
2
2
2
1
1
≤ M ( X ) + M (Y ) ,
2
2
de donde,
M ( X + Y ) ≤ M ( X ) + M (Y ) .
Luego entonces, M es una medida de riesgo subaditiva.
1.3
Los Conceptos de VaR y CVaR
En esta sección se definen los conceptos de Valor en Riesgo (VaR) y Valor en
Riesgo Condicional (CVaR) y se demuestra que son medidas de riesgo en el
sentido de la Definición 1.10. Asimismo, se exponen algunas de sus ventajas
y desventajas más importantes.
Definición 1.12 (VaR). El Valor en Riesgo o VaR de una posición financiera X
a un nivel de confianza α se define como:
VaRα ( X ) = inf{ x ∈ R | P[− X ≤ x ] ≥ α}
(1.8)
Es decir el VaR no es más que el percentil más pequeño de orden α de la
distribución de pérdidas asociadas a la posición financiera X. En ocasiones se
asociará directamente una función de distribución acumulada FX a las pérdidas de la posición financiera X y estará dada por:
FX ( x ) = P[− X ≤ x ].
(1.9)
El subíndice X se omitirá para simplificar la notación en caso de que se sobreentienda por el contexto que se hace referencia a la variable aleatoria X.
Dada una variable aleatoria X, El VaR para un nivel de confianza α estará
dado por VaRα = F ← (α) = inf{ x ∈ R | F ( x ) ≥ α}. Para ilustrar lo anterior se
presenta una posible función de distribución acumulada F en la Figura 1.1 y
el correspondiente valor de VaRα = F ← (α) en la Figura 1.2. Obsérvese que el
VaR esta definido para toda α ∈ (0, 1), inclusive para el valor x = 3 donde F
presenta una discontinuidad. Asimismo el VaR presenta una discontinuidad
en α = 1/3 debido a que F ( x ) = 1/3 para toda x ∈ [1, 2].
Proposición 1.3. El VaR es una medida de riesgo.
9
1
0.8
0.6
0.4
0.2
0
−3
−2
−1
0
1
2
3
4
5
Fig. 1.1: Gráfica de la FDA
3
2.5
2
1.5
1
0.5
0
−0.5
−1
0
0.2
0.4
0.6
Fig. 1.2: Gráfica del VaRα
10
0.8
1
Demostración. Sean X y Y dos posiciones financieras, entonces si X ≤ Y se
tiene que − X ≥ −Y, por lo que
{ ω ∈ Ω | − X ( ω ) ≤ x } ⊂ { ω ∈ Ω | − Y ( ω ) ≤ x },
de donde
P[− X ≤ x ] ≤ P[−Y ≤ x ]
para toda
x ∈ R.
Entonces para toda x ∈ R y para toda α ∈ [0, 1], tal que P[−Y ≤ x ] ≥ α, se
tendrá que P[− X ≤ x ] ≥ α. Por lo tanto dado un nivel de confianza α se tiene
que
inf{ x ∈ R | P[− X ≤ x ] ≥ α} ≥ inf{ x ∈ R | P[−Y ≤ x ] ≥ α}
o equivalentemente, que VaRα ( X ) ≥ VaRα (Y ).
La propiedad de Invarianza bajo Traslaciones se sigue de
VaRα ( X + m) = inf{ x ∈ R | P[−( X + m) ≤ x ] ≥ α}
= inf{ x ∈ R | P[− X ≤ x + m] ≥ α}
= inf{y − m, y ∈ R | P[− X ≤ y] ≥ α}
= inf{y ∈ R | P[− X ≤ y] ≥ α} − m
= VaRα ( X ) − m.
Una de las desventajas del VaR es que en general no es una medida subaditiva, como se ilustra en el siguiente ejemplo:3
Ejemplo 1.1. Considérense dos bonos distintos A y B de forma tal que sus
probabilidades de incumplimiento sean mutuamente excluyentes (es decir si
el bono A incumple en su pago entonces el bono B no incumple y viceversa).
Un portafolio compuesto de ambos bonos puede tener un VaR global mayor
a la suma de los VaR individuales. Por ejemplo, supóngase que ambos bonos
tienen como valores de recuperación 70 y 90 con probabilidades de 3% y 2%
respectivamente, y que en el resto de los casos se pueden redimir por un valor
de 100. Las distribuciones de probabilidad de los bonos A, B y del portafolio
compuesto por ambos bonos se resumen en la Tabla 1.1.
Asumiendo que el valor inicial de cada bono es simplemente el valor esperado del payoff como se describe en la Tabla 1.1, este puede ser fácilmente
calculado mediante dicha tabla. Por ejemplo, para el bono A se tiene un valor
inicial de
70 · 3% + 90 · 2% + 100 · 95% = 98.9
y para el portafolio A+B se tiene un valor inicial de
170 · 6% + 190 · 4% + 200 · 90% = 197.8
Notando que la pérdida potencial en cada escenario esta dada por el valor
incial menos el valor del rescate de cada bono, se obtiene la Tabla 1.2.
3 El
Ejemplo 1.1 fue tomado de Acerbi et al. (2001).
11
Tab. 1.1
Evento
A
B
A+B
Prob
E1
E2
E3
E4
E5
70
90
100
100
100
100
100
70
90
100
170
190
170
190
200
3%
2%
3%
2%
90%
A
B
A+B
98.9
8.9
98.9
8.9
197.8
27.8
Tab. 1.2
Valor inicial
VaR 95%
A partir de dicha tabla se puede observar que VaR95% ( A + B) > VaR95% ( A) +
VaR95% ( B). Por ende el VaR no es una medida de riesgo subaditiva en este
caso.
Para remediar algunas de las desventajas del VaR, incluyendo la falta de
subaditividad, se introduce el concepto de CVaR, definido a continuación.
Definición 1.13 (CVaR). El Valor en Riesgo Condicional o CVaR de una posición financiera X para un nivel de confianza α se define como:
CVaRα ( X ) = El valor esperado de la α-cola de la distribución de pérdidas FX
donde la distribución en cuestión esta dada por
(
FX (z)−α
para z ≥ VaRα ( X )
α
1− α
FX (z) =
0
para z < VaRα ( X )
(1.10)
A continuación se demuestra que el CVaR es una medida de riesgo.
Proposición 1.4. El CVaR es una medida de riesgo.
Demostración. Sean X y Y dos posiciones financieras. Si X ≤ Y entonces se
sigue que P[− X ≤ x ] ≤ P[−Y ≤Rx ], por lo que FXR( x ) ≤ FY ( x ), lo cual implica
∞
∞
que FXα ( x ) ≤ FYα ( x ), de donde −∞ zdFXα ( x ) ≥ −∞ zdFYα ( x ), o equivalentemente, CVaRα ( X ) ≥ CVaRα (Y ).
12
Para demostrar que el CVaR es invariante bajo traslaciones, considérese el
caso en que Y = X + m, para ese caso se tiene que
FY ( x ) = P[−Y ≤ x ] = P[−( X + m) ≤ x ] = P[− X ≤ x + m] = FX ( x + m)
por definición
(
FYα (z)
=
FY (z)−α
1− α
0
para
para
z ≥ VaRα (Y )
z < VaRα (Y )
(1.11)
por ende
(
FYα (z)
=
FX (z+m)−α
1− α
0
para
para
z + m ≥ VaRα ( X )
z + m < VaRα ( X )
por lo que FYα (z) = FXα (z + m), luego entonces
Z ∞
−∞
zdFYα (z) =
=
=
Z ∞
−∞
Z ∞
−∞
Z ∞
−∞
zdFXα (z + m)
(y − m)dFXα (y)
ydFXα (y) − m
Z ∞
−∞
dFXα (y)
= CVaRα ( X ) − m.
Proposición 1.5. El CVaR es una medida de riesgo coherente.
Demostración. Por la proposición anterior se tiene que el CVaR es una medida
de riesgo. Para demostrar que es coherente considerénse dos posiciones financieas X y Y cualesquiera. Para demostrar la homgeneidad positiva del CVaR
considérese el caso en que Y = λX con λ > 0, entonces:
FY ( x ) = P[−λX ≤ x ] = P[− X ≤ x/λ] = FX ( x/λ)
por definición se tiene que
(
FαY (z) =
FY (z)−α
1− α
0
para
para
sustituyendo (1.12) en (1.13) se tiene que
(
FX ( λz )−α
α
para
1− α
FY (z) =
0
para
13
(1.12)
z ≥ VaRα (Y )
z < VaRα (Y )
(1.13)
z/λ ≥ VaRα ( X )
z/λ < VaRα ( X )
(1.14)
por lo que FYα (z) = FXα (z/λ) para toda z ∈ R, de donde se sigue que
CVaRα (Y ) =
=
=
Z ∞
−∞
Z ∞
−∞
Z ∞
zdFYα (z)
zdFXα (z/λ)
λydFXα (y)
−∞
Z ∞
=λ
−∞
ydFXα (y)
= λ CVaRα ( X ).
Rockafellar & Uryasev (2002) demuestran la convexidad de CVaRα , esto aunado a la Proposición 1.2 demuestra que el CVaR es una medida de riesgo
coherente.
En el caso de que la distribución de la variable aleatoria correspondiente
a la distribución de pérdidas F sea continua, el CVaR no es más que el valor
esperado de las pérdidas que exceden al VaR, como se detalla y demuestra
continuación.
Proposición 1.6. Sea X una posición financiera continua con función de distribución
de pérdidas FX , entonces
CVaRα ( X ) = E[− X | − X > VaRα ]
(1.15)
Demostración. Sea f la función de densidad correspondiente a la distribución
FX , se sigue que
CVaRα ( X ) =
=
=
=
Z ∞
−∞
zdFXα (z)
1
1−α
R∞
VaRα
Z ∞
VaRα
z f (z)dz
z f (z)dz
1 − F (VaRα )
E[− X 1{− X >VaRα } ]
P(− X > VaRα )
= E[− X | − X > VaRα ]
1.4
Derivada del VaR y CVaR
En esta sección se obtienen fórmulas generales de las derivadas del VaR y
CVaR con respecto al nivel de confianza α, para el caso en que la función
14
de distribución acumulada es estrictamente creciente y diferenciable. Estas
fórmulas serán de utilidad cuando se analice el comportamiento del factor de
ajuste con respecto al nivel de confianza en el Capítulo 2.
Lema 1.2. Sea F una función de distribución acumulada asociada a una variable
aleatoria X. Supóngase que F es una función estrictamente creciente y diferenciable
entonces
∂ CVaR( X )
∂ VaR( X )
y
∂α
∂α
existen y sus derivadas estan dadas por:
∂ VaR( X )
1
=
−
∂α
f ( F 1 (α))
∂ CVaR( X )
1
E([ X − VaRα ( X )]+ )
=
∂α
(1 − α )2
(1.16a)
(1.16b)
Demostración. Por definición se tiene que:
VaRα ( X ) = F ← (α) = inf{t ∈ R | F (t) ≥ α}
(1.17)
Cómo F es estrictamente creciente, F es una función inyectiva. Además si F es
diferenciable en α, será continua, por lo que para cada α ∈ (0, 1) existirá t ∈ R
tal que F (t) = α y por ende la función F será suprayectiva también4 . Luego
entonces F −1 existe y F ← (α) = F −1 (α) para toda α ∈ (0, 1). Así se tendrá que:
∂ VaR
=
∂α
1
dF dα F −1 (α)
=
1
f ( F −1 (α))
(1.18)
El segundo resultado es consecuencia directa de la existencia de F −1 y de la
proposición 13 en Rockafellar & Uryasev (2002).
1.5
El VaR y CVaR de una distribución normal
La distribución normal es una de las distribuciones de probabilidad más útiles
en el estudio del comportamiento de los activos financieros. En el presente trabajo se recurrirá con frecuencia a la distribución normal para estudiar el riesgo
de los bonos gubernamentales y como punto de referencia para estudiar otras
distribuciones de riesgo. En particular, en esta sección se deducirán fórmulas
explícitas para el cálculo del VaR y CVaR de una distribución normal.
La función de densidad de una distribución normal5 con media µ y desviación estándar σ está dada por
4 Este
último punto es un tanto sutil y posiblemente valga la pena detallarlo más. Si α ∈ (0, 1)
como F es una función de distribución acumulada existirán t∗ y t∗ tales que F (t∗ ) ≥ α y F (t∗ ) < α,
aplicando el teorema del valor intermedio sabemos que existe t ∈ [t∗ , t∗ ] tal que F (t) = α.
5 En ocasiones se hará referencia a la distribución normal como distribución Gaussiana.
15
1
( x − µ )2
f (x) = √
exp −
2σ2
2π
y tiene como función de distribución acumulada N( x ) =
(1.19)
Rx
−∞
f (z)dz.
Proposición 1.7. Dado un nivel de confianza α ∈ (0, 1), para una variable aleatoria
que se distribuye según una normal con media µ y desviación estándar σ se tiene que:
VaRα = σN−1 (α) + µ
CVaRα =
√
(1.20a)
!
σ
2π (1 − α)
exp
2
− N −1 ( α )
2
!
+µ
(1.20b)
Demostración. Sea m(z) = (z − µ)/σ entonces por definición
Z VaRα
z−µ 2
1
√ exp −
dz
α=
2σ
−∞
2π
Z m(VaRα )
1
− m2
√ exp
=
dm
2
−∞
2π
= N(m(VaRα ))
por ende m−1 (N−1 (α)) = VaRα y como m−1 (z) = σz + µ se obtiene la fórmula
del VaR descrita.
Para demostrar la fórmula del CVaR nótese que la función de densidad de
la cola de la distribución para valores de z mayores a VaRα es
(
−(z−µ)2
1
√
exp
para z ≥ VaRα
2
2σ
2πσ(1−α)
f α (z) =
0
para z < VaRα
Por lo que:
CVaRα =
=
Z ∞
VaRα
Z ∞
z f α (z)dz
√
VaRα
= √
= √
=
=
1
2πσ(1 − α)
1
2πσ (1 − α)
σ2
z exp
Z ∞
m(VaRα )
Z ∞
( z − µ )2
dz
2σ2
(σm + µ)e−m
me−m
2 /2
2 /2
σdm
dm + √
σµ
Z ∞
e−m
2 /2
dm
2πσ(1 − α) m(VaRα )
!
! σ
m(VaRα )2
µ
√
exp −
+
1 − N(m(VaRα ))
2
1−α
2π (1 − α)
!
!
2
σ
N −1 ( α )
√
exp −
+µ
2
2π (1 − α)
2πσ (1 − α)
m(VaRα )
16
donde la última igualdad se sigue del hecho de que m(VaRα ) = N−1 (α) y
N(m(VaRα )) = α.
Los siguientes corolarios caracterizan el VaR y CVaR de cualquier distribución normal en términos del VaR y CVaR de una distribucíón normal estándar,
así como su comportamiento respecto a cambios en el nivel de confianza. Estos resultados serán aplicados en el Capítulo 2.
Corolario 1.1. Sean χα y ηα el VaRα y CVaRα de una normal estándar respectivamente, entonces el VaRα y CVaRα de una normal con media µ y desviación estándar
σ están dados por:
VaRα = σχα + µ
(1.21a)
CVaRα = σηα + µ
(1.21b)
Demostración. Se sigue inmediatamente de la Proposición 1.7.
Corolario 1.2. El VaR y CVaR de una distribución normal estándar son funciones
infinitamente diferenciables en α ∈ (0, 1) y sus primeras dos derivadas están dadas
por:
1
dχ
=
dα
(1 − α ) ηα
ηα − χ α
dη
=
dα
1−α
2
d χ
χα
=
dα2
(1 − α)2 ηα2
(1.22b)
2(ηα − χα ) − 1/ηα
d2 η
=
dα2
(1 − α )2
(1.22d)
(1.22a)
(1.22c)
Demostración. De la Proposición 1.7 se puede ver que tanto el VaRα como
el CVaRα son composiciones de funciones infinitamente diferenciables en el
intervalo (0, 1). Asimismo sus derivadas de cualquier orden pueden ser obtenidas mediante un cálculo directo como se detalla a continuación para las
derivadas de primer y segundo orden:
dχ
=
dα
1
dN dα N −1 ( α )
=
1
2
exp(−N−1 (α) /2)
√
=
1
2
(1−α) exp(−N−1 (α) /2)
√
2π
17
2π (1−α)
=
1
(1 − α ) ηα
dη
d
=
dα
dα
√
−1
!
1
e
2π (1 − α)
2
−N−1 (α) /2
2
−1
2
e−N (α) /2
e−N (α) /2
− √
= √
2
2π (1 − α)
2π (1 − α)
ηα
ηα χ α
=
−
1 − α (1 − α ) ηα
ηα − χ α
=
1−α
d2 χ
d
=
2
dα
dα
!
√
2π (1 − α)
dχ
χα
dα
!
d
dα
e−N
−1 (α )2 /2
1
1
d
1
+
ηα
1 − α dα ηα
ηα − χ α
=
−
(1 − α)2 ηα (1 − α)2 ηα2
χα
=
(1 − α)2 ηα2
d2 η
=
dα2
=
1
1−α
1
d ( ηα − χ α )
(1 − α ) − ( ηα
dα
2
=
+
1
−α)
− χα ) d(1dα
(1 − α )
ηα − χ α −
+ ( ηα − χ α )
1
ηα
(1 − α )2
2(ηα − χα ) − 1/ηα
(1 − α )2
A partir de (1.22a)-(1.22d) se puede deducir el comportamiento global de
χα y ηα . A saber, de (1.22a) y (1.22b) se sigue inmediatamente que tanto χα
como ηα son funciones estrictamente crecientes en α. Además, de (1.22c) se
deduce que χα tiene un punto de inflexión en α = 0.5 y de (1.22d) que ηα tiene
un punto de inflexión en α ≈ 0.291. Por último, de (1.22c) se sigue que χα es
una función cóncava para α < 0.5 y convexa para α > 0.5 y de (1.22d) que ηα
es una función cóncava para α < 0.291 y convexa para α > 0.291.
Las observaciones anteriores se ilustran en la Figura 1.3 donde se grafican
χ α y ηα .
18
VaRα y CVaRα de una distribución normal estándar
3
2
1
0
−1
−2
χα
ηα
−3
0
0.1
0.2
0.3
0.4
0.5
α
0.6
0.7
0.8
0.9
1
Fig. 1.3: Gráfica del VaRα y CVaRα para una distribución normal estándar.
1.6
El VaR y CVaR de una distribución t no central
La distribución t no central, al igual que la distribución normal, es ampliamente utilizada en la modelación de riesgos financieros. Esto debido principalmente a que puede modelar los fenómenos de alta curtosis y colas pesadas
presentadas comúnmente en las series financieras, y a su relativamente sencillo tratamiento analítico.
La función de densidad de una distribución t no central6 es de la forma
f T (x) =
Γ
Γ
ν
2
ν +1
2
√

πφν
 1 + (x
− µ )2
φν
−( 1+2 ν )

(1.23)
donde µ es un parámetro de localización, φ es un parámetro de dispersión y
ν es un parámetro de forma o de grados de libertad.
Cabe mencionar que la distribución t de Student, también llamada t estándar, asume µ = 0, φ = 1 y ν entero.
La función de distribución acumulada de la distribución t estándar con ν
grados de libertad será denotada Tν .
A continuación se enuncian y derivan fórmulas explícitas para el VaR y
CVaR de la distribución t no central.
Proposición 1.8. Dado un nivel de confianza α ∈ (0, 1) para una variable aleatoria
6 Existen parametrizaciones más generales de una distribución t no central, sin embargo, la
parametrizacion descrita por la ecuación 1.23 es lo suficientemente general para los propósitos
del presente trabajo.
19
con distribución t no central con parámetros µ, φ y ν > 1 se tiene que:
p
1
VaRα = φT−
ν (α) + µ
√ 1
2 f ( T−1 ( α )) φν
T−
t
ν (α)
ν
CVaRα =
1+
+µ
ν−1
ν
1−α
(1.24)
(1.25)
donde f t es la función de densidad de una distribución t estándar con ν grados de
libertad.
x −µ
√ ,
φ
Demostración. Sea m( x ) =
α=
=
Γ
Z VaRα
Γ
−∞
ν
2
entonces por definición
ν +1
2
√

πφν
 1 + (x
− µ )2
φν
−( 1+2 ν )
dx

−( 1+2 ν )
2
m

√ 1+
dm
ν
Γ ν2
πν
Γ
Z m(VaRα )
−∞
ν +1
2

= Tν (m(VaRα ))
1
por ende m−1 (T−
ν ( α )) = VaRα de donde se sigue que VaRα =
En el caso del CVaR se tiene que
1
CVaRα =
1−α
Z ∞
1
1−α
Z ∞
=
VaRα
√
1
φT−
ν ( α ) + µ.
−( 1+2 ν )
2
(
x
−
µ
)

1+
√
dx
φν
Γ ν2
πφν
1
T−
ν (α)
Γ
Γ
ν +1
2
x

√
ν +1
( φm + µ)
2
1+
√ √
Γ ν2
πν φ

m2
ν
−( 1+2 ν )

Z ∞
p
1
( φm + µ) f t (m)dm
1 − α T−ν 1 (α)
√ Z ∞
Z ∞
φ
1
=
m
f
(
m
)
dm
+
µ f t (m)dm
t
1 − α T−ν 1 (α)
1 − α T−ν 1 (α)
=
(1.26)
p
φdm (1.27)
(1.28)
(1.29)
donde se ha hecho uso del cambio de variable de x por m en (1.27). Haciendo
el cambio de variable y = m2 /v en la primera integral de (1.29) y tomando
20
C=
1
Γ( ν+
2 )
√
Γ( 2ν ) πν
se tiene que:
−( 1+2 v )
m2
m f t (m)dm = −1 Cm 1 +
dm
1
ν
T−
Tν (α)
ν (α)
Z ∞
v
1+ ν
= T −1 ( α )2 C
(1 + y)−( 2 ) dy
ν
2
ν
∞
1+ ν
C v2 (1 + y)−( 2 )+1 =
T −1 ( α )2
− 1+2 ν + 1
Z ∞
Z ∞
ν
ν
∞
ν
−( 1+2 ν ) =
(1 + y ) C (1 + y )
T−ν 1 (α)2
1−ν
ν
1 ( α )2 T−
ν
1
1+ ν
f t (T−
=−
ν ( α )).
1−ν
ν
Para obtener la segunda integral de (1.29) nótese que
Z ∞
1
T−
ν (α)
f t (m)dm = 1 −
Z T −1 ( α )
ν
−∞
f t (m)dm = 1 − α
por lo que
√
φ
ν
T −1 ( α )2
µ (1 − α )
1
1+ ν
f t (T−
ν ( α )) +
1−α
ν−1
ν
1−α
√ −
1
2
−
1
φν
T (α)
f t (Tν (α))
=
1+ ν
+ µ.
ν−1
ν
1−α
CVaRα =
1.7
Teoría de Valores Extremos
En esta sección se exponen brevemente algunos de los resultados claves de la
Teoría de Valores Extremos. Para una exposición más detallada, incluyendo
las demostraciones de los resultados, se puede consultar, por ejemplo, Embrechts et al. (1997).
Definición 1.14 (Dominio de Atracción de Máximos). Sea Xn una sucesión de
variables aleatorias independientes e idénticamente distribuidas con función
de distribución acumulada dada por F y Mn = max1≤i≤n ( Xi ). Si existen dos
sucesiones an : N → R+ y bn : N → R y H ( x ) una función de distribución
no degenerada, tales que
Mn − bn
lim P
≤ x = H (x)
(1.30)
n→∞
an
21
para toda x en los puntos de continuidad de H, entonces se dice que F
pertenece al dominio de atracción de máximos de H, y a esta propiedad se le
denota F ∈ DAM( H ).
Definición 1.15 (Distribución de Extremos Generalizada). La distribución de
extremos generalizada está dada por
(
exp −(1 + ξx )−1/ξ
para ξ 6= 0,
Hξ ( x ) =
(1.31)
−
x
exp (−e )
para ξ = 0,
donde x es tal que 1 + ξx > 0 y ξ es un parámetro de forma. Si ξ > 0, H es
una distribución tipo Fréchet; si ξ < 0, H es una distribución tipo Weibull; si
ξ = 0, H es una distribución de tipo Gumbel.
Teorema 1.1 (Fisher-Tippett). Sea Xn una sucesión de variables aleatorias independientes e idénticamente distribuidas con función de distribución acumulada dada por
F. Si F ∈ DAM( H ), entonces H es una distribución de extremos generalizada de
acuerdo a la definición (1.31).
Definición 1.16 (Distribución Pareto Generalizada).
(
−1
1 − (1 + ξx/β) ξ para
Gξ,β ( x ) =
1 − exp(− x/β)
para
ξ 6= 0,
ξ = 0.
(1.32)
donde β > 0 y x ≥ 0 cuando ξ ≥ 0 mientras que 0 ≤ x ≤ − β/ξ, si ξ < 0.
Definición 1.17. Dada una variable aleatoria X con función de distribución
acumulada F, se define la función de excesos sobre el umbral u como
Fu ( x ) = P[ X − u ≤ x | X > u]
(1.33)
para 0 ≤ x < x F − u, donde x F es el extremo derecho de la distribución F
definido como x F = sup { x ∈ R| F ( x ) < 1}.
Teorema 1.2 (Pickands-Balkema-de Haan). Sea F una función de distribución
acumulada con funciones de exceso Fu , para u ≥ 0. Entonces, dado ξ ∈ R, F ∈
DAM( Hξ ) si y sólo si existe una función medible positiva β(u) tal que
lim sup Fu ( x ) − Gξ,β(u) ( x ) = 0
(1.34)
x ↑ x F 0≤ x ≤ x − u
F
donde G es la función de distribución acumulada de una v.a. Pareto Generalizada con
párametros ξ y β, definida como en (1.32).
22
Capítulo 2
Factores de Ajuste de la
Volatilidad
2.1
Introducción
El objetivo principal de este capítulo es exponer una metodología para ajustar el parámetro de desviación estándar usado para determinar el VaR y el
CVaR bajo el supuesto de normalidad de la distribución de pérdidas. Para tal
efecto, este capítulo está organizado de la siguiente manera: en la Sección 2.2
se formula matemáticamente la determinación del factor de ajuste. En la Sección 2.3 se estudian algunas de las propiedades del factor de ajuste. En la
Sección 2.4 se aplican los resultados derivados en las secciones anteriores en
el contexto de los bonos que motivaron este trabajo de tesis. En la Sección 2.5
se descomponen los factores obtenidos en la sección anterior con el objeto de
aislar otros fenómenos capturados por el factor de ajuste. En la Sección 2.6 se
aplica la metodología desarrollada, en el mismo contexto considerado en la
Sección 2.4, pero usando otra variable de referencia. En la Sección 2.7 se motiva el uso de la Teoría de Valores Extremos para una estimación más precisa
del VaR y CVaR y con base en estas estimaciones se recalculan los factores de
ajuste y se comparan con los obtenidos en secciones anteriores. Finalmente,
en la Sección 2.8 se concluye.
2.2
Formulación Matemática
Como se menciona en la introducción, el objetivo de este capítulo es, determinar el "ajuste adecuado" que debe aplicarse a la desviación estándar de
las pérdidas para estimar el riesgo de mercado de manera más precisa, bajo
condiciones de distorsión de los precios.
23
Para tal efecto, se adopta como criterio de "ajuste adecuado" la determinación de un factor de ajuste que al multiplicarse por la desviación estándar
observada, dé como resultado una desviación estándar ajustada con base en la
cual se estiman simultáneamente el VaR y el CVaR, de la manera "más precisa
posible". Es decir, de manera tal que el VaR y CVaR estimados, utilizando la
desviación estándar ajustada, se parezca lo "más posible" al VaR y CVaR observados. Concretamente, que la desviación cuadrática de los valores estimados
y observados de estas medidas de riesgo sea mínima.
En términos matemáticos, el factor de ajuste F ∗ se determina al resolver
el problema de optimización
Min (1 − δ)(VaRαE −[µ̂ E + χα (F σ̂ E )])2 + δ(CVaRαE −[µ̂ E + ηα (F σ̂ E )])2
F
(2.1)
donde 0 < δ < 1 es un parámetro que indica la ponderación relativa entre
ajustar el VaR de la distribución empírica VaRαE y el CVaR de la distribución
empírica1 CVaRαE y cuyo valor se determina a priori. Los parámetros µ̂ E y
σ̂ E son, respectivamente, la media y desviación estándar de la distribución
empírica. Las funciones χα y ηα representan, respectivamente, el VaR y CVaR
de una distribución normal estándar y pueden ser calculadas mediante las
fórmulas (1.20a) y (1.20b) del Capítulo 1.
El problema de optimización (2.1) tiene una única solución explícita, la
cual se enuncia y demuestra formalmente en el Teorema 2.1.
Teorema 2.1. Sea α ∈ (0, 1), un nivel de confianza dado. Entonces, el factor de
ajuste óptimo F ∗ que resuelve (2.1) es
F∗ =
(1 − δ)χα (VaRαE −µ̂ E ) + δηα (CVaRαE −µ̂ E )
σ̂ E [(1 − δ)χ2α + δηα2 ]
(2.2)
Demostración. Dado que la función objetivo del problema (2.1) es convexa y
diferenciable en F , basta demostrar que F ∗ satisface las condiciones de optimalidad de primer orden (ver apéndice A). Dichas condiciones se reducen en
este caso a la ecuación
0 = 2(1 − δ)(VaRαE −[µ̂ E + χα (F ∗ σ̂ E )])(−χα σ̂ E )+
2δ(CVaRαE −[µ̂ E + ηα (F ∗ σ̂ E )])(−ηα σ̂ E )
o equivalentemente a la condición
0 =F ∗ [(1 − δ)χα 2 + δηα 2 ]σ̂ E
−[(1 − δ)χα (VaRαE −µ̂ E ) + δηα (CVaRαE −µ̂ E )].
(2.3)
1 El VaR y CVaR empíricos fueron calculados a partir de la Proposición 8 de Rockafellar &
Uryasev (2002).
24
Obsérvese que δ ∈ (0, 1) implica
(1 − δ)χ2α + δηα2 > 0
(2.4)
dado que χα 6= ηα para toda α ∈ (0, 1). Por lo tanto, despejando F ∗ de (2.3)
se deduce (2.2).
2.3
Propiedades
En esta sección se estudian algunas de las propiedades elementales del factor
de ajuste F ∗ , a saber las siguientes:
• El valor de F ∗ cuando las pérdidas se comportan de acuerdo a una
distribución normal.
• Condiciones bajo las cuales F ∗ es mayor o igual a cero.
• La relación entre F ∗ y el parámetro de aversión al riesgo δ.
• La relación entre F ∗ y el nivel de confianza α.
2.3.1
Caso Normal
Si las pérdidas se distribuyeran de acuerdo a una distribución normal y se
conocieran los parámetros verdaderos de ésta, se esperaría intuitivamente que
el factor de ajuste óptimo fuese igual a uno. El siguiente resultado corrobora
matemáticamente dicha intuición.
Corolario 2.1. Supóngase que la distribución empírica de las pérdidas Π es normal
con media µ̂ E y desviación estándar σ̂ E . Entonces, F ∗ = 1 para toda δ ∈ (0, 1) y
toda α ∈ (0, 1).
Demostración. Supóngase que Π ∼ N (µ̂ E , σ̂ E ). Entonces, por el Corolario 1.1,
se cumple que
VaRαE = µ̂ E + χα σ̂ E
y
CVaRαE = µ̂ E + ηα σ̂ E
Luego entonces, por el Teorema 2.1, se tiene que
F∗ =
(1 − δ)χα (VaRαE −µ̂ E ) + δηα (CVaRαE −µ̂ E )
σ̂ E [(1 − δ)χ2α + δηα2 ]
(1 − δ)χα (σ̂ E χα + µ̂ E − µ̂ E ) + δηα (σ̂ E ηα + µ̂ E − µ̂ E )
σ̂ E [(1 − δ)χ2α + δηα2 ]
(1 − δ)χ2α + δηα2
=
(1 − δ)χ2α + δηα2
=1
=
25
Error en la estimación de F*
cuando la muestra proviene de una distribución normal
Error en la estimación de F*
cuando la muestra proviene de una distribución normal
35
Error
0.1
30
0.08
Cuantil
Densidad
25
20
15
0.06
0.04
10
0.02
5
0
0
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
0.1
0.2
0.3
Magnitud del Error
0.4
0.5
0.6
0.7
0.8
0.9
Probabilidad
(a) Densidad
(b) Cuantil
Fig. 2.1: Error en la estimación de F ∗ .
Cuando la distribución empírica de pérdidas Π sigue una distribución
normal con media µ E y varianza σ E , ambas desconocidas, el factor de ajuste
está dado por la expresión:
F∗ =
σE
(1 − δ)χα (µ E − µ̂ E ) + δηα (µ E − µ̂ E )
+
E
σ̂
σ̂ E [(1 − δ)χ2α + δηα2 ]
Por lo que basta con que ambos estimadores µ̂ E y σ̂ E sean consistentes, como
lo serían los estimadores por máxima verosimilitud, para que el factor de
ajuste óptimo F ∗ converja a 1 conforme el tamaño de la muestra se incrementa.
En la Figura 2.1 se muestra la función de densidad (histograma normalizado) y la función cuantil del error2 , dado por |F ∗ − 1| en la estimación de
F ∗ , cuando se tiene una muestra de 1000 datos proveniente de una distribución normal estándar, para un nivel de confianza del α = 95% y un valor de
δ = 0.5. Ambas gráficas fueron generadas a partir de 100,000 muestras de
1000 datos cada una, provenientes de una distribución normal estándar. Se
puede observar que la mayor parte de los errores son cercanos a cero y que la
probabilidad de tener un error mayor a 6% es prácticamente cero.
2.3.2
No Negatividad
El factor de ajuste óptimo F ∗ , definido en (2.2), no siempre es positivo. Para
ilustrar esto considerése el caso en que las pérdidas se comportan de acuerdo
a una distribución Pareto con función de densidad dada por
f (x) =
3
1
( x ),
x4 (1,∞)
(2.5)
2 En este caso coinciden el error relativo y el error absoluto, por lo cual se referirá a ambos
simplemte como el "error".
26
donde 1(1,∞) es igual a 1 si x ∈ (1, ∞) y cero en otro caso. Bajo esta distribución, el factor de ajuste F ∗ es negativo, por ejemplo, para δ ∈ [0, 0.05] y
α ∈ [0.55, 0.625] como se puede apreciar en la Figura 2.2.
Valor del Factor de Ajuste Óptimo
Valor de F* Para Una Variable Aleatoria
con Distribución Pareto
2
1.5
1
0.5
0
1
−0.5
1
0.9
0.5
0.8
0.7
0.6
Valor de α
0.5
0
Valor de δ
Fig. 2.2: Gráfica de F ∗ para el caso de una distribución Pareto, con función de
densidad dada por (2.5) y distintos niveles de confianza entre 50% y 100%.
La siguiente proposición establece condiciones suficientes para garantizar
que F ∗ ≥ 0.
Proposición 2.1. Sea δ ∈ (0, 1) y α ∈ [0.5, 1). Supóngase VaRαE ≥ µ̂ E . Entonces
F ∗ ≥ 0.
Demostración. De (2.2) se deduce que F ∗ ≥ 0 si y sólo si
(1 − δ)(VaRαE −µ̂ E )χα + δ(CVaRαE −µ̂ E )ηα ≥ 0.
Nótese que la condición anterior se puede reescribir como
(VaRαE −µ̂ E )χα + δ[(CVaRαE −µ̂ E )ηα − (VaRαE −µ̂ E )χα ] ≥ 0.
(2.6)
Por definición del CVaR se cumple que CVaRαE ≥ VaRαE y ηα ≥ χα , para toda
α ∈ (0, 1). Por lo tanto,
(CVaRαE −µ̂ E )ηα − (VaRαE −µ̂ E )χα ≥ (CVaRαE −µ̂ E )χα − (VaRαE −µ̂ E )χα
= (CVaRαE − VaRαE )χα
≥ 0,
donde la última desigualdad es consecuencia del supuesto α ∈ [0.5, 1). Luego
entonces, es claro que VaRαE ≥ µ̂ E implica (2.6) y por lo tanto se satisface que
F ∗ ≥ 0.
27
Obsérvese que la condición de suficiencia de la Proposición 2.1 para la
distribución Pareto descrita en (2.5) es equivalente a la condición3 α ≥ 0.7037.
Es decir, a que el nivel de confianza sea al menos de 70.37%. Por lo tanto,
el factor de ajuste debe ser mayor o igual a cero para niveles de confianza
mayores a 70.37%, lo cual se cumple como se puede apreciar en la Figura 2.2.
Una consecuencia importante de la Proposición 2.1 es que el factor de
ajuste F ∗ es mayor o igual a cero para cualquier distribución simétrica de
pérdidas, bajo niveles de confianza mayores o iguales a 50%. En particular, la
Proposición 2.1 garantiza que tanto la distribución normal, como la distribución t de Student tienen factores de ajuste positivos para niveles de confianza
mayores a 50%.
2.3.3
F ∗ y El Nivel de Aversión al Riesgo δ
Proposición 2.2. Sea δ ∈ (0, 1) y α ∈ (0.5, 1). Supóngase que VaRαE > µ̂ E .
F ∗ ≥ 0 si y sólo si
Entonces ∂∂δ
CVaRαE −µ̂ E
ηα
≥
E
E
χα
VaRα −µ̂
(2.7)
Demostración. Del Teorema 2.1 se tiene que
F∗ =
(1 − δ)χα (VaRαE −µ̂ E ) + δηα (CVaRαE −µ̂ E )
(1 − δ)χα 2 σ̂ E + δηα 2 σ̂ E
(ηα (CVaRαE −µ̂ E ) − χα (VaRαE −µ̂ E ))δ + χα (VaRαE −µ̂ E )
(ηα 2 σ̂ E − χα 2 σ̂ E )δ + χα 2 σ̂ E
( B − A)δ + A
=
( D − C )δ + C
=
(2.8)
donde
A ≡ χα (VaRαE −µ̂ E )
(2.9a)
ηα (CVaRαE
χα 2 σ̂ E
(2.9b)
B≡
C≡
E
−µ̂ )
D ≡ ηα 2 σ̂ E
(2.9c)
(2.9d)
Derivando (2.8) con respecto a δ se obtiene
∂F ∗
( B − A)[( D − C )δ + C ] − [( B − A)δ + A]( D − C )
=
∂δ
[( D − C )δ + C ]2
C ( B − A) − A( D − C )
=
[( D − C )δ + C ]2
3 Para
(2.10)
la distribución Pareto con función de densidad dada por (2.5) se tiene que VaRα =
3
(1 − α)−1/3 y µ = 3/2. Por ende, VaRα ≥ µ si y sólo si α ≥ 1 − 23 ≈ 0.7037.
28
Claramente el denominador de (2.10) es positivo, luego entonces
sólo si
C ( B − A ) ≥ A ( D − C ).
∂F ∗
∂δ
≥ 0 si y
(2.11)
Sustituyendo (2.9) en (2.11) y cancelando el término común χα σ̂ E , el cual es
positivo por consecuencia del supuesto α ∈ (0.5, 1), se deduce que la condición (2.11) es equivalente a
χα ηα (CVaRαE −µ̂ E ) − χα 2 (VaRαE −µ̂ E ) ≥ (VaRαE −µ̂ E )[ηα 2 − χα 2 ].
Dividiendo ambos lados de la desigualdad anterior por
χα ηα (VaRαE −µ̂ E ) > 0
se obtiene
CVaRαE −µ̂ E
ηα
χα
χα
≥
−
−
E
E
η
χ
ηα
VaRα −µ̂
α
α
o, de manera equivalente, que
CVaRαE −µ̂ E
ηα
≥
χα
VaRαE −µ̂ E
de donde se concluye (2.7).
La proposición anterior indica que, dado un nivel de confianza α, el factor
de escala F ∗ crece conforme δ se incrementa si y sólo si la pérdida en exceso,
respecto a la pérdida esperada (µ̂ E ), asociada con el CVaRα es suficientemente
grande con respecto a la correspondiente pérdida en exceso relacionada con
el VaRα , donde suficientemente grande significa mayor en una proporción de
al menos (ηα /χα − 1)%. Dicho porcentaje es la proporción en que el CVaRα
es mayor que el VaRα para el caso de una normal estándar y representa la
distancia relativa entre el CVaRα y el VaRα . Si se generaliza este concepto de
distancia relativa para cualquier distribución, la Proposición 2.2 implica que
F ∗ es creciente en δ si la distancia relativa entre el CVaRα y el VaRα para la
distribución de pérdidas Π es mayor o igual que la correspondiente distancia
relativa para una distribución normal estándar.
Una vez establecidas condiciones necesarias y suficientes para la monotonicidad de F ∗ con respecto a δ es de interés analizar la manera en que F ∗
se incrementa bajo dichas condiciones. Como se demuestra en la Proposición 2.2, entre mayor sea la aversión al riesgo, menor será el incremento de
F ∗ . Para tal efecto, se usa el siguiente lema.
Lema 2.1. Sea δ ∈ (0, 1) y α ∈ (0, 1). Entonces,
∂2 F ∗
∂F ∗
=
−
K
∂δ
∂δ2
donde K =
2( D − C )
( D −C )δ+C
> 0.
29
(2.12)
Demostración. Derivando (2.10) con respecto a δ se obtiene:
2[( D − C )δ + C ][C ( B − A) − A( D − C )]
∂2 F ∗
=−
∂δ2
[( D − C )δ + C ]4
!
!
2[( D − C )δ + C ]( D − C )
C ( B − A) − A( D − C )
=−
[( D − C )δ + C ]2
[( D − C )δ + C ]2
2( D − C )
∂F ∗
=−
( D − C )δ + C
∂δ
tomando K =
2( D − C )
( D −C )δ+C
se concluye de forma inmediata (2.12).
Proposición 2.3. Sea δ ∈ (0, 1) y α ∈ (0, 1). Entonces,
∂2 F ∗
≤0
∂δ2
si y sólo si
∂F ∗
≥0
∂δ
(2.13)
Demostración. Se sigue de forma inmediata del lema anterior.
En términos geométricos, el resultado anterior indica que F ∗ , como función de δ, es cóncava si y sólo si es creciente. Por lo tanto, cualquier condición
necesaria y suficiente para la monotonicidad de F ∗ con respecto a δ lo es también para la concavidad de F ∗ . El siguiente corolario vincula las condiciones
de monotonicidad de la Proposición 2.2 con la concavidad de F ∗ .
Corolario 2.2. Sea δ ∈ (0, 1), α ∈ (0.5, 1) y VaRαE > µ̂ E . Entonces,
sólo si se satisface la condición (2.7).
∂2 F ∗
∂δ2
≤ 0 si y
Demostración. Se concluye de manera inmediata a partir de la proposición
anterior y la Proposición 2.2.
Con el objeto de ilustrar los resultados anteriores, se grafica en la Figura 2.3a
la diferencia
CVaRα
ηα
− ,
VaRα
χα
para el caso de una distribución t de Student con 10 grados de libertad4 , considerando niveles de confianza entre 50% y 100%. Como se puede observar,
la condición (2.7) se satisface. Por lo tanto, F ∗ es creciente en δ (Figura 2.3b).
Andreev & Kanto (2005) muestran que la condición (2.7) se satisface para
cualquier nivel de curtosis entre 0 y 50, y para distintos niveles de confianza,
como son α = 90%, 95%, 97.5%, 99% y 99.5%.
4 El
VaR y el CVaR de la distribución t de Student fueron calculados usando la Proposición 1.8
del Capítulo 1.
30
Valor de F* Para Una Variable Aleatoria Con Distribución
t de Student con 10 grados de libertad
Diferencia entre el cociente del CVaR al VaR de una t de Student con
10 grados de libertad y el cociente del VaR al CVaR de una normal estándar
Valor del Factor de Ajuste Óptimo
4
3.5
3
2.5
2
1.5
1
1.15
1.1
1.05
1
0.95
0.9
1
1
0.8
0.5
0.6
0.6
0
0.5
0.55
0.7
0.75
0.8
0.6
0.65
0.85
0.9
0.95
1
Valor de α
0.8
0.4
0.4
0.2
0
Valor de δ
(b) Gráfica de F ∗
(a) Verificación de la condición (2.7)
Fig. 2.3: Distribución t de Student con 10 grados de libertad.
2.3.4
F ∗ y el Nivel de Confianza α
Al igual que los resultados de monotonicidad de F ∗ con respecto a δ obtenidos
en la Proposición 2.2, se pueden derivar condiciones de monotonicidad de F ∗
respecto al nivel de confianza α. La siguiente proposición establece la suficiencia de dichas condiciones.
Proposición 2.4. Sea δ ∈ (0, 1) y α ∈ (0, 1). Si la función de distribución acumulada correspondiente a Π es una función estrictamente creciente y diferenciable en α
F ∗ existe y ∂F ∗ ≥ 0 si y sólo si
entonces ∂∂α
∂α
K1 (VaRα −µ E ) + K2 (CVaRα −µ E ) + K3 (
∂ VaR
∂ CVaR
) + K4 (
)≥0
∂α
∂α
donde K1 , K2 , K3 y K4 son funciones de δ y α dadas por:
1 − 2χα (ηα − χα )
χ2α
2
K1 (δ, α) = −(1 − δ)
+ δ (1 − δ ) ηα
(2.14a)
(1 − α ) ηα
1−α
2
η ( ηα − χ α )
χ α ( ηα − χ α ) − 2
K2 (δ, α) = −δ2 α
+ δ (1 − δ ) χ α
(2.14b)
1−α
1−α
K3 (δ, α) = (1 − δ)2 χα 3 + δ(1 − δ)χα ηα 2
2
3
K4 (δ, α) = δ ηα + δ(1 − δ)ηα χα
2
(2.14c)
(2.14d)
Demostración. Si la función de distribución acumulada correspondiente a Π es
estrictamente creciente y diferenciable en α entonces por el Lema 1.2, ∂ VaR
∂α y
∂ CVaR
existen.
Asimismo
por
el
corolario
1.2
las
derivadas
de
χ
y
η
existen
α
α
∂α
y están dadas por (1.22a) y (1.22b).
Partiendo de la ecuación (2.2) el factor de ajuste óptimo puede expresarse
como una función del nivel de confianza α de la siguiente manera:
31
F ∗ (α) =
Q(α)
R(α)
(2.15)
donde
Q(α) = (1 − δ)χα (VaRα −µ E ) + δηα (CVaRα −µ E )
2 E
E
R(α) = (1 − δ)χα σ + δσ ηα
2
(2.16a)
(2.16b)
Partiendo de (2.15) se obtiene entonces la siguiente expresión para la derivada
de F ∗
∂F ∗
=
∂α
∂Q
∂α R ( α ) −
Q(α) ∂R
∂α
R ( α )2
(2.17)
Definiendo
S(α) ≡
∂Q
∂R
R(α) − Q(α)
∂α
∂α
(2.18)
es inmediatio notar que
∂F ∗
≥0
∂α
si y sólo si
S(α) ≥ 0
Luego entonces basta probar que (2.18) es no negativo. Desarrollando (2.18) y
cancelando el término común σ E se obtiene:
S(α) = K1 (VaRα −µ E ) + K2 (CVaRα −µ E ) + K3 (
donde K1 , K2 , K3 y K4 estan dados por (2.14)
∂ VaR
∂ CVaR
) + K4 (
) (2.19)
∂α
∂α
Una vez fijados el nivel de confianza α y el parámetro δ las constantes K1 ,
K2 , K3 y K4 pueden calcularse por medio de (2.14). Sin embargo se necesita
una forma funcional o parámetrica de la función de distribución acumulada
∂ CVaR
para poder obtener ∂ VaR
por lo que la Proposición 2.4 sólo es útil
∂α y
∂α
para estudiar distribuciones "teóricas".
2.4
Aplicaciones
En esta sección se obtienen y analizan los factores de ajuste para dos casos
particulares: el caso del Bono M Diciembre 2007, el cual corresponde al fenómeno que motivó el presente trabajo, y el caso del Bono M Junio 2011, el cual
corresponde a un bono altamente concentrado, como el Bono Diciembre M
2007, pero que a diferencia de este último, no ha mostrado una distorsión tan
significativa en sus precios. La consideración del Bono M Junio 2011 se hace
con el objeto de contrastar los factores de ajuste para dicho bono, respecto a
aquellas obtenidas para el Bono M Diciembre 2007.
32
2.4.1
Bono M Diciembre 2007
Para poder aplicar el Teorema 2.1 es necesario determinar la distribución de
pérdidas a considerar. Para tal efecto, se consideraron en primera instancia
las variaciones diarias porcentuales de los precios del Bono M Diciembre 2007,
comprendidas entre el 4 de enero del 2001 y el 30 de noviembre del 2007. Dado
que es de interés asociar el comportamiento del factor de ajuste con los altos
niveles de concentración mostrados por este bono, se determinaron las distribuciones de pérdidas empíricas de las variaciones porcentuales asociadas
con distintos niveles de concentración predeterminados. A partir de cada una
de estas distribuciones se determinaron los factores de ajuste para distintos
valores de δ, dado un nivel de confianza α. Por ejemplo, en la Figura 2.4 se
grafica F ∗ para distintos valores de δ, en el caso de concentraciones mayores
o iguales a 50% y considerando un nivel de confianza del 99%.
Valor de F* para una concentración mayor o igual al 50%
Nivel de Confianza del 99%
1.48
Valor de F*
1.46
1.44
1.42
1.4
1.38
1.36
0
0.1
0.2
0.3
0.4
0.5
0.6
Valor de δ
0.7
0.8
0.9
1
Fig. 2.4: Bono Diciembre 2007. Gráfica de F ∗ con respecto a δ, para C0 ≥ 50%
y α = 99%.
Por su parte en la Figura 2.5 se grafica el factor F ∗ como función de δ,
para un nivel de confianza del 99%, pero considerando distintos niveles de
concentración C0 .
Como se puede observar en las Figuras 2.4 y 2.5, el factor F ∗ es una función creciente respecto a δ. Esto se debe a que las distribuciones consideradas
satisfacen la condición (2.7) de la Proposición 2.2. Para ilustrar esto último, se
tabularon los valores de
ηα
CVaRαE −µ
y
χα
VaRαE −µ
en el caso de una concentración mínima de 80%, considerando distintos nive33
Valor del Factor de Ajuste Óptimo F*
Valor de F* para distintos niveles de concentración
Nivel de Confianza del 99%
1.8
1.7
1.6
1.5
1.4
1.3
0.9
0.8
1
0.7
0.6
0.4
0.6
Rango de Concentración
0.8
0.5
0.2
0
Valor de δ
Fig. 2.5: Bono Diciembre 2007. Gráfica de F ∗ para distintos niveles de concentración mínima y α = 99%.
les de confianza. Esto se muestra en la Tabla 2.1.
Tab. 2.1: Verificación de la Condición 2.7
2.4.2
α
CVaRαE −µ̂ E
VaRαE −µ̂ E
ηα
χα
95%
96%
97%
98%
99%
1.8291
1.7437
1.5074
1.4116
1.3246
1.254
1.2306
1.2059
1.1788
1.1457
Bono M Junio 2011
De la misma manera en que se procedió en la sección anterior, se obtuvieron
los factores de ajuste para el caso del Bono M Junio 2011 para distintos valores
de δ y rangos de concentración mínimos, considerando un nivel de confianza
del 99%, como se muestra en la Figura 2.6.
34
Valor del Factor de Ajuste Óptimo F*
Valor de F* para distintos niveles de concentración
Nivel de Confianza del 99%
2.8
2.6
2.4
2.2
2
0.9
0.8
0.8
0.7
0.4
0.6
Rango de Concentración
1
0.6
0.5
0.2
0
Valor de δ
Fig. 2.6: Bono Junio 2011. Gráfica de F ∗ para distintos niveles de concentración mínima y α = 99%.
2.5
Descomposición del Efecto de Distorsión
Un factor de ajuste F ∗ distinto a uno no implica necesariamente una distorsión de los precios. Esto se puede deber a otras causas. Por ejemplo, las
siguientes:
• La distribución de pérdidas no es normal.
• La distribución de pérdidas es normal, pero los parámetros estimados
no son los verdaderos.
Por esta razón, en esta sección se propone una manera de extraer el efecto
de distorsión a partir del factor de ajuste. Para tal efecto, se supone que el
factor F ∗ se descompone de la siguiente forma:
F ∗ = F N∗ F D∗
(2.20)
∗ es el factor de ajuste debido a las condiciones de mercado "nordonde F N
∗ es el factor
males" en las que no se presentan distorsiones de los precios, y F D
que se aplica adicionalmente por distorsión de los precios. Para determinar
F N∗ se considera el conjunto de aquellos títulos que no presentan dicha distorsión. En el caso particular de los bonos M Diciembre 2007 y Junio 2011, se
consideró al bono M Diciembre 2024 como un bono representativo en condiciones de mercado "normales" y para el cual se determinan los factores de
ajuste como a continuación se especifica.
35
Valor de F* para una concentración mayor o igual al 50%
Nivel de Confianza del 99%
Valor de F*
1.3
1.25
1.2
1.15
0
0.1
0.2
0.3
0.4
0.5
0.6
Valor de δ
0.7
0.8
0.9
1
Fig. 2.7: Bono Diciembre 2024. Gráfica de F ∗ con respecto a δ, α = 99%.
2.5.1
Bono M Diciembre 2024
Aplicando el mismo procedimiento utilizado para los casos de los bonos M
Diciembre 2007 y Junio 2011, se obtuvieron los factores de ajuste para el bono
M Diciembre 2024, considererando distintos valores de δ y un nivel de confianza α = 99%. Sin embargo, dada la muy baja concentración del bono, no
es necesario tomar distintos rangos de concentración como en los casos anteriores. El resultado del cálculo se muestra en la Figura 2.7.
Obsérvese que para el nivel de confianza del considerado, el factor de
ajuste es mayor a uno para cualquier valor de δ. Esto se debe a que la distribución de pérdidas para el bono M Diciembre 2024 no es normal.
2.5.2
Factor de Distorsión del bono M Diciembre 2007
A partir de la relación (2.20) y utilizando los factores calculados en las secciones 2.4.1 y 2.5.1, se determinaron los factores de distorsión del bono M
Diciembre 2007 para distintos valores de δ y rangos de concentración mínima.
Dichos factores se muestran en la Figura 2.8.
2.6
Otras variables de referencia
Aunque un alto nivel de concentración en la tenencia de la emisión de un
título en particular genera condiciones propicias para la distorsión del precio
del mismo, no necesariamente se sigue que dicha distorsión se de, o bien que
36
1.3
Cociente de F*Dic07/F*Dic24 para distintos niveles de concentración
Nivel de Confianza del 99%
Factor de Distorsión
Factor de Distorsión
Cociente de F*Dic07/F*Dic24 para distintos niveles de concentración
Nivel de Confianza del 95%
1.2
1.1
1
0.9
0.9
1.3
1.25
1.2
1.15
1.1
0.9
0.8
0.7
0.6
Rango de Concentración
0.5
0
0.2
0.4
0.6
Valor de δ
0.8
1
0.8
0.7
0.6
Rango de Concentración
(a) α = 95%
0.5
0
0.2
0.4
0.6
0.8
1
Valor de δ
(b) α = 99%
∗ ) para distintos niveles de concentración
Fig. 2.8: Factor de distorsión (F D
mínima.
la volatilidad de su precio sea significativamente menor que la observada para
otras emisiones del mismo título que no se encuentran concentradas.
Por lo tanto, con el afán de medir de forma más directa el impacto de la
distorsión de los precios del instrumento sobre el factor de ajuste, se consideró
de interés aplicar el Modelo (2.1) a otra variable de referencia. A saber, la
diferencia relativa ( DR) entre los precios observados ( POBS ) y los teóricos
( PTEO ), definida como
P
− PTEO
(2.21)
DR = OBS
PTEO
donde el precio teórico del instrumento se obtiene a partir de algún modelo económetrico ya sea de precios del instrumento o de sus rendimientos
a vencimiento. En este caso en particular, se utilizó el modelo de Nelson &
Siegel (1987), con la modificación de Svensson (1994), el cual modela los rendimientos teóricos del instrumento mediante una regresión no lineal de los
rendimientos a vencimiento de un conjunto de bonos comparables5 . La forma
parámetrica del modelo para la tasa spot rm es:


1 − exp − τm
m
1


rm = β 0 + ( β 1 + β 2 )
− β 2 exp −
+
m
τ1
τ1
!
1 − exp(− τm2 )
m
β3
− β 3 exp −
(2.22)
m
τ2
τ2
Nótese que el modelo de regresión es no lineal debido a los parámetros τ1
y τ2 , por lo que generalmente se fijan primero y se obtienen el resto de los
5 Nelson
& Siegel (1987) proponen por ejemplo usar el modelo para ajustar una curva de bonos
gubernamentales cupón cero, específicamente los T-bills.
37
Valor de F* para distintos niveles de diferenciales
Nivel de Confianza del 99%
Valor del Factor de Ajuste Óptimo F*
Valor del Factor de Ajuste Óptimo F*
Valor de F* para distintos niveles de diferenciales
Nivel de Confianza del 95%
1.6
1.4
1.2
1
0.8
0.08
1
0.07
0.6
0.06
Rango de Diferenciales
1.7
1.6
1.5
1.4
1.3
0.08
1
0.07
0.8
0.2
0
Valor de δ
0.6
0.06
0.4
0.05
1.8
Rango de Diferenciales
(a) α = 95%
0.8
0.4
0.05
0.2
0
Valor de δ
(b) α = 99%
Fig. 2.9: Bono Diciembre 2007. Factor F ∗ para distintos niveles de diferenciales mínimos.
parámetros por mínimos cuadrados ordinarios, repitiéndose el proceso para
distintos valores de τ1 y τ2 . Una vez obtenidos los rendimientos teóricos
a través de (2.22) por medio del proceso descrito anteriormente, es posible
calcular los precios teóricos del instrumento, con lo que se obtiene a su vez
los diferenciales relativos dados por (2.21). En la Figura 2.9 se muestran los
resultados para el bono Diciembre 2007.
2.7
2.7.1
Aplicación de la Teoría de Valores Extremos
Dificultades en la estimación del VaR y CVaR
Típicamente, el VaR y el CVaR se estiman utilizando la distribución empírica
construida a partir de los datos observados. Por lo tanto, bajo estas circunstancias, siempre es posible encontrar un nivel de confianza α suficientemente
cercano al 100% tal que el VaR y el CVaR coincidan para niveles de confianza
mayores o iguales a α en la pérdida máxima registrada. Este hecho, en el caso
de contar con relativamente pocos datos y considerando que la distribución
de pérdidas verdadera es no acotada (e.g. normal), implica que para niveles
de confianza relativamente altos se subestime el riesgo en términos del VaR y
CVaR.
Esta última observación es particularmente relevante en el contexto de
aplicación del análisis realizado ya que a medida que se incrementa el valor
de la variable de referencia (e.g. concentración) se reduce la cantidad de observaciones correspondientes.
De manera sinóptica, las dificultades anteriores se describen de manera
esquemática en la Figura 2.10.
38
↑ Nivel de la variable
↓ Número de Observaciones Consideradas (N)
de referencia (c)
VaRα → CVaRα → Máxima Pérdida
↑ Nivel de Confianza (α)
F* no es creciente respecto a δ
(Condición (2.7))
Subestimación del Riesgo
Fig. 2.10: Dificultades en la estimación del VaR y CVaR.
Para ilustrar la problemática antes descrita, considérese el caso de las pérdidas asociadas a una concentración mayor o igual al 50% para el Bono M
Diciembre 2007. Dado que la muestra contiene 501 datos, para percentiles
superiores al 99.8%, se tendrá que el VaR, el CVaR y la máxima pérdida son
iguales a 0.3301%, como se puede ver a partir de la Tabla 2.2.
Tab. 2.2: Pérdidas asociadas a una concentración mayor o igual a 50%.
Percentil
Pérdidas
99.20%
99.40%
99.60%
99.80%
100%
0.1881%
0.1907%
0.1951%
0.1962%
0.3301%
Debido a las dificultades de estimación anteriormente mencionadas, es
de interés práctico encontrar una metodología que permita remediar parcial
o totalmente dichas dificultades. Dado que la Teoría de Valores Extremos
estudia precisamente el comportamiento de valores extremos, que conlleva al
uso de muestras reducidas, los estimadores obtenidos mediante esta teoría
son candidatos naturales para resolver estos problemas.
39
2.7.2
Estimadores del VaR y CVaR usando TVE
A partir de la Teoría de Valores Extremos, McNeil (1999) deriva los estimadores del VaR y CVaR
[α = u + β̂
VaR
ξ̂
n
(1 − α )
Nu
!
−ξ̂
−1
[
\α = VaRα + β̂ − ξ̂u
CVaR
1 − ξ̂
1 − ξ̂
(2.23)
(2.24)
donde n es el número total de datos, Nu es el número de datos que exceden el
umbral u; y ξ̂, β̂ son los estimadores de los parámetros ξ y β de la distribución
Pareto Generalizada dada por
(
−1
1 − (1 + ξx/β) ξ para ξ 6= 0,
Gξ,β ( x ) =
(2.25)
1 − exp(− x/β)
para ξ = 0.
donde β > 0, y x ≥ 0 cuando ξ ≥ 0 y 0 ≤ x ≤ − β/ξ si ξ < 0.
La derivación de los estimadores (2.23) y (2.24) se lleva acabo a partir de
la relación
F ( x ) = (1 − F (u)) Fu ( x − u) + F (u)
(2.26)
Fu (y) = P( X − u ≤ y| X > u)
(2.27)
donde
es la distribución de los excesos sobre el umbral u, para 0 ≤ y ≤ x F − u,
y donde x F es el extremo derecho de la distribución F, definido como x F =
sup{ x ∈ R| F ( x ) < 1}. Por el teorema de Pickands-Balkema-de Haan6 la distribución de excesos Fu se puede aproximar por una distribución Pareto Generalizada con parámetros ξ y β, para un umbral u "suficientemente grande".
Es decir,
Fu (y) ≈ Gξ,β (y)
(2.28)
para u suficientemente grande. Por lo tanto,
F ( x ) ≈ (1 − F (u)) Gξ,β ( x − u) + F (u)
(2.29)
para x > u. Luego entonces, estimando F (u) con
n − Nu
n
6 Ver
Teorema 1.2.
40
(2.30)
donde Nu es el número de datos que exceden el umbral u, se deduce que
F̂ ( x ) = 1 −
Nu
n
1 + ξ̂
x−u
β̂
− 1
ξ̂
(2.31)
Así, para obtener la aproximación del VaRα basta usar la definición F̂ (VaRα ) =
α y despejar el VaR usando (2.31). Para obtener la aproximación (2.24) del
CVaRα , se parte de la Proposición 1.6 para obtener la identidad
CVaRα = VaRα + E[ X − VaRα | X > VaRα ]
(2.32)
demostrada en la Proposición 1.6, de la relación
E[ X − VaR | X > VaR] = E[ Z ]
(2.33)
donde Z ∼ FVaRα , y de la aproximación
FVaRα (y) ≈ Gξ (VaRα −u),β (y)
para deducir que
E[ X − VaRα | X > VaRα ] ≈
β + ξ (VaRα −u)
1−ξ
(2.34)
Por lo tanto, de (2.34) y (2.32) se obtiene (2.24).
2.7.3
Aplicación en la determinación de F ∗
Con el fin de mitigar las dificultades en la estimación del VaR y CVaR se obtuvo el factor de ajuste F ∗ aplicando TVE . Para ello se siguieron los siguientes
pasos:
1. Se filtraron los datos respecto al nivel de concentración.
2. A partir de los datos obtenidos, y dado un nivel de confianza α, se
escogió el umbral u tomando u = VaRα .
3. Una vez determindo el umbral se estimaron los parámetros de la distribución Pareto Generalizada.
4. A partir de la estimación anterior de los parámetros, se obtuvieron los
estimadores del VaR dado por (2.23) y del CVaR dado por (2.24).
5. Con los estimadores del VaR y CVaR se obtuvo el Factor de Ajuste para
distintos valores de δ y niveles de la variable de referencia.
41
Fig. 2.11: Factor de Ajuste para distintos niveles de concentración.
Utilizando los datos de rendimientos del Bono M Diciembre 2007, se instrumentó el procedimiento anterior para un nivel de confianza del 95%, considerando distintos rangos de concentración. Los resultados se muestran en
la Figura 2.11. Como puede apreciarse de dicha figura, la estimación del factor
de ajuste F ∗ es muy similar a la obtenida con anterioridad.
Aunque el procedimiento anterior puede ser automatizado fácilmente, no
garantiza que el umbral escogido sea el adecuado y por ende que la estimación lo sea. Como alternativa para determinar el umbral puede utilizarse el
siguiente procedimiento, propuesto por Sarma (2005), que consiste a grandes
rasgos en lo siguiente:
1. Hacer un análisis exploratorio de los datos, con el fin de verificar si existe
una cierta estructura de dependencia en el tiempo de las observaciones
(e.g. evidencia de autocorrelación).
2. Si hay indicación de dependencia, especificar un modelo de series de
tiempo adecuado. En el caso de series financieras podría utilizarse un
modelo GARCH.
3. Si el modelo anterior está bien especificado, los residuos obtenidos deberán ser variables aleatorias independientes e idénticamente distribuidas. Por ende, por el Teorema de Pickands-Balkema-de Haan, para un
umbral suficientemente grande, la cola de la distribución de los residuos
podrá ser modelada a través de una distribución Pareto Generalizada.
4. Ajustar la distribución Pareto Generalizada para varios umbrales. Los
umbrales pueden ser escogidos de tal forma que representen el 1%, 2%,
3%, ..., hasta el 15% de las observaciones extremas. Graficar los parámetros estimados, y a partir de la gráfica escoger un umbral para el cual la
estimación de los parámetros sea relativamente estable.
42
5. Aplicar una prueba de bondad de ajuste para evaluar que tan significativa es la diferencia entre la cola de la distribución empírica y la cola
estimada mediante la distribución Pareto Generalizada. Para ello podría
utilizarse, por ejemplo, la prueba de Kolmogorov-Smirnoff (KS).
Aunque el ajuste de los datos observados a partir de un modelo GARCH
se encuentra más alla del alcance del presente trabajo, el lector interesado
puede consultar el trabajo de Sarma (2005) para una exposición más detallada
del procedimiento antes delineado.
2.8
Conclusiones
La motivación principal de este capítulo fue determinar el "ajuste adecuado"
que debe aplicarse a la desviación estándar de las pérdidas para estimar el
riesgo de mercado de manera más precisa, bajo condiciones de distorsión de
los precios.
De esta manera, se adoptó un criterio para definir lo que se entendería
por "ajuste adecuado". A saber, en términos de la determinación de un factor
de ajuste que al multiplicarse por la desviación estándar observada, dé como
resultado una desviación estándar ajustada con base en la cual se estiman simultáneamente el VaR y el CVaR, de la manera "más precisa posible". Es decir,
de manera tal que el VaR y CVaR estimados, utilizando la desviación estándar
ajustada, se parezca lo "más posible" al VaR y CVaR observados. Concretamente, que la desviación cuadrática de los valores estimados y observados de
estas medidas de riesgo sea mínima.
El criterio anterior se formuló matemáticamente como la solución de un
problema de optimización que presenta las siguientes ventajas:
• La formulación permite asignar el peso relativo que tiene la desviación
cuadrática relacionada con el CVaR respecto a aquélla vinculada con el
VaR. El valor de dicho peso relativo, denominado δ, se puede asociar,
al menos intuitivamente, a un cierto nivel de aversión al riesgo en el sentido de que entre mayor sea el valor de este ponderador, mayor es la
importancia se le da al valor estimado del CVaR, la medida de riesgo
más conservadora de las dos consideradas en el presente análisis.
• El problema de optimización tiene solución explícita y única, lo cual
implica lo siguiente:
– Existe una fórmula explícita para el factor de ajuste.
– El factor de ajuste está caracterizado por dicho problema de optimización.
• El factor de ajuste caracterizado de esta manera tiene propiedades teóricas atractivas. Por ejemplo:
43
– Es igual a uno para el caso en que la distribución de pérdidas sea
una distribución normal. Es decir, en caso de que el supuesto estándar de la distribución de pérdidas se cumpla en la realidad, no
hay ajuste que hacer a la desviación estándar observada. Esto implica que en la forma en que se caracteriza el factor de ajuste, no
existe ningún sesgo bajo el supuesto estándar de la distribución de
pérdidas.
– Es mayor o igual que cero para niveles de confianza mayores o
iguales al 50%, en los que el VaR observado es mayor o igual que
la pérdida promedio; condiciones que típicamente se cumplen en
la práctica.
– Es una función creciente del ponderador δ, es decir, el factor de
ajuste aumenta conforme el nivel de aversión al riesgo se incrementa, bajo las siguientes dos condiciones:
∗ El VaR observado es mayor que la pérdida promedio.
∗ La pérdida en exceso, respecto a la pérdida promedio, asociada
con el CVaR es mayor que la correspondiente pérdida en exceso
relacionada con el VaR en una proporción mayor o igual a la
proporción en que el CVaR es mayor al VaR de una distribución
normal estándar.
Ambas condiciones se cumplen típicamente en la práctica. La primera debido a que usualmente la medición del VaR se hace para
niveles de confianza superiores al 95%, para los cuales el VaR observado es mayor que la pérdida promedio. La segunda, dado que
la distribución de las pérdidas en la práctica por lo general tiene
colas pesadas.
En el contexto particular en el que se aplicó la metodología desarrollada se
obtuvieron los siguientes resultados:
• Para el caso del Bono M Diciembre 2007, se obtuvieron los factores de
ajuste considerando dos niveles de confianza, 95% y 99%, para cada uno
de los cuales se tomaron en cuenta distintos niveles de concentración,
variando el nivel de aversión al riesgo del 0% al 100%. Para dichos
factores se observa lo siguiente:
– El rango de los factores de ajuste es [0.92, 1.4], para α = 95%, y de
[1.38, 1.67], para α = 99%.
– Para cualquier nivel de concentración considerado se cumple que
los factores de ajuste aumentan conforme el nivel de aversión al
riesgo se incrementa.
44
• Para el caso del Bono M Junio 2011, el rango de los factores de ajuste
para α=99% es [2.08,2.51]. En este caso los factores de ajuste disminuyen
conforme se incrementa el nivel de aversión al riesgo para cualquier
nivel de concentración considerando.
• Para el caso del Bono M Diciembre 2024, el rango de los factores de
ajuste es [1.17,1.29]. En este caso los factores de ajuste se incrementan
conforme el nivel de aversión al riesgo se incrementa.
• Utilizando los resultados del Bono M Diciembre 2024, se aisló el efecto
de distorsión de los precios del Bono M Diciembre 2007, en términos de
factores de distorsión para los que se observa lo siguiente:
– En general el valor de los factores disminuyen para cualquier nivel
de concentración considerado, respecto al valor de los factores sin
considerar el Bono M Diciembre 2024.
– Considerando un nivel de confianza del 95% los factores de ajuste
se incrementam conforme se incrementa el nivel de aversión al
riesgo para cualquier nivel de concentración considerando.
– Considerando un nivel de confianza del 99% los factores de ajuste
se incrementan conforme se incrementa el nivel de aversión al riesgo
para niveles de concentración superiores al 77% y disminuyen conforme se incrementa el nivel de aversión al riesgo para niveles de
concentración inferiores al 77%.
La metodología desarrollada en este capítulo se puede adaptar fácilmente
para
• Añadir o incluir otras medidas de riesgo distintas al VaR y CVaR.
• Incorporar restricciones adicionales sobre el factor de ajuste.
• Utilizar otras variables de referencia.
45
Capítulo 3
Aplicación de Distribuciones
Híbridas
3.1
Introducción y Motivación
En el capítulo anterior se desarrolla y ejemplifica la aplicación de una metodología para ajustar el parámetro de desviación estándar con el objeto de medir
el riesgo de mercado -en términos del VaR y del CVaR- de manera más precisa
en condiciones de distorsión de los precios, bajo el supuesto estándar de que
los rendimientos de los mismos se distribuyen de acuerdo a una distribución
Gaussiana.
En este capítulo, al igual que el anterior, se busca medir dicho riesgo partiendo del supuesto estándar de una distribución de pérdidas Gaussiana. Sin
embargo, en lugar de ajustar el parámetro de desviación estándar, se incorpora la posibilidad de realización de un evento de estrés en el cual la distribución de pérdidas es distinta a la distribución Gaussiana que es considerada
bajo condiciones normales. De esta manera, lo que se busca es determinar
la verosimilitud de dicho evento de estrés la cual, junto con la distribución
de pérdidas considerada en este evento, permite construir una distribución
"híbrida" a partir de la cual se mide el riesgo de manera más precisa. Por lo
tanto, el objetivo central de este capítulo es describir una metodología para
determinar dicha distribución "híbrida".
Este capítulo se encuentra organizado de la siguiente manera: en la Sección 3.2 se define, de manera formal, e ilustra el concepto de distribuciones
de probabilidad híbridas. En la Sección 3.3 se formula matemáticamente el
modelo para la determinación de la probabilidad de condiciones de estrés,
la cual se utiliza para establecer la distribución de pérdidas híbrida. En la
Sección 3.4 se estudian algunas propiedades teóricas de la probabilidad de
estrés obtenida a través de dicho modelo. En la Sección 3.5 se describe la
46
instrumentación del modelo para la obtención de la probabilidad de estrés
mediante la aplicación de simulación. En las Secciones 3.6 y 3.7 se aplica la
metodología desarrollada en el contexto de los bonos que motivaron este trabajo de tesis. A saber, se desarrollan dos casos particulares de distribuciones
híbridas considerando, en ambos casos, una distribución Gausssiana para las
condiciones normales y una Gaussiana y una t de Student, respectivamente,
para las condiciones de estrés. Finalmente en la Sección 3.8 se concluye.
3.2
Distribuciones Híbridas
De manera formal, la distribución híbrida asociada a dos distribuciones es
la distribución no condicional correspondiente a dichas distribuciones, suponiendo que éstas son distribuciones condicionales de eventos complementarios. En términos matemáticos,
Definición 3.1 (Distribución Híbrida). Sea X una variable aleatoria tal que
X ∼ FA si el evento A ocurre y X ∼ FB si el evento B ocurre, donde A y B son
conjuntos complementarios. Entonces la distribución híbrida FH de FA y FB
satisface
FH ( x ) = βFA ( x ) + (1 − β) FB ( x )
(3.1)
para toda x ∈ Rango( X ), donde P[ A] = β.
Las distribuciones híbridas surgen de manera natural en el contexto de
riesgos cuando es necesario medir el riesgo en dos circunstancias mutuamente
excluyentes cuyas distribuciones son típicamente muy diferentes. Para ilustrar el concepto y la aplicación de distribuciones híbridas considerénse los
siguientes ejemplos:
Ejemplo 3.1 (Pérdidas por Riesgo de Crédito). Una institución financiera desea medir sus pérdidas por riesgo de crédito. Para ello, la institución estima
que dichas pérdidas, en términos relativos, y las cuales se denotan por Π,
ascienden a un porcentaje M, en caso de incumplimiento de sus deudores con
probabilidad p, y a cero en caso contrario con probabilidad 1 − p. Dicho porcentaje M se comporta de acuerdo a una distribución triangular Λ(·| a, υ, b),
donde a > 0 es el valor mínimo, υ es la moda y b su valor máximo; y cuya
función de densidad (Figura 3.1) es

2( x − a )

para
a≤x<υ

 (b− a)(υ− a)
2
(
b
−
x
)
Λ( x | a, υ, b) =
(3.2)
para
υ≤x<b
(b− a)(b−υ)


 0
en otro caso
Para medir sus pérdidas, la institución determina la distribución de Π de
la siguiente manera:
47
Fig. 3.1: Función de densidad de la distribución triangular Λ(·| a, υ, b).
Sea I el evento en que los deudores incumplen. Entonces, se cumple
P( Π ≤ x ) = P( I )P( Π ≤ x | I ) + P( I c )P( Π ≤ x | I c )
= pP(Π ≤ x | I ) + (1 − p)P(Π ≤ | I c )
donde
c
P( Π ≤ x | I ) =
0
1
para
para
x<0
x≥0
(3.3)
(3.4)
y
P( Π ≤ x | I ) =

0





para
x<a
para
a≤x<υ





para
para
υ≤x<b
x≥b
( x − a )2
(b− a)(υ− a)
( b − x )2
1 − (b− a)(b−υ)
1
Por lo tanto, de (3.3) a (3.5), se deduce que

0




1− p



( x − a )2
p (b− a)(υ− a) + 1 − p
P( Π ≤ x ) =

2


 1 − p (b−(ba−)(xb)−υ)



1
(3.5)
para x < 0
para 0 ≤ x < a
para
a≤x<υ
para
para
υ≤x<b
x≥b
(3.6)
La institución financiera estima que sus pérdidas relativas pueden variar
desde un valor mínimo de 30% hasta un valor máximo de 70%, con una moda
de 65% y una probabilidad p de 5%. Considerando estos parámetros, se determina la distribución híbrida correspondiente utilizando (3.6) y la cual, junto
con su densidad correspondiente, se ilustran en la Figura 3.2.
Con base en esta distribución híbrida, la institución determina un VaR95% =
0% y un CVaR95% = 55%. Para complementar su análisis, la institución considera otros valores para la probabilidad p, a saber p = 1% y p = 10%. En
la Figura 3.3 se grafican las densidades híbridas correspondientes. El VaR y
48
Función de Distribución Acumulada
de las Pérdidas Π.
Probabilidad de Incumplimiento P=5%
Función de Densidad de las Pérdidas Π.
Probabilidad de Incumplimiento P=5%
1
1
0.95
0.9
0.8
0.8
0.7
0.7
Probabilidad
Probabilidad
0.9
0.6
0.5
0.4
0.6
0.5
0.4
0.3
0.3
0.2
0.2
0.1
0
0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
0
−0.2
1
0
Pérdida en términos relativos
0.2
0.4
0.6
0.8
Pérdida en términos relativos
(a) Función de Densidad
(b) Función de Distribución Acumulada
Fig. 3.2: Densidad y Distribución Híbrida del Ejemplo 3.1.
Función de Densidad de las Pérdidas Π.
Probabilidad de Incumplimiento P=1,5 y 10%
1
P=5%
P=1%
P=10%
0.9
Probabilidad
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Pérdida en términos relativos
Fig. 3.3: Densidad Híbrida para distintas probabilidades de incumplimiento
(Ejemplo 3.1).
CVaR para estas distribuciones híbridas son, respectivamente, VaR95% = 0%,
CVaR95% = 11% y VaR95% = 56.47%, CVaR95% = 62.31%.
Ejemplo 3.2. Considerése la institución financiera del Ejemplo 3.1, pero ahora
dicha institución desea considerar también en su medición de riesgo los rendimientos que obtendría en caso de que sus deudores no incumpliesen. Esto es,
se desea tomar en cuenta tanto el riesgo de crédito como el riesgo de mercado.
Los rendimientos en caso de que no se presenten incumplimientos, según estimaciones de la misma institución, se distribuyen como una distribución normal con media µ = 10% y desviación estándar σ = 3%. Con base en estas
consideraciones, la institución financiera determina la distribución híbrida correspondiente1 la cual, junto con sus marginales, se exhibe en la Figura 3.4.
A partir de dicha distribución híbrida de pérdidas, la institución estima un
VaR95% = 2.59% y un CVaR95% = 54.96%.
1 Para
tal efecto se utilizó simulación, en el apéndice B se describe dicho proceso de simulación.
49
Probabilidad de no
Incumplimiento
Probabilidad de
Incumplimiento
95%
5%
Fig. 3.4: Densidades Marginales y su correspondiente Densidad Híbrida.
Finalmente, antes de terminar esta sección hacemos notar que una variable
aleatoria X con distribución definida de acuerdo a (3.1) se puede expresar de
la forma
X = X A 1 A + XB 1 B
c.s.
(3.7)
donde X A y XB son variables aleatorias tales que X A es independiente de 1 A
y XB es independiente de IB . La equivalencia entre (3.1) y (3.7) se establece en
las siguientes proposiciones.
Proposición 3.1. Sea X una variable aleatoria definida por (3.7), y sea β tal que
P[ A] = β. Entonces la FDA de X, denotada FH , está dada por
FH ( x ) = βFA ( x ) + (1 − β) FB ( x ),
donde FA es la FDA de X A y FB es la FDA de XB .
Demostración.
FH ( x ) = P[{ω ∈ Ω| X (ω ) ≤ x }]
= P[{ω ∈ Ω|( X A 1 A + XB 1 B )(ω ) ≤ x }]
= P[{ω ∈ A ∪ B| X A (ω )1 A (ω ) + XB (ω )1 B (ω ) ≤ x }]
= P[{ω ∈ A|( X A 1 A + XB 1 B )(ω ) ≤ x }]
+ P[{ω ∈ B|( X A 1 A + XB 1 B )(ω ) ≤ x }]
Ahora
P[{ω ∈ A|( X A 1 A + XB 1 B )(ω ) ≤ x }] = P[{ω ∈ A| X A (ω ) ≤ x }]
50
(3.8)
ya que 1 A (ω ) = 1 para toda ω ∈ A y 1 B (ω ) = 0 para toda ω ∈ A. Asimismo
se tiene que
P[{ω ∈ A| X A (ω ) ≤ x }] = P[{ A ∩ {ω ∈ Ω| X A (ω ) ≤ x }]
= P[ A]P[{ω ∈ Ω| X A (ω ) ≤ x }]
= βFA ( x )
donde la penúltima igualdad se sigue de la hipótesis de independencia entre
X A e I A . Análogamente se puede demostrar que
P[{ω ∈ B|( X A 1 A + XB 1 B )(ω ) ≤ x }] = (1 − β) FB ( x ).
Por lo tanto, se concluye que FH ( x ) = βFA ( x ) + (1 − β) FB ( x ).
A continuación se establece el recíproco de la proposición anterior.
Proposición 3.2. Sea X una variable aleatoria cuya FDA, denotada por FH , está
dada por
FH ( x ) = βFA ( x ) + (1 − β) FB ( x ),
donde β = P[ A]. Entonces
X = X A 1 A + XB 1 B
c.s.
donde X A se distribuye de acuerdo a FA y es independiente de 1 A y XB se distribuye
de acuerdo a FB y es independiente de 1 B .
Demostración. Se sigue directamente de la Proposición 3.1 que
X
y
X A 1 A + XB 1 B
tienen la misma FDA, por lo cual, por la Proposición que 1.1
X = X A 1 A + XB 1 B
c.s.
3.3
Formulación Matemática
En términos matemáticos, la distribución híbrida se determina al resolver el
problema de optimización
H ( β) 2
H ( β) 2
Min (1 − δ) VaRαE − VaRα
+ δ CVaRαE − CVaRα
β∈[0,1]
(3.9)
donde β ∈ [0, 1] es la probabilidad con la que las pérdidas se distribuyen
H ( β)
de acuerdo a la distribución en condiciones de estrés; y VaRα
51
H ( β)
y CVaRα
1− β
β
Probabilidad de
Estrés ( β)
Se minimiza la distancia
entre VaRH (CVaRH) y
VaRE (CVaRE)
Fig. 3.5: Ajuste de la distribución híbrida por medio del Modelo 3.9.
denotan, respectivamente, el VaR y CVaR de la distribución híbrida asociada
a la probabilidad β. El proceso de determinación de la distribución híbrida
mediante la solución del problema (3.9) es esquematizado en la Figura 3.5.
Obsérvese que, en esencia, el problema (3.9) es el mismo que el problema (2.1), formulado para obtener el factor de ajuste óptimo. La diferencia
estriba en que en un caso, el del problema (2.1), se supone que la distribución
de pérdidas es normal mientras que en el otro caso, el del problema (3.9),
se considera que dicha distribución de pérdidas es una distribución híbrida
proveniente de dos distribuciones predeterminadas.
En contraste con (2.1), en el caso del problema (3.9) no existe una solución
H ( β)
explícita. La razón principal de ello radica en que, en general, el VaRα
y el
H ( β)
CVaRα
no pueden expresarse como funciones explícitas de la probabilidad
β. Por lo tanto, el problema (3.9) debe ser típicamente resuelto de manera
numérica y la derivación de propiedades teóricas generales sobre la probabilidad óptima β∗ es más difícil que en el caso del factor de ajuste óptimo
F ∗ , tratado en el capítulo anterior. No obstante dicha dificultad se derivan
algunas propiedades generales en la siguiente sección.
3.4
H ( β)
Propiedades del VaRα
H ( β)
, CVaRα
y β∗
En esta sección se estudian propiedades sobre el VaR y el CVaR determinados
a partir de una distribución híbrida, así como de la probabilidad de estrés
52
óptima β∗ obtenida al resolver (3.9). A saber, las siguientes:
• La relación del VaR de la distribución híbrida de pérdidas con los correspondientes valores de las distribuciones de pérdidas en condiciones
de normales y condiciones de estrés.
H ( β)
• Condiciones suficientes para la continuidad y monotonicidad del VaRα
y
H ( β)
CVaRα
como función de la probabilidad de estrés β.
• Condiciones suficientes para la existencia de una probabilidad de estrés
óptima β∗ .
Para establecer las propiedades anteriores, es conveniente denotar por N
y CE a los eventos en que las pérdidas Π se comporten en condiciones normales y condiciones de estrés, respectivamente. De esta manera, la distribución híbrida considerada H ( β) para las pérdidas Π implica, por las Proposiciones 3.1 y 3.2 , que éstas se pueden expresar como
Π = Π N 1 N + ΠCE 1CE
c.s.
donde Π N y ΠCE son las pérdidas en condiciones normales y en condiciones
de estrés, respectivamente; 1 N y 1CE son variables indicadores de los eventos
N y CE, respectivamente, y donde se cumple que P[CE] = β. Las funciones
de distribución acumulada de Π N y ΠCE serán denotadas FN y FCE respectivamente.
3.4.1
Propiedades Básicas
Proposición 3.3. Supóngase que Π N y ΠCE son variables aleatorias continuas y que
VaRα (Π N ) ≤ VaRα (ΠCE ). Entonces,
H ( β)
VaRα (Π N ) ≤ VaRα
≤ VaRα (ΠCE )
para toda β ∈ [0, 1].
Demostración.
H ( β)
FH (VaRα
)=α
= βα + (1 − β)α
= β FCE (VaRα (ΠCE )) + (1 − β) FN (VaRα (Π N ))
≤ β FCE (VaRα (ΠCE )) + (1 − β) FN (VaRα (ΠCE ))
= FH (VaRα (ΠCE )).
Por lo tanto,
H ( β)
FH (VaRα
) ≤ FH (VaRα (ΠCE )),
53
lo cual implica, por lo monotonía de FH , que
H ( β)
VaRα
≤ VaRα (ΠCE ).
H ( β)
De manera análoga se demuestra que VaRα (Π N ) ≤ VaRα
.
Corolario 3.1. Supóngase que Π N y ΠCE son variables
aleatorias
continuas, y que
H ( β) −∞ < VaRα (Π N ) ≤ VaRα (ΠCE ) < ∞, entonces VaRα < ∞ para toda β ∈
[0, 1].
H ( β)
≤ VaRα (ΠCE ) para
< ∞ y de manera similar se demuestra que
Demostración. Por la Proposición 3.3 se tiene que VaRα
toda β ∈ [0, 1] por lo que
H ( β)
−∞ < VaRα
3.4.2
.
H ( β)
VaRα
H ( β)
Monotonicidad y Continuidad del VaRα
H ( β)
y CVaRα
H ( β)
H ( β)
Para demostrar la monotonicidad y continuidad del VaRα
y CVaRα
se
hace uso del concepto de dominancia estocástica que a continuación se define.
Definición 3.2. Sean X y Y dos variables aleatorias que representan las pérdidas de un portafolio, se dice que X domina estocásticamente2 a Y, lo cual se
denota como X Y, si
P [ X > u ] ≤ P [Y > u ] ,
para toda u ∈ R.
(3.10)
En palabras, la definición anterior indica que X domina a Y si y sólo si,
dado un umbral u, la probabibilidad de que X sea mayor a u es menor o
igual a la probabilidad que Y sea mayor a u. En particular, si X y Y denotan
pérdidas financieras, la dominancia estocástica de X sobre Y significa que
dado un umbral de pérdidas u, es más probable que las pérdidas de Y superen
dicho umbral que las pérdidas de X. Es decir, en un contexto de pérdidas, la
dominancia estocástica de X sobre Y captura la idea de que X "es menos
riesgoso" que Y. Esta idea es formalizada en la Proposición 3.4.
Antes de exponer los resultados de esta sección, se presenta el siguiente
lema, que demuestra una caracterización alternativa del concepto de dominancia estocástica anteriormente definido, la cual es útil para demostrar los
resultados que se presentan posteriormente.
Lema 3.1. Sean X y Y dos variables aleatorias. Entonces X Y si y sólo si
FX (u) ≥ FY (u), ∀ u ∈ R.
2 Dentro de la teoría estándar de dominancia estocástica, ésta dominancia es una del tipo de
primer orden. De hecho, obsérvese que la desigualdad en la Definición 3.2 va en sentido inverso
a la definición tradicional, ya que en este caso todo se encuentra en términos de pérdidas.
54
Demostración. Supóngase que X Y. Entonces, por definición se cumple
P[ X > u] ≤ P[Y > u], ∀ u ∈ R,
lo cual se cumple si y sólo si,
1 − P[ X ≤ u] ≤ 1 − P[Y ≤ u], ∀ u ∈ R,
o equivalentemente si,
FX (u) ≡ P[ X ≤ u] ≥ P[Y ≤ u] ≡ FY (u), ∀ u ∈ R.
Proposición 3.4. Sean X y Y variables aleatorias tales que X Y. Entonces
VaRα ( X ) ≤ VaRα (Y ) para toda α ∈ [0, 1].
Demostración. Por el Lema 3.1 si X Y, entonces
FX (u) ≥ FY (u), ∀ u ∈ R.
Sea α ∈ [0, 1], entonces
FX (u) ≥ α ⇒ FY (u) ≥ α, ∀ α ∈ [0, 1],
de donde
{u ∈ R| FX (u) ≥ α} ⊂ {u ∈ R| FY (u) ≥ α}, ∀ α ∈ [0, 1],
lo cual su vez implica que,
inf{u ∈ R| FX (u) ≥ α} ≤ inf{u ∈ R| FY (u) ≥ α}, ∀ α ∈ [0, 1],
o equivalentemente que,
VaRα ( X ) ≤ VaRα (Y ), ∀ α ∈ [0, 1].
H ( β)
VaRα ).
Proposición 3.5 (Monotonicidad del
Sean FCE y FN funciones estrictamente crecientes, y supóngase que Π N ΠCE . Entonces, para cualquier nivel
H ( β)
de confianza α ∈ [0, 1] predeterminado, se cumple que la función β 7→ VaRα
H ( β)
VaRα
es no decreciente.
Demostración. Obsérvese que basta demostrar que FH ( β) es decreciente en β
para toda x ∈ R, dado que β 1 ≤ β 2 implica que FH ( β1 ) ( x ) ≥ FH ( β2 ) ( x ) para
toda x ∈ R, lo que a su vez implica, por el Lema 3.1 y la Proposción 3.4, que
H ( β1 )
VaRα
H ( β2 )
≤ VaRα
∀ α ∈ [0, 1]. Para demostrar que FH ( β) es decreciente
55
en β, nótese que Π N ΠCE implica, por el Lema 3.1, que FN ( x ) ≥ FCE ( x ), o
equivalentemente, que FCE ( x ) − FN ( x ) ≤ 0. Por lo tanto,
FH ( β) ( x ) = βFCE ( x ) + (1 − β) FN ( x )
= β( FCE ( x ) − FN ( x )) + FN ( x ).
es una función (lineal) decreciente en β, para toda x ∈ R.
H ( β)
Proposición 3.6 (Monotonicidad del CVaRα ). Sean FCE y FN funciones estrictamente crecientes, y supóngase que Π N ΠCE , y
−∞ < VaRα (Π N ) ≤ VaRα (ΠCE ) < ∞.
Entonces, para cualquier nivel de confianza predeterminado α ∈ [0, 1] la función
H ( β)
β 7→ CVaRα
es no decreciente.
Demostración. Antes de demostrar la proposición, se hace la siguiente observación: Dado que Π N ΠCE , se sigue del Lema 3.1 que β 1 ≤ β 2 implica que
FH ( β1 ) ≥ FH ( β2 ) , y por lo tanto
α
FH
(β
1)
=
FH ( β1 ) − α
1−α
≥
FH ( β2 ) − α
1−α
= FHα ( β2 )
(3.11)
α
(z) ≤ 1 − FHα ( β ) (z).
y por ende se tiene que 1 − FH
( β1 )
2
Para demostrar la proposición, nótese que el valor esperado de una variable aleatoria continua con soporte [ L, ∞) y FDA dada por F, puede ser
representado como
E[ X ] = L +
Z ∞
L
[1 − F (z)]dz.
(3.12)
Así tomando L = VaRα ( X ), CVaRα ( X ) puede ser expresado como
CVaRα ( X ) = VaRα ( X ) +
Z ∞
VaRα
[1 − F α (z)]dz
(3.13)
donde F α (z) representa la α − cola de la distribución de pérdidas como definido
H ( β1 )
en la Definición 1.13. Por ende, denotando u1 = VaRα
56
H ( β2 )
y u2 = VaRα
se
sigue que
H ( β1 )
CVaRα
= u1 +
= u1 +
Z ∞h
u1
Z u2
i
α
1 − FH
( β ) ( z ) dz
(3.14)
1
h
u1
Z
i
α
1 − FH
(
z
)
dz
+
(β )
1
∞
u2
h
i
α
1 − FH
(
z
)
dz
(β )
1
Z ∞h
i
α
1 − FH
(
z
)
dz
≤ u1 + ( u2 − u1 ) · 1 +
( β1 )
u2
Z ∞h
i
α
1 − FH
= u2 +
( β 1 ) ( z ) dz
u2
Z ∞h
i
α
1 − FH
(
z
)
dz
≤ u2 +
( β2 )
(3.16)
(3.17)
(3.18)
u2
H ( β2 )
= CVaRα
(3.15)
.
(3.19)
α
(z) ≤
Donde (3.14) se sigue de (3.13), (3.16) se sigue del hecho que 1 − FH
( β1 )
1, (3.18) se sigue de (3.11) y (3.19) se sigue de (3.13).
H ( β)
Proposición 3.7 (Continuidad del VaRα ). Sean FN y FCE funciones estrictamente monótonas y continuas y supóngase Π N ΠCE y que
−∞ < VaRα (Π N ) ≤ VaRα (ΠCE ) < ∞.
H ( β)
Entonces, la función β 7→ VaRα
es continua, para toda α ∈ [0, 1].
Demostración. Sea β ∈ [0, 1] y β n : N → [0, 1] una sucesión que converge al
valor β. Se probará que
H(βn )
lim β n = β ⇒ lim VaRα
n→∞
n→∞
H(βn )
Por el Corolario 3.1 la sucesión VaRα
.
esta acotada y por la Proposición 3.5
H(βn )
es no decreciente, por lo que limn→∞ VaRα
probar que dicho límite es igual a
H ( β)
= VaRα
H ( β)
VaRα .
existe. Por lo tanto basta con
Para tal efecto, obsérvese que
α = lim α
(3.20)
n→∞
H(β )
= lim FH ( β n ) VaRα n
n→∞
h
i
H(β )
H(β )
= lim β n FCE VaRα n + (1 − β n ) FN VaRα n
n→∞
H(β )
H(β )
= β lim FCE VaRα n + (1 − β) lim FN VaRα n
n→∞
n→∞
H(βn )
H(β )
= βFCE lim VaRα
+ (1 − β) FN lim VaRα n
(3.21)
= βFCE ( x ) + (1 − β) FN ( x ∗ ).
(3.25)
n→∞
∗
n→∞
57
(3.22)
(3.23)
(3.24)
H(βn )
donde x ∗ = limn→∞ VaRα
se deduce que
H ( β)
. Sea y∗ = VaRα
, entonces por (3.20) y (3.25),
βFCE ( x ∗ ) + (1 − β) FN ( x ∗ ) = α = βFCE (y∗ ) + (1 − β) FN (y∗ ),
(3.26)
para toda β ∈ [0, 1]. En particular, para β = 1 y β = 0 se obtiene que
FCE ( x ∗ ) = FCE (y∗ )
y
FN ( x ∗ ) = FN (y∗ )
lo cual implica, por la monotonía estricta de FCE y FN , que x ∗ = y∗ , o lo que
H(βn )
H ( β)
= VaRα
es lo mismo, que el limn→∞ VaRα
H ( β)
Para demostrar la continuidad del CVaRα
sultado:
.
se requiere del siguiente re-
Lema 3.2. Si g es una función integrable en R, entonces la función
G (u) =
Z ∞
u
g(z)dz
(3.27)
es continua en u, para toda u ∈ R.
Demostración. Si g es una función integrable en R, se sigue del Teorema 8 del
Capítulo 13 de Spivak (1996) que la sucesión de funciones definidas por
Gn (u) =
Z n
u
g(z)dz
son continuas en u ∈ R, para toda n ∈ N. Dado que
G (u) = lim Gn (u) =
n→∞
Z ∞
u
g(z)dz
(3.28)
Se sigue que
( Z
)
Z n
∞
lim sup{| G (u) − Gn (u)|} = lim sup g(z)dz −
g(z)dz
n → ∞ u ∈R
n → ∞ u ∈R
u
u
Z ∞
g(z)dz
= lim sup n→∞
n
u ∈R
=0
(3.29)
(3.30)
(3.31)
Por lo tanto, Gn (u) converge uniformemente a G (u). Como Gn (u) es continua
para toda u ∈ R y para toda n ∈ N, se sigue que la función G (u) es continua
para toda u ∈ R.
H ( β)
Proposición 3.8 (Continuidad del CVaRα ). Sean FCE y FN funciones estrictamente monótonas y continuas; y supóngase que Π N ΠCE y que
−∞ < VaRα (Π N ) ≤ VaRα (ΠCE ) < ∞.
H ( β)
Entonces, la función β 7→ CVaRα
es continua para toda α ∈ [0, 1].
58
H ( β)
Demostración. De la definición de CVaRα
H ( β)
CVaRα
se sigue que
Z ∞
1
z [ β f CE (z) + (1 − β) f N (z)]dz
(3.32)
1 − α VaRαH (β)
Z ∞
Z ∞
β
1−β
=
z
f
(
z
)
dz
+
z f N (z)dz (3.33)
CE
H ( β)
H ( β)
1−α
1−α
VaRα
VaRα
=
Por el Lema 3.2 se deduce que
GCE (u) ≡
Z ∞
u
z f CE (z)dz
y
GN (u) ≡
Z ∞
u
z f N (z)dz
(3.34)
H ( β)
son continuas en u, para toda u ∈ R. Por lo tanto, dado que VaRα
es una función continua con respecto a β, se concluye que la composición
H ( β)
GN (VaRα
H ( β)
) y GCE (VaRα ) son continuas con respecto a β, de donde se
H ( β)
concluye de (3.33) que el CVaRα
es una función continua con respecto a
β.
3.4.3
Existencia y algunas propiedades de β∗
En la siguiente Proposición se establece la existencia de una solución para el
problema de optimización (3.9). Es decir, se establece la existencia de una
probabilidad óptima de estrés óptima β∗ .
Proposición 3.9. Sean FN y FCE funciones estrictamente monótonas y continuas, y
supóngase Π N ΠCE y que −∞ < VaRα (Π N ) ≤ VaRα (ΠCE ) < ∞. Entonces el
problema de optimización (3.9) tiene solución.
Demostración. Dado que la función objetivo del problema de optimización (3.9)
se puede expresar como
H ( β) 2
H ( β) 2
G ( β) ≡ (1 − δ) VaRαE − VaRα
+ δ CVaRαE − CVaRα
H ( β)
H ( β)
y que las funciones VaRα
y CVaRα
son continuas en β, por las Proposiciones 3.7 y 3.8, se desprende entonces que G ( β) es una función continua, al
ser una composición de funciones continuas. Por lo tanto, dado que la función objetivo G ( β) se minimiza sobre el intervalo [0, 1] el cual es un cojunto
compacto, se concluye que G ( β) alcanza un mínimo en [0, 1] y por ende que
(3.9) tiene solución.
A continuación se establecen dos resultados con respecto a la solución
óptima de (3.9) para dos casos particulares. A saber, para el caso δ = 0, es
decir cuando sólo es de interés ajustar el VaR, y el caso en que el VaR y CVaR
observado coinciden con aquellos derivados en condiciones normales.
59
Proposición 3.10. Supóngase VaRα (ΠCE ) ≥ VaRα (Π N ) y δ = 0. Entonces la
solución óptima de (3.9) es β̃ = 0
Demostración. Por la Proposición 3.3 se cumple que
H ( β)
VaRα (Π N ) ≤ VaRα
≤ VaRα (ΠCE )
para toda β ∈ [0, 1]. Si β = 0 se tiene que
FH ( x ) = 0 · FCE ( x ) + 1 · FN ( x ) = FN ( x )
H ( β)
por lo que VaRα
= VaRα (Π N ), luego entonces β̃ = 0 es un óptimo para (3.9).
Proposición 3.11. Supóngase VaRαE ( X ) = VaRα (Π N ) y CVaRαE ( X ) = CVaRα (Π N ).
Entonces β∗ = 0 es una solución óptima para el problema de optimización (3.9).
Demostración. Obsérvese que
2
2
G (0) = (1 − δ) VaRαE − VaR(Π N ) + δ CVaRαE − CVaR(Π N )
=0
(3.35)
(3.36)
donde la última igualdad es consecuencia de la hipótesis. Por lo tanto, dado
que G ( β) ≥ 0 para toda β ∈ [0, 1], se concluye que β∗ = 0 es un mínimo. Una vez formulada formalmente la determinación de la distribución híbrida
en términos de la probabilidad de crisis β y de haber establecido algunas
propiedades de esta última, se aborda en la siguiente sección la resolución
numérica del problema de optimización (3.9).
3.5
Determinación de la probabilidad óptima β∗
La resolución numérica del problema (3.9) requiere la determinación de
H ( β) 2
H ( β) 2
G ( β) = (1 − δ) VaRαE − VaRα
+ δ CVaRαE − CVaRα
(3.37)
para cada β ∈ [0, 1]. Para ello, es necesario obtener la distribución híbrida
H ( β)
H ( β) y a partir de ésta obtener VaRα
H ( β)
y CVaRα
H ( β)
VaRα
. Dado que no siempre es
H ( β)
posible encontrar fórmulas explicitas para
y CVaRα , se deben estimar sus valores. Para tal efecto, se propone utilizar simulación. Esto debido a
que es fácil de instrumentar y de adaptar para cualquier par de distribuciones
que se consideren para conformar la distribución híbrida. A saber, se genera
una muestra de la distribución híbrida, de tamaño m, a partir de la cual se
60
H ( β)
H ( β)
estiman VaRα
y CVaRα . De esta manera, la función objetivo (3.37) es
aproximada por la función
2
H ( β) 2
d αH ( β) + δ CVaRαE −CVaR
\α
Ĝ ( β) = (1 − δ) VaRαE −VaR
(3.38)
H ( β)
H ( β)
H ( β)
H ( β)
dα
\α
donde VaR
y CVaR
son estimadores de VaRα
y CVaRα
obtenidos
a partir de la muestra generada. Con base en dicha aproximación, se resuelve (3.9), obteniéndose una probabilidad óptima aproximada c
β∗i . Claramente, la precisión de dicho valor depende tanto del tamaño de la muestra
como de la muestra particular generada. Por lo tanto, es natural generar
varias muestras, obtener una probabilidad óptima aproximada para cada una
de ellas y utilizar el promedio de estos valores como un valor aproximado de
la probabilidad de estrés óptima. Por lo tanto, se propone utilizar el siguiente
algoritmo genérico:
I. Se generan n muestras de tamaño m de la distribución híbrida3 .
II. A partir de cada muestra i generada, i = 1 . . . n, se determina Ĝ ( β) y se
resuelve (3.9), obteniéndose el valor óptimo c
β∗i .
III. Se estima la probabilidad óptima β∗ como
1
c
β∗ =
n
n
β∗i
∑c
(3.39)
i =1
Para la determinación de estos valores se hacen las siguientes consideraciones:
• El error en la estimación se mide por medio del error relativo, definido
como
c
β∗ − β∗ ∗
(3.40)
eR ( β ) ≡ β∗ donde β∗ es la probabilidad de estrés óptima que resuelve el problema
de optimización (3.9).
• Si las n muestras son independientes, entonces, dado que por construcción son idénticamente distribuidas, el teorema del límite central implica
c
β∗ − E[ c
β∗ ]
√ i → N (0, 1)
σβc∗ / n
(3.41)
i
donde σβc∗ denota la desviación estándar común pero desconocida de
i
cada c
β∗i ; y N (0, 1) representa una distribución normal estándar.
3 Esta muestra se genera utilizando un vector de valores aleatorios con distribución uniforme,
un vector de valores aleatorios con distribución idéntica a la de condiciones normales y un vector
de valores aleatorios con distribución idéntica a la de condiciones de estrés. La construcción de
la distribución híbrida a partir de estos vectores se especifica en el Apéndice B, Sección B.2.
61
• Reemplazando la desviación estándar poblacional σβc∗ en (3.41) por la
i
desviación estándar muestral
Sn,βc∗
i
1
=
n−1
s
n
∑
i =1
c
β∗i − c
β∗
2
(3.42)
se tiene que
c
β∗ − E[ c
β∗ ]
√ i → t n −1
Sn,βc∗ / n
(3.43)
i
donde tn−1 es una distribución t de Student con n − 1 grados de libertad.
Por tanto, se deduce


c∗
β − E[ c
β∗i ] √ ≤ tn−1,1−θ/2  = 1 − θ.
P
(3.44)
Sn,βc∗i / n donde θ ∈ [0, 1] es el nivel de significancia en la estimación del error
e R ( β ∗ ).
• Obsérvese que
∆(n, θ ) ≡ tn−1,1−θ/2
Sn,βc∗
√ i
n
!
(3.45)
satisface
lim ∆(n, θ ) = 0
n→∞
(3.46)
Por lo tanto, es posible escoger una n suficientemente grande, de forma
tal que
∆(n, θ ) ≤ γ| c
β∗ |
(3.47)
para un valor 0 < γ < 1 predeterminado. Luego entonces de (3.44)
y (3.47) se sigue que
h
i
∗
(3.48)
β∗i ] ≤ ∆(n, θ )
1 − θ = P c
β − E[ c
i
h
∗
∗
≤ P c
β − E[ c
β∗i ] ≤ γ c
β (3.49)
i
h
∗
∗
= P c
β − E[ c
β∗i ] ≤ γ c
β − E[ c
β∗i ] + E[ c
β∗i ]
(3.50)
i
h
∗
∗
≤ P c
β − E[ c
β∗i ] ≤ γ c
β − E[ c
β∗i ] + E[ c
β∗i ]
(3.51)
h
i
∗
= P (1 − γ ) c
β − E[ c
β∗i ] ≤ γ| c
β∗ |
(3.52)
#
"
|c
β∗ − E[ c
β∗i ]|
γ
≤
(3.53)
=P
| β∗ |
1−γ
62
Si E[ c
β∗i ] = β∗ , entonces c
β∗ es un estimador insesgado4 de β∗ y se deduce
por (3.53), que:
"
#
|c
β∗ − β∗ |
γ
P
≤
≥ 1 − θ.
| β∗ |
1−γ
(3.54)
A partir de las consideraciones anteriores, se utiliza el siguiente algoritmo
para estimar la probabilidad óptima β∗ del modelo (3.9), dado un error relativo γ0 y un nivel de confianza 1 − θ.
1. Generar un número incial predeterminado n0 de muestras, de tamaño
m, a partir de las cuales se obtienen las estimaciones c
β∗i , para i = 1 . . . n0 ,
de acuerdo a lo descrito en el inciso II; n := n0 .
2. Calcular c
β∗ , de acuerdo a (3.39), y ∆(n, θ ), de acuerdo a (3.45), a partir
de los valores c
β∗i para i = 1 . . . n.
3. Si
∆(n,θ )
c∗ |
|β
≤
γ0
1+ γ 0
entonces terminar: β∗ es aproximado por el estimador
c
β∗ y
I (γ0 , θ ) = [ c
β∗ (n) − ∆(n, θ ), c
β∗ (n) + ∆(n, θ )]
(3.55)
es un intervalo de confianza de 100(1 − θ )% para β∗ .
En caso contrario, generar otra muestra de tamaño m, n := n + 1 e ir al
paso 2.
3.5.1
Determinación de la Distribución Híbrida
Para construir la distribución híbrida se deben determinar las distribuciones
que se usarán para las condiciones normales y las condiciones de estrés. Para
tal efecto, es natural considerar distribuciones conocidas y estimar sus parámetros con base en datos observados, si es posible, o una opinión experta.
En el problema particular que nos atañe, se consideró una distribución
Gaussiana para el caso de condiciones normales, y una distribución Gaussiana
o t no central para el caso de condiciones de estrés. Los parámetros de dichas
distribuciones se determinaron de la siguiente manera:
Para cada rango de concentración c considerado5 ,
1. Se filtraron los datos de acuerdo al rango de concentración (c) 6 .
4 En
el Apéndice C se discute brevemente el problema del sesgo potencial en la estimación de
β∗ .
rango de concentración es un intervalo de la forma [c0 , ∞).
ejemplo los datos filtrados de acuerdo al rango de concentración [50%, ∞), representan
los datos de rendimientos diarios (en términos de pérdidas) cuya concentración diaria fue mayor
a 50%.
5 Un
6 Por
63
2. Para los datos filtrados se obtuvo una banda superior de las pérdidas,
para el nivel de confianza predeterminado α, especificada por
µ̂c + N−1 (α)σ̂c
(3.56)
donde:
• µ̂c es la media estimada (promedio aritmético) de las pérdidas que
satisfacen la restricción de concentración dada por c y
• σ̂c es la desviación estándar estimada de las pérdidas que satisfacen
la restricción de concentración dada por c.
3. La distribución en el caso de condiciones normales es N (µ̂c , σ̂c ).
4. Los parámetros en condiciones de estrés se determinaron a partir de los
datos (pérdidas) que rebasan la banda superior.
Esta construcción tiene las siguientes ventajas:
• Si la distribución empírica de las pérdidas es Gaussiana, ésta coincidará
con la distribución en casos normales, por lo cual no habrá que hacer
ajuste alguno y la probabilidad de estrés β∗ sera igual a 0.
• Esta construcción hace que el ajuste dado por la probabilidad de β∗ sea
comparable al ajuste dado por F ∗ en el siguiente sentido: un valor de
β∗ = 0 corresponde al caso en que no se ajusta ni el VaR ni el CVaR, que
es equivalente al caso en que F ∗ = 1, y un valor de β∗ > 0 corresponde
al caso en que es necesario ajustar el VaR y el CVaR, como sería el caso
en que F ∗ > 1.
3.6
Caso Gaussiano-Gaussiano
El primer caso particular que se considera es aquél en que tanto la distribución
en condiciones normales como la de estrés son distribuciones Gaussianas. En
este caso, la densidad de la distribución híbrida esta dada por
f H ( β) ( x ) =
√
β
2πσCE
e
− 21
x −µCE
σCE
2
+
1−β
√
2πσN
e
− 12
x −µ N
σN
2
(3.57)
donde β es la probabilidad de ocurrencia del evento de éstres; µCE y σCE son la
media y desviación estándar respectivas de la distribución de los rendimientos
en caso de éstres; y donde µ N y σN son la media y desviación estándar de los
rendimientos bajo condiciones normales.
Es importante enfatizar que el supuesto de normalidad para ambas distribuciones no restringe mucho la forma de la distribución híbrida. En particular, ésta puede ser una distribución bimodal o leptocúrtica. Por ejemplo,
64
si β = 0.6, µCE = −1, σCE = 1, µ N = 2 y σN = 1 se tiene una distribución
bimodal (ver Figura 3.6a). Asimismo, si β = 0.5, µCE = 0, σCE = 1, µ N = 0 y
σN = 9, se tiene una distribución leptocúrtica (ver Figura 3.6b).
Densidad Híbrida combinación
de dos normales
0.25
0.2
0.2
0.15
0.15
Densidad
Densidad
Densidad Híbrida
combinación de dos normales
0.25
0.1
0.05
0
−4
0.1
0.05
−3
−2
−1
0
1
2
3
0
−4
4
−3
−2
−1
x
0
1
2
3
4
x
(a) Densidad Bimodal
(b) Densidad Leptocúrtica
Fig. 3.6: Densidades híbridas combinación de dos normales.
3.6.1
Solución utilizando simulación
Se resolvió el problema de optimización (3.9) bajo el supuesto de que las pérdidas se distribuyen de acuerdo a la densidad (3.57), utilizando los rendimientos diarios de los precios limpios para el bono M Diciembre 2007, tomando
distintos niveles de concentración y de aversión al riesgo. Para tal efecto, se
utilizó el algoritmo de simulación descrito en la Sección 3.5, considerando los
siguientes parámetros: error relativo γ = 1%, n0 = 10, m = 10, 000. El primer
parámetro fue determinado con base en un nivel de precisión deseado, mientras que el segundo fue definido de manera arbitraria. Por su parte, para
determinar el valor de m se hicieron las siguientes consideraciones:
• Se determinó la distribución empírica de c
β∗i para distintos valores de m
y δ. A saber para los casos m =2’000, 5’000, 10’000 y 20’000; y δ=0, 0.5 y
1. Por ejemplo, en la Figura 3.7 se ilustran las densidades para el caso
particular de δ = 0.5 y α = 0.95 7 .
• En las distribuciones estimadas en el inciso anterior, se determinó el
mínimo valor de m, tal que la desviación estándar de la distribución
fuese menor o igual al 10% del valor de la media de la misma, para
todas las δ’s consideradas. Dicho valor es m = 10, 000.
7 Las distribuciones empíricas fueron obtenidas resolviendo el problema de optimizacion (3.9)
n=10,000 veces. Se puede notar que la dispersión de la distribución de las c
β∗i disminuye y que
valor de su media respectiva se reduce conforme aumenta el valor de m. Este efecto se debe,
H ( β)
presumiblemente, al sesgo en la estimación de VaRα
65
H ( β)
y CVaRα
.
Distribución Empírica de β , para distintos valores de m.
i
δ = 0.5, α = 95%
m=5000
m=10000
m=2000
m=20000
200
180
160
Densidad
140
120
100
80
60
40
20
0
0.01
0.015
0.02
0.025
0.03
0.035
0.04
Beta
Fig. 3.7: Distribución Empírica de c
β∗i para distintos valores de m.
En la Figura 3.8 se muestran las probabilidades óptimas β∗ obtenidas para
distintas combinaciones de aversión al riesgo (δ) y rangos de concentración,
considerando un nivel de confianza α del 95%. A partir de los resultados
obtenidos se hacen las siguientes observaciones:
• Las probabilidades de estrés varían entre valores muy cercanos al 0%,
asociados con δ = 0, y valores ligeramente menores al 4%, asociados con
δ = 100%.
• El valor de β∗ se incrementa conforme aumenta el parámetro de aversión
al riesgo δ. Es decir, entre mayor sea la ponderación que se le da al CVaR,
mayor es la probabilidad de estrés requerida para ajustar el riesgo.
• En general, no hay un efecto claramente discernible de la concentración
sobre el valor de la probabilidad de estrés óptima β∗ . Sin embargo, se
observa que a mayor nivel de concentración, mayor es en promedio la
probabilidad β∗ .
Finalmente, a fin de ilustrar el requerimento computacional del algoritmo,
se presenta en la Figura 3.9 el número de muestras generadas para la obtención de β∗ . En particular, se observa claramente que el número de simulaciones requiridas cuando δ = 0 es considerablemente mayor al resto de los
casos. Esto se debe a que la probabilidad de estrés es muy cercana a 0 y por
lo tanto, el error relativo en la estimación tiende a ser relativamente grande.
3.6.2
Solución mediante integración numérica
En la Sección 3.5 se señala que, en general, es difícil obtener una expresión
H ( β)
explícita del VaRα
H ( β)
y CVaRα
, y por lo tanto, de la función objetivo del
66
Valor de β* para distintos niveles de concentración
Nivel de Confianza del 95%
Probabilidad de Éstres β
0.04
0.03
0.02
0.01
0
0.9
0.8
1
0.7
0.6
0.5
Rango de Concentración
0.8
0.4
0.6
0.2
0
Valor de δ
Fig. 3.8: Gráfica de β∗ para distintos niveles de concentración mínima.
Número de muestras generadas
Nivel de Confianza del 95%
5
No de muestras generadas
x 10
2
1.5
1
0.5
0
0.9
0.8
0.7
0.6
Rango de Concentración
0.5
0
0.2
0.4
0.6
0.8
1
Valor de δ
Fig. 3.9: Número de muestras generadas para obtener c
β∗ .
67
problema (3.9). Sin embargo, para el caso particular que se estudia en esta
sección se pueden obtener fórmulas implícitas, a partir de las cuales es posible obtener una estimación mediante métodos númericos. Dichas fórmulas
implícitas se formulan y demuestran en las siguientes proposiciones.
H ( β)
Proposición 3.12. El VaRα
es solución de la ecuación
u − µN
u − µCE
=α
+ (1 − β ) N
βN
σCE
σN
(3.58)
para u ∈ R.
H ( β)
Demostración. Por definición, si u = VaRα , debe satisfacer
"
2
2 #
Z u x −µ
x −µ
1−β
β
− 12 σ CE
− 21 σ N
N
CE
√
+ √
dx = α
e
e
−∞
2πσCE
2πσN
(3.59)
o, de forma equivalente
β
Z u − 12
e
√
−∞
x −µCE
σCE
2
dx + (1 − β)
2πσCE
Z u − 12
e
−∞
√
2
x −µ N
σN
2πσN
dx = α
(3.60)
simplificando la primera integral de la ecuación (3.60) se obtiene
Z u − 12
e
−∞
√
x −µCE
σCE
2
dx =
2πσCE
u−µCE
σCE
Z
−∞
1 2
e− 2 x
√ dx = N
2π
u − µCE
σCE
(3.61)
Análogamente para la segunda integral de la ecuación (3.60) se obtiene
Z ∞ − 12
e
√
u
x −µ N
σN
2
2πσN
dx = N
u − µN
σN
(3.62)
y, sustituyendo (3.61) y (3.62) en (3.60), se obtiene la ecuación (3.58).
H ( β)
La Proposición 3.12 permite encontrar el VaRα
para una distribución
híbrida, combinación de dos normales, con función de densidad dada por (3.57),
resolviendo la ecuación (3.58) para u. Aunque la ecuación (3.58) no tiene una
H ( β)
solución explícita para el VaRα
, puede ser resuelta por métodos numéricos.
H ( β)
VaRα ,
H ( β)
Una vez obtenido
es posible calcular de forma explícita el CVaRα
como se establece en la siguiente Proposición.
H ( β)
Proposición 3.13. El CVaRα
está dado por
"
1
µCE − u
µN − u
H ( β)
βN
µCE + (1 − β)N
µN
CVaRα
=
1−α
σCE
σN
+
βσCE e
− 12
u−µCE
σCE
68
2
+ (1 − β)σN e
√
2π
− 21
u−µ N
σN
2
#
(3.63)
H ( β)
donde u = VaRα
.
H ( β)
H ( β)
Demostración. Tomando u = VaRα , el CVaRα
estará dado por la expresión
"
2
2 #
Z ∞ x −µ
x −µ
β
1−β
1
− 21 σ N
− 21 σ CE
N
CE
√
+ √
xe
xe
dx (3.64)
1−α u
2πσCE
2πσN
Nótese que la integral de la expresión anterior puede ser escrita como
β
Z ∞ − 12
xe
√
u
x −µCE
σCE
2
dx + (1 − β)
2πσCE
Z ∞ − 21
xe
√
u
x −µ N
σN
2
dx
2πσN
(3.65)
Usando el cambio de variable m(u) = (u − µCE )/σCE en la primera integral
de la expresión anterior, se obtiene que
Z ∞ − 12
xe
√
u
x −µCE
σCE
2πσCE
2
dx =
1 2
Z ∞
m(u)
= σCE
(σCE m + µCE )e− 2 x
√
σCE dm
2πσCE
1
Z ∞
m(u)
Z ∞
m(u)
1
2
e− 2 m
√
dm
2π
(3.67)
2
1
=
2
me− 2 m
√
dm + µCE
2π
(3.66)
σCE e− 2 m(u)
√
+ µCE N(−m(u))
2π
(3.68)
Por lo tanto,
Z ∞ − 12
xe
√
u
x −µCE
σCE
2
2πσCE
dx =
σCE e
− 12
√
u−µCE
σCE
2
+ µCE N
2π
µCE − u
σCE
(3.69)
Analogamente para la segunda integral de la expresión (3.65) se obtiene
Z ∞ − 12
xe
√
u
x −µ N
σN
2πσN
2
dx =
σN e
− 12
√
u−µ N
σN
2π
2
+ µN N
µN − u
σN
(3.70)
Finalmente, sustituyendo (3.69) y (3.70) en (3.65) y multiplicando por
se obtiene (3.63).
1
1− α
Con base en las dos proposiciones anteriores se obtuvo la probabilidad
de estrés óptima β∗ , para mismos niveles de aversión al riesgo y rangos de
concentración considerados en la Subsección 3.6.1. Los resultados se muestran
en la Figura 3.10.
Como se puede observar, los resultados son muy parecidos a aquéllos
obtenidos aplicando el algoritmo de simulación. De hecho, para verificar esto
de manera más precisa, se calcularon las diferencias entre las superficie de
β∗ determinada por simulación β∗sim y aquélla calculada mediante integración
numérica β∗num . Dicha superficie "diferencia" se muestra en la Figura 3.11 y a
partir de ésta se observa lo siguiente:
69
Valor de β* para distintos niveles de concentración
Nivel de Confianza del 95%
Probabilidad de Éstres β
0.04
0.03
0.02
0.01
0
0.9
0.8
1
0.7
0.6
0.6
0.5
Rango de Concentración
0.8
0.4
0.2
0
Valor de δ
Fig. 3.10: Gráfica de β∗ con respecto a δ, para distintos niveles de concentación
mínima y α = 95%.
• Las diferencias son mínimas, ya que su valor máximo es igual a 0.002.
• Las diferencias, en general, son positivas, lo cual indica que la probabilidad de estrés se encuentra consistentemente sobreestimada aplicando
el método de simulación.
• Las mayores diferencias se encuentran para el caso en que δ = 0. Esto se
debe a que la probabilidad de estrés es más cercana a 0, y por ende más
difícil de estimar mediante la simulación, debido a que el error relativo
en la estimación de β∗ es relativamente grande.
Diferencias de β* simulada vs β* por integración numérica,
para distintos niveles de concentración.
Nivel de Confianza del 95%
−3
Diferencias en el cálculo de β*
x 10
3
2
1
0
−1
0.9
0.8
0.7
0.6
Rango de Concentración
0.5
0
0.2
0.4
0.6
0.8
1
Valor de δ
Fig. 3.11: Gráfica de las diferencias de β∗sim − β∗num , para distintos valores de δ
y rangos de concentación, con α = 95%.
70
3.7
Caso Gaussiano-t
El segundo caso particular que se considera es aquél en que la distribución
en condiciones normales es una Gaussiana y la distribución en condiciones
de estrés es una t no central8 . De esta manera, la densidad de la distribución
híbrida en este caso está dada por

2 
x −µ
−( 1+2 ν )
− 12 σ N
2
N
( x − µCE )
e

√
f H ( x ) = βCν 1 +
+ (1 − β ) 
(3.71)
,
φCE ν
σN 2π
donde Cν es una constante de normalización de la distribución t no central
definida como
1
Γ ν+
2
√
.
(3.72)
Cν =
Γ ν2
πφCE ν
µCE es la media de la distibución t no central y φCE es un parámetro de
dispersión que se relaciona con la desviación estándar σCE de la siguiente
manera:
r
p
ν
σCE = φCE
,
(3.73)
ν−2
donde ν es un parámetro relacionado con los grados de libertad de la distribución y el cual se supondrá en lo sucesivo mayor a 2 a fin de que de que
la ecuación (3.73) tenga sentido.
De igual forma que en el caso Gaussiano-Gaussiano, µCE y σCE representan la media y la desviación estándar respectivamente de los rendimientos
en condiciones de estrés, mientras que µ N y σN representan la media y desviación estándar de los rendimientos en condiciones normales. Asimismo, β
representa la probabilidad de estrés.
El caso Gaussiano-t tiene la ventaja de presentar mayor flexibilidad en
la modelación de los rendimientos en condiciones de estrés, dado que, por
una parte, la distribución t permite modelar las colas pesadas y alta curtosis
que regularmente se presentan en las series financieras, y por otra parte la
distribución Gaussiana puede ser considerada un caso particular de la t, ya
que, por el teorema del límite central, la distribución t converge a una normal
cuando el parámetro ν tiende a infinito.
3.7.1
Solución utilizando simulación
Para poder resolver el problema (3.9) en este caso es necesario determinar los
parámetros de la distribución t-no central para las condiciones de estrés. Para
tal efecto, se procedió de la siguiente manera:
8 Ver
Capítulo de Preliminares, sección 1.6
71
1. Se obtuvieron los grados de libertad ν de la distribución, a partir de
la curtosis en exceso estimada de los datos Kν , mediante la relación9
ν = K6ν + 4.
2. Se estimó la desviación estándar de la distribución en condiciones de
estrés a partir de los datos. Usando dicha estimación, se
el
obtuvo
2
2 .
parámetro de dispersión mediante la relación10 φCE = ν−
σ
CE
ν
Con base en las consideraciones anteriores, se resolvió el problema de optimización (3.9) bajo el supuesto (3.71) utilizando los rendimientos diarios del
precio limpio para el bono M Diciembre 2007; y tomando en cuenta distintos
niveles de concentración y de aversión al riesgo. Para tal efecto, y al igual
que en el caso Gaussiano, se utilizó el algoritmo de simulación descrito en la
Sección 3.5, considerando los parámetros de error relativo γ = 1%, n0 = 10
y m = 10, 000. Estos parámetros fueron obtenidos de manera análoga a lo
descrito en la Subsección 3.6.1. Los resultados obtenidos se ilustran en la
Figura 3.12, a partir de la cual se hacen las siguientes observaciones:
• Las probabilidades de estrés obtenidas son muy similares a las del caso
Gaussiano-Gaussiano11 .
• Al igual que en el caso Gaussiano-Gaussiano el valor de β∗ se incrementa
conforme aumenta el parámetro de aversión al riesgo.
• Conforme aumenta la concentración la probabilidad de estrés β∗ aumenta (en promedio).
Asimismo, al igual que se hizo en el caso Gaussiano-Gaussiano, se presenta en la Figura 3.13 el número de muestras generadas para obtener la probabilidad de estrés óptima β∗ en el caso Gaussiano-t. Esto con el fin de visualizar el esfuerzo computacional del algoritmo de simulación. De la misma
manera que en el caso Gaussiano-Gaussiano, el esfuerzo computacional para
δ = 0 es mayor que en el resto de los casos, debido a que la probabilidad de
estrés en dicho caso es muy cercana a cero.
3.7.2
Solución mediante integración numérica
Al igual que en el caso Gaussiano-Gaussiano, en el caso Gaussiano-t también
H ( β)
H ( β)
se pueden obtener condiciones que el VaRα
y CVaRα
deben satisfacer
y a partir de las cuales ser obtenidos. Dichas condiciones se describen y
demuestran en las siguientes Proposiciones.
6
curtosis en exceso de la distribución t no central está dada por Kν = ν−
4 . Despejando el
parámetro ν en términos de Kν se obtiene la relación descrita.
10 Se obtiene despejando el parámetro φ
CE de la ecuación (3.73).
11 Esto se analizará con un poco más de profundidad en la Subsección 3.7.3.
9 La
72
Valor de β* para distintos niveles de concentración
Nivel de Confianza del 95%
Probabilidad de Éstres β
0.04
0.03
0.02
0.01
0
0.9
0.8
1
0.7
0.6
0.5
Rango de Concentración
0.8
0.4
0.6
0.2
0
Valor de δ
Fig. 3.12: β∗ por Simulación. Caso Gaussiano-t.
Número de muestras generadas
Nivel de Confianza del 95%
5
No de muestras generadas
x 10
2
1.5
1
0.5
0
0.9
0.8
0.7
0.6
Rango de Concentración
0.5
0
0.2
0.4
0.6
0.8
1
Valor de δ
Fig. 3.13: Número de muestras generadas para obtener c
β∗ . Caso Gaussiano-t.
73
H ( β)
Proposición 3.14. El VaRα
es solución de la ecuación
u − µCE
u − µN
√
=α
βTν
+ (1 − β ) N
φCE
σN
(3.74)
para u ∈ R.
H ( β)
Demostración. Por definición, si u = VaRα , debe satisfacer


1+ ν
2
Z u
2 −( 2 )
1 x −µ N
(
x
−
µ
)
1
−
β
−
CE
dx = α (3.75)
 βCν 1 +
+ √
e 2 σN
φCE ν
−∞
2πσN
o, de forma equivalente
Z u
β
−∞
Cν 1 +
( x − µCE
φCE ν
−(
)2
1+ ν
2
)
dx + (1 − β)
Z u − 12
e
−∞
√
x −µ N
σN
2
2πσN
dx = α (3.76)
Para simplificar la primera integral de la ecuación anterior, se puede hacer el
√
u−µ
cambio de variable m(u) = √φ CE , y notando que φCE Cν es la constante de
CE
normalización para una distribución t de Student, se tiene que
Z u
−∞
Cν
( x − µCE )2
1+
φCE ν
−( 1+2 ν )
dx =
Z m(u) p
−∞
φCE Cν
= Tν (m(u))
u − µCE
√
= Tν
φCE
m2
1+
ν
−( 1+2 v )
dm
(3.77)
La segunda integral de la ecuación (3.76) es idéntica la ecuación (3.62) de la
demostración de la Proposición 3.12.
H ( β)
Proposición 3.15. El CVaRα
H ( β)
CVaRα
=
√
φCE ν
m ( u )2
1+
f t (m(u)) + µCE Tν (−m(u))
ν−1
ν


2
u−µ
− 21 σ N
N
1 − β  σB e
µN − u 
√
+
+ µN N

 (3.78)
1−α
σN
2π
β
1−α
H ( β)
donde u = VaRα
está dado por
y m(u) =
(u√
−µCE )
.
φCE
H ( β)
Demostración. Dado u = VaRα
H ( β)
, el CVaRα
74
está dado por la expresión
1
1−α
Z ∞
u

2
 βCν x 1 + ( x − µCE )
φCE ν
−( 1+2 ν )
+
1−β
√
2πσN
xe
− 12
x −µ N
σN
2

dx
La integral de la expresión anterior puede ser escrita como
Z ∞
β
u
Cν x 1 +
( x − µCE
φCE ν
−(
)2
1+ ν
2
)
dx + (1 − β)
Haciendo el cambio de variable m(u) =
expresión anterior, se obtiene:
Z ∞
u
( x − µCE )2
Cν x 1 +
φCE ν
u−µCE
√
φCE
Z ∞ − 12
xe
√
u
x −µ N
σN
2
2πσN
dx
(3.79)
en la primera integral de la
−( 1+2 ν )
dx =
Z ∞
m(u)
C(
p
m2
φCE m + µCE ) 1 +
ν
−( 1+2 ν )
dm
(3.80)
√
donde C = Cν φCE es la constante de normalización de una distribución t de
Student. La ecuación (3.80) a su vez es igual a
p
−( 1+2 ν )
−( 1+2 v )
Z ∞
m2
m2
Cm 1 +
dm + µCE
C 1+
dm
ν
ν
m(u)
m(u)
(3.81)
Z ∞
φCE
La primera integral de la expresión (3.81) puede ser simplificada usando el
cambio de variable y(m) = m2 /ν, obteniéndose:
Z ∞
m2
Cm 1 +
ν
m(u)
−( 1+2 ν )
Z ∞
ν
1+ ν
C (1 + y ) − ( 2 )
dy
2
m(u)2 /ν
∞
1+ ν
C (1 + y)−( 2 )+1 =
− 1+2 ν + 1 m(u)2
dm =
ν
∞
ν
−( 1+2 ν ) =
(1 + y ) C (1 + y )
m ( u )2
1−ν
ν
ν
m ( u )2
=−
1+
f t (m(u)), (3.82)
1−ν
ν
por otra parte,
Z ∞
m2
C 1+
ν
m(u)
−( 1+2 v )
dm = 1 − Tν (m(u)) = Tν (−m(u)).
75
(3.83)
Sustituyendo (3.82) y (3.83) en (3.81), se tiene que
√
φCE ν
ν−1
m ( u )2
1+
ν
f t (m(u)) + µCE Tν (−m(u))
(3.84)
es igual a la primera integral en la ecuación (3.79), mientras que la segunda integral de la ecuación (3.79) puede ser obtenida de directamente de la ecuación
(3.70).
Con base en las dos proposiciones anteriores se obtuvo la probabilidad de
estrés óptima β∗ , para los mismos niveles de aversión al riesgo y rangos de
concentración considerados en la Subsección 3.7.1. Los resultados se muestran
en la Figura 3.14.
Valor de β* para distintos niveles de concentración
Nivel de Confianza del 95%
Probabilidad de Éstres β
0.04
0.03
0.02
0.01
0
0.9
0.8
1
0.7
0.6
Rango de Concentración
0.8
0.4
0.6
0.5
0.2
0
Valor de δ
Fig. 3.14: Gráfica de β∗ con respecto a δ, para distintos niveles de concentación
mínima y α = 95%.
Como era de esperarse, los resultados son muy parecidos a los obtenidos
aplicando el algoritmo de simulación. Para verificar esto, se calcularon la
diferencias entre las superficies de β∗ calculada mediante simulación β∗sim y
aquélla obtenida por integración numérica β∗num . Dicha superficie "diferencia"
se muestra en la Figura 3.15.
Como se puede observar a partir de la Figura 3.15, las diferencias en general son positivas, indicando que el método de simulación tiende a subestimar
la probabilidad de estrés óptima. También puede observarse que al igual que
en el caso Gaussiano-Gaussiano las mayores diferencias se dan cuando β∗ es
aproximadamente cero.
76
Diferencias de β* simulada vs β* por integración numérica,
para distintos niveles de concentración.
Nivel de Confianza del 95%
−3
Diferencias en el cálculo de β*
x 10
3
2
1
0
−1
0.9
0.8
0.7
0.6
0.5
Rango de Concentración
0
0.2
0.4
0.6
0.8
1
Valor de δ
Fig. 3.15: Gráfica de las diferencias de β∗sim − β∗num , para distintos valores de δ
y rangos de concentación, con α = 95%. Caso Gaussiano-t.
3.7.3
Comparación entre el modelo Gaussiano-Gaussiano y el
Gaussiano-t
Finalmente, para terminar esta sección, se comparan los resultados obtenidos
con los dos tipos de distribución híbrida considerados. Para ello, se calculó la diferencia entre la superficie de probabilidades de estrés del modelo
Gaussiano-Gaussiano, denotada β∗N , y la superficie correspondiente del modelo Gaussiano-t, denotada β∗T . Ambas superficies fueron calculadas mediante integración numérica. Dicha superficie diferencia se muestra en la
Figura 3.16.
Diferencias β*N − β*T para distintos niveles de concentración
Nivel de Confianza del 95%
Diferencias en el cálculo de β*N−β*T
−4
x 10
10
5
0
−5
0.9
0.8
0.7
0.6
Rango de Concentración
0.5
0
0.2
0.4
0.6
0.8
1
Valor de δ
Fig. 3.16: Diferencia entre β∗N y β∗T .
Como puede apreciarse a partir de la Figura 3.16, la probabilidad de es-
77
trés obtenida mediante una distribución híbrida del tipo Gaussiano-Gaussiano
prácticamente no difiere respecto a la obtenida mediante una distribución
híbrida del tipo Gaussiano-t, ya que las diferencias más grandes son del orden
de 10−4 .
También puede observarse a partir de la Figura 3.16, que las diferencias
son en general positivas, o equivalentemente, que la probabilidad de estrés en
el caso Gaussiano-Gaussiano es mayor a la probabilidad de estrés en el caso
Gaussiano-t. Esto se debe a que la distribución t no central modela mejor
las colas pesadas de la distribución empírica y por ende se requiere de una
ponderación menor de la distribución en condiciones de estrés para obtener
un buen ajuste.
3.8
Comparación de β∗ con el factor de ajuste F ∗
Tanto en este capítulo como en el anterior, el objetivo central ha sido el mismo:
desarrollar una metodología para medir el riesgo de mercado -en términos
del VaR y CVaR- de manera más precisa bajo condiciones de distorsión de
los precios. Para ello, en ambos casos se ha partido del mismo supuesto
estándar consistente en que los rendimientos se comportan de acuerdo a una
distribución Gaussiana. La diferencia entre ambas metodologías estriba en la
forma en que se parte, o se adecua dicho supuesto. En un caso se optó por
ajustar el parámetro de desviación estándar mediante un cierto factor de ajuste
F ∗ . En el otro caso se decidió construir una distribución, que fuera por un
lado consistente con la distribución Gaussiana bajo condiciones normales y,
por el otro, que considerará la probabilidad de condiciones de estrés, medida
en términos de una probabilidad β∗ , en que las pérdidas se distribuyen de
acuerdo a otra distribución no necesariamente Gaussiana y no necesariamente
con los mismos parámetros. Dado que tanto el factor de ajuste F ∗ como la
probabilidad de estrés β∗ son determinadas esencialmente por el mismo tipo
de criterio, se puede afirmar que son equivalentes y por lo tanto, es de interés
estudiar esta equivalencia. Para tal efecto, se decidió usar el nivel de aversión
al riesgo δ como variable de "triangulación" o de "vinculación", suponiendo
un nivel de concentración c y un nivel de confianza α fijos. Es decir, dados c
y α se conocen F ∗ (δ) y β∗ (δ) para cada δ ∈ [0, 1], de donde F ∗ se asocia a
β∗ si y sólo si F ∗ y β∗ corresponden a la misma δ. De esta manera, para el
caso concreto del Bono M Diciembre 2007, se construyeron las gráficas de las
Figuras 3.17 y 3.18, que corresponden, respectivamente, a los casos GaussianoGaussiano y Gaussiano-t.
Como se observa claramente en dichas gráficas, la probabilidad de estrés
β∗ se incrementa conforme el factor de ajuste F ∗ así lo hace también. Este
comportamiento es consecuencia del comportamiento monotónico de F ∗ y β∗
con respecto a δ anteriormente observado.
Desde un punto de vista práctico, la relación derivada entre F ∗ y β∗ es útil
78
Relación entre F* y β*
0.04
0.035
Valor de β*
0.03
0.025
50%
60%
70%
80%
0.02
0.015
0.01
0.005
0
0.8
0.9
1
1.1
1.2
1.3
1.4
1.5
Valor de F*
Fig. 3.17: Relación entre F ∗ y β∗ para distintos rangos de concentración y
α = 95%. Caso Gaussiano-Gaussiano.
Relación entre F* y β*
0.04
0.035
Valor de β*
0.03
0.025
50%
60%
70%
80%
0.02
0.015
0.01
0.005
0
0.8
0.9
1
1.1
1.2
1.3
1.4
1.5
Valor de F*
Fig. 3.18: Relación entre F ∗ y β∗ para distintos rangos de concentración y
α = 95%. Caso Gaussiano-t.
79
ya que, por ejemplo, permite al administrador de riesgos determinar el factor
de ajuste a aplicar a la desviación estándar estimada dada una evaluación,
posiblemente subjetiva, de la probabilidad de estrés o crisis implícita asociada
a dicho factor.
80
3.9
Conclusiones
La motivación central de este capítulo fue desarrollar una metodología para
medir el riesgo de mercado en condiciones de distorsión de los precios la cual,
a diferencia de lo que se hizo en el Capítulo 2, incorpora la posibilidad de un
evento de estrés en el que la distribución de probabilidad de las pérdidas es
distinta a la distribución Gaussiana típicamente considerada en condiciones
normales.
De esta forma, se desarrolló una metodología para la construcción de
una distribución de probabilidad "híbrida", que considera simultáneamente
el comportamiento de los rendimientos tanto en condiciones normales como
en condiciones de estrés, a partir de la cual se mide el riesgo de mercado en
términos del VaR y CVaR. Para determinar dicha distribución híbrida, se requiere predeterminar un par de distribuciones, una que caracteriza los rendimientos en condiciones normales y otra que lo hace en condiciones de estrés,
las cuales se combinan probabilísticamente, en términos de una probabilidad
de estrés, de tal forma que las mediciones de riesgo obtenidas con base en
dicha distribución híbrida se ajusten "lo mejor posible" a las correspondientes medidas de riesgo observadas. Específicamente, bajo el criterio de que
la desviación cuadrática de los valores estimados y observados sea mínima.
Por lo tanto, la determinación de la distribución híbrida se formula matemáticamente como la solución de un problema de optimización, muy similar al
planteado en el capítulo anterior para determinar el factor de ajuste. Dicha
formulación presenta las siguientes ventajas:
• La formulación permite asignar el peso relativo que tiene la desviación
cuadrática relacionada con el CVaR respecto a aquélla vinculada con el
VaR. El valor de dicho peso relativo, denominado δ, se puede asociar,
al menos intuitivamente, a un cierto nivel de aversión al riesgo en el sentido de que entre mayor sea el valor de este ponderador, mayor es la
importancia se le da al valor estimado del CVaR, la medida de riesgo
más conservadora de las dos consideradas en el presente análisis.
• El problema de optimización tiene solución para cualquier par de distribuciones que conforman la distribución híbrida, bajo el supuesto de
que dichas distribuciones satisfagan una cierta condición de dominancia
estocástica. Dicho supuesto es típicamente satisfecho en la práctica.
Por otro lado, dado que desafortunadamente el problema de optimización no tiene una solución explícita, se propuso y desarrolló una metodología, basada en simulación, para resolver el problema de manera
numérica. Esta metodología presenta las siguientes ventajas:
– No se necesitan conocer fórmulas explícitas (o implícitas) para el
cálculo del VaR y CVaR de la distribución híbrida considerada.
81
– El método se puede aplicar fácilmente para cualquier tipo de distribuciones en condiciones normales y en condiciones de estrés consideradas.
– Es posible, en principio, acotar arbitrariamente el error en la estimación de la probabilidad de estrés con un cierto nivel de confianza
predeterminado.
La metodología desarrollada se aplicó en el contexto particular del Bono M
Diciembre 2007 para dos casos concretos: uno en el que se supone que tanto
la distribución en condiciones normales como la de estrés son Gaussianas, y
otra en el que la distribución en condiciones normales es Gaussiana, pero t no
central en condiciones de estrés. Los resultados obtenidos en cada caso son
los siguientes:
• Gaussiano-Gaussiano:
– El rango de probabilidades es [0.00344%, 3.78408%], para α=95%.
– Para cualquier nivel de concentración la probabilidad de estrés se
incrementa conforme el parámetro de aversión al riesgo δ se incrementa.
– No hay un efecto claramente discernible de la concentración sobre
la probabilidad de estrés, sin embargo, hay una ligera tendencia de
está a incrementarse conforme aumenta la concentración.
• Gaussiano-t:
– El rango de probabilidades es [0.00346%, 3.81709%], para α=95%.
– Para cualquier nivel de concentración la probabilidad de estrés se
incrementa conforme el parámetro de aversión al riesgo δ se incrementa.
– No hay un efecto claramente discernible de la concentración sobre
la probabilidad de estrés, sin embargo, hay una ligera tendencia de
está a incrementarse conforme aumenta la concentración.
La metodología desarrollada en este capítulo se puede adaptar fácilmente
para
• Incoporar distintos tipos de distribuciones híbridas de riesgo.
• Considerar otro tipo de medidas de riesgo, diferentes al VaR y CVaR.
• Utilizar otras variables de referencia.
82
Conclusiones Generales
El objetivo primario de este trabajo de tesis fue proponer una metodología
para medir el riesgo de mercado en condiciones propicias para la distorsión
de los precios. Así, se determinaron dos metodologías para tal efecto. Ambas
desarrolladas bajo la premisa de adecuar la metodología estándar, que supone
que la distribución de pérdidas se distribuye de acuerdo a una variable aleatoria normal, y considerando como medidas de riesgo el VaR y el CVaR. Una de
estas metodologías determina un Factor de Ajuste que escala el parámetro de
desviación estándar, mientras que la otra construye una Distribución Híbrida
que considera simultáneamente una distribución Gausssiana, para modelar
las pérdidas en condiciones normales, y otra distribución, no necesariamente
Gaussiana, para modelar las pérdidas en condiciones de estrés. En ambos
casos, se busca estimar el riesgo de la manera "más precisa posible". Es decir,
se determinan el Factor de Ajuste y la Distribución Híbrida tales que el riesgo
estimado a partir de ellos sea lo más parecido posible al riesgo observado.
Aunque las metodologías aquí desarrolladas fueron en principio desarrolladas para medir el riesgo de mercado en condiciones propicias para la distorsión de los precios, éstas pueden aplicarse para adecuar la metodología
estándar por cualquier característica o conjunto de características de la distribución de pérdidas que se aleje de los supuestos de dicha metodología. Por
lo tanto, su aplicabilidad es potencialmente bastante amplia.
Tanto la metodología de Factores de Ajuste como la de Distribuciones
Híbridas son formuladas en términos de modelos matemáticos, similares en
espíritu, a partir de los cuales se demuestran varias propiedades teóricas interesantes y los cuales pueden incorporar fácilmente restricciones adicionales,
a fin de adaptarlas a contextos más específicos, así como considerar medidas
de riesgo adicionales o distintas al VaR o CVaR.
Entre las propiedades teóricas demostradas en este trabajo que, en nuestro juicio, sobresale del resto es aquélla relacionada con el comportamiento
monótono creciente del Factor de Ajuste respecto al parámetro de aversión al
riesgo δ . Dicha propiedad, además de ser intuitivamente correcta, se cumple
esencialmente bajo la condición de que la distancia relativa entre el VaR y el
CVaR de la distribución de pérdidas sea "suficientemente grande". A saber,
mayor o igual que la correspondiente distancia en el caso que la distribu83
ción de pérdidas sea una Gaussiana. Esta condición es interesante ya que
induce una partición de las distribuciones de pérdidas: aquéllas que cumplen
la condición, las cuáles denominamos riesgosas, y aquéllas otras que no la
cumplen, llamadas no riesgosas. Creemos que sería de interés ahondar en las
consecuencias de dicha condición.
84
Apéndice A
Convexidad y Condiciones de
Optimalidad
Definición A.1 (Conjunto Convexo). Un subconjunto C de Rn es convexo si y
sólo si
(1 − λ) x + λy ∈ C
∀ x, y ∈ C y λ ∈ (0, 1).
Definición A.2 (Función Convexa). Sea C un conjunto convexo en Rn , entonces f : C → R es una función convexa si y sólo si
f ((1 − λ) x + λy) ≤ (1 − λ) f ( x ) + λ f (y)
∀ x, y ∈ C y λ ∈ (0, 1).
Definición A.3 (Función Cóncava). Sea C un conjunto convexo en Rn . Una
función f : C → R con C convexo, es cóncava si y sólo − f es convexa.
Proposición A.1. Sea f : ( a, b) → R una función dos veces diferenciable y cuya
segunda derivada es continua. Entonces f es convexa (cóncava) en ( a, b) si y sólo si
su segunda derivada f 00 es no negativa (no positiva) en ( a, b).
Demostración. Ver, por ejemplo, Teorema 4.4 de Rockafellar (1970).
Definición A.4 (Condiciones de Optimalidad de Primer Orden). Sea
f : D ⊂ Rn → R. Entonces, se dice que x ∗ ∈ D satisface las condiciones
de optimalidad de primer orden si y sólo si
∇ f ( x ∗ ) = 0.
Teorema A.1. Sea C un conjunto convexo abierto en Rn y f : C → R una función
convexa y diferenciable en C. Entonces x ∗ ∈ C es un mínimo global si y sólo si x ∗
satisface las condiciones de optimalidad de primer orden.
85
Demostración. Es consecuencia directa de la Proposición 2.6 de Zangwill (1969).
86
Apéndice B
Simulación
B.1
Método Monte Carlo
El método Monte Carlo consiste, en su forma más sencilla, en formular algún
juego de azar o proceso estocástico cuyo valor esperado sea la solución al
problema planteado (Bauer, 1958). Sin embargo, puede ser utilizado para
obtener prácticamente cualquier estadística de una distribución por medio de
un muestreo repetido aún si no se conoce su forma parámetrica. Para ilustrar
el método considerése el siguiente ejemplo.
Ejemplo B.1 (Simulación de π). Supóngase que se desea estimar el valor π
con un cierto nivel de precisión. Para ello se formula el siguiente problema
probabilístico: se escogen puntos al azar uniformemente distribuidos sobre
un cuadrado cuyo lado tiene longitud uno, y se cuentan el número de puntos
que se encuentran dentro del cuarto de circunferencia inscrita en el cuadrado,
como se muestra en la Figura B.1.
Así la probabilidad de que un punto se encuentre dentro del área delimitada será exactamente π/4. Más formalmente, sean X y Y variables aleatorias
con distribución uniforme en el intervalo [0, 1], y Sn una variable aleatoria
que cuente el número de ocasiones, en n intentos, en los que X 2 + Y 2 ≤ 1.
nπ
π
Entonces Sn ∼ Binomial( nπ
4 , 4 (1 − 4 )) y E [ Sn /n ] = π/4. Para ver que tan
buena es la aproximación obtenida por medio de la simulación, se calculará la
probabilidad de que el error relativo sea menor o igual a una cierta constante
87
1
Puntos fuera
de la
circunferencia
0.9
0.8
0.7
Y
0.6
0.5
Puntos dentro
de la
circunferencia
0.4
0.3
0.2
0.1
0
0
0.2
0.4
0.6
0.8
1
X
Fig. B.1: Simulación de π.
e > 0. Así:
Sn /n − π/4 Sn − n(π/4) P ≤ e = P n(π/4) ≤ e
π/4
s
"
#
Sn − n(π/4)
n(π/4)
= P p
≤e
n(π/4)(1 − π/4) (1 − π/4)
s
s
!
!
n(π/4)
n(π/4)
≈N e
− N −e
(1 − π/4)
(1 − π/4)
s
!
n(π/4)
− 1.
= 2N e
(1 − π/4)
A partir de esto es posible definir la función
s
!
n(π/4)
− 1,
Ψ(e, n) = 2N e
(1 − π/4)
(B.1)
que indica la probabilidad de tener un error relativo menor o igual a e en n
simulaciones1 . Resolviendo la ecuación Ψ(e, n) = 0.95 para distintos valores
de e, se puede determinar el número de simulaciones necesarias para alcanzar
la precisión requerida en la estimación, con un nivel de confianza del 95%. Los
resultados se muestran en la Tabla B.1. Como puede observarse a partir de
dicha tabla, el número de simulaciones necesarias crece rápidamente respecto
a la reducción en el error de la aproximación, siendo necesario aumentar el
número de simulaciones por un factor de 100 para reducir el error en un factor
de 10.
1 Observesé
que se ha utilizado el teorema del límite central para aproximar el verdadero valor.
88
Tab. B.1: Simulación de π
B.2
Error Relativo
Número de Simulaciones
10−1
10−2
10−3
10−4
10−5
10−6
1.04964 × 102
1.04964 × 104
1.04964 × 106
1.04964 × 108
1.04964 × 1010
1.04964 × 1012
Simulación de Distribuciones Híbridas
Sea X una v.a. cuya función de distribución es
FH ( x ) = βFA ( x ) + (1 − β) FB ( x ),
(B.2)
donde FA y FB son funciones de distribución y β ∈ [0, 1]. Este tipo de distribuciones se denominan distribuciones híbridas y se definen formalmente
en la Sección 3.2. Para generar una v.a. con dicha distribución se puede usar
el siguiente algoritmo:
1. Se genera un valor aleatorio de una distribución uniforme [0,1], digamos
U.
2. Si U < β entonces se genera un valor aleatorio a partir de la distribución FA . En caso contrario, se genera un valor aleatorio a partir de la
distribución FB .
El procedimiento anterior se repite un número predeterminado de veces, digamos n, a fin de obtener una muestra de tamaño n de la v.a. X.
89
Apéndice C
El caso del sesgo en la
estimación de β∗
Koji & Maasaki (2005) analizan el problema del sesgo porcentual en los estimadores tradicionales del VaR y CVaR. El sesgo porcentual del VaR es definido
por:
λvm =
Media del VaR − VaR∗
VaR∗
(C.1)
donde VaR∗ denota el valor teórico del VaR. Asimismo el sesgo porcentual del
CVaR es definido por:
λcv
m =
Media del CVaR − CVaR∗
CVaR∗
(C.2)
donde CVaR∗ denota el CVaR teórico. El procedimiento utilizado por Koji
& Maasaki (2005) consiste en obtener por simulación N muestras aleatorias
indepedientes, de tamaño m cada una, y a partir de cada muestra, estimar el
VaR y CVaR promedios, los cuales se comparan contra su valor teórico para
obtener el sesgo porcentual como definido por (C.1) y (C.2). Koji & Maasaki
(2005) analizan el caso particular de la distribución t con 3, 4 y 5 grados
de libertad, tomando N = 1000 y m = 100, 200 y 300 y concluyen que para
m = 300, λvm varía entre -2.97% y -4.18% mientras que λcv
m varía entre -0.79%
y 1.1%.
H ( β)
dα
Ya que la estimación de c
β∗i depende de los estimadores VaR
H ( β)
H ( β)
\α
y CVaR
H ( β)
del VaRα
y CVaRα , respectivamente, es de esperarse que exista un sesgo
en su estimación. Luego entonces se tendrá que
∗
β
E[ c
β ∗ ] = (1 + λ m ) β ∗
90
(C.3)
β∗
donde λm denota el sesgo porcentual en la estimación de β∗ y esta definido
como:
β∗
λm =
E[ c
β∗ ] − β∗
β∗
(C.4)
Asimismo Koji & Maasaki (2005) muestran evidencia de que el sesgo en
la estimación del VaR y CVaR se reducen conforme se incrementa el tamaño
de la muestra, o en otras palabras, que los estimadores son asintóticamente
β∗
insesgados, por lo que es plausible suponer que λm sea asintóticamente insesgado. Por lo tanto, es de esperarse que para un valor de m "suficientemente
grande", el sesgo en la estimación de β∗ sea "pequeño".
91
Bibliografía
Acerbi, C., Nordio, C., & Sirtori, C. (2001). Expected Shortfall as a Tool for
Financial Risk Management. ArXiv Condensed Matter e-prints.
Andreev, A. & Kanto, A. (2005). Conditional Value-at-Risk estimation using
non-integer values of degrees of freedom in Students t-distribution. The
Journal of Risk, 7(2).
Artzner, P., Delbaen, F., Eber, J. M., & Heath, D. (1999). Coherent measures of
risk. Mathematical Finance, 9(3), 203–228.
Bauer, W. F. (1958). The Monte Carlo Method. Journal of the Society for Industrial
and Applied Mathematics, 6(4).
Casella, G. & Berger, R. L. (1990). Statistical Inference. Duxbury Press.
Embrechts, P., Klüppelberg, C., & Mikosch, T. (1997). Modelling Extremal Events
for Insurance and Finance. Berlin: Springer.
Koji, I. & Maasaki, K. (2005). On the significance of expected shortfall as a
coherent risk measure. Journal of Banking and Finance.
McNeil, A. J. (1999). Internal Modelling and CAD II, chapter Extreme Value
Theory for risk managers, (pp. 93–113). RISK Books.
Nelson, C. R. & Siegel, A. F. (1987). Parismonious modeling of yield curves.
The Journal of Business, 60(4).
Rockafellar, T. R. (1970). Convex Analysis. Princeton University Press.
Rockafellar, T. R. & Uryasev, S. P. (2002). Conditional Value-at-Risk for General
Loss Distributions. Journal of Banking and Finance.
Sarma, M. (2005). Characterization of the tail behavior of financial returns:
studies from India. Working Paper, EURANDOM.
Spivak, M. (1996). CALCULUS, Second Edition. W.A. Benjamin, Inc., New York.
92
Svensson, L. (1994). Estimating and Interpreting Forward Interest Rates: Sweden. Working Paper No. 4871, NBER. National Bureau of Economic Research.
Zangwill, W. (1969). Nonlinear Programming: A Unified Approach. Prentice-Hall.
93