Resolver los siguientes sistemas:

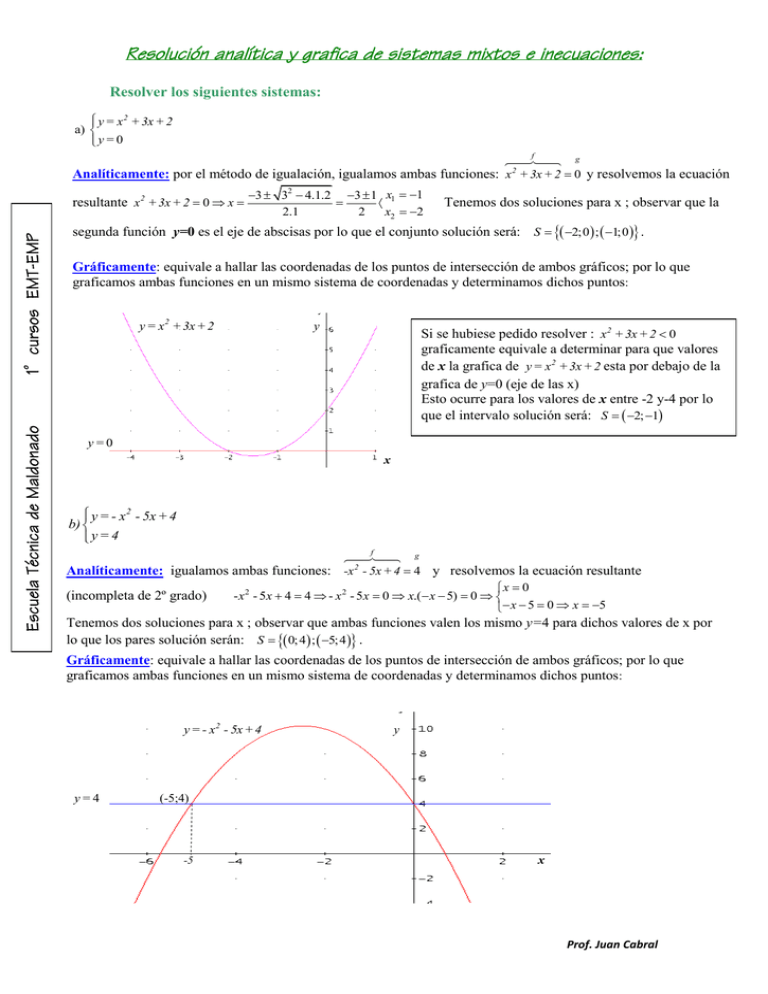
Resolución analítica y grafica de sistemas mixtos e inecuaciones:
Resolver los siguientes sistemas:
2

 y = x + 3x + 2
a) 

y= 0
f
g
Analíticamente: por el método de igualación, igualamos ambas funciones: x + 3x + 2  0 y resolvemos la ecuación
2
Escuela Técnica de Maldonado
1° cursos EMT-EMP
resultante x 2 + 3x + 2  0  x 
3  32  4.1.2 3  1 x1  1


2.1
2
x2  2
Tenemos dos soluciones para x ; observar que la
segunda función y=0 es el eje de abscisas por lo que el conjunto solución será: S   2;0  ;  1;0  .
Gráficamente: equivale a hallar las coordenadas de los puntos de intersección de ambos gráficos; por lo que
graficamos ambas funciones en un mismo sistema de coordenadas y determinamos dichos puntos:
y = x2 + 3x + 2
y
Si se hubiese pedido resolver : x2 + 3x + 2  0
graficamente equivale a determinar para que valores
de x la grafica de y = x2 + 3x + 2 esta por debajo de la
grafica de y=0 (eje de las x)
Esto ocurre para los valores de x entre -2 y-4 por lo
que el intervalo solución será: S   2; 1
y=0
x
2

 y = - x - 5x + 4
b) 

y= 4
f
g
Analíticamente: igualamos ambas funciones: -x - 5x + 4  4 y resolvemos la ecuación resultante
2
(incompleta de 2º grado)
x  0
- x 2 - 5 x  4  4  - x 2 - 5 x  0  x.(  x  5)  0  
 x  5  0  x  5
Tenemos dos soluciones para x ; observar que ambas funciones valen los mismo y=4 para dichos valores de x por
lo que los pares solución serán: S   0;4  ;  5;4  .
Gráficamente: equivale a hallar las coordenadas de los puntos de intersección de ambos gráficos; por lo que
graficamos ambas funciones en un mismo sistema de coordenadas y determinamos dichos puntos:
y = - x 2 - 5x + 4
y= 4
y
(-5;4)
-5
x
Prof. Juan Cabral
Resolución analítica y grafica de sistemas mixtos e inecuaciones:

c) Dadas las funciones: f :
1) Resolver en
2
/ f ( x) = x2 - 4x + 1 g :

/ g ( x) = 3x - 11
2

 y = x - 4x + 1


 y = 3x - 11
el sistema:
f
g
Analíticamente: igualamos ambas funciones: x - 4x + 1  3x  11 y resolvemos la ecuación resultante
2
x 2 - 4x + 1  3x - 11  x 2 - 7 x + 12  0  x 
7  (7)2  4.1.12 7  1 x1  4


2.1
2 x2  3
Tenemos dos soluciones para x ; para hallar los valores de y sustituimos dichos valores en una de las funciones;
por ejemplo en g(x) para x=3 nos queda: y  3.(3) -11  2 y para x=4 nos queda: y  3.(4) -11  1
1° cursos EMT-EMP
por lo que los pares solución serán: S   3; 2  ;  4;1 .
Gráficamente: Equivale a hallar las coordenadas de los puntos de intersección de ambos gráficos; por lo que
graficamos ambas funciones en un mismo sistema de coordenadas y determinamos dichos puntos:
g
y = x2 - 4x + 1
Escuela Técnica de Maldonado
(4;1)
-5
f
(3;-2)
y = 3x  11
2) Resolver en : f ( x)  g ( x)
Gráficamente:
Equivale a determinar para que valores de x la grafica de f ( x) esta por encima de la grafica de g ( x) .
Por lo que el intervalo solución será: S   ,3  (4, ) .
Analíticamente:
f
g
Es resolver la inecuación: x - 4x + 1  3x - 11  x 2 - 7 x + 12  0 Equivale a preguntar: ¿para que valores de x la
expresión es positiva?; para contestar esto debemos estudiar el signo, previamente, hallando los ceros.
2
 x1  4
 x2  3
i) Ceros: x 2 - 7 x + 12  0  
(hallados en 1))
sig x2 - 7 x + 12
++++ 0-------- 0 ++++
3
4
iii) Intervalo solución: S   ,3  (4, )
ii) Signo:
Prof. Juan Cabral