UNIVERSIDAD DE LA FRONTERA

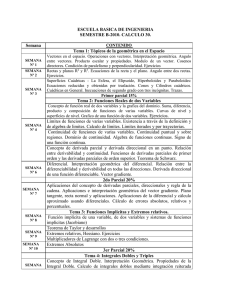
UNIVERSIDAD DE LA FRONTERA
TEMUCO CHILE
PROGRAMA DE ASIGNATURA
UNIVERSIDAD DE LA FRONTERA
I.- IDENTIFICACIÓN DE LA ASIGNATURA
Asignatura
: CALCULO III
Carrera
Código
Horas
Calidad
Tipo de formación
Carácter
Ponderación
Régimen
Curso
Semestre que se imparte
Año académico
Prerrequisitos
Departamento
Facultad
:
:
:
:
:
:
:
:
:
:
:
:
:
:
ICII (3002)-ICIB(3080)-ICE(3012)-IM(3084)
IME 208
4 ( 4 0 4)
Obligatoria
Básica
Teórico
Teórico 100%, Práctico 0%
Semestral
Año 2, Nivel 3
Primero y Segundo
2005
CALCULO II
Matemática y Estadística
Ingeniería, Ciencias y Administración
II.- DESCRIPCIÓN DE LA ASIGNATURA
Asignatura anual dirigida a los alumnos de las carreras de Ingenierías
Civiles e Ingeniería Matemática de calidad obligatoria y carácter teórico de
tercer nivel orientado a proporcionar herramientas básicas del estudio de
funciones en varias variables necesarias para el estudio de tópicos en
ingeniería. Contempla lo referente al cálculo diferencial e integral de
funciones vectoriales.
III.-
OBJETIVOS GENERALES Y ESPECIFICOS (cognitivos,
procedimientos y actitudinales).
a)
Objetivos Generales.-
En este curso los alumnos y alumnas:
1)
Adquirirán los conceptos básicos del cálculo
diferencial e integral de funciones vectoriales.
2)
Aplicarán las técnicas básicas del cálculo diferencial
e integral de las funciones vectoriales en la
resolución de problemas de ciencias e ingeniería.
3)
Adquirirán la base conceptual y operatoria para
enfrentar con éxito los estudios de especialidad en
ingeniería.
b)
Objetivos Específicos.1)
Cognitivos:
Al finalizar el curso los alumnos y alumnas deberán:
1)
2)
3)
2)
Desarrollar su capacidad de razonamiento lógico, de
abstracción y de generalización, que forme y
enriquezca su saber matemático.
Adquirir habilidades básicas que le permitan plantear
y resolver situaciones problemáticas.
Desarrollar su capacidad analítica para el estudio de
situaciones problemáticas referente al cálculo
matemático.
Procedimentales:
Al finalizar el curso los alumnos deberán:
1)
2)
3)
4)
5)
6)
Determinar la continuidad y diferenciabilidad en un
punto y en una región de una función de varias
variables.
Calcular la derivada direccional y parcial de una
función de varias variables.
Calcular máximos y mínimos de una función de
varias variables.
Calcular integrales múltiples.
Resolver problemas aplicando integrales múltiples.
Aplicar los teoremas de Green, Gauss y Stockes en
el cálculo de integrales de línea y superficie.
3)
Actitudinales.Al finalizar el curso los alumnos deberán:
1)
2)
IV.-
Percibir la matemática como una disciplina que ha
evolucionado y que continua desarrollándose, y que
responde en algunas ocasiones a la necesidad de
resolver problemas prácticos, pero que también se
plantean problemas propios que a menudo son por
el solo placer intelectual y estético.
Valorar el desempeño grupal y la distribución de
tareas para conseguir los objetivos de: seguridad y
confianza en si mismo, inventiva y creatividad,
capacidad de liderazgo, responsabilidad, tolerancia,
autoestima, hábitos y valores de trabajo y estudio.
CONTENIDOS.UNIDAD 1.-. CALCULO DIFERENCIAL EN R^N.
1)
2)
3)
4)
5)
6)
7)
8)
9)
Topología de R^n. Definición de la norma, normas
equivalentes. Vecindad, punto de acumulación.
Límite y continuidad: Teoremas de funciones continuas.
Derivadas direccionales. Derivadas parciales.
Gradiente y matriz Jacobiana.
Regla de la cadena y Teorema del Valor Medio.
Teorema de Taylor
Teorema de la Función Implícita.
Estudio de valores extremos sin restricciones.
Multiplicadores de Lagrange.
UNIDAD 2.- CÁLCULO INTEGRAL EN R^N.
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
Partición, intervalos. Integral de Rieman.
Integración sobre conjuntos acotados de R^n
Existencia de funciones integrables. Teorema de cambio de
variables.
Cálculo de integrales dobles y triples.
Aplicaciones de integrales dobles y triples al cálculo de
áreas, volúmenes, centros de masa y momentos.
Integrales de línea. Integración de campos gradientes.
Teoremas fundamentales para integral de línea.
Aplicaciones de la integral de línea de campos escalares y
vectoriales.
Divergencia y rotacional.
Integral de superficie. Integral de campo escalar y vectorial.
Aplicaciones.
Teoremas de Green, Gauss y Stokes.
Aplicaciones al estudio de campos eléctricos y
magenéticos.
V.-
RECURSOS METODOLÓGICOS.Trabajos grupales e individuales de talleres. Trabajos de
Laboratorio de Computación. Presentación y evaluación de
proyectos.
VI.-
EVALUACIÓN.Según régimen vigente.
VII.- BIBLIOGRAFIA.
BASICA.1)
2)
3)
4)
Stewart,
James.
“CALCULO
DIFERENCIAL
E
INTEGRAL”. México. Thomson Editores. 2001, 680 pág.
Larson R. Hostetter. “CALCULO DIFERENCIAL E
INTEGRAL” (Volumen 2 ). México, McGraw Hill. 1998. 700
pág.
Valenzuela, Pedro H. “ MATEMATICA “ Volumen 4 “.
Temuco. Editorial Páginas. 2003, 250 pág.
Marden y Tromba “ CALCULO VECTORIAL “. Addison
Wesley Iberoamericana. 2000, 450 pág.
COMPLEMENTARIA.1)
2)
3)
4)
5)
Purcell-Varberg-Rigdon. “ CALCULO “ Pearson Education,
2001, 800 pág.
Bradley-.Smith “ CALCULO DE VARIAS VARIABLES “
Prentice Hall. 1998., 460 págAbellanas-Galindo. “MÉTODOS DE CÁLCULO”. McGrawHill. 1990. 450 pág.
Pita Ruiz, Claudio “ CALCULO VECTORIAL “ Pretice Hall,
2000, 800 pág.
O’Neil, Meter. “ MATEMATICAS AVANZADAS PARA
INGENIERIA” Continental S.A. 1999, 780 pág.