Ejercicios sobre notación científica y cambio de unidades

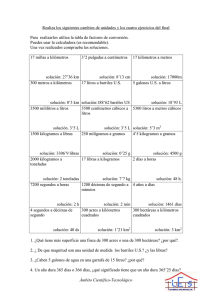
REPASO DE CAMBIOS DE UNIDADES DEL AÑO PASADO
Antes de los ejercicios puedes encontrar pequeñas explicaciones teóricas.
Van con sus soluciones para que compruebes si sabes hacerlos.
CONCEPTOS GENERALES I:
Te recomiendo que visites http://platea.pntic.mec.es/pmarti1/inicio.htm
Pincha en la pestaña de 3º de la E.S.O. Hay más ejercicios para practicar y te explican
como se realizan.
Conceptos generales I: la notación científica y el cambio de unidades.
Notación científica
¿Qué significan los símbolos en la notación decimal?
Para no escribir números muy grandes ni muy pequeños (o números que simplemente
no nos gusten porque nos parezcan feos) se usan una serie de símbolos, ejemplos de ello
serían, 7’5 kg (kilogramos) en lugar de 7500 g (gramos), 3’3 cm (centímetros) en lugar
de 0’033 m (metros), 550 ml (mililitros) en lugar de 0’55 l (litros)…
Símbolo
T
G
M
k
h
da / D
d
Nombre (prefijo)
Tera
Giga
Mega
Kilo
Hecto
Deca
Unidad
Deci
10n
12
10
109
106
103
102
101
100 = 1
10-1
c
Centi
10-2
m
Mili
10-3
µ
Micro
10-6
n
Nano
10-9
p
Pico
10-12
Equivalencia
1000000000000 unidades = 1 T unidad
1000000000 unidades = 1 G unidad
1000000 unidades = 1 M unidad
1000 unidades = 1 k unidad
100 unidades = 1 h unidad
10 unidades = 1 da unidad
Ninguna
0’1 unidades = 1 d unidad
o también
1 unidad = 10 d unidades
0’01 unidad = 1 c unidad
o también
1 unidad = 100 c unidades
0’001 unidad = 1 m unidad
o también
1 unidad = 1000 m unidades
0’000001 unidades = 1 µ unidad
o
1 unidad = 1000000 µ unidad
0’000000001 unidades = 1 n unidad o
1 unidad = 1000000000 n unidad
0’000000000001 unidades = 1 p unidad o
1 unidad = 1000000000000 p unidades
Nota: Unidades son m (metro), l (litro), ºC (grado centígrado), g (gramo)…
¿Qué entendemos por número en notación científica?
Es el número expresado como multiplicación de un número, que solo tiene una cifra en
la parte entera y esa cifra es distinta de cero, por una potencia de base 10.
Recuerda que 102 = 100, 105 =100000, 10-3 = 0’001, 10-1 = 0’1…
Ejemplos: 567 = 5’67·102 , 0’0034 = 3’4·10-3…
1) Expresa en notación científica los siguientes números:
0'00004567
98257'9845
23'57
90'00034
4537'987654
0'0056
0'09
23'765
0'4539
200000000
230000
0'00000005
2) Expresa los siguientes números eliminando la base diez:
Ámbito Científico-Tecnológico
a. 6·10-3
b. 9'45·107
c. 34323·102
d. 0'004·10-4
-5
3
-2
e. 685'86·10
f. 0'005·10
g. 0'00005·10
h. 9843592·10-5
3) De los números del ejercicio anterior, ¿cuáles podrían considerarse bien escritos
en notación científica?
4) Sustituye los valores de los símbolos que acompañan a la unidad por su valor:
4 mm
5'05 kl
34 Me.V
4'0089 nJ
34 µN
5) Usando los prefijos (sus símbolos) de las potencias de base 10 más famosas,
indica las siguientes magnitudes “de la forma más cómoda y con los menos
ceros posibles” (aunque no cumplan con la notación científica).
Ejemplos:
56000 m
35000000 e.V = 35 Me.V
0’0003 g
0’0000073 l = 7’3 µl
65900 N
0’04 J
Soluciones:
1) Soluciones: 4'567·10-5, 9'82579845·104, 2'357·101, 9'000034·101, 4'537987654·103, 5'6·10-3, 9·10-2, 2'3765·101,
4'539·10-1, 2·108, 2'3·105, 5·10-8.
2) Soluciones: 0'006, 94500000, 3432300, 0'0000004, 0'0068586, 5, 0'0000005, 98'43592
3) Soluciones: el a y el b.
4) Soluciones: 4·10-3 m, 5'05·103·l, 34·106 e.V, 4'0089·10-9 J, 34·10-6 N
5) Soluciones (nota, puede haber otras soluciones igualmente adecuadas): 56 km, 0’3 mg, 4 cJ, 65’9 kN (659 hN).
Cambios de unidades:
Todas las unidades de una misma magnitud están relacionadas de alguna forma, por ello
se pueden realizar cambios de unidades entre unas y otras. Lo normal (en el caso de la
temperatura no es así) es una proporcionalidad (una relación de igualdad).
Esa relación de igualdad se puede transformar en un factor de conversión. El factor de
conversión es la expresión (la fracción) por la que tendremos que multiplicar la unidad
original para transformarla en la unidad deseada.
Ejemplo: Magnitud dinero, dos unidades posibles podrían ser los dólares y los euros.
Supongamos que nos dicen que 1 euro son 1’53 dólares. La relación de igualdad será 1
€ = 1’53 Dólares. El factor de conversión será, según queramos pasar Dólares a Euros
1€
1'53
Dólares
o Euros a Dólares,.
o
respectivamente.
1'53
Dólares 1€
¿Cómo se realiza un cambio de unidades poco complejo?
Primero se identifica cuantas unidades se quieren cambiar. Después se buscan las
relaciones de igualdad entre ellas. Seguidamente se selecciona de que forma
utilizaremos el factor de conversión (si la unidad que queremos cambiar esta en el
numerador de la expresión original deberá estar en el denominador del factor de
conversión, también funciona al revés). Lo último es hacer el cambio de unidades.
Ejemplo: 3 dólares a euros. 3 dólares·(1€/1’53dólares)=1’96 €
¿Cómo se realiza un cambio de unidades más complejo?
Un caso complejo sería que no tuviéramos un solo factor de conversión, pero que si
tuviéramos varios factores de conversión, entonces usaremos tantas igualdades como
necesitemos, una detrás de otra.
Ejemplo: 2 dl→mm3 igualdades que tenemos 1l=10dl, 1000cm3=1l y 1000mm3=1cm3
2dl·(1l/10dl)=0’2l
0’2l·(1000cm3/1l)=200cm3
200cm3·(1000mm3/1cm3)=200000mm3
Cambios de unidades I:
1) Utilizando los factores de conversión realiza los siguientes cambios de unidades:
17 millas a kilómetros
3’2 pulgadas a centímetros
Ámbito Científico-Tecnológico
17 kilómetros a metros
17 litros a barriles U.S.
3500 mililitros a litros
5300 litros a metros cúbicos
250 miligramos a gramos
2000 kilogramos a toneladas
2 días a horas
7200 segundos a horas
4 años a días
300 hectáreas a kilómetros cuadrados
300 metros a kilómetros
5 galones U.S. a litros
3500 centímetros cúbicos a litros
1500 kilogramos a libras
4’5 kilogramos a gramos
17 libras a kilogramos
4 segundos a décimas de segundo
1200 décimas de segundo a minutos
300 acres a kilómetros cuadrados
1’21 kilómetros cuadrados a acres
Tablas de factores de conversión (igualdades)
Longitud:
centímetros (cm), metros (m). kilómetros (km).
1 metro cuadrado = 10000 centímetros cuadrados
1 kilómetro cuadrado = 0,3861 millas cuadradas
1 kilómetro cuadrado = 100 hectáreas
1 kilómetro cuadrado = 247,1 acres
1 kilómetro cuadrado = 1000000 metros cuadrados
Volumen:
litros (L), centilitros (cl), centímetros
cúbicos (cm3), decímetros cúbicos
(dm3), metros cúbicos (m3)
1 gramo = 1000 miligramos
1 kilogramo = 2,2046 libras
1 kilogramo = 1.000 gramos
1 kilogramo = 1000000 miligramos
1 tonelada = 1.000 kilogramos
1 tonelada = 1000000 gramos
Tiempo
1 centímetro = 0,3937 pulgadas
1 metro = 1,0936 yardas
1 metro = 3,2808 pies
1 metro = 39,370 pulgadas
1 metro = 100 centímetros
1 kilómetro = 0,6214 millas
1 kilómetro = 1000 metros
1 kilómetro = 100000 centímetros
Superficie:
kilómetro cuadrado (km2), metros
cuadrados (m2), centímetro cuadrados (cm2)
1 centímetro cúbico = 1 mililitro
1 litro = 0,26418 galones U.S.
1 litro = 100 centilitros
1 litro = 1000 mililitros
1 litro = 1 decímetro cúbico
1 litro = 1000 centímetros cúbicos
1 litro = 11,09556 barriles U.S.
1 metro cúbico = 1000 litros
1 metro cúbico = 264,18 galones U.S.
1 metro cúbico = 6,29 barriles U.S.
1 metro cúbico = 1000000 centímetros cúbicos
1 metro cúbico = 1000 decímetros cúbicos
Masa gramos (g), kilogramos (kg), miligramos (mg)
segundos (s), minutos (min), horas
(h), décimas de segundo (ds),
centésimas de segundo (cs)
Soluciones: 27’36 km, 8’13 cm, 17000m, 0’3 km,
188’62 barriles US, 18’93 L, 3’5 L, 3’5 L, 5’3 m 3,
3306’9 libras, 0’25 g, 4500 g, 2 toneladas, 7’7 kg, 48
h, 40 ds, 2 h, 2 min, 1461 días, 1’21 km2, 3 km2, 300
acres.
1 año = 365’25 días
1 día = 24 horas
1 día = 1440 minutos
1 hora = 60 minutos
1 hora = 3600 segundos
1 minuto = 60 segundos
1 minuto = 600 décimas de segundo
1 minuto = 6000 centésimas de segundo
1 segundo = 100 centésimas de segundo
Cambio de unidades II (cambios de prefijo):
Es importante que primero sepamos multiplicar potencias de igual base: xa·xb = x(a+b)
Para realizar estos cambios de unidades seguiremos el siguiente procedimiento:
1. Cambiar el prefijo que nos dan por la correspondiente potencia de base 10.
2. Introducir dos potencias de base 10, deberán de ser idénticas pero con el signo del
exponente cambiado y deberá de ser una de ellas la equivalente al prefijo que queremos
que aparezca.
Ámbito Científico-Tecnológico
3. Cambiamos la potencia por el prefijo que queremos que aparezca y multiplicamos las
potencias que nos queden.
Ejemplo: 14 nm a km
14 nm = 14·10-9 m = 14·10-9·10-3·103 m = 14·10-9·10-3 km = 14·10-12 km
1) Realiza los siguientes cambios de unidades:
a. 24 mm a nm
b. 3’78 dm a Gm
c. 0’0004 km a Mm
Soluciones:
1) 24·106 nm, 3’78·10-11 Gm, 0’0004·10-3 m
Cambios de unidades III (Cambios complejos):
1) Utilizando todo lo que sabes realiza los siguientes cambios de unidades (cambios
complejos):
50 km/h → m/s
10000 m2 → hectáreas
6 cm/s → km/h
3
3
8
6’13·10 kg/m → g/ml
3·10 m/s → km/s
9’8 m/s2 → km/h2
6’67·10-11 N·m2/kg2 → Din·cm2/g2 (dato: 1 N = 105 Din)
Soluciones:
1) 13’88 m/s, 1 hectárea, 0’216 km/h, 6’13 g/ml, 300000 km/s, 127008 km/h 2, 6’67·10-8 Din·cm2/g2.
Cambios de unidades IV (Nuevas magnitudes):
Datos extra
ENERGÍA: Unidad de medida en el S.I. (sistema internacional) el J (Julio).
Magnitud derivada: J = kg·m2/s2
¿Qué es la energía? Magnitud que nos mide la capacidad, que tiene aquellos sistemas
que midamos, para provocar cambios.
Qué es la energía cinética? Es la energía (capacidad para provocar cambios) debida al
movimiento que posee el sistema (un coche con velocidad, un columpio moviéndose…)
¿Qué es la energía potencial? Es la energía que posee un sistema debido a una
determinada configuración “cargada” (un muelle estirado, un objeto elevado que se
suelta, un arco pensionado, un hierro en la proximidad de un imán…)
Relaciones de igualdad:
1 cal = 4’186 J
1 kW·h = 3600000 J
1 erg = 10-7 J
1 electrón voltio (e.V.) = 1’6·10-19 J
1 Cal (Cal con mayúscula) =1 kcal
1 unidad térmica británica (BTU) = 1055 J
1 tonelada de equivalente de petróleo (tep) = 41’86 GJ
1) Utilizando los factores de conversión (igualdades) que relacionan unidades de
energía, realiza los cambios de unidades propuestos
Nota: si no tuviéramos la relación de igualdad entre las unidades implicadas pero
tuviéramos la relación de ambas con una tercera se realizará el cambio de unidades
pasando por esa tercera unidad.
34’6 J → cal
3456’17 cal → Cal
17 BTU → J
0’345 J → erg
23’098 kW·h → J
14·10-17 e.V. → J
Ámbito Científico-Tecnológico
Soluciones:
1) 8’266 cal, 3’45617 Cal, 17935 J, 3’45·10 6 erg, 8’31528·107 J, 2’24·10-35 J.
Datos extra
TEMPERATURA: Unidad de medida en el S.I. el K (kelvin). Magnitud fundamental.
¿Qué es la temperatura? La temperatura es una magnitud (propiedad que se puede
medir) que indica el grado de movimiento que tienen los corpúsculos de aquello que
medimos. Para ser más exactos, la temperatura nos indica la energía cinética media de
los corpúsculos que tiene un sistema.
¿Qué significan 0 K? A menos temperatura, menos movimiento de las partículas. Hay
una temperatura a la cual el movimiento ya no puede ser menor, porque las partículas
están paradas, esa temperatura es 0 K (o lo que es lo mismo, -273 ºC).
¿Cómo se cambia de unidades entre K (Kelvin) y ºC (grados centígrados o Celsius)?.
· Si tenemos ºC y queremos obtener K aplicaremos T (K) = T (ºC) + 273
Ejemplos (hazlos para comprobar que sabes hacerlo):
0 ºC = 273 K
53 ºC = 326 K
-63 ºC = 210 K
-305 ºC = imposible
· Si tenemos K y queremos obtener ºC aplicaremos T (ºC) = T (K) - 273
Ejemplos (hazlos para comprobar que sabes hacerlo):
0 K = -273 ºC
573 K = 300 ºC
163 K = - 110 ºC
- 53 K = imposible
1) Cambia de unidades:
a. 408 ºC  K
b. 32 ºC  K
d. 12 K  ºC
e. 246 K  ºC
Soluciones:
1)
a. 681 K
b. 305 K
c. 219 K
c. -54 ºC  K
f. 582 K  ºC
d. -261 ºC
e. – 27 ºC
f. 255 ºC
Datos extra
FUERZA: Unidad en el S.I. el N (Newton). Magnitud derivada, N = kg·m/s2
¿Qué es la fuerza? Es una magnitud que mide el grado de atracción o repulsión que
aparece entre dos cuerpos. En el lenguaje cotidiano las fuerzas típicas son: los choques
y golpes -son en realidad una repulsión- los tirones y sujeciones –son en realidad una
atracción.
Algunas relaciones de igualdad:
1 N = 105 dinas
1 N = 0’102 kilo fuerza (kilopondio)
1) Cambia de unidades:
a. 45 N  kilopondio
b. 56300000 Dinas  N
Soluciones:
1)
a. 441’17 kilopondios
b. 563 N
c. 3·104 N  Dinas
c. 3·109 Dinas (3 GDinas)
Datos extra
PRESIÓN: Unidad en el S.I. el Pa (Pascal). Magnitud derivada, Pa = kg / (m·s2).
Ámbito Científico-Tecnológico
¿Qué es la presión? Es una magnitud que nos relaciona la fuerza que siente una
determinada superficie.
¿Cómo se genera la presión en el interior de un fluido? Si introducimos un objeto en el
interior de un estado fluido (líquido o gas), como los corpúsculos (partículas que lo
constituyen) del fluido se trasladan de un sitio a otro , golpean la superficie del objeto.
Ese golpeteo que siente la superficie es la presión que está soportando el objeto
introducido en el fluido.
¿Qué relaciones de igualdad existen entre las unidades de la presión (proporcionalidad)?
1 atm = 101325 Pa
1 atm = 1013’25 mbar 105 Pa = 1 bar
1 atm =760 mmHg
(atm = atmósfera ; Pa = pascales ; bar = bares(mbar es milibares) ; mmHg = milímetros de mercurio)
1) Cambia de unidades:
a. 825 mmHg  atm
b. 300000 Pa  atm
d. 2’5 atm  Pa
e. 2000 mbar  Pa
Soluciones:
1)
a. 1´086 atm
b. 2’961 atm
c. 10 bar
c. 106 Pa  bar
f. 3 atm  mmHg
d. 253312’5 Pa
Ámbito Científico-Tecnológico
e. 2·105 Pa
f. 2280 mmHg