Turbulencia 1

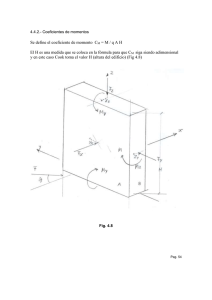
5.- TURBULENCIA
Debido a la rugosidad del terreno (árboles, montañas, edificios, etc.) se forman
remolinos o vórtices que perturban el flujo laminar y lo transforman en turbulento
(Fig. 52). Estos remolinos tienen tamaños entre 1 mm. y la altura gradiente.
Fig. 52
La energía cinética del flujo pasa a los vórtices grandes y es transferida a los menores
disipándose en calor, debido a la viscosidad del aire.
Se trata de un proceso en cascada, los torbellinos grandes se desagregan en torbellinos
menores (zona inercial) de equilibrio energético sin disipación de energía. Cuando
llegan los vórtices pequeños a la zona de disipación de energía se transforma en calor.
Hipótesis de Taylor : La estructura de los remolinos no cambia durante un tiempo
razonable.
Remolinos : D grande – frecuencia baja – velocidad alta – Re grande
D chico - frecuencia alta - velocidad baja – Re chico - la viscosidad
predomina
Llamemos V(z, t)la velocidad del viento y supongamos que actúa en el plano z,x
(fig. 53) y en función del tiempo y su origen esta fijado por la coordenada z. La
descomponemos en un valor medio V( z ) que es solamente función de z y un valor
V(z, t)que varía con t.
Fig. 53
Fig. 54
41
En este caso escribimos V(z, t)  V(z, t)  v(z,t)
Observamos que V(z) es constante con el tiempo y v(z,t) no.
 (z, t)
La velocidad fluctuante v(z,t)  V(z, t)  V(z)
 (z, t)
Si consideramos un sistema de eje en el espacio (1,2,3) y suponemos que V(z, t)no esta
incluido en ninguno de los tres planos 1-2, 1-3, 2-3 y V(z) es paralelo al plano 1-2
podemos descomponer  (z, t) en las componentes 1,2,3.(Fig. 55)

 3( z , t )
( z ,t )
1( z ,t )
 2( z ,t )
Fig. 55
V( z , t )  V( z )   ( z , t )
 ( z , t )   1( z ,t )   2( z ,t )   3( z ,t )
Podemos representar este mismo esquema , pero referido al vector posición r , con lo
cual la formula quedaría así :
V ( r ,t )  V ( r )   ( r ,t )
(47)
42
A su vez podemos descomponer V ( r ,t ) en dirección de los tres ejes: (Fig. 56)
 (r, t )   1(r ,t )  2(r ,t )  3(r ,t )
(48)
 3( r ,t )
V ( r ,t )
 ( r ,t )
r
V( r )
 1( r ,t )
 2 ( r ,t )
Fig. 56
A mayor velocidad de una ráfaga , menor será el tiempo de actuación y menor la
dimensión del vórtice sobre un edificio . Para que sea efectiva , debe envolver
completamente la construcción y su tamaño debe sobrepasar las dimensiones del
edificio , porque en los bordes del torbellino las velocidades disminuyen .
La Norma Británica establece la duración de la ráfaga en relación a la altura de la
construcción , para que sea efectiva :
3 seg. = 0 a 20 m. de altura.
5 seg. = 20 a 50 m. de altura.
20 seg. mayor de 50 m.
5.1 – Parámetros estadísticos
La magnitud que caracterizan la velocidad del viento constituyen un proceso aleatorio .
Proceso estacionario : Cuando los parámetros estadísticos (x , x , y1y , etc.) sobre el
total de registros posibles , son invariantes para cualquier modificación del origen de los
tiempos .
Proceso ergódico: Los parámetros estadísticos calculados sobre un conjunto de registros
posibles son iguales a los correspondientes calculados a lo largo del tiempo sobre
cualquier registro representativo del proceso .
Proceso estocástico : En un mismo punto , los parámetros estadísticos varían con el
tiempo.
Podemos suponer , como hipótesis simplificativa , que las fluctuaciones del viento
alrededor del valor medio constituyen un proceso estacionario ergódico , cuando
analizamos un registro único en el tiempo y se lo considera representativo de todos los
registros posibles .
43
Podemos así definir los siguientes parámetros estadísticos :
1 T
V ( z , t ) dt  V ( z , t )
T 0
Velocidad media : V( z ) 
(49)
1 T
2

V(z,t)  V(z)  dt

T 0
Varianza
σ V2 ( z ,t ) 
Pero
V(z,t)  V(z) = velocidad fluctuante =  ( z ,t )
2
V(z)

1
T

T
0
(50)
(51)
(z,2 t) dt  N (z,t)   = varianza de fluctuación de velocidad
2
= valor medio v
2
( z ,t )
Varianza de la componente de la fluctuación de velocidad .
 vi2 ( z ) 
1
T

T
0
 i(z,2 t) dt   i(z)2
i  1,2,3,...etc.
(52)
Varianza de las componentes v1 y v3.
 v21 v 3 
1 T 2
v 1(z,t) . v 32(z,t) . dt

0
T
(53)
Desviación Standard de la fluctuación de velocidad  v(z,t) 
2
 v(z,
t)
(54)
Fig. 57
44
La ecuación de Bernoulli para flujo laminar era :
½  V 2 + p =cte. y la presión dinámica : q = ½  V
Si consideramos las componentes de V en el espacio, y buscamos el valor medio de q :
q

1
 V12  V22  V32
2

(55)
Cuando no hay turbulencia (V1,V2 y V3 son valores ½ )
Por efecto de la turbulencia , debemos agregar otros términos .
La desviación Standard  N(z, t) es una velocidad, ya que indica la dispersión a partir de
un valor medio .
Como la velocidad fluctuante es un valor aleatorio, debemos introducir este parámetro.
Pero como en la ecuación (55) está elevada al cuadrado , se transforma en la varianza
(valor cuadrado medio)
Presión dinámica media turbulenta:
1
q   V12  V22  V32  v12( z ,t )  v 22( z ,t )  v32( z ,t )
2


(56)
2
El valor cuadrado medio N i( z ,t ) mide la energía de la fluctuación con i = 1,2,3,
n
Existen otros valores a considerar , como ser : v i2   Si (t) df
(57)
f: frecuencia de la vibración
Si: espectro de potencia : indica la contribución de la energía parcial contenida en cada
frecuencia
2
vi
Una medida de la turbulencia es la intensidad I 
V
(58)
5.2.- Tensiones de Reynolds
Habíamos visto que la viscosidad del fluido provocaba tensiones tangenciales
dv
l  
dz
(59)
45
Pero existe otra causa para producir tensiones tangenciales cuando hay
turbulencia(V>60 Km./h.) y es el intercambio de cantidad de movimiento entre capas
horizontales de aire .


 r  Tensión de Reynolds : - ρ . v1 . v 3  Momento turb ulentomedio
v 1  Componente de la velocidad fluctuante en direccióndel flujo (horizontal)
v 3  Componente en la direcciónperpendicular (vertical)
Cerca de la superficie, donde V  0 prevalecen las
La suma de ambas será :   1   r  

r
dV
  N1 N 3
dz

(60)
A mayor rugosidad del terreno mayor será : 
5.3.- Velocidad de fricción.
Consideremos una partícula de fluido y su trayectoria , referida a un sistema x y de
coordenadas .
De acuerdo a estudios realizados por Prandtl , aparece un parámetro llamado velocidad
de fricción. En el punto A , consideramos las componentes de la velocidad fluctuante
1 y 3 .

3

1
t g 
Fig. 58
 v (z)
z
 V  V (z )  V (z)
Debido a la turbulencia , la partícula de fluido en A se desplazara una distancia l en
dirección normal al escurrimiento , (donde la velocidad media es V(z) )
 "distanciade mezcla".
46
La diferencia de velocidades medias entre A y B será:
 V   tg  
V
z
(61)
Se supone que v1 y v3 son proporcionales y V es proporcional a las mismas:
v1  v 2
y


V
 v1 y v 3
z


V
 1
z
 V 
V V

 .  2 
vimos que:  r  . v1. v3 = . 


z
zz


2
r

r

=
V

z
 . v1 . v 3


2
V
3
z
 V 

=  



z


r
2
2
 *
(62)
(63)
Tiene dimensión de velocidad y fue llamada por Prandtl: Velocidad de Fricción.
No es una velocidad real , sino una abstracción aerodinámica para expresar en función
de la velocidad .
Pero por (63):
 *  v1 . v 3  f (rugosidad superficial y del gradiente de velocidad)
El valor de  no es afectado por la rugosidad y podemos escribir:   cte
V
  K1 . z
 *  K1z .
K 1  0,147 (valor experimental constante)
z
(64)
(65)
47