Concepto de flujo del campo eléctrico

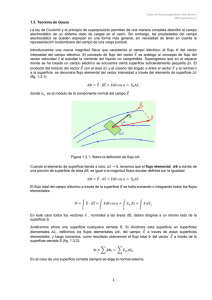
Concepto de flujo del campo eléctrico
Definimos en el tema anterior el flujo magnético a través de una
superficie como el número de líneas vectoriales (campo B) que la
atraviesan. De igual manera podemos definir flujo en un campo eléctrico
 = ∫ E dS
En el caso de que dicha superficie fuera cerrada:
 = ∫ E dS
Realizando la ecuación de dimensiones resulta que el flujo en el
sistema internacional se mide en voltio por metro (V.m).
Imaginemos una carga puntual Q, dentro de una superficie
cualquiera, si tomamos el centro de la carga podemos trazar una superficie
esférica cualquiera, de radio r. Las líneas de campo que atraviesan la
superficie esférica y la original son las mismas, por lo tanto ambas tendrán
el mismo flujo. Ahora bien, estas líneas son perpendiculares a la superficie
esférica, E y S igual dirección y sentido, y si el medio es homogéneo la
intensidad de campo eléctrico será la misma en todos los puntos de la
superficie, por lo que el flujo valdrá:
 = ∫ E dS = E ∫ dS = E 4πr2 = 4πr2 Q/ 4πέ r2 = Q/έ
En el caso de que dentro de la superficie existiesen varias cargas, Q,
Q, Q,… Q cada una de ellas creará su propio campo y, en consecuencia,
su propio flujo. El flujo total será la suma de los flujos individuales

QN / έ
expresión matemática del Th. De Gauss
El flujo neto que atraviesa una superficie cerrada (superficie
gaussiana) en un campo eléctrico es igual a la suma algebraica de las cargas
eléctricas encerradas en su interior dividida entre la constante dieléctrica
absoluta del medio en que se encuentran las cargas.
Esta ley puede interpretarse, en electrostática, entendiendo el flujo
como una medida del número de líneas de campo que atraviesan la
superficie en cuestión. Para una carga puntual es evidente que este número
es constante si la carga está contenida por la superficie y es nulo si esta
fuera (ya que hay el mismo número de líneas que entran como que salen).
Además, al ser la densidad de líneas proporcionales a la magnitud de la
carga, resulta que este flujo es proporcional a la carga, si está encerrada, o
nulo, si no lo está.
Cuando tenemos una distribución de cargas, por el principio de
superposición, sólo tendremos que considerar las cargas interiores,
resultando la ley de Gauss.
Sin embargo, aunque esta ley se induce de la ley de Coulomb, es más
general que ella, ya que se trata de una ley universal, válida en situaciones
no electrostáticas en las que la ley de Coulomb no es aplicable.
Problema: Una carga eléctrica puntual de + 2 μC se encuentra situada en
el centro geométrico de un cubo de 2 m de arista. El medio es el vacío.
Calcular: a) la intensidad de campo en el centro de una de las caras; b) el
flujo eléctrico a través de la superficie cúbica; c) el flujo eléctrico a través
de una de las caras. SOL: a) 1,8 104 N/C; b) 2,26 105 V.m; c) 3,77 104 V.m
Aplicaciones de la Ley de Gauss
Carga en un conductor:
En ausencia de campo eléctrico no puede haber corriente, ya que los
electrones han de moverse en un conductor por efecto de un campo
eléctrico, en este caso se dice que el conductor se encuentra en equilibrio
electrostático, eso significa que el campo eléctrico en su interior ha de ser
nulo. Si consideramos un conductor (macizo) cargado y en equilibrio se
puede demostrar fácilmente que la carga neta contenida en el interior del
conductor ha de ser nula (el campo eléctrico de cualquier punto interior ha
de ser nulo ya que está en equilibrio, la carga neta es nula). Por tanto la
carga, si el conductor está cargado, ha de estar localizada en la superficie.
Este hecho obliga a introducir el concepto de densidad eléctrica o
densidad superficial de carga, σ, que no es más que la relación entre la
carga y la superficie. La electricidad tiende a acumularse en las zonas de
mayor curvatura, en especial en las puntas, si la repulsión entre cargas es
suficientemente grande se origina el llamado viento eléctrico; por otra parte
el fenómeno llamado poder de las puntas (todo conductor provisto de
puntas se descarga rápidamente) es muy conocido por la pérdida enorme de
energía eléctrica que produce.
Campo eléctrico producido por un hilo conductor
indefinido
El teorema de Gauss afirma que
el flujo del campo eléctrico a
través de una superficie cerrada
es igual al cociente entre la
carga que hay en el interior de
dicha superficie dividido entre
0.
Para una línea indefinida
cargada, la aplicación del
teorema de Gauss requiere los
siguientes pasos:
1.-A partir de la simetría de la distribución de carga, determinar la
dirección del campo eléctrico.
La dirección del campo es radial y perpendicular a la línea cargada
2.-Elegir una superficie cerrada apropiada para calcular el flujo
Tomamos como superficie cerrada, un cilindro de radio r y longitud L.

Flujo a través de las bases del cilindro: el campo E y el vector
superficie S1 o S2 forman 90º, luego el flujo es cero.

Flujo a través de la superficie lateral del cilindro: el campo E es
paralelo al vector superficie dS. El campo eléctrico E es constante en
todos los puntos de la superficie lateral,
El flujo total es, E·2 rL
3. Determinar la carga que hay en el interior de la superficie cerrada
La carga que hay en el interior de la superficie cerrada vale q= L, donde 
es la carga por unidad de longitud.
4.-Aplicar el teorema de Gauss y despejar el módulo del campo
eléctrico
El mismo resultado que hemos obtenido previamente, pero de una forma
mucho más simple
Campo eléctrico producido par una carga distribuida
uniformemente sobre un plano
El plano tiene una carga por unidad de área. De la simetría se deduce que
las líneas son perpendiculares al plano. Tomando como superficie cerrada el
cilindro de la figura, solo habrá flujo a través de las tapas del cilindro de
área A. El flujo a través de una de esas tapas será EA. El flujo total será
por tanto EA. Por el teorema de Gauss sabemos que el flujo es:
Por tanto
EA
siendo Q=A Por consiguiente:
Campo eléctrico en el espacio comprendido entre dos
superficies planas paralelas que contienen cargas iguales y
opuestas.
En la región fuera de los dos planos los campos son iguales y de sentido
contrario y se anulan. En la región entre los planos los campos tienen el
mismo sentido y el campo será el doble que para el caso de un solo plano
1- Explicad cómo es el campo eléctrico y el potencial dentro, en la superficie, y en el
exterior de una esfera conductora cargada. (Abril 92)
2- Enunciad el Teorema de Gauss para el campo electrostático. En la figura adjunta,
calculad el flujo del campo a través de cada una de las tres superficies dadas. (Abril 92;
la Laguna, 89)
El vector superficie es un vector que tiene por módulo
el área de dicha superficie, la dirección es
perpendicular al plano que la contiene.
Cuando el vector campo E y el vector superficie S son
perpendiculares el flujo es cero.
El flujo del campo eléctrico a través de una superficie cerrada es igual a la carga total
encerrada dentro de la superficie dividido por la permitividad eléctrica del vacío ε0.
Su forma integral utilizada en el caso de una distribución extensa de carga puede
escribirse de la manera siguiente:
,
donde E es el campo eléctrico, dA es un elemento diferencial del área A sobre la cual se
realiza la integral, QA es la carga total encerrada dentro del área A y ε0 es la
permitividad eléctrica del vacío. Este teorema aplicado al campo eléctrico creado por
una carga puntual es equivalente a la ley de Coulomb de la interacción electrostática.
Este teorema fue enunciado por el matemático alemán Carl Friedrich Gauss en 1835,
pero no fue publicado hasta 1867. Debido a la similaridad matemática que tiene el
campo eléctrico con otras leyes físicas el teorema de Gauss puede utilizarse en
diferentes problemas de física gobernados por leyes inversamente proporcionales al
cuadrado de la distancia como la gravitación o la intensidad de la radiación. Este
teorema recibe el nombre de ley de Gauss y constituye también la primera de las
ecuaciones de Maxwell.
[editar]