Clase_cinética 3

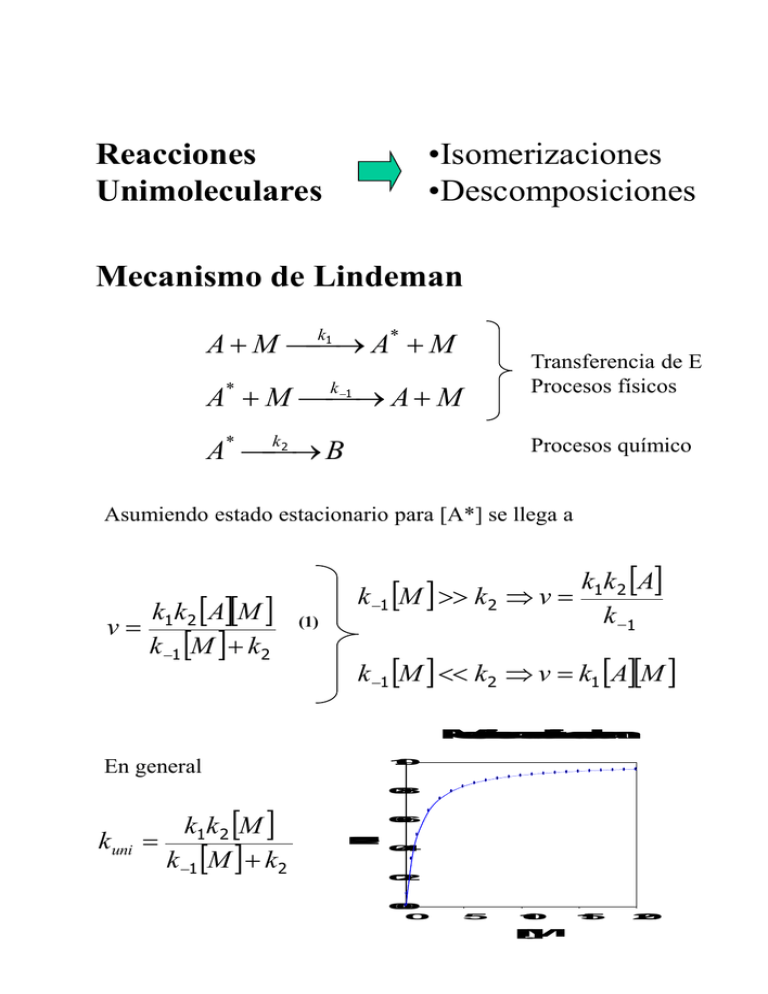
•Isomerizaciones
•Descomposiciones
Reacciones
Unimoleculares
Mecanismo de Lindeman
k1
A  M 
A*  M
k 1
A*  M 
A M
k2
A* 
B
Transferencia de E
Procesos físicos
Procesos químico
Asumiendo estado estacionario para [A*] se llega a
v
k1 k2 AM 
k 1 M   k2
k 1 M   k2  v 
(1)
k1 k2 A
k 1
k 1 M   k2  v  k1 AM 
M
e
c
a
n
i
s
m
o
d
e
L
i
n
d
e
m
a
n
En general
1
.
0
0
.
8
0
.
6
kuni
kuni
k k M 
 1 2
k 1 M   k2
0
.
4
0
.
2
0
.
0
0
5
1
0
[
M
]
1
5
2
0
Mecanismo de Michaelis-Menten
E  S  ES  E  P
(2)
Asumiendo estado estacionario para [ES] se llega a
v
d [ P] k1 k2 E S 

dt
k 1  k2
(3)
...pero se busca una expresión en función de [E]0=[E]+[ES]
v
k cat E 0
1  K M S 
(4)
k cat  k2 Nro. de intercambi o
KM 
k 1  k2
Cte. de Michaelis
k1
M
e
c
a
n
i
s
m
o
d
e
M
i
c
h
a
e
l
i
s
M
e
n
t
e
n
L v  k cat E 0  vmax
k E 
L v  cat 0 S 
S 0
KM
vS   K M   vmax 2
v
m
a
x
0
.
4
0
.
3
0
,
5
v
m
a
x
d[P]/t
S 
0
.
5
0
.
2
0
.
1
0
.
0
K
M
0
1
0
2
0
[
S
]
3
0
Linearización de la ec de M-M
k
v
v
 cat 
S E 0 K M K M E 0
(5)
v
S E 0
k cat
KM
m
1
KM
v
k cat
E 0
Inhibición
E  S  ES  E  P
E  I  EI
(7)
(6)
k cat E 0
v
KS 

I 
1 

1
S   K I 
Inhibición no competitiva
Activación
Competitiva
Reacciones
en cadena
•Combustiones
•Explosiones
•Polimerizaciones
Ej: Br2 + H2  2HBr
Br2  M  2 Br  M iniciación /terminaci ón
Br  H 2  HBr  H 
 propagación
H  Br  HBr  Br 
H y Br son portadores de cadena
d HBr 
 v2  v  2  v3
dt
Asumiendo estado estacionario para [ H ] y [ Br ]
d H 
 v2  v  2  v3  0
dt
d Br 
 2v1  2v1  v2  v2  v3  0
dt
Cadena ramificada. Ej: 2H2+O2  2H2O
H  O2  OH  O 

 ramificaci ón
O  H 2  OH  H 
