examen2

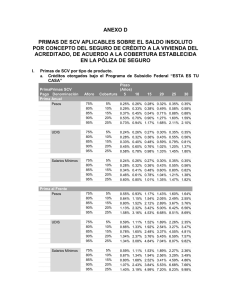
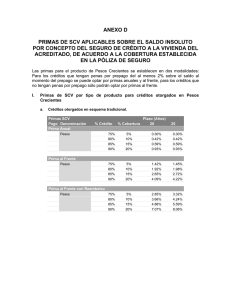
Segundo examen parcial de probabilidad.





Escribe tu nombre en cada una de las hojas del examen.
El examen consta de 2 secciones. Responde todas las preguntas de la sección A y cuatro de las
cinco preguntas de la sección B. Si respondes las cinco preguntas de la sección B se te tomarán
en cuenta las cuatro con la puntuación más alta.
Lee cuidadosamente cada pregunta antes de responderla.
Todas las preguntas deben ser respondidas en el examen. Puedes usar la parte de atrás de las
hojas para hacer cálculos. Si necesitas hojas adicionales, levanta la mano y solicítalas.
Si una pregunta se te dificulta, déjala y regresa a ella una vez que hayas respondido el resto del
examen.
¡Buena suerte!
Sección A
Circula el inciso que represente la respuesta correcta (sólo existe un inciso con la respuesta correcta).
(Cada pregunta vale 5 puntos. Valor total de la sección 35% )
1) ¿Cual de las siguientes variables es una variable discreta nominal?
a. Los estados de la república mexicana
b. El ingreso por hogar dividido en cuartiles
c. Edad
d. El porcentaje de votos para un partido político en distintas entidades federativas
e. La densidad de población.
2) ¿Cuál de las siguientes es una variable continua?
a. Afiliación religiosa
b. La edad dividida en estratos de cinco años (Ej. <5, 5 a 9, 10 a 14, 15 a 19 etc.)
c. La densidad de población
d. Doctrinas filosóficas
e. Las etapas de pañales para un bebé
3)
Las curvas que se muestran en el siguiente diagrama, describen las distribuciones de cuatro
diferentes variables. A partir de estas se puede inferir que:
a.
b.
c.
d.
e.
Todas son asintóticas excepto la 3
Todas tienen kurtosis negativa excepto la 3
Todas tienen sesgo positivo excepto la 3
Todas tienen la misma media excepto la 3
Todas tienen la misma desviación estándar excepto la 3

4) ¿Cuál de las siguientes distribuciones denotaría cómo se distribuye comúnmente el ingreso:
5) ¿Cuáles de los siguientes enunciados son falsos?
i. La distribución normal es simétrica y asintótica
ii. La distribución de Poisson se utiliza cuando un fenómeno ocurre de manera tan
común, que puede calcularse un promedio de ocurrencias
iii. La distribución binomial se utiliza sólo con variables discretas
iv. No existe forma de transformar una variable continua en una discreta.
a) i y ii
6) En la ecuación: Z 
a.
b.
c.
d.
e.
b) ii y iii
x  x
x
c) iii y iv
, Z representa:
5
x;   es igual a
x 4
b.
c.
d.
e.
e) ii y iv
La forma estandarizada de la media x
El número de desviaciones estándar a partir de la media en la cual se encuentra el dato x
El número de desviaciones estándar a partir de la media en la cual se encuentra el dato x
pero en términos cuadrados.
La raíz cuadrada del número de desviaciones estándar a partir de la media en la cual se
encuentra el dato x .
La varianza
7) La expresión:
a.
d) i y iii
e  4
4!
e  5
5!
e  4 e  5

4!
5!
e 3 e 4 e 5


3!
4!
5!
No puede decirse sin más información.


Sección B
Responde 4 de las 5 preguntas de esta sección mostrando tus operaciones.
Cada inciso vale 8 puntos (1 por responder, 4 por el desarrollo y 3 por obtener la respuesta correcta)
(Valor total de la sección 65%)
Formulario
n  x nx
bx; n, p    p  q
x 
8)
9)
e   x
n!
bx; n   x; np
Z
x  x
x
El tiempo medio de recorrido al trabajo en la Cd. De México es de 60 minutos con una desviación
estándar de 20 minutos mientras que en Guadalajara, el tiempo medio de recorrido al trabajo es de
30 minutos con una desviación estándar de 15 minutos. Si se supone normalidad en esta variable:
a. ¿Qué es más probable, que una persona haga entre 30 y 45 minutos al trabajo en la ciudad
de México, o que una persona haga entre 40 y 60 minutos al trabajo en Guadalajara?
b.

 x;  
¿Qué porcentaje de personas realizan viajes al trabajo, en la ciudad de México, de más de
noventa minutos?

Es extremadamente difícil predecir las inundaciones graves en cierta región del sureste mexicano.
Sin embargo, durante los últimos 400 años, desde que se han cuantificado, se han registrado un
promedio de 5 inundaciones graves por lustro. Cual es la probabilidad de que
a. ¿En el próximo lustro haya exactamente 5 inundaciones graves en esta región?
b.
¿En un lustro cualquiera lustro haya al menos 5 inundaciones graves?
10) 80% de los habitantes del municipio de Urique son indígenas. Si se seleccionan a 10 personas de
este municipio aleatoriamente, ¿cuál es la probabilidad de que:
a. entre 3 y 4 sean indígenas?
b.
hasta el 50 por ciento sean indígenas?
11) La probabilidad de que una persona viva más de 70 años es de 1/3. De una muestra aleatoria de
20 personas,
a. cual es la probabilidad de que las 20 vivan más de 70 años
b.
i. Utiliza la aproximación de Poisson, a la binomial para calcular el inciso ‘a’
ii. ¿Confiarías en esta segunda estimación? ¿Por qué?
12) Se puede suponer que el número de miembros de las familias mexicanas que viven en ciudades de
más de 1,000,000 de habitantes es una variable con una distribución cercana a la normal. Si la
familia promedio tiene 5.2 miembros con una desviación estándar de 1.5 miembros, ¿qué
porcentaje de estas familias tienen
a. entre 3 y 6 miembros?
b.
Si sólo se conociese la media, ¿podría suponerse una distribución de Poisson para estimar
una probabilidad de ocurrencia? ¿Por qué?