prueba 2 -taller tres stat 555

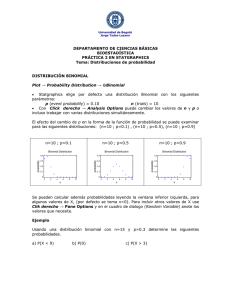
Programa AHORA
Estadística 555
Facilitadora: Sylvia Y. Cosme Montalvo
Taller tres – Dispersión, Distribuciones de Frecuencia Discretas y Continuas
Nombre: Jennifer Vélez Claudio
Fecha: 9 de julio de 2015
Prueba 2
Instrucciones generales: Seleccione uno de los dos ejercicios de distribuciones Binomial (entre 2
y, 4), Poisson (entre 3 y 5). El ejercicio 1 debe realizarlo. Puede utilizar Excel y hacer entrega
digital, si lo prefiere. También, puede trabajar los ejercicios de forma colaborativa. Cada ejercicio
tiene un valor de 20 puntos.
1. Los siguientes datos presentan el gasto de compra de alimentos en una base semanal para
una muestra de entrevistados que acudieron a un supermercado en el Área
Metropolitana
$96 $100 $116 $123 $134 $141 $150 $151 $159 $162 $170 $177 $181
$188 $190 $192 $199 $205 $227 $231 $232 $235 $240 $246 $250 $266
$271 $278 $279 $279 $279 $294 $295 $297 $303 $309 $319 $320 $321
$325 $335 $337 $337 $342 $363 $427 $429 $434 $474 $570
a)
Determine las medidas de variación.
 Rango = 474
 Varianza= 10,215.56
 Desviación Estándar de la muestra= 101.07
 Coeficiente de Variación = 39% Formula =Desviación estándar / media
 Rango Intercuartil = 140.25
 Media= 266
 Moda = 279
 Mediana= 258
b)
A base de los cálculos obtenidos, ¿qué puede decir del gasto en compra semanal?
A base de los cálculos obtenidos podemos decir que según la media de $259 que
es el promedio semanal de gastos es alto al igual que la desviación estándar de la
muestra.
2. El departamento de control de calidad de una empresa que fabrica bolígrafos sabe que el
5% de su producción tiene algún tipo de defecto. Los bolígrafos se empaquetan en cajas
con 15 elementos. Calcular la probabilidad de que una caja contenga:
a. 2 elementos defectuosos.
=BINOM.DIST(B5,B4,B2,FALSE)
=0.134752297
p=
0.05
n=
15
X=
2
P (X=2)
0.134752
b. Menos de 3 elementos defectuosos.
=1-BINOM.DIST(B12,B11,B9,TRUE)
= 0.0055
p=
n=
X=
P (X=3)
0.05
15
3
0.0055
c. Entre 3 y 5 elementos defectuosos
=BINOM.DIST(B19,B18,B16,TRUE)
= 0.9945
p=
n=
X=
P (X=3)
0.05
15
3
0.9945
3. La probabilidad de que el Banco del Pueblo reciba un cheque sin fondos es 1%.
a. Si en una hora reciben 20 cheques, ¿cuál es la probabilidad de que se tenga algún
cheque sin fondos?
=POISSON.DIST(G3,G2,TRUE)
Promedio =
0.01
X=
P(X=0) =
1
1.00
b. Si se computaran los primeros 500 cheques, ¿cuál es la probabilidad de recibir
entre 3 y 6 cheques sin fondos?
=POISSON.DIST(G3,G3,TRUE)
Promedio =
X=
P(X=0) =
0.01
6
0.61