5.3 - Clip2Net

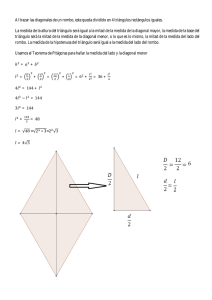
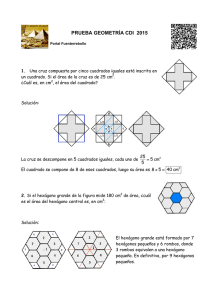
Plan de clase (1/4)
Escuela: _______________________________________ Fecha: _____________
Profr.(a): _____________________________________________
Curso: Matemáticas I
Apartado: 5.3
Eje temático:
FEM
Conocimientos y habilidades: Resolver problemas que impliquen el cálculo de áreas
en diversas figuras planas y establecer relaciones entre los elementos que se utilizan
para calcular el área de cada una de estas figuras
Intenciones didácticas: Que los alumnos establezcan relaciones entre los elementos
de la fórmula para calcular el perímetro o el área del rectángulo.
Consigna: En equipo resuelvan el siguiente problema.
El perímetro de un terreno rectangular mide 120 metros y el ancho mide 18 metros.
¿Cuánto mide el largo del terreno?
Consideraciones previas:
Es probable que algunos alumnos se confundan y simplemente resten 18 a 120 para
calcular la medida que se pide. Sin embargo también es probable que ellos mismos se
den cuenta del error y lo corrijan. Se espera que la mayoría considere las relaciones
entre los elementos de la fórmula para calcular el perímetro del rectángulo, aunque sólo
a través de cálculos aritméticos, es decir, que resten dos veces 18 a 120 y el resultado
lo dividan entre dos. En el mejor de los casos, pueden expresar la fórmula: 2a + 2l =
120 (dos veces el ancho, más dos veces el largo es igual a 120), después sustituir la a
por 18 y resolver la ecuación. Si se cree conveniente se les puede proponer este
desarrollo y probarlo con un problema similar, pero sólo después de que ellos
encuentren la solución con sus propios medios.
Si queda tiempo se continúa en la misma sesión con el siguiente problema: El área de
un terreno rectangular mide 526 m2 y su ancho mide 20m. ¿Cuánto mide el largo?
También en este caso hay que dejar que ellos resuelvan y después, en caso necesario,
traer a colación la fórmula para analizar los datos que se tienen y la ecuación a
resolver.
Observaciones posteriores:
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
Plan de clase (2/4)
Escuela: _____________________________________
Fecha: _____________
Profr.(a): _____________________________________________
Curso: Matemáticas I
Apartado: 5.3
Eje temático: FE y M
Conocimientos y habilidades: Resolver problemas que impliquen el cálculo de áreas
en diversas figuras planas y establecer relaciones entre los elementos que se utilizan
para calcular el área de cada una de estas figuras
Intenciones didácticas:
Que los alumnos calculen el valor faltante en perímetros y áreas de triángulos y
cuadriláteros.
Consigna 1: Cada equipo resuelva uno de los siguientes problemas.
1) ¿Cuánto mide la altura de un trapecio cuyas bases miden 76 cm y 36 cm y su
área es de 392 cm2?
2) ¿Cuál es el área de un rombo cuya diagonal mayor es cinco unidades más
grande que la diagonal menor y ésta mide 7.5 cm?
3) ¿Cuánto mide la altura de un triángulo cuya área es 24 dm 2 y su base mide el
triple de la longitud de la altura?
4) ¿Cuánto mide el lado de un cuadrado cuyas diagonales miden 30 mm cada
una?
Consideraciones previas:
Aquí es importante analizar las diversas estrategias de solución que presenten los
alumnos para resolver cada problema y posteriormente analizar lo que pasa con las
fórmulas, de manera que este contenido quede fuertemente vinculado al estudio de las
ecuaciones. En el caso del último problema, si no recuerdan que un cuadrado también
es un rombo, habrá que ayudarlos recordando la definición de estos cuadriláteros.
En caso de que haya tiempo después de analizar los problemas anteriores se pueden
trabajar los siguientes, o bien, dejarlos de tarea.
a) El área de un triángulo es de 27 cm2 y su altura de 9 cm, ¿cuánto mide la base?
b) El área de un romboide es de 420 cm2 y su base mide 28 cm, ¿cuánto mide su
altura?
c) Un trapecio tiene 1200 mm2 de área; su lado mayor mide 56 mm y el menor 40
mm. ¿Cuál es su altura?
d) ¿Cuál es el área de un rombo cuya diagonal mayor mide el doble de la diagonal
menor y la longitud de ésta es de 7.5 cm?
Observaciones posteriores:
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
________________________________
Plan de clase (3/4)
Escuela: _________________________________________
Fecha: _________
Prof. (a): _________________________________________________________
Curso: Matemáticas I
Apartado: 5.3
Eje temático: FE y M
Conocimientos y habilidades: Resolver problemas que impliquen el cálculo de áreas
en diversas figuras planas y establecer relaciones entre los elementos que se utilizan
para calcular el área de cada una de estas figuras.
Intenciones didácticas:
Que los alumnos utilicen las fórmulas para calcular el área del cuadrado y del círculo, al
resolver problemas.
Consigna. En equipos de tres integrantes, resuelvan los siguientes problemas:
1. Se dispone de una tabla de madera de forma cuadrada, como se muestra en la
figura, a la cual se le pretende dar una forma circular para que sirva de tapa de un
recipiente que tiene forma cilíndrica.
3.5 cm
a) ¿Qué área de la madera se va a usar?
b) ¿Cuál es el área de la madera que no se va a utilizar?
2. ¿Cuál es el área de la parte sombreada de la siguiente figura, si el radio del círculo
mide un metro? Justifiquen su respuesta.
Consideraciones Previas:
Probablemente la mayoría de los alumnos no recuerden la fórmula del área del círculo,
el maestro podrá solicitar si alguien del grupo la recuerda, si es así, que la dé a
conocer. Por otra parte se permitirá el uso de la calculadora, usando valor de pi con
dos cifras decimales (3.14)
Consideraciones Posteriores:
______________________________________________________________________
______________________________________________________________________
Plan de clase (4/4)
Escuela: ________________________________________
Fecha: __________
Prof. (a): _____________________________________________________________
Curso: Matemáticas I
Apartado: 5.3
Eje temático:
FE y M
Conocimientos y habilidades: Resolver problemas que impliquen el cálculo de áreas
en diversas figuras planas y establecer relaciones entre los elementos que se utilizan
para calcular el área de cada una de estas figuras.
Intenciones didácticas:
Que los alumnos utilicen las fórmulas para calcular el área del triángulo y del cuadrado,
al resolver problemas.
Consigna. En equipos de tres integrantes, resuelvan el siguiente problema:
La siguiente figura representa el vitral de una ventana cuadrada que está formada por
varios cuadrados más pequeños. La parte del vitral que tiene forma triangular es de
color rojo y se quebró el vidrio de la parte sombreada.
M
1m
M
Al tratar de reparar el vitral:
1. ¿Cuántos cm2 de vidrio rojo deberá utilizar quien la repare?
2. ¿Cuántos cm2 de vidrio rojo usa este vitral?
3. ¿Qué fracción del área total representa el triángulo rojo?
Consideraciones Previas:
Se espera que los equipos encuentren al menos una de las formas posibles para
encontrar el área solicitada (cálculo directo del área del triángulo sombreado,
deducción que es la cuarta parte y diferencia de áreas).
Puede que algún alumno diga que falta un valor, en este caso el maestro debe hacer
énfasis en que M es el punto medio.
Se debe tener cuidado, si se presenta la confusión sobre la altura del triangulo
sombreado con respecto a la altura del cuadrado o de los otros triángulos.
En caso de que el problema resulte demasiado fácil y la mayoría de los equipos
encuentren la solución; se puede plantear la siguiente variante del problema:
La siguiente figura representa una ventana de forma cuadrada que es parte de otro
vitral:
M
N
3dm
M es el punto medio del lado.
N es el punto medio entre M y el vértice.
Contesta las siguientes preguntas:
1. ¿Cuál es el área de cada uno de los triángulos sombreados?
2. ¿Qué representa el área de los triángulos sombreados con respecto al cuadrado
completo?
Consideraciones Posteriores:
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________