GUIA “CERO” DE MAT 178 ( 2º Sem

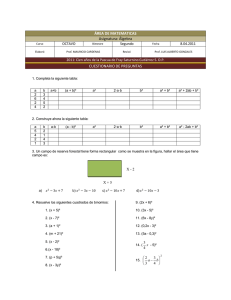
GUIA “CERO” DE MAT 178 ( 2º Sem. 2010)
MATERIA.- Algebra básica y otros complementos colegiales.
I.- Ejercicios misceláneos sobre evaluación numérica:
Calcule el valor de x
1.) x 2b
2.) x 
3a  b
a2  b2
 2a  4b 5a  b 


 si a=1/3 , b=-1/2
 3a  3b a  b 
u u u
, si u=2
1
1 u u
 1
2
1
1 
 , si a =-8
3.) x 
 4 4


2
1 a
 a  1 4a  4 4(a  1) 
4


4.) x   1  1  1 


3
3
5.) x  a  3(a  b)  3(a  2b) 3  (a  3b) 3 , si a= 60 y b = 0.15a
b2
ab
b
a , si a = 15/4 y b = 0.84a

6.) x 
2a
a2
ab
b
II) Ejercicios de Simplificación
Simplifique “a finish” e indique los valores “prohibidos” para las variables.
1
(a 2  b 2 )
ab
1.)
 a  b 
1  1  
 b  a 
2.) ( 3 a  1  3 b  1)( 3 (1  a)2  3 1  a  b  ab  3 (1  b)2 )
ab
ab
 2a
 2a
4ab
a

b
a

b


3.)
ab
ab
a 2b 2
2b 
2b 
4b 2 
ab
ab
( a  b) 2
4.)
bc
ac
ab
2abc



(a  b)(a  c) (b  c)(a  c) (a  c)(b  c) (a  b)(a  c)(b  c)
 xy
 x  y x  y  x 2  y 2

5.) 

 1 2
2
 x  y x  y  2 xy
x y
( x  y) 3  ( x 3  y 3 )
6.)
xy( x  y)
a 2  b 3 a 2  b 2 a 2 b  ab2

 2
2a  2b 2a  2b
a  b2
m
1 
 m  2 m 1
 m  1
8.) 1 

 2m



m
m 1

 m  1 m  2 2m  1
7.)
III Simplifique, de modo que no queden exponentes negativos ni fraccionarios.

1.- 2ab (a  2b  2 7 )  2  457 a 4b 3 (a) b3 
1.

2 1 / 5

2.- (a 1 / 3  b1 / 3 )(4a 1 / 3  b1 / 3 )  (23 a  3 b ) 2
3.-
(a1 / 2  a 1 / 2 ) 2
 (2 a ) 
a 1
4.-
(a 2  2ab  b 2 ) 3  (a 2  2ab  b 2 ) 3
2
2ab
2ab
 a 2
2
b 1
b 1
2ab
2ab
a 2
 a 2
b 1
b 1

2
(a  1)
(a  b  0)
a
5.-
(a  0  b  1)
IV Ejercicios sobre proporciones y porcentajes
3a 2  ab  b 2
1.- Si a : b = 2 : 3 y k 
expresar a en tanto % de k.
3a  2b
2.- Para la altura del centro de gravedad de un tronco de cono, rige la formula
siguiente:
R 2  2Rr  3r 2
z
·b
4( R 2  Rr  r 2)
¿Qué tanto % de b mide Z, si r mide 50% de R?
2ab  3ac  2bc
3.- Si a : b : c = 5 : 3 : 13 y r 
, expresar r en tanto % de b
abc
4.- Si a : b = 7 : 11 y b : c = 9 : 13 y expresar a en tanto % de c.
5.- Si x : y = 5 : 8 ¿Qué tanto % de y mide la quinta parte de x?
6.- Si a : b : c = 5 : 6 : 7 ¿qué tanto % de (b + c) mide (a + b)?
7.- En un triangulo rectángulo se sabe que el cateto mayor mide 96% de la
hipotenusa; ¿Qué tanto % de la hipotenusa mide el cateto menor?
8.- Calcular el perímetro de un triángulo cuya hipotenusa mide 3 metros, si un
cateto mide 40% más que el otro.
9.- Una esfera mide 8 centímetros de radio; ¿qué tanto % de superficie mide el
área de uno de círculos máximos?
10.- Se divide un terrero en partes desiguales; de la parte menor vende el 31 % y
de a parte mayor el 95%, quedándose con el 21% del terreno primitivo. ¿Qué tanto % de
la parte mayor mide la parte menor?
11.- Si un triángulo ABC el lado a mide a 2/3 del semiperímetro s, mientras que
b es igual a la mitad de s; ¿qué tanto % de c mide b?
12.- ABCDE sea un pentágono regular inscrito en una circunferencia de centro
O y de radio OA = 87 [cm]. ¿Qué tanto % del área del círculo mide el área del menor de
los dos sectores circulares determinados por OA y OC?
13.- La longitud de un trozo de caucho disminuye en 20 % por compresión; al
soltarlo aumenta su longitud en 20 % ¿qué tanto % ha variado su longitud primaria?
14.- La potencia de un circuito está dad por N  I 2 R[W ] donde:
U
I  [ A]
R
¿Qué tanto % varia la potencia N, si la tensión U disminuye en 15%?
15.- La ley de Newton nos da: F = m · a ¿Qué tanto % aumenta la aceleración a,
si la fuerza aumenta 2% y la masa disminuye en 4%?
16.- Si el radio basal de un cono circular recto aumenta en 15%, mientras que su
altura disminuye en 20%, ¿qué tanto % varían:
a) La superficie basal del cono,
b) La superficie total del cono y
c) El volumen del cono?
17.- ¿En qué tanto % debe disminuirse el radio de una esfera para que su
superficie disminuya el 19%?
18.- ¿En qué tanto % hay que aumentar el radio de una esfera, para que su
volumen aumente un 33,1%?
19.- Si cada arista de un cubo aumenta en 8%, ¿qué tanto % aumenta el
volumen del cubo?
20.- Si cada lado de un triángulo isósceles disminuye en 18%, ¿en qué tanto %
disminuye el área del triángulo?
21.- ¿En qué tanto % debe variarse la distancia entre dos polos magnéticos del
mismo signo que la fuerza de repulsión entre ellos aumente en 21%?
22.- Sobre el lado CD de un cuadrado ABCD de 0,4[m 2 ] de área se ha
determinado un punto G, tal que DG : GC = 3 : 1; desde B se ha bajado la perpendicular
AG ¿cuánto mide esta perpendicular?
23.-Una pirámide de base cuadrada tiene todas sus aristas basales y laterales de
60 [cm] ¿cuántos dm3 mide su volumen?
24.- El ancho de un anillo circular mide 8% más que el radio r de la
circunferencia interior, ¿qué tanto % del área del anillo mide el círculo interior si su
diámetro es de 70 [cm]?
V Factorización
Factoriza las siguientes expresiones algebraicas:
1) 64  b12
2) 6 xy  2 xz  8 yz
3) 18x 3 y  9x 2 y  27x 2 y 2
5) x 6  y 6
7) 4x 2 y 2  ( x 2  y 2  z 2 ) 2
2
2
9) 4x  4xy  y  18x  9 y  18
4) 27a 3  125b 3
6) (2x  1) 2  8(2x  1)  16
8) m3  n 3  m 2  mn  n 2
3
3
3
10) x  y  z  3xyz
3
3
3
3
11) ( x  y  z)  x  y  z
VI Ecuaciones y Sistemas de Ecuaciones
1.- Sean 
y  las raíces de la ecuación
6
10
7


0
X 1 X  2 X  3
Calcule   
2.- Ahora  y  son las raíces de :
91x  2
1
x 2  200
Calcule
3.- Sean r
y
(   )
  1

s las raíces de 6 x 2  5 x  1  0 . Encuentre otra ecuación de 2º grado tal
3
y s 3
que sus raíces sean r
2
2
2
2
4.- Las raíces de  y  de la ecuación x  3ax  a  0 , son tales que    
Calcule el valor de a.
7
4
Resuelva los siguientes sistemas de ecuaciones:
5.-
x y
 2
b a
x y
1
   (a  b)( a  2)
a b
ab
6.-
x y 1
 ( x  y  2)  4
8
3
3( x  y) 2  12
7.-
5 x  6 y  98
5 x  6 y  158
8.-
x3  y 3  1
x 3 y  2xy 2  y 3  2
9.-
x 2  xy  y 2  4
x y 2
10.-
( x 2  1)( y 2  1)  10
( x  y)(xy  1)  3
11.-
Indicación:
xy  u

x y v
x( y  z )  4
y( x  z )  9
z ( x  y)  16
12.- En el ejercicio siguiente no se pide hallar las soluciones, sino probar que existe un
nº par de soluciones:
( y 2  6)(x  1)  y( x 2  1)
( x 2  6)( y  1)  x( y 2  1)