Problemas de Geometría

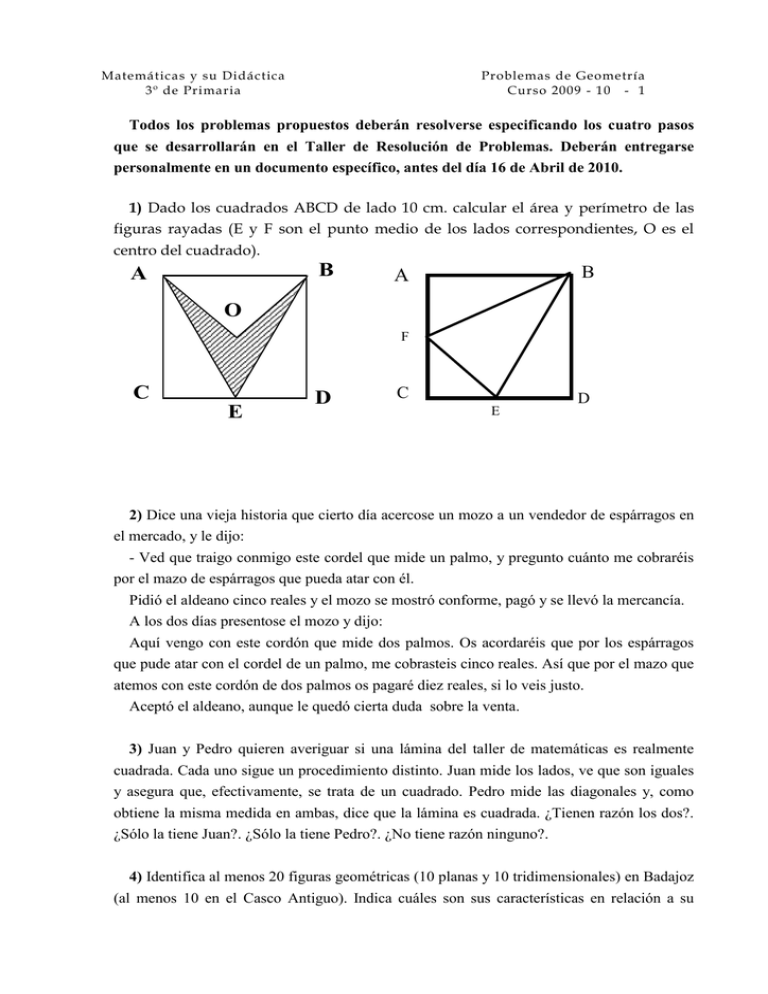
Matemáticas y su Didáctica
3º de Primaria
Problemas de Geometría
Curso 2009 - 10 - 1
Todos los problemas propuestos deberán resolverse especificando los cuatro pasos
que se desarrollarán en el Taller de Resolución de Problemas. Deberán entregarse
personalmente en un documento específico, antes del día 16 de Abril de 2010.
1) Dado los cuadrados ABCD de lado 10 cm. calcular el área y perímetro de las
figuras rayadas (E y F son el punto medio de los lados correspondientes, O es el
centro del cuadrado).
B
A
B
A
O
F
C
E
D
C
E
D
2) Dice una vieja historia que cierto día acercose un mozo a un vendedor de espárragos en
el mercado, y le dijo:
- Ved que traigo conmigo este cordel que mide un palmo, y pregunto cuánto me cobraréis
por el mazo de espárragos que pueda atar con él.
Pidió el aldeano cinco reales y el mozo se mostró conforme, pagó y se llevó la mercancía.
A los dos días presentose el mozo y dijo:
Aquí vengo con este cordón que mide dos palmos. Os acordaréis que por los espárragos
que pude atar con el cordel de un palmo, me cobrasteis cinco reales. Así que por el mazo que
atemos con este cordón de dos palmos os pagaré diez reales, si lo veis justo.
Aceptó el aldeano, aunque le quedó cierta duda sobre la venta.
3) Juan y Pedro quieren averiguar si una lámina del taller de matemáticas es realmente
cuadrada. Cada uno sigue un procedimiento distinto. Juan mide los lados, ve que son iguales
y asegura que, efectivamente, se trata de un cuadrado. Pedro mide las diagonales y, como
obtiene la misma medida en ambas, dice que la lámina es cuadrada. ¿Tienen razón los dos?.
¿Sólo la tiene Juan?. ¿Sólo la tiene Pedro?. ¿No tiene razón ninguno?.
4) Identifica al menos 20 figuras geométricas (10 planas y 10 tridimensionales) en Badajoz
(al menos 10 en el Casco Antiguo). Indica cuáles son sus características en relación a su
Matemáticas y su Didáctica
3º de Primaria
Problemas de Geometría
Curso 2009 - 10 - 2
forma y dimensiones aproximadas.
5) Calcular el área y perímetro del triángulo rectángulo de la figura
6) Los lados de un rectángulo se prolongan en un 5% de su longitud. ¿En qué porcentaje
crece el perímetro? ¿Y el área?.
7) Identificar los polígonos de la figura y sus propiedades, estableciendo relaciones entre
ellos.
El lado del hexágono interior vale 6
u.
8) Miguel quiere comprar dos paquetes de pipas de 0,15 euros cada uno y tres barras de
regaliz, también de 0,15 euros, ¿Cuánto le quedará si tiene 2 euros?
Matemáticas y su Didáctica
3º de Primaria
Problemas de Geometría
Curso 2009 - 10 - 3
1 cm.
9) Calcular el área de la
figura amarilla
10) Dibuja dos triángulos isósceles cuyas áreas sean una el doble que la otra. Dibuja dos
triángulos isósceles cuyo perímetro sea uno sea el doble que el del otro. Repite el problema
con un hexágono regular.
11) Une los puntos medios de los lados consecutivos de un cuadrilátero y analiza la figura
resultante.
12) Intenta encontrar un método claro que te permita contar “todos” los triángulos y
rectángulos que aparecen en las figuras. Luego, dices cuántos hay, de qué tipo, cómo los has
contados y por qué tienes la certeza de que no falta ninguno.
13) En la figura E, F, G y H son los puntos medios de los lados del cuadrado ABCD. ¿En
qué proporción está el área del cuadrado interior respecto al área del cuadrado ABCD?
Matemáticas y su Didáctica
3º de Primaria
E
A
H
D
Problemas de Geometría
Curso 2009 - 10 - 4
B
F
G
C
14) Escribir y justificar tres estrategias diferentes para resolver el siguiente problema
“La diagonal de un cuadrado mide 14 cm. Calcular su área y perímetro.
15) “Calcular el área y perímetro de las figuras que resultan al unir tres cuadrados cuyos
lados miden 3 cm.”