Curso 00/01 (Convocatoria de Septiembre)

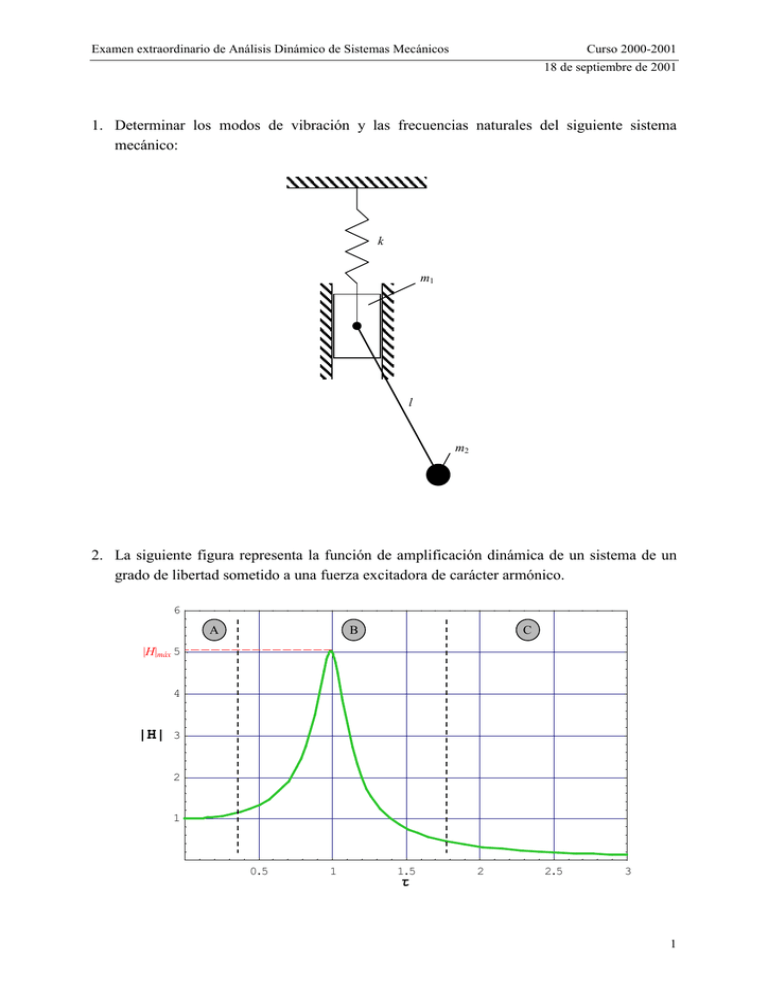
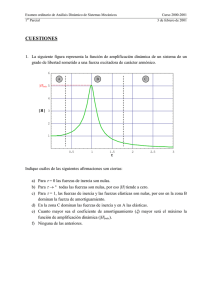
Examen extraordinario de Análisis Dinámico de Sistemas Mecánicos
Curso 2000-2001
18 de septiembre de 2001
1. Determinar los modos de vibración y las frecuencias naturales del siguiente sistema
mecánico:
k
m1
l
m2
2. La siguiente figura representa la función de amplificación dinámica de un sistema de un
grado de libertad sometido a una fuerza excitadora de carácter armónico.
6
A
B
C
|H|máx 5
4
»H»
3
2
1
0.5
1
1.5
τ
2
2.5
3
1
Examen extraordinario de Análisis Dinámico de Sistemas Mecánicos
Curso 2000-2001
18 de septiembre de 2001
Indique cuáles de las siguientes afirmaciones son ciertas:
a) Para τ = 0 las fuerzas de inercia son nulas.
b) Para τ → ∞ todas las fuerzas son nulas, por eso |H| tiende a cero.
c) Para τ = 1, las fuerzas de inercia y las fuerzas elásticas son nulas, por eso en la zona B
dominan la fuerza de amortiguamiento.
d) En la zona C dominan las fuerzas de inercia y en A las elásticas.
e) Cuanto mayor sea el coeficiente de amortiguamiento (ξ) mayor será el máximo la
función de amplificación dinámica (|H|máx).
f) Ninguna de las anteriores.
3. El transporte de una mercancía delicada exige que esta no golpee en ningún momento
contra su contenedor y que su aceleración (absoluta) no sobrepase en ningún momento la
del contenedor. Se sabe que el contenedor está sometido a un movimiento vertical (y(t)),
armónico y monocromático, de amplitud Y= 30 mm y frecuencia f= 0,5 Hz. Si la masa de
la mercancía es m= 500 kg y la holgura mínima vertical es de δ= 20 mm, diseñe,
razonadamente, el sistema de suspensión (c, k). (3 Ptos.)
δ
m
k
c
y(t)
Las ecuaciones de un sistema sometido a movimiento de la base son:
X
=
Y
Z
=
Y
1 + 4ξ 2τ 2
(1 − τ )
2 2
+ 4ξ 2τ 2
τ2
(1 − τ )
2 2
+ 4ξ 2τ 2
Donde X es la coordenada que expresa el movimiento absoluto y Z el movimiento
relativo al de la base.
2
Examen extraordinario de Análisis Dinámico de Sistemas Mecánicos
Curso 2000-2001
18 de septiembre de 2001
4. En el sistema de la figura, la fuerza transmitida a la base viene dada por la expresión:
a) m( x − y)
F(t)
b) kx
x(t)
c) k ( x + y ) + F (t )
m
d) F (t ) − m( x − y)
e) Ninguna de las anteriores
k/2
k/2
y(t)
Tiempo: 1 hora
3