Tema II: Análisis
Anuncio

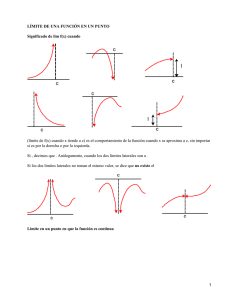
Tema II: Análisis Límites En matemáticas, se usa el concepto del límite para describir la tendencia de una sucesión o una función. La idea es que en una sucesión o una función, decimos que existe el límite si se puede acercar a un cierto número (o sea, el límite) tanto como queramos. Se usa el límite en cálculo (por lo que también se usa en el análisis matemático) para definir convergencia, continuidad, derivación, integración, y muchas otras cosas. Límite de una función: El límite de la función f(x), cuando x tiende a p es un número L, con la propiedad de que al acercarse x a p, entonces f(x) se acerca a L, se escribe: Ejemplos: Gráficamente: El límite L puede no coincidir con f(p), f(p) ≠ L, o incluso no estar definido f(p) por no pertenecer p al dominio de definición de la función f. Para hablar de límite es preciso que f esté definida en un entorno “perforado” de p. Ejemplos: Una función típica en análisis es : Esta función no está definida en el punto x=1 . Para este valor de x, el denominador de la función es 0 , y no tiene sentido en matemáticas dividir por 0. El valor al que esta función se aproxima, cuando x tiende a 1 por la izquierda o por la derecha, es 2. Luego la función tiene límite cuando x se aproxima a 1 ; el límite es 2. Escribimos: Límites laterales: El límite de una función en un punto existe si y sólo si existen los límites laterales y son iguales. 1 El límite lateral por la izquierda de una función y=f(x) en el punto x = a es el valor al que se aproxima f(x) cuando x se aproxima al valor de a por valores menores que a. El límite lateral por la derecha de una función y = f(x) en el punto x = a es el valor al que se aproxima f(x) cuando x se aproxima al valor de a por valores mayores que a, Se representan por: Ejemplo: Sea la función f(x) en el punto x=2 no existe el límite, ya que ambos límites laterales no coinciden: Ejemplos: f(x)= x-[x] , la variable menos su parte entera, f(5.46)=5.46-5=0.46; f(10.25)=10.25-10=0.25, luego lim f(x)=1 pero lim f(x)=0, hacer el gráfico. 2 Propiedades de los límites Límite de una función en el infinito: Cuando x se hace tan grande o tan pequeña como se quiera, tanto los valores de x como los de la función f(x) pueden ser finitos o infinitos. Ejemplo : Analizar la función cuando x tiende a +∞ ó -∞, también cuando x tiende a 1: Ejemplos : Analizar el comportamiento de las funciones 1/x2 y 1/x en el punto x=0, que es una asíntota vertical en ambos casos. 3 Indeterminaciones: Hay varios tipos: , , , , , , Ejemplo: 0/0 es una indeterminación pues límites de cocientes donde los límites de dividendo y divisor separadamente son cero, pueden terminar dando cualquier cosa, como los siguientes: Si los límites no los obtenemos directamente al sustituir, hay que analizar cada caso para evitar las indeterminaciones, para las funciones racionales con polinomios descomponemos en factores y simplificamos, con raíces multiplicamos y dividimos por el conjugado de la raíz, en general: 1. Cuando el grado del numerador es mayor que el grado del denominador el resultado nos da +∞ ó -∞. 2. Cuando ambos tienen el mismo grado, la solución es el cociente de los coeficientes del mismo grado. 3. Cuando el grado del numerador es menor que el grado del denominador, la solución es 0. 4. Indeterminación 1∞ son funciones del tipo potencial-exponencial Ejemplos 4 Continuidad de una función: Una función es continua en el punto si Si una función es continua en el punto implica que y ambos existen y son iguales. Los valores que toma la función f(x) en puntos próximos a x0 deben estar próximos a f(x0), lo cual implica que la gráfica no salta bruscamente en x=x0, ni toma valores sensiblemente espaciados cuando x se aproxima suficientemente a x0. Una función es continua en un intervalo si es continua en todos los puntos del intervalo. Una función es continua en todo su dominio cuando lo es en todos los puntos que lo componen. Discontinuidades: Una función es discontinua en un punto dicho punto. si no es continua en Tipos de discontinuidades Discontinuidad evitable: Una función tiene una discontinuidad evitable en un punto cuando existe el límite de la función en dicho punto. Ejemplo La función f(x) definida por: no es continua en el punto Como porque mientras que existe, la discontinuidad que tiene en el punto , es decir: es evitable. Una función presenta una discontinuidad de primera especie o inevitable de salto finito en el punto si los limites laterales de en existen (son finitos) pero son distintos, es decir: 5 Ejemplo: La función f(x) definida por: no es continua en el punto distintos: porque no existe, al ser ambos límites laterales Como ambos límites laterales existen, la discontinuidad que tiene la función es de primera especie. en el punto Una función presenta una discontinuidad de segunda especie o inevitable de salto infinito en el punto si no existe alguno de los límites laterales de en dicho punto. Ejemplo: La función definida por: no es continua en el punto izquierda de cuando especie: , porque tiene en el punto no existe, al no existir el límite por la una discontinuidad de segunda Ejemplo: Calcular los valores de a y de b para que la siguiente función sea continua: Continuidad en x = 0, calcular los límites laterales en x = 0 Continuidad en x = 1, calcular los límites laterales en x = 1 Si a = 3 y b = -1 la función es continua para todos los números reales. Aparte de los libros de Matemáticas aplicadas a las Ciencias Sociales de 2º año de Bachillerato, se recomiendan las siguientes páginas sobre estos temas para estudiar y resolver problemas: http://matematicasies.com www.vadenumeros.es http://www.matematicasbachiller.com 6 Asíntotas Las asíntotas son rectas a las cuales la función se va aproximando indefinidamente, cuando por lo menos una de las variables (x o y) tienden al infinito. Son límites de las funciones. Asíntotas Verticales: Nos indican a que tiende la función cuando la x no está definida, son rectas paralelas al eje OY. Se escriben x = valor de la asíntota horizontal. El número máximo de asíntotas verticales que puede tener una función es dos. Asíntotas Horizontales: Nos indican a que tiende la función cuando la x es muy grande o muy pequeña, son rectas paralelas al eje OX. Se escriben y = valor de la asíntota horizontal. Las funciones racionales tienen asíntota horizontal cuando el numerador y el denominador son del mismo grado y cuando el grado del denominador es mayor que el grado del numerado. Asíntotas oblicuas: una función racional tiene asíntotas oblicuas cuando el grado del numerador es una unidad mayor que el grado del denominador. Las asíntotas horizontales y oblicuas son incompatibles. Si hay unas no puede haber de las otras. Función : Es una relación entre los elementos de dos conjuntos, de forma que a determinados elementos del primer conjunto se asocian elementos del segundo conjunto de manera unívoca, es decir que a un elemento del primer conjunto no le podemos asociar más de un elemento del segundo conjunto. A un elemento cualquiera del primer conjunto lo representamos con la letra x, que denominamos variable independiente y al único elemento que le corresponde en el segundo conjunto lo representamos por la letra y, a la que denominamos variable dependiente. A la relación la representamos por la letra f y escribimos y=f(x). Dominio de definición de una función f : Es el conjunto de valores de x para los que la función f(x) existe. Lo representamos por Dom(f). Recorrido o imagen de una función f : Es el conjunto de valores que toma la variable dependiente y. Lo representamos por Img(f). Según la expresión analítica clasificamos las funciones de variable real, de la siguiente forma: 7