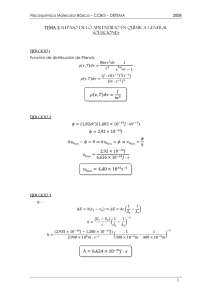
Tema 8: Métodos aproximados Soluciones

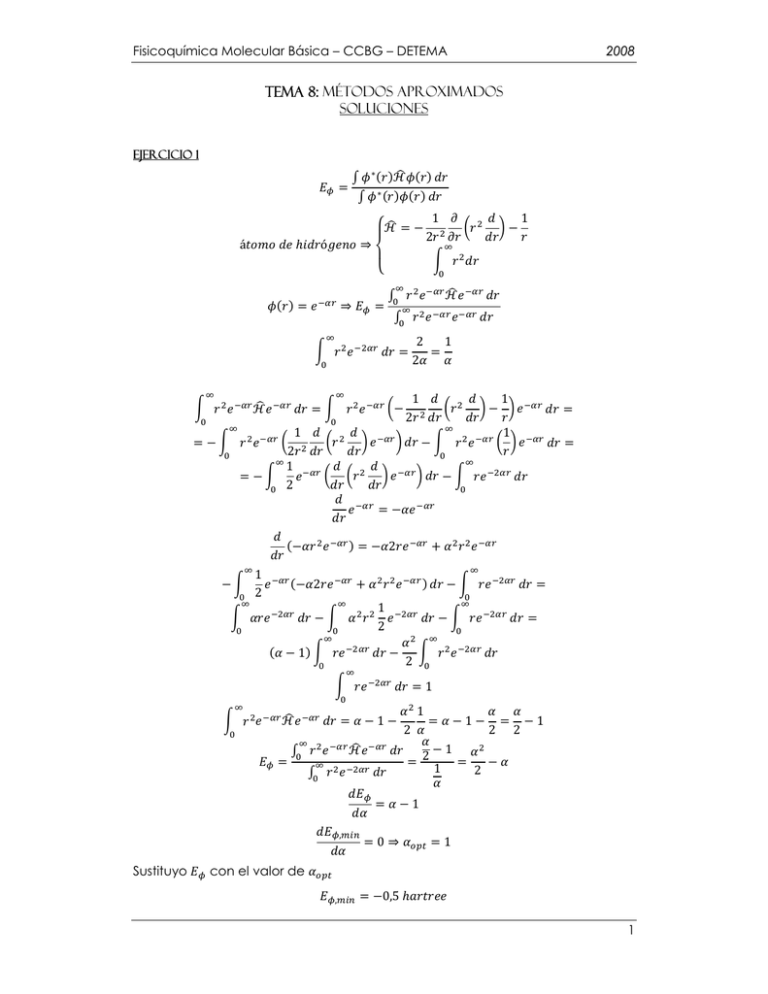
Fisicoquímica Molecular Básica – CCBG – DETEMA
2008
Tema 8: Métodos aproximados
Soluciones
Ejercicio 1
á
1
1
2
ó
2
2
1
1
2
1
2
1
2
1
1
2
1
2
2
1
2
1
2
1
1
1
1
2
2
2
2
1
1
1
2
1
,
Sustituyo
0
1
con el valor de
,
0,5
1
Fisicoquímica Molecular Básica – CCBG – DETEMA
2008
Ejercicio 2
2
ó
2
1
2
2
1
1
1
1
1
2
1
2
1
1
2
1
1
1
1
1
C.V.
.
·
·
Los límites de integración se mantienen inalterados.
1
1
1
1
2
1
1
1
1
4
1
1
1
2
1
2
1
1
2
1
1
1
2
1
1
1
2
1
2
1
4
1
1
2
4
1
1
4
1
·
4
1
1
C.V.
1
1
2
1
1
1
1
4
1
1
1
1
1
2
1
1
1
1
1
2
1
1
.
2
Fisicoquímica Molecular Básica – CCBG – DETEMA
2008
·
1
1 1
4
1
1 1 1
2
1
1
1
∞
1
2
1
1
1
1 4
1
32
1 1
2
2
1
1
1 1
2
1
1
1
2
3
16
1
1
3
8
4
32
1
1
1
1
4
4
4
1
1
8
1
1
4
2
4
1
4
1
1
8
1
1
1
1
2
,
Sustituyo
1
1
8
4
1
8
1
32
1
4
2
3
16
1
2
1
1
1
3
16
1
1
1
1
4
0
1
2
1
2
1 1
2
1
√2
con el valor de
1
,
4√2
3
Fisicoquímica Molecular Básica – CCBG – DETEMA
2008
Ejercicio 3
1:
1
·
√
1
2
√
1
·
1
2
1
1
2
1
2
4
Ejercicio 4
a)
2
í
2
2
2
2
.
2
2
2
4
6
2
2
2
12
12
20
4
Fisicoquímica Molecular Básica – CCBG – DETEMA
12
2
12
12
2
24
2
2
2
12
12
5
20
.
2
14
14
3
2
.
|
.
2
2
2
90
14
3
.
.
12
12
5
|
6
2
12
.
24
4
12
12
12
2
2008
.
|
36
70
2
15
15
30
2
.
2
2
2
2
2
2 .
2
2
2
2 .
2
.
.
1
5
6
2
1
2
15
30
.
|
.
2
3
|
1
5
1
2
2
3
10
5
Fisicoquímica Molecular Básica – CCBG – DETEMA
2008
30
b)
2
2
.
2
.
.
3
2 .
2
1
2
.
1
3
2
6
6
2
2
2
2
12
2
12
36
12
2
36
.
2
12
7
38
2
16
.
2
.
.
.
16
38
5
6
630
.
2
.
2
.
2
3
4
798
105
2
.
12
12
38
180
.
2
420
70
105
.
.
.
2
.
.
5
2
3
30
6
Fisicoquímica Molecular Básica – CCBG – DETEMA
.
4
.
6
9
2
4
.
.
2
.
4
.
6
7
2
2008
6
4
6
.
4
70
.
315
.
540
630
5
420
126
630
.
.
2
20
.
3
3
70
84
.
7
2
3
5
4
35
140
140
c) Determinante Secular:
0
6
30
30
140
30
140
105
630
0
Teorema sobre determinantes: La multiplicación de todos los elementos de
cualquier fila (o columna) por alguna constante k, multiplica el valor del
determinante por k.
7
Fisicoquímica Molecular Básica – CCBG – DETEMA
2008
Usando ese teorema, se eliminan las fracciones multiplicando la fila 1 del
determinante por 420 ⁄ , la fila 2 por 1260 ⁄ , y el lado derecho del
determinante por ambos factores. Así se obtiene:
14
9
70
42
14
12
3
2
56
⁄
√532
28
0
252
0.1250018
⁄
0
, 1.293495
Como lo que se pide es la energía del estado basal:
⁄
0.1250018
⁄
d) Volviendo al planteo matricial original:
0
El sistema de ecuaciones queda, entonces:
0
0
Así, sustituyendo por el valor de E obtenido en el paso anterior:
70
14
42
12
14
70
3
14
9
42
2
12
14
4
4
4
0.1250018
0.023095
3
0.1250018
0.020381
9
0.1250018
0.061144
4
Dividiendo todos los términos por
2
0.1250018
0.053960
, el sistema de ecuaciones queda,
entonces:
0.023095
0.061144
0.020381
0.053960
0
0
8
Fisicoquímica Molecular Básica – CCBG – DETEMA
2008
(Cabe aclarar que el superíndice (1) indica que son los coeficientes obtenidos
para el nivel de energía basal).
Lo que se tiene es un sistema de ecuaciones lineales homogéneas, para el
cual se ha demostrado que tiene una solución no trivial si y sólo si el
determinante de los coeficientes es cero (cosa que se cumple en nuestro
ejemplo). La solución de este sistema contiene una constante arbitraria, y no
se puede determinar un valor único para cada incógnita. Así, para resolver el
sistema, se asigna un valor arbitrario a una cualquiera de las incógnitas, por
, se pasa el último término de cada ecuación al lado derecho del
ejemplo,
igual y se despeja la razón entre los coeficientes. Se obtiene así:
1.133 ⁄
,
Ahora se puede calcular k considerando la condición de normalización:
|
1
1.133
⁄ |
|
2.266
2.266
⁄
1.133
|
⁄
⁄
1.284
⁄
1.284
|
⁄
0.05156
1
Así:
4.404⁄
⁄
y, por tanto,
4.404⁄
⁄
4.990 ⁄
,
⁄
Ejercicio 5
Partícula de masa m, en una caja situada entre 0
El sistema conocido es la partícula en la caja, entonces:
2
2
2
y la perturbación en este caso es:
Para
,
. sin
9
Fisicoquímica Molecular Básica – CCBG – DETEMA
2
.
2
. sin2
2
cos
2
cos 2
sin 2
4
4
. sin
.
2
8
2
2
2
. sin
.
sin
4
2008
cos 0
8
0
1
1
8
2
8
2
10