ejersiselem42
Anuncio
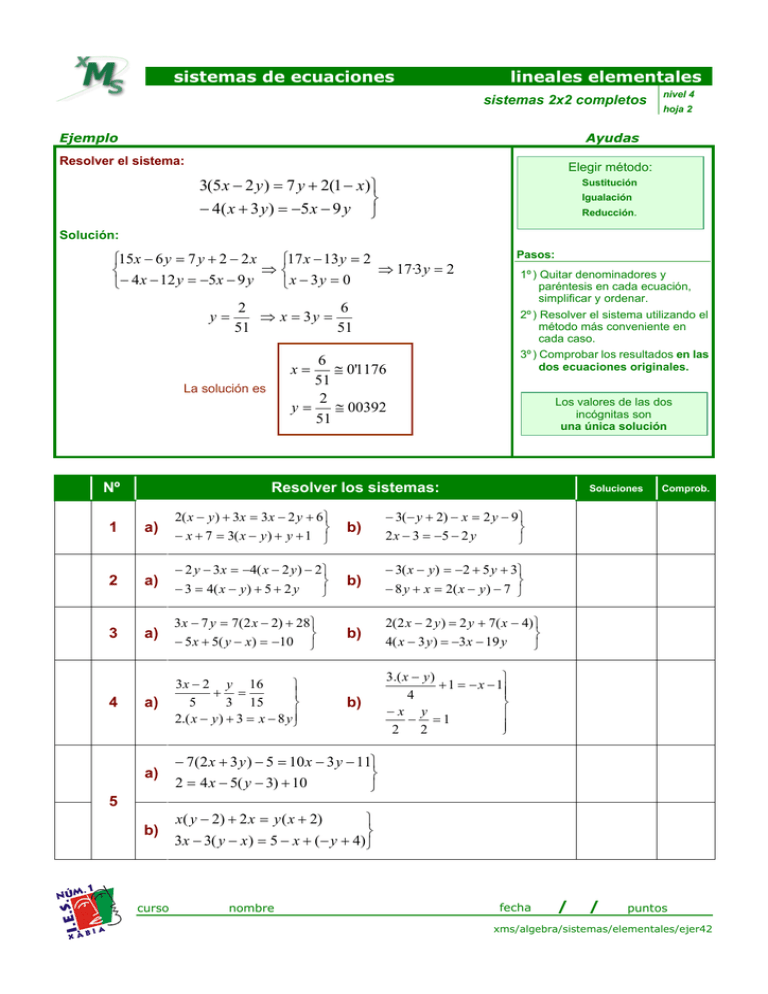
sistemas de ecuaciones lineales elementales sistemas 2x2 completos Ejemplo nivel 4 hoja 2 Ayudas Resolver el sistema: Elegir método: 3(5 x − 2 y ) = 7 y + 2(1 − x) − 4( x + 3 y) = −5 x − 9 y Sustitución Igualación Reducción. Solución: 15x − 6 y = 7 y + 2 − 2 x 17 x − 13 y = 2 ⇒ ⇒ 17·3 y = 2 − x − y = − x − y x y − = 4 12 5 9 3 0 y= Pasos: 1º ) Quitar denominadores y paréntesis en cada ecuación, simplificar y ordenar. 2º ) Resolver el sistema utilizando el método más conveniente en cada caso. 3º ) Comprobar los resultados en las dos ecuaciones originales. 2 6 ⇒ x = 3y = 51 51 6 ≅ 0'1176 51 2 y= ≅ 00392 51 x= La solución es Nº Los valores de las dos incógnitas son una única solución Resolver los sistemas: Soluciones 1 a) 2( x − y ) + 3x = 3 x − 2 y + 6 − x + 7 = 3( x − y ) + y + 1 b) − 3(− y + 2) − x = 2 y − 9 2 x − 3 = −5 − 2 y 2 a) − 2 y − 3 x = −4( x − 2 y ) − 2 − 3 = 4( x − y ) + 5 + 2 y b) − 3( x − y) = −2 + 5 y + 3 − 8 y + x = 2( x − y ) − 7 3 a) 3 x − 7 y = 7(2 x − 2) + 28 − 5 x + 5( y − x) = −10 b) 2(2 x − 2 y ) = 2 y + 7( x − 4) 4( x − 3 y ) = −3 x − 19 y a) 3 x − 2 y 16 + = 5 3 15 2.( x − y ) + 3 = x − 8 y b) 3.( x − y ) + 1 = − x − 1 4 −x y − =1 2 2 a) − 7(2 x + 3 y ) − 5 = 10 x − 3 y − 11 2 = 4 x − 5( y − 3) + 10 b) x( y − 2) + 2 x = y ( x + 2) 3x − 3( y − x ) = 5 − x + (− y + 4) 4 Comprob. 5 curso nombre fecha / / puntos xms/algebra/sistemas/elementales/ejer42