Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
I NTRODUCCIÓN AL A NÁLISIS M ATEMÁTICO
N ÚMEROS REALES -P LANO
CARTESIANO -V ECTORES EN EL PLANO
Ciencias Básicas y Tecnológicas
IAM
Trujillo
E.G.U.N.T.
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Contenido
1
Competencia/ Capacidad
2
Motivación
3
Números reales
Conjuntos numéricos
Sistema de números reales
4
Sistema Unidimensional
5
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Competencia/Capacidades
Competencia
Formula y aplica conocimientos matemáticos para obtener y
dar solución a problemas científicos y tecnológicos,
propiciando el desarrollo de la ciencia y contribuyendo a la
mejora de su entorno. Asímismo, transmite y difunde el
conocimiento matemático y su utilidad, a través de la
investigación, con responsabilidad y ética.
Capacidad Terminal
Propone soluciones imaginativas viables y eficaces a
problemas académicos y de la comunidad para fortalecer el
pensamiento crítico, la cultura investigativa y la innovación.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Problema
Problema: de números reales
Una vendedora gana un salario base de 1600 soles mensuales
más una comisión del 10 % de las ventas que haga. Descubre
que en promedio, le toma 1 12 horas realizar ventas por un valor
de 200 soles. ¿Cuántas horas deberá trabajar en promedio
cada mes para que sus ingresos sean de 6000 soles?
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Problema
Problema: de números racionales
Si a, b, c, y d son números reales, con b y d no nulos, se tiene
que
a
c
ad + cb
+ =
b d
bd
¿Cómo se demuestra esta igualdad de los números reales?
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Problema
Problema: Longitud de una cuerda
Un Ingeniero utiliza una cuerda cuya tercer cuarta parte mide
90 metros. ¿Cuanto mide la cuerda?.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Problema
Problema: Dimensiones
Un ingeniero debe cercar un terreno de forma rectangular, que
tiene dos de sus vértices en los puntos (2,5) y (8,-2). ¿Qúe
dimensiones tiene el terreno?. Si las paredes deben tener
2mts. de alto, ¿que área total tiene el cerco, suponiendo que
no tiene puerta?
Figura: Cerco
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Conjuntos numéricos
Sistema de números reales
Conjuntos Numéricos
Figura: Conjuntos numéricos
Figura: Recta real
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Conjuntos numéricos
Sistema de números reales
Sistema de los números reales
Definición axiomática
Se llama sistema de números reales al conjunto no vacío de
los números reales,R, y dos operaciones internas: adición y
multiplicación, denotadas por + y · donde
+ : R × R → R : (a, b) → a + b y · : R × R → R : (a, b) → a · b, y
una relación de orden > que satisfacen los siguientes axiomas:
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Conjuntos numéricos
Sistema de números reales
Definición axiomática
1.-Axiomas de adición y multiplicación
a+b ∈R
a+b =b+a
∀ a, b ∈ R
(a + b) + c = a + (b + c)
∃!0 ∈ R : a + 0 = 0 + a = a
∃! − a ∈ R, ∀ a ∈ R : (−a) + a = a + (−a) = 0
a·b ∈R
a·b =b·a
∀ a, b ∈ R
(a · b) · c = a · (b · c)
∃!1 ∈ R : a · 1 = 1 · a = a
∀ a ∈ R \ 0, ∃! a1 ∈ R, : (a) a1 = a1 (a) = 1
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Conjuntos numéricos
Sistema de números reales
Definición axiomática
2.-Axiomas de Distributividad
a · (b + c) = a · b + a · c
(b + c) · a = ba + ca
3.-Axiomas de Igualdad
a = b o a ̸= b.
a = a.
a = b → b = a.
a = b ∧ b = c → a = c.
Si a = b → a + c = b + c.
Si a = b → ac = bc.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Conjuntos numéricos
Sistema de números reales
Definición axiomática
4.-Axiomas de orden
Solo una se cumple: a < b ó a = b ó a > b.
Si a < b y b < c → a < c.
Si a < b → a + c < b + c ∀ c ∈ R
Si a < b y c > 0 → ac < bc.
Si a < b y c < 0 → ac > bc.
Existe R+ tal que R+ ⊂ R llamado conjunto de los reales
positivos tal que:
0∈
/ R+ .
Si a y b ∈ R+ → (a + b) ∈ R+ .
Para cada a ̸= 0 : a ∈ R+ ó −a ∈ R+ (no ambos).
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Conjuntos numéricos
Sistema de números reales
Definición axiomática
5.-Axioma del supremo
Todo subconjunto no vacío A de R, acotado superiormente,
tiene una menor cota superior, llamada EL SUPREMO de A.
Este axioma nos garantiza la inclusión de los números
racionales, Q en el conjunto de los números reales y que se
puede establecer una correspondencia biunívoca entre los
puntos de una recta con los números reales
Todos estos axiomas permiten demostrar las propiedades
algebraicas de las operaciones en los números reales
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Conjuntos numéricos
Sistema de números reales
Ejemplo
1.- Use los axiomas y demuestre que a · 0 = 0 para a ∈ R
Solución
a·0 = a·0+0
(ax. − 1,4)
= a · 0 + [a · 0 + (−a · 0)]
(ax. − 1,5)
= (a · 0 + a · 0) + (−a · 0)
(ax. − 1,3)
= a · (0 + 0) + (−a · 0)
= a · 0 + (−a · 0)
= 0
(ax. − 1,4)
(ax. − 1,5)
E.G.U.N.T.
(ax. − 2,1)
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Conjuntos numéricos
Sistema de números reales
Ejemplo
2.- Demuestre que para todo a ∈ R; −(−a) = a
Solución
Sea b = (−a) como b ∈ R, entonces b + a = (−a) + a = 0 por
el axioma de existencia y unicidad del elemento neutro aditivo;
entonces para cada b ∈ R, existe un único elemento −b tal
que b + (−b) = 0, entonces a = (−b), por lo tanto a = −(−a).
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Eje Numérico
Eje numérico
Sea X ′ X una recta con dirección positiva de izquierda a
derecha, el punto fijo O ubicado al centro de la recta se llama
origen. Si A es un punto a una unidad a la derecha de O,
entonces el punto P1 contiene x1 veces la unidad OA, x1 es un
número real positivo llamado coordenada de P1 .
Analogamente, si P2 es un punto cualquiera de la recta X ′ X
ubicado a la izquierda de O, se le hace corresponder el
número real negativo x2 .
Figura: Sistema unidimensional
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Consideraciones a tener en cuenta
Observaciones
Cualquier número real x puede representarse por un
punto P sobre la recta X ′ X y reciprocamente cualquier
punto P sobre la recta X ′ X representa a un número real x.
El valor númerico de x es igual a la longitud del segmento
¯ y cuyo signo es positivo o negativo según P se ubique
OP
a la derecha o izquierda de O respectivamente.
Esta correspondencia biunívoca entre los puntos de una
recta y los números reales se llama sistema coordenado
unidimensional.
Notación del punto P con su coordenada x: P(x).
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia dirigida en la recta
Distancia dirigida
La distancia del punto A(x1 ) al punto B(x2 ) es:
d(A, B) = x2 − x1
Observaciones
Si x2 > x1 (A se encuentra a la izquierda de B), entonces
d(A, B) > 0
Si x2 < x1 (A se encuentra a la derecha de B), entonces
d(A, B) < 0.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Ejemplos
1
En una recta L se ubican de manera consecutiva A, C, D y
B; de tal manera que el punto D es punto medio del
¯ AC
¯
¯ = CB−
¯ Muestre que CD
segmento AB.
.
2
2
En una recta se ubican consecutivamente los puntos
A, B, C y D. Sea M el punto medio del segmento AB y sea
N el punto medio del segmento CD; si el segmento
AC = 18 y el segmento BD = 4, cual es la longitud del
segmento MN?.
3
Sobre una recta L se ubican los puntos A, B, C, E tal que
AB = BC, CE = 2AC y AD = 12 (AE). Muestre que
AD = AB + AC.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia No dirigida
Distancia No dirigida
La distancia no dirigida entre los puntos A(x1 ) y B(x2 ) es:
d = |x2 − x1 | = |x1 − x2 |
Observaciones
El valor absoluto se usa porque no importa que
coordenada es mayor.
Si L es una recta orientada, existe una función
d : L × L → R llamada distancia tal que d(A, B) ≥ 0;
d(A, B) = 0 ⇔ A = B; d(A, B) = d(B, A) ∀, A, B ∈ R y
d(A, C) ≤ d(A, B) + d(B, C) ∀, A, B, C ∈ R.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Ejemplos
Determine los puntos en la recta cuyas coordenadas
satisfacen las siguientes ecuaciones: a)|x − 2| = 5;
b)|2x − 10| = 5 − x; c)|x − 3| + |x + 1| = 8.
Si a < b ubique los números dados en la recta real y dar la
7a+b
relación de orden que cumplen: a) a+3b
4 . b) 8 .
Dados los puntos M(−2) y N(8). Halle los puntos P y Q
¯
que trisecan al segmento MN.
Si la distancia no dirigida entre los puntos A y B es 8 y si A
tiene coordenada (−4). Cual es la coordenada de B?.
Interprete geometricamente su respuesta.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Sistema coordenado rectangular
Sistema coordenado rectángular
Formado por pares ordenados de números reales que resultan
de la intersección de dos rectas ortogonales entre si y de todas
las combinaciones posibles de sus elementos, generando así
el conocido plano cartesiano, denotado por R2 ; es decir:
R2 = {(x, y ) : x ∈ R; y ∈ R}
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Elementos del sistema coordenado rectangular
Elementos del sistema coordenado rectangular
Figura: Elementos del plano cartesiano
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
observaciones
Cada par ordenado (x, y ) en el plano, se puede asociar de
manera única con un punto P.
El par (x, y ) son las coordenadas del punto P y se llaman:
abscisa y ordenada respectivamente.
Las abscisas se ubican en la recta horizontal y las
ordenadas en la vertical.
Las rectas ortogonales entre si, se llaman ejes de
coordenadas.
El punto de intersección de los ejes de coordenadas, se
llama origen del sistema y se denota con O.
P(x, y ) denota al punto P con sus coordenadas (x, y ); su
representación gráfica resulta de la intersección de rectas
paralelas a los ejes de coordenadas.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Distancia entre dos puntos
Definición
Sean P1 (x1 , y1 ) y P2 (x2 , y2 ), puntos en R2 , se define la
distancia entre ellos, como:
q
d(P1 , P2 ) = (x2 − x1 )2 + (y2 − y1 )2
Distancia entre dos puntos
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Propiedades de la distancia
Propiedades
d(P1 , P2 ) ≥ 0 ∀ P1 , P2 ∈ R2
d(P1 , P2 ) = d(P2 , P1 )
d(P1 , P2 ) = 0 ⇔ P1 = P2 .
Para cualquier P3 ; d(P1 , P2 ) ≤ d(P1 , P3 ) + d(P3 , P2 )
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Ejemplos
1
Halle las coordenadas del punto que equidista de los
puntos fijos A(4, 3), B(2, 7) y C(−3, −8).
2
Muestre que el triángulo de vértices A(4, 7), B(−1, −8) y
C(8, −5) es un triángulo rectángulo. Halle su perímetro y
su área.
3
La abscisa√de un punto es -3 y su distancia al punto
A(2, 3) es 50. Hallar la ordenada del punto.
4
Dos vértices de un triángulo equilátero son A(3, 1) y
B(−1, −1). ¿Cuáles son las coordenadas del tercer
vértice?
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Vectores en el plano
Definición algebraica
Es un par ordenado de números reales (x, y ) llamados
componentes del vector, denotado por:
x
u=
y
El vector cero es el vector (0, 0)
Definición geométrica
El conjunto de todos los segementos de recta dirigidos
equivalentes a un segmento de recta dirigido dado se llama
vector. Cualquier segmento de recta de este conjunto es el
representante del vector.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Representación de un vector
Figura: Vector en el plano
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Vectores en el plano
Elementos
1
2
x
Modulo: Es la longitud de un vector, si u = 1 , el
y1
módulo de u es:
q
∥u∥ = x12 + y12
Dirección: Es la dirección de la recta que contiene al
vector. Es el ángulo θ medido en radianes que forma el
vector u = (x, y ) con el lado positivo del eje X . Con
0 ≤ θ ≤ 2π. Si x ̸= 0
tagθ =
E.G.U.N.T.
IAM
y
x
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Vectores en el plano
Observaciones
Si dos vectores son paralelos tienen la misma dirección.
Sentido: Es el que va del origen al extremo, se representa
con una flecha. Una dirección tiene 2 sentidos.
Un vector que inicia en el punto P1 y finaliza en el punto
P2 , se dice que es un vector localizado en el plano. Su
−−−→
notación es: P1 P2 .
−−−→
El vector localizado P1 P2 es equivalente al vector de
posición u = P2 − P1
Para determinar la dirección de un vector de manera única
es necesario conocer el cuadrante donde se ubica el
vector.(Si x ̸= 0 siempre existen dos números en [0, 2π]
tales que tanθ = yx ; esto se debe al periodo 2π de tanθ.)
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Traslación de vectores
Figura: Traslación de vectores
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Ejemplos
1
2
3
4
5
Determine las longitudes
√ y dirección de los vectores
u1 = (2, 2); u2 = (−2 3, 2); u3 = (−3, −3); u4 = (6, −6) y
u5 = (0, 3)
−−−→
Halle el vector de posición de P1 P2 si P1 (5, −2) y P2 (2, 3).
Interprete geometricamente su resultado.
Un vector que va de A(3, 5) a D(x, y ) representa al mismo
vector que va de D(x, y ) a B(8, 1). Halle D(x, y ).
−→
Si P(6, −1) y Q(−2, 5) son el inicio y final del vector PQ.
Determine la longitud del vector PQ.
Los vértices de un triángulo son (3,3), (-1,-2) y (4,1).
Determine el área de dicho triángulo.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Operaciones con vectores
Sean u = (x1 , y1 ), v = (x2 , y2 ) y w = (x3 , y3 ), vectores en el
plano y r un escalar, entonces se cumple:
1
Igualdad de vectores: u = v ⇔ x1 = x2 y y1 = y2 .
2
Suma de vectores:El vector suma de u y v es:
u + v = (x1 + x2 , y1 + y2 ).
3
Producto de un vector por un escalar: El vector que se
obtiene de efectuar el producto de un escalar, r , por un
vector es:
ru = (rx1 , ry1 ).
Si r > 0, el vector ru tiene la misma dirección que el vector
u, mientras que si r < 0, ru tiene dirección opuesta al
verctor u.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Observaciones
|u + v | ≤ |u| + |v |, llamada desigualdad triangular.
En R2 los vectores i = (1, 0) y j = (0, 1) permiten
representar a cualquier vector en R2 , es decir:
u = (x, y ) = xi + yj
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Ejemplos
1
Dados los siguientes vectores, realice las operaciones
indicadas: u = (−2, −7), v = (1, 4), w = (3, −4),
t = (−5, 7).
a) 2u + t; b)2w + u. c) 3v + (−3)t; d)−2t + 5u.
2
Determine el vector u, si se cumple 3(−2, 3) + 2u = (6, 4).
3
Determine todos los números reales r y s talque:
r (4, −6) + s(5, 6) = (6, 18).
4
Sean u = (−2, 3) y v = 4, −3. Un segmento dirigido que
representa al vector ( 23 u − 16 v ) tiene un punto inicial en
w = (5, 3/2). Determine el punto final.
5
Determine un vector unitario que tenga la misma dirección
que el vector v = 2i − 3j.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Producto escalar de vectores
Producto escalar de vectores
Sean u = (x1 , y1 ) y v = (x2 , y2 ), el producto escalar o interno
de u y v , denotado por u · v , se define por;
u · v = x1 x2 + y1 y2
Observaciones
Es una operación cuyo resultado no es un vector sino un
número real o escalar.
Magnitud de un vector en términos del proucto escalar:
∥u∥2 = u · u.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Interpretación Geométrica del producto escalar
Interpretación Geométrica
El producto escalar de 2 vectore no nulos de R2 es la magnitud
o norma del vector proyección de uno de ellos sobre el otro
vector multiplicado por un escalar
Figura: Producto escalar
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Interpretación del producto escalar
Sean u y v dos vectores y sea u − v el vector que une los
extremos finales de los vectores u y v , los cuales forman un
triángulo rectángulo siempre que u y v sean ortogonales.
Entonces por el teorema de pitagoras se tiene:
∥u − v ∥2 = (∥u∥)2 + (∥v ∥)2
Propiedades
El vector u es ortogonal al vector v si y sólo si u · v = 0.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Angulo entre dos vectores
Definición
Sean u y v dos vectores diferentes de cero. Entonces el ángulo
θ entre ellos está definido como el ángulo no negativo más
pequeño(entre [0, π])entre las representaciones de u y v que
tiene al origen como inicio. Si u = rv para r escalar, entonces
θ = 0 si r > 0 y θ = π si r < 0.
Angulo entre dos vectores
Sean u = (x1 , y1 ) y v = (x2 , y2 ), dos vectores distintos de cero.
Si 0 ≤ θ ≤ π es el ángulo entre u y v es:
cos(θ) =
u·v
∥u∥∥v ∥
E.G.U.N.T.
(0 ≤ θ ≤ π)
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Otra forma de definir al producto escalar
u · v = ∥u∥∥v ∥cosθ
Figura: Angulo entre vectores
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Definiciones
Vectores Paralelos: u y v diferentes de cero son
paralelos si θ es 0 o pi, es decir
u = rv r ∈ R.
Vectores ortogonales: u y v diferentes de cero son
ortogonales o perpendiculares si:
u · v = 0.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Propiedades
Propiedades
Sean u, v y w vectores en el plano:
|u · v | ≤ ∥u∥∥v ∥ (desigualdad de Cauchy Schwartz).
|u · v | = ∥u∥ + ∥v ∥ si y sólo si u es paralelo a v .
√
∥u∥ = u · u.
u · v = v · u.
u · u > 0, si u > 0 pero u · u = 0, si y solo si u = 0.
(u + v ) · w = u · w + v · w.
(ru) · v = u · (rv ) = r (u · v ).
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Definiciones
Vector unitario
Un vector u tal que ∥u∥ = 1 se llama vector unitario.
u
Si u ̸= 0 el vector ∥u∥
es un vector unitario en la dirección de u.
dirección
Dos vectores u y v tienen la misma dirección si y sólo si u = rv
para r escalar mayor que cero; y tienen direcciones opuestas
para algún escalar r negativo.
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Ejemplos
1
Dados los siguientes vectores, halle el producto escalar
u · v ; el ángulo entre ellos: u = (−2, 7), v = (1, 4).
2
Determine el vector u, tal que sea ortogonal al vector
w = (−3, 4).
3
Si A = (−8, 6), B = (−3, 4) y C = (−1, 9), usando
métodos vectoriales demuestre que el triángulo △ ABC es
un triángulo rectángulo.
4
Halle un vector unitario que siga la direccion de
w = (−3, 6).
5
Halle el ángulo entre los vectores u = (3, −2) y v = (7, 2)
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
Proyección de vectores
Proyección ortogonal
Sean u y v y diferentes de cero, la proyección vectorial de u
sobre v es:
u·v
v
proyv (u) =
v ·v
Obervaciones
La componente de u en la dirección de v es el escalar u·v
|v | .
El vector w = u − vu·v
·v v es perpendicular a v y se llama
proyección ortogonal de u sobre v .
E.G.U.N.T.
IAM
Competencia/ Capacidad
Motivación
Números reales
Sistema Unidimensional
Sistema bidimensional
Distancia entre dos puntos
Vectores en el plano
Operaciones con vectores
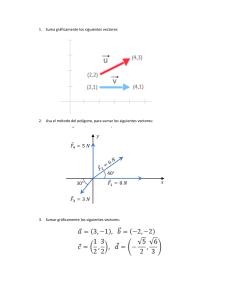
Ejercicios
1
Determine el producto escalar y el coseno del ángulo entre
los vectores:
1
2
3
u = (7, 9) y v = (−8, 9).
(3, −8) y (−5, 1).
(3, 0) y (0, −7)
2
Sean u = 2i − 3j y v = i + j. Determine proyv (u).
3
Muestre que para cualquier numeros reales α y β, los
vectores u = αi + βj y v = βi − αj son ortogonales.
4
Si u = −3i + 6j y v = 2i + αj. Determine un α tal que el
ángulo entre ellos sea π/4.
E.G.U.N.T.
IAM