funciones

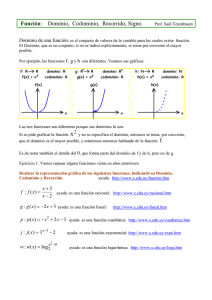
FUNCIONES
FUNCIÓN

Definición:
 Sean A y B conjuntos no vacíos. Una función de A en B es una
relación que asigna a cada elemento x del conjunto A uno y
solo un elemento y del conjunto B.
Se expresa como:
f: A
x
B
f(x) = y
Se dice que y es la imagen de x mediante f, y que x es la
pre-imagen de f(x) = y
FUNCIÓN

Conceptos:
Dominio: es el conjunto de todos los valores para los cuales
está definida la función y se denota Dom f.
 Rango : es el conjunto de todos los valores que toma la
variable dependiente (Y), y se denota Ran f.
 Función Creciente: es aquella que al aumentar la variable
independiente, también aumenta la variable
dependiente.
 Función Decreciente: es aquella que al aumentar la variable
independiente, la variable dependiente disminuye.

FUNCIÓN

Conceptos Fundamentales:

Si tenemos una relación f entre dos conjuntos A y B, f se dirá
función si a cada valor del conjunto de partida A le
corresponde uno y sólo un valor en el conjunto de llegada B.
A
f
B
a
b = f(a)
x
f(x)
f(x)
FUNCIÓN

Conceptos Fundamentales:

La variable x corresponde a la variable independiente y la
variable cuyo valor viene determinado por el que toma x, se
llama variable independiente. Se designa generalmente por y o
f(x) [se lee “f de x”]. Decir que “y” es función de “x” equivale a
decir que “y” depende de “x”.
A
f
B
a
b = f(a)
x
f(x)
FUNCIÓN
o
Conceptos Fundamentales
Se dirá:
 f:A
B
 b € B es la imagen de a € A bajo la función f y se denota por
b= f(a)
Dom f =A
 Si (x, y) € f ^ (x, z) € f

y = z (Unívoca)
Toda función es relación, pero no toda relación
es función.
FUNCIÓN

Rango o Recorrido de f:
Es aquel subconjunto del codominio en el cual todos sus
elementos son imagen de alguna preimagen del dominio o
conjunto de partida. Se denota por Rec f.
A
a
b
c
d
e
f
B
1
2
3
4
5
6
7
Se puede ver que para todo elemento de A, existe sólo una
imagen en B.

Luego para la función f denotada:
A
f
a
b
c
d
e



Dominio de f = Dom f
Codominio
Rango o Recorrido de f = Rec f
B
1
2
3
4
5
6
7
= A = {a, b, c, d, e}
= B = {1, 2, 3, 4, 5, 6, 7}
= {1, 2, 3, 4, 7}
Los elementos {5, 6} no son imagen de ninguna
preimagen en A, luego no pertenecen al rango de f .
CLASIFICACIÓN

a) Función Inyectiva: Una inyección de A en B es toda f de A en
B, de modo que a elementos distintos del dominio A le
corresponden imágenes distintas en el codominio B.
Cada elemento de A tiene una única imagen en B (y sólo una), de
tal forma que se verifica que # A ≤ # B.
f
A
a
b
c
d
1
2
3
4
5
B
Como se ve, 4 € B y no es imagen de ningún elemento de A

b) Función Epiyectiva o Sobreyectiva: Una epiyección o
sobreyección de A en B, de modo que todo elemento del codominio
B es imagen de, al meno, un elemento del dominio A. Cada
elemento de B es imagen de por lo menos un elemento de A. Se
verifica que # A ≥ # B. Es decir, que en este caso el codominio es
igual al recorrido.
f
A
a
b
c
d
B
1
2

c) Función Biyectiva: una función f es biyectiva de A en B si y
sólo si la función f es tanto Inyectiva como Epiyectiva a la vez, por
lo que se verifica que #A = #B y que a cada elemento de A le
corresponde una única imagen en B y que cada imagen de B le
corresponde una preimagen en A.
f
A
a
b
c
B
1
2
3
FUNCIÓN
La Respuesta correcta es B
FUNCIÓN
La Respuesta correcta es D
FUNCIÓN
La Respuesta correcta es E
I. FUNCIÓN LINEAL

Es de la forma f(x) = mx + n
con
m : Pendiente
n : Ordenada del punto de intersección entre la recta y el
eje Y (coeficiente de posición).
Ejemplo:
La función f(x) = 5x – 3, tiene pendiente 5 e intersecta al eje Y en
la ordenada -3.
I. FUNCIÓN LINEAL

Análisis de la Pendiente
Para saber con qué tipo de función se está trabajando, se debe
analizar el signo de la pendiente.
Si m < 0, entonces la función es decreciente.
• Si m = 0, entonces la función es constante.
• Si m > 0, entonces la función es creciente.
•
I. FUNCIÓN LINEAL
Y
Y
I)
II)
m>0
n>0
n
n
m<0
n>0
X
X
Y
Y
III)
IV)
m>0
n<0
m<0
n<0
X
n
X
n
I. FUNCIÓN LINEAL

Tipos de funciones especiales:

a) La función de forma f(x) = x, se reconoce como función
identidad y su gráfica es:
f(x)
2
1
-1
1
-1
2
x
I. FUNCIÓN LINEAL

Tipos de funciones especiales:

b) La función de la forma f(x) = c, con c: Constante Real, se
conoce como función constante y su gráfica es:
f(x)
f(x)
con c > 0
c
con c < 0
●
x
x
c
●
I. FUNCIÓN LINEAL

Propiedades:

El dominio de la función lineal son todos los números IR.

Las rectas que tienen la misma m serán paralelas.

Las rectas que al multiplicar sus pendientes el producto es -1
serán perpendiculares.
I. FUNCIÓN LINEAL

Evaluación de una función lineal:
Dada la función f(x) = mx + n, si se busca el valor de la función
para un valor cualquiera de x, basta reemplazar dicho valor, así
como también si se busca el valor de x conociendo el valor de la
función.
Ejemplo
La función que representa el valor a pagar en un taxi, después de
recorridos 200m es:
f(x) = 0.8x + 250
con
x: cantidad de metros recorridos
f(x): costo en pesos
3 km = 3000 m
Entonces, el valor a pagar por un recorrido de 3 kilómetros es:
f(3000) = 0.8 · 3000 + 250 = 2650
Por 3 kilómetros se pagan $2650.
I. FUNCIÓN LINEAL
Si queremos saber cuántos metros recorrió una persona si pagó
$2.250, se debe resolver la siguiente ecuación:
2250 = 0.8x + 250
/ -250
2000 = 0.8x
/ :0.8
2500 = x
Una persona que paga $2250. recorrió 2500 metros o 2.5
kilómetros.
I. FUNCIÓN LINEAL

Construcción de una Función Lineal conocidos valores de
ella:

Para construir una función lineal se deben conocer dos
relaciones distintas entre el valor de la variable y el valor de la
función, es decir:
(x , f(x )) y (x , f(x ))
2
1
O bien
si1 a f(x) le2 llamamos
y, entonces los pares quedan:
(x , y ) y (x , y )
1
1
2
2
Donde la función buscada será:
y – y 11= y2
- 1y 1 (x – x 1
2
1
x2 - x1
2
1
)
I. FUNCIÓN LINEAL

Ejemplo
Si se sabe que el agua se congela a 32º F ó 0º C y hierve a
212º F ó 100º C, ¿cómo se puede expresar los ºF como función
lineal de los ºC?
Solución:
Se tiene la siguiente información:
x y
x2 y 2
1
1
(0, 32) y (100, 212)
Cº : variable independiente (x)
ºF : variable dependiente (y)
I. FUNCIÓN LINEAL
Reemplazando en: y – y 1 = y 2 - y 1 (x – x 1 )
x 2 - x1
Se tiene:
y – 32 = 212 – 32 (x – 0)
100 – 0
y – 32 = 180 . x
100
y = 1.8· x + 32
Donde la función que representa los ºF respecto de ºC es.
f(x) = 1.8· x + 32
I. FUNCIÓN LINEAL
Se le llama crecimiento aritmético a la progresión cuyos
términos aumentan en una misma cantidad constante
llamada diferencia. Este crecimiento aritmético
gráficamente está representado por una recta con pendiente
positiva. Si la pendiente es negativa se habla de un
decrecimiento aritmético.
Ejemplo:
f (x) = 2x + 1
f (0) = 2· 0 + 1 = 1
+2
f (1) = 2· 1 + 1 = 3
+2
f (2) = 2· 2 + 1 = 5
+2
f (3) = 2· 3 + 1 = 7
I. FUNCIÓN LINEAL

Gráficamente
5
3
1
1
2
II. FUNCIÓN CUADRÁTICA

Son de la forma:
f(x) = ax² + bx + c

Gráfica:
Siempre es una parábola, dependiendo su forma y
la ubicación de sus coeficientes a, b y c.
II. FUNCIÓN CUADRÁTICA

Concavidad:
El coeficiente a de la función cuadrática indica si la parábola es
abierta hacia arriba o hacia abajo.
y
0
y
x
a > 0, Abierta hacia arriba
0
x
a < 0, Abierta hacia abajo
II. FUNCIÓN CUADRÁTICA

Eje de simetría y vértice:
El eje de simetría es aquella recta paralela al eje Y y que pasa
por el vértice de la parábola.
El vértice está dado por:
Vértice = -b , f
2a
-b
2a
=
-b , 4ac – b²
2a
4a
II. FUNCIÓN CUADRÁTICA
Además, la recta x = -b , corresponde al Eje de simetría.
2a
y
y
a<0
a>0
-b
2a
_ b² - 4ac
4a
·
·
_ b² - 4ac
4a
-b
2a
x
0
x
II. FUNCIÓN CUADRÁTICA

Intersección con los ejes
 Intersección con el eje Y
El coeficiente c nos da el punto en el cual la parábola corta al
eje Y.
Sus coordenadas son (0, c)
y
c·
0
x
II. FUNCIÓN CUADRÁTICA

Intersección con el eje X
para determinar el o los puntos donde la parábola corta al
eje X, es necesario conocer el valor del discriminante de la
función cuadrática.
Se define el discriminante como:
D = b² - 4ac
II. FUNCIÓN CUADRÁTICA

a) Si el D = 0, la parábola corta en un solo punto al eje X.
Y
a>0
(x = x , 0)
1
2
0
·
X
II. FUNCIÓN CUADRÁTICA

b) Si el D > 0, la parábola corta en dos puntos al eje X
Y
a>0
(x ,0) y (x , 0)
1
2
0
·
·
X
II. FUNCIÓN CUADRÁTICA

c) Si el D < 0, la parábola no corta al eje X.
Y
0
a>0
X
II. FUNCIÓN CUADRÁTICA

Naturaleza de las raíces de una ecuación de 2º grado
Si f(x) = 0, tendremos que ax² + bx + c = 0, llamada Ecuación de
2º grado en su forma general.
Toda ecuación de 2º grado posee dos soluciones, pudiendo ser
reales o imaginarias, las que vienen dadas por la expresión:
x = -b ±√b²- 4ac
2a
x 1 = -b ±√b²- 4ac
2a
x 2 = -b ±√b²- 4ac
2a
Estas soluciones, raíces o ceros de la ecuación
corresponden gráficamente a los puntos donde la función
f(x) = ax² + bx + c corta al eje X. Estos puntos tienen como
coordenadas (x 1 ,0) y (x2 , 0)
II. FUNCIÓN CUADRÁTICA

Tipos de soluciones
Dependen del valor del Discriminante
D = b² - 4ac
a)
Si D = 0, 2 soluciones reales iguales (x1 = y)
1
b)
Si D > 0, 2 soluciones reales distintas (x 1 y x2 € C, con x1 ≠ x 2)
c)
Si D < 0, 2 soluciones imaginarias distintas (x 1 y x 2 € C, con x 1 ≠ x 2)
II. FUNCIÓN CUADRÁTICA

Ejemplo:
Sea la ecuación de 2º grado: x² + 2x – 15 = 0. ¿Cuáles son las soluciones de
esta ecuación?
Sabemos que las soluciones de una ecuación de 2º grado vienen dadas por

x = -b ±√b²- 4ac
2a
En este caso
a=1
b=2
c = -15
x = -2 ±√2²- 4·1·(-15)
Luego,
2·1
x = -2 ±√4- 60
2
x = -2 ±√64
2
x = -2 ±8
2
Luego,
x = -2 + 8
x = -2 - 8
1
2
2
2
x =3
x = -5
1
2
III. FUNCIÓN PARTE ENTERA

Su valor, para cada número x € IR, es la parte entera de x y se
designa por [x]. Ésta se escribe:
f(x) = [x]

Dado un número real x, la función parte entera le asigna el mayor
entero que es menor o igual a x, es decir:
[x] ≤ x < [x+1]
Ejemplos:
[2,9] = 2
;[-7/2] = -4
;[5] = 5
;[√2] = 1
Todo número real está comprendido entre dos números
enteros, la parte entera de un número es el menor de
los números enteros entre los que está comprendido.
III. FUNCIÓN PARTE ENTERA
Obsérvese que esta función es constante en los intervalos
semiabiertos (semicerrados) de la forma [n, n + 1[ con n € Z.
Por tanto, los segmentos horizontales contienen sus
extremos izquierdos, pero no los derechos
IV. FUNCIÓN VALOR ABSOLUTO

El valor absoluto de un número x € IR, denotado por |x|, es
siempre un número real no negativo que se define:
x si x ≥ 0
f(x) = |x| =
-x si x < 0
Ejemplo:
|-3| = 3
|12| = 12
|-18| = 18
|-5,3| = 5,3
Si los números reales están representados
geométricamente en el eje real, el número |x| se
llama distancia de x al origen.
IV. FUNCIÓN VALOR ABSOLUTO

a indica el punto de traslación en el eje de las coordenadas.
IV. FUNCIÓN VALOR ABSOLUTO

b indica el punto de traslación en el eje de las abscisas.
IV. FUNCIÓN VALOR ABSOLUTO

Propiedades:

a. Si |x| ≤ a entonces -a ≤ x a; con a ≥ 0

b. Si |x| ≥ a entonces x ≥ a

c. |xy| = |x| · |y|

d. |x + y| ≤ |x| + |y|
ó
-x ≥ a
(Desigualdad Triangular)
IV. FUNCIÓN VALOR ABSOLUTO

La última propiedad se llama desigualdad triangular, pues,
cuando, se generaliza a vectores indica que la longitud de cada
lado de un triangulo es menor o igual a la suma de las longitudes
de los otros dos.
IV. FUNCIÓN VALOR ABSOLUTO

Ejercicios:
 Determinar el intervalo solución de las siguiente inecuación:

a.
|x – 3| ≤ 2
Aplicando la primera propiedad:
-2 ≤ x – 3 ≤ 2
-2 + 3 ≤ x ≤ 2 + 3
1≤x≤5
x € [1, 5]
IV. FUNCIÓN VALOR ABSOLUTO
La Respuesta correcta es B
IV. FUNCIÓN VALOR ABSOLUTO
La Respuesta correcta es D
V. FUNCIÓN EXPONENCIAL

Es la función inversa del logaritmo natural y se denota
equivalentemente como: x
e^x o x
exp(x)
La función exponencial f con base a se define como
x
f(x) = a
Si a > 0 ^ a ≠ 1, x € IR
V. FUNCIÓN EXPONENCIAL

Propiedades:

El dominio de la función exponencial está dado por los
números IR.

El recorrido de la función exponencial está dado por los IR*.

El punto de intersección de la función con el eje Y es (0, 1).

La función no intercepta el eje X.
V. FUNCIÓN EXPONENCIAL

Crecimiento y decrecimiento exponencial:

Si a > 1, f(x) es creciente en todo IR.
Mientras más grande el número de la base, la línea
estará más cerca del eje Y.
V. FUNCIÓN EXPONENCIAL

Crecimiento y decrecimiento exponencial:

Si 0 < a < 1, f(x) es decreciente en IR
V. FUNCIÓN EXPONENCIAL

Ejercicio:
Determinar la función que representa en número de bacterias que hay en
una población después de x horas si se sabe que inicialmente había 10.000
bacterias y que la población se triplica cada una hora.
Solución:

Cantidad inicial
= 10.000
Después de una hora = 10.000 · 3 = 30.000
Después de dos horas = 10.000 · 3 · 3 = 90.000
x
… Después de x horas = 10.000· 3
Por lo tanto, siendo x el número de horas que pasan desde el inicio del
estudio, la cantidad de bacterias se representa por la función:
f(x) = 10.000 · 3
x
V. FUNCIÓN LOGARÍTMICA

La inversa de una función exponencial de base a se llama
función logarítmica de base a y se representa por log a.

Está dada por la siguiente ecuación:
y = log ax
si
y
x=a
V. FUNCIÓN LOGARÍTMICA

Propiedades

El dominio de la función logarítmica está dado por los
números IR, la función no está definida para x ≤ 0.

El punto de intersección de la función con el eje X es (1, 0).

La función no intercepta el eje Y.
V. FUNCIÓN LOGARÍTMICA

Crecimiento y decrecimiento Logarítmico:

Si a > 1, f(x) = loga x es creciente para x > 0.
V. FUNCIÓN LOGARÍTMICA

Crecimiento y decrecimiento Logarítmico:

Si 0 < a < 1, f(x) = loga x es decreciente para x > 0.
V. FUNCIÓN LOGARÍTMICA

Ejercicios:

Dado los valores: log 2 = 0.3010 y log 3 = 0.4771. Entonces, en la función
f(x) = log x, determine f(6).
Solución:
f(6) = log (6)
Donde
log 6 = log (2 · 3)
Por Propiedad
log (2 · 3) = log 2 + log 3
= 0.3010 + 0.4771
= 0.7781
Por lo tanto:
Si f(x) = log x, entonces f(6) = 0.7781
V. FUNCIÓN LOGARÍTMICA
La Respuesta correcta es D