GEOMETRÍA TALLER Nº2: “Vaciando líquido con cuerpos

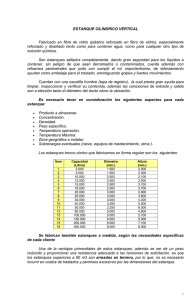
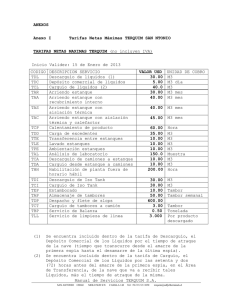
GEOMETRÍA
TALLER Nº2:
“Vaciando líquido con cuerpos geométricos”
Nombre: ____________________________________________ Sección: _________
Instrucciones:






Taller con nota, para resolver en grupos de máximo tres alumnos.
Cada grupo debe entregar un informe con el desarrollo del Taller para su evaluación y
todas las hojas con los enunciados del problema planteado.
Se permite el uso de calculadora, cuadernos y libros. Pero no de celulares u otros
equipos tecnológicos.
Tiempo máximo asignado: 80 minutos.
No se permiten consultas los primeros 30 minutos.
Este Taller será evaluado con una escala de 1 a 7. El puntaje total del Taller es de 60
puntos. La nota 4,0 se obtiene con el 60% del puntaje (36 puntos).
Don Manuel, profesor de matemática jubilado, luego de estudiar los cuerpos
geométricos con su nieta Javiera le propone el siguiente desafío:
Si se desea vaciar el contenido líquido de un
estanque con forma
de prisma recto, base
hexagonal, de arista basal 40 cm y altura 120 cm
a un estanque cilíndrico de radio 35 cm ¿cuál debe
ser la altura del nuevo estanque?, ¿Cuántas veces
se utilizará un embudo cónico a su máxima
capacidad de radio 15 cm y altura 30 cm para
vaciar el líquido de un estanque a otro?. El dueño
de los estanques desea pintarlos ¿en cuál de los
dos estanques utilizará menos pintura?
Como te habrás dado cuenta, Javiera tiene tres interrogantes que
responder, y tú la ayudarás en su desafío. Para esto te aconsejo ir paso a paso
calculando y respondiendo las preguntas planteadas. Trabaja todas las
cantidades en cm y aproxima los decimales a dos cifras decimales.Éxito!!
GEOMETRÍA
Para preguntas 1 y 2 recuerda que:
𝐕 𝐩𝐫𝐢𝐬𝐦𝐚 = Á𝐫𝐞𝐚 𝐛𝐚𝐬𝐚𝐥 × 𝐚𝐥𝐭𝐮𝐫𝐚
Á ∆𝐞𝐪𝐮𝐢𝐥á𝐭𝐞𝐫𝐨 =
𝐥𝐚𝐝𝐨𝟐 × √𝟑
𝟒
𝑽 𝒄𝒊𝒍𝒊𝒏𝒅𝒓𝒐 = 𝝅 × 𝒓𝟐 × 𝐡
𝑽𝒄𝒐𝒏𝒐 =
𝟏
× 𝝅 × 𝒓𝟐 × 𝐡 =
𝟑
𝑪𝒐𝒏𝒔𝒊𝒅𝒆𝒓𝒂𝒓 𝝅 = 𝟑, 𝟏𝟒
1. Si se desea vaciar el contenido líquido de un estanque con forma de
prisma recto, base hexagonal, de arista basal 40 cm y altura 120
cm a un estanque cilíndrico de radio 35 cm ¿cuál debe ser la altura
del nuevo estanque?
(Considerar que la cantidad de líquido que hay en el prisma alcanza
la máxima altura de este.)
30 puntos
2. ¿Cuántas veces se utilizará un embudo cónico a su máxima
capacidad de radio 15 cm y altura 30 cm para vaciar el líquido?
10 puntos
Para pregunta 3, recuerda que:
Á 𝐩𝐫𝐢𝐬𝐦𝐚 = 𝐒𝐮𝐦𝐚 𝐝𝐞 𝐥𝐚𝐬 Á𝐫𝐞𝐚𝐬 𝐝𝐞 𝐬𝐮𝐬 𝐜𝐚𝐫𝐚𝐬
Á 𝐜𝐢𝐥𝐢𝐧𝐝𝐫𝐨 = 𝟐 × 𝛑 × 𝐫 × 𝐡 + 𝟐 × 𝛑 × 𝐫 𝟐
𝑪𝒐𝒏𝒔𝒊𝒅𝒆𝒓𝒂𝒓 𝝅 = 𝟑, 𝟏𝟒
3. El dueño de los estanques desea pintarlos ¿en cuál de los dos
estanques utilizará menos pintura?
20 puntos