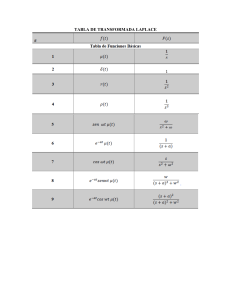
TRANSFORMADA DE LAPLACE Y SU INVERSA 6 pag. Descargado por Christian Chu ([email protected]) Encuentra más documentos en TRANSFORMADA DE LAPLACE Y SU INVERSA 2019 Objetivos de esta guía Analizar señales y sistemas en tiempo continuo para sistemas lineales e invariantes en el tiempo Transformada de Laplace de Laplace y transformada inversa de Laplace. Aplica la transformada de Laplace y/o su inversa por medio del uso de tablas de transformadas a diferentes funciones. Página 1 de 6 Descargado por Christian Chu ([email protected]) Encuentra más documentos en 2. FUNDAMENTO TEÓRICO TRANSFORMADA DE LAPLACE Consideremos una función del tiempo 𝑓(𝑡) definida para 𝑡 > 0. Si la función es una función seccionalmente continua en el intervalo 0 < 𝑡 < 𝑇 y de orden exponencial para 𝑡 > 𝑇, su transformada de Laplace se define como: TABLA DE TRANSFORMADAS Por integración directa se puede verificar la tabla que se muestra a continuación: Dominio de tiempo Dominio de la frecuencia 𝛿(𝑡) 1 𝐾𝑢(𝑡) 1 𝑒𝑎𝑡𝑢(𝑡) 𝑠−𝑎 𝑠𝑒𝑛(𝜔𝑡)𝑢(𝑡) 𝑐𝑜𝑠(𝜔𝑡)𝑢(𝑡) 𝑡𝑛𝑢(𝑡) PROPIEDADES DE LA TRANSFORMADA Propiedad Linealidad Traslación lineal 𝜔 𝑠>𝑎 𝑠2 + 𝜔2 𝑠 𝑛! 𝑠𝑛 +1 𝑠2 + 𝜔2 𝑛 = 0,1,2,3, … Dominio de tiempo Dominio de la frecuencia 𝑎𝑓(𝑡) + 𝑏𝑔(𝑡) 𝑎𝐹(𝑠) + 𝑏𝐺(𝑠) 𝑒𝑎𝑡𝑓(𝑡) 𝐹(𝑠 − 𝑎) Página 2 de 6 Descargado por Christian Chu ([email protected]) Encuentra más documentos en 𝑓(𝑡 − 𝑎)𝑢(𝑡 − 𝑎) Traslación real Corolario Derivada en el tiempo 𝑒−𝑎𝑠𝐹(𝑠) 𝑓(𝑡)𝑢(𝑡 − 𝑎) 𝑒−𝑎𝑠𝐿{𝑓(𝑡 + 𝑎)} 𝑓(𝑛)(𝑡) 𝑠𝑛𝐹(𝑠) − 𝑠𝑛−1𝑓(0) − ⋯ − 𝑓(𝑛−1)(0) 𝑠𝐹(𝑠) − 𝑓(0) 𝑓′(𝑡) Corolario Integral en el tiempo 𝑡 ∫ 𝑓(𝜏)𝑑𝜏 0 Multiplicación por t −𝐹′(𝑠) 𝑡𝑓(𝑡) 𝑡(𝑛)𝑓(𝑡) Corolario (−1)𝑛𝐹(𝑛)(𝑠) 𝑓(𝑡) = 𝑓(𝑡 − 𝑛𝑇) Función periódica 𝑡>0 𝑇 ∫0 𝑒−𝑠𝑡𝑓(𝑡)𝑑𝑡 1 − 𝑒−𝑇𝑠 𝑇 ∫ 𝑒−𝑠𝑡𝑓(𝑡)𝑑𝑡 = 𝐿{𝑓(𝑡)} − 𝑒−𝑇𝑠𝐿{𝑓(𝑡 + 𝑇)} 0 TRANSFORMADA INVERSA DE LAPLACE Dada una función en el dominio de la frecuencia 𝐹(𝑠), su inversa es una función de tiempo y viene dada por: 𝑓(𝑡) = 𝐿−1{𝐹(𝑠)} TABLA DE TRANSFORMADAS A partir de la tabla de transformadas directas se obtiene la siguiente tabla que se repite por comodidad. Dominio de la frecuencia Dominio de tiempo 1 𝛿(𝑡) 1 𝑠−𝑎 𝑠>𝑎 𝐾𝑢(𝑡) 𝑒𝑎𝑡𝑢(𝑡) Página 3 de 6 Descargado por Christian Chu ([email protected]) Encuentra más documentos en 1 𝑠2 + 𝜔2 𝑠 𝑐𝑜𝑠(𝜔𝑡)𝑢(𝑡) 𝑠2 + 𝜔2 PROPIEDADES DE LA TRANSFORMADA 𝑡 𝑛 −1 𝑢 (𝑡) (𝑛 − 1)! Propiedad Dominio de la frecuencia Dominio de tiempo Linealidad 𝑎𝐹(𝑠) + 𝑏𝐺(𝑠) 𝑎𝑓(𝑡) + 𝑏𝑔(𝑡) 𝑒−𝑎𝑠𝐹(𝑠) 𝑓(𝑡 − 𝑎)𝑢(𝑡 − 𝑎) 𝐹(𝑠 − 𝑎) Traslación lineal Traslación real 𝑒−𝑎𝑠𝐿{𝑓(𝑡 + 𝑎)} Multiplicación por 𝑠 𝑠𝐹(𝑠) División por 𝑠 𝑒𝑎𝑡𝑓(𝑡) 𝑓(𝑡)𝑢(𝑡 − 𝑎) 𝑓′(𝑡) 𝑠𝑖 𝑓(0) = 0 𝑡 ∫ 𝑓(𝜏)𝑑𝜏 0 Derivada en el dominio de 𝑠 𝐹′(𝑠) 3. OBJETIVO −𝑡𝑓(𝑡) Aplicar la transformada de Laplace y/o su inversa, por medio del uso de tablas de transformadas, a diferentes funciones. 4. RECURSOS REQUERIDOS - Material bibliográfico de apoyo 5. PROCEDIMIENTO O METODOLOGÍA PARA EL DESARROLLO Ejercicios propuestos: 1. Calcule la transformada de Laplace de las siguientes funciones: Página 4 de 6 Descargado por Christian Chu ([email protected]) Encuentra más documentos en a) b) 𝑔(𝑡) = [𝑡 +𝑠𝑒𝑛(2𝑡)]𝑢(𝑡−𝜋) c) d) 𝑔(𝑡) = 𝑠𝑒𝑛2(𝑡)𝑢(𝑡−𝜋/2) e) f) 𝑔(𝑡) = 𝑠𝑒𝑛(𝜋𝑡)𝑢(𝑡−1) g) h) 𝑔(𝑡) = 𝑐𝑜𝑠(2𝑡)𝑢(𝑡−𝜋) 2. Calcule la transformada inversa de Laplace de las siguientes funciones: a) Calculando los coeficientes b) Sin calcular los coeficientes c) Calculando los coeficientes d) Sin calcular los coeficientes e) Sin calcular los coeficientes f) Sin calcular los coeficientes 3. Resuelva los problemas de valor inicial: a) b) c) d) e) f) 6. BIBLIOGRAFÍA - Zill, D. & Cullen, M. Ecuaciones Diferenciales. 3 ed. McGraw-Hill, 2008. 724 p ISBN 978-970-10-6514-3 Página 5 de 6 Descargado por Christian Chu ([email protected]) Encuentra más documentos en - Ambardar, A. (2002). Procesamiento de señales analógicas y digitales. 2 ed. México: Thomson. ISBN 970686038X Página 6 de 6 Descargado por Christian Chu ([email protected]) Encuentra más documentos en