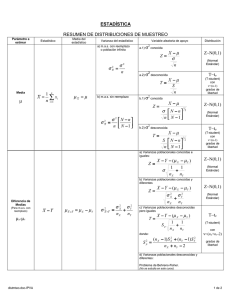
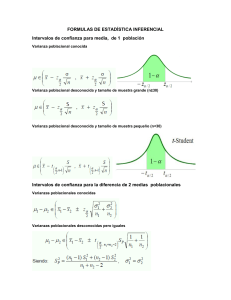
Facultad de Ingeniería Civil Eco. Nelly Andrés Casas. Semestre Académico 2021 - 1 Prueba de hipótesis para la varianza Prueba de hipótesis para la varianza Si se extrae una muestra aleatoria de tamaño n de una población normal con media µ y varianza σ2, y se calcula la varianza muestral, se obtiene el valor del estadístico s2 que se utilizará para conocer la σ2, mediante una variable aleatoria chi cuadrada con “n-1” grados de libertad. Concepto clave: En esta sección presentaremos métodos para probar una aseveración respecto de una desviación estándar poblacional(ơ) o varianza poblacional (ơ 2). Los métodos de esta sección utilizan la distribución chi cuadrada. Control de calidad: El mundo de la industria comparte esta meta común: mejorar la calidad reduciendo la variación. Los ingenieros de control de calidad desean asegurarse de que un producto tenga una media aceptable, pero también quieren producir artículos con una calidad consistente, eliminando los defectos. Contrastes sobre la varianza Media desconocida Ensayo de hipótesis: Estadístico de contraste Criterio de rechazo Contrastar la hipótesis de que la varianza de una población normal es 3, si con una muestra de 16 elementos la varianza muestra es 4, siendo α = 0.05 Solución: = 0.025 1. Ensayo de hipótesis Ho: σ2 = 3 Ha: σ2 ≠ 3 = 0.025 2. Elegimos el modelo probabilístico: 27.4784 6.1621 4. Tomar una decisión e interpretar (16 – 1) 4 Χ2 = Decisión: Si, = 20 3 3. Calcular el valor critico: Χ21-α/2; =15 = Χ21-0.05/2; =15 Χ20.975;=15 = 6.1621 Χ2α/2; =15 = Χ20.05/2; =15 Χ20.025=15 = 27.4784 Se rechaza Ho. Pero como: SE ACEPTA HO Conclusión: No hay suficiente evidencia para rechazar Ho. : Un fabricante de baterías garantiza que su producto dura en promedio 2,5 años con una desviación estándar de 0,8 años. Si se toma una muestra aleatoria de 8 baterías y resultó que = 2.8 y la S = 1.2, ¿con la evidencia tomada tiene razón el fabricante respecto a la desviación estándar poblacional? Utilice un nivel de significancia de 0,01. Solución: 1. Datos: µ = 2.5 años , ơ = 0.8 años, 2. Ensayo de hipótesis Ho: σ2 = 0.8 Ha: σ2 > 0.8 n = 8 baterías, = 2.8, S = 1.2 gl = 8 – 1 = 7 5. Tomar una decisión e interpretar Puesto que el estadístico de prueba no está en la región crítica, no rechazamos la hipótesis nula 4. Calcular el valor critico: α = 0.01, y v = 7. El valor crítico será: Χ2α = 18.48 3. Elegimos el modelo probabilístico: 0.01 Χ2 α = 18.48 α = 0.01, INTERPRETACIÓN No hay suficiente evidencia para sustentar la aseveración de que la desviación estándar. La Asociación de Jóvenes Empresarios (Aje) ha fabricado latas de bebidas de cola con cantidades que tienen una desviación estándar de 0.051 onzas. Se prueba una nueva máquina embotelladora y una muestra aleatoria simple de 24 latas produce las cantidades (en onzas) tienen una desviación estándar de 0.039 oz. Utilice un nivel de significancia de 0.05 para probar la aseveración de que las latas de bebidas de cola de la nueva máquina tienen cantidades con una desviación menor que 0.051 oz. . Solución: 1. Datos: ơ = 0.051 onzas. n = 24 latas 2. Ensayos de hipótesis: Ho: ơ = 0.051 H1: ơ < 0.051 S = 0.039onzas. α = 0.05 4. Calcular el valor critico de χ2: α = 0.05, = (n – 1) = 23 Rechazo Método tradicional de prueba de hipótesis: α = 0.05 0.95 3. Estadístico de prueba Si, se rechaza Ho 5. Tomar una decisión e interpretar (24 – 1)0.0392 χ2 = = 13.450 0.0512 No Rechazo Como, Χ2exp > Χ21- α; , es decir, 13.450 > 13.09, se acepta Ho. 0.95 13.09 No hay suficiente evidencia para sustentar la aseveración de que la desviación estándar de las cantidades con la nueva máquina sea menor que 0.051 onzas. Quizás la nueva máquina produce cantidades de bebida de cola que son más consistentes, con una desviación estándar menor que 0.051 oz, pero aún no tenemos evidencia suficiente para sustentar esa aseveración. Método del valor P 2p = 13.450 α = 0.05 = (n – 1) = 23 X2 C 13.091 = 13.450 0.95 14.848 0.90 lo que significa que el área a la derecha del estadístico de prueba está entre 0.95 y 0.90. Valor P= 0.10 0.90 13.450 Valor P ≤ α rechazar Ho al nivel α Valor P > α No rechazar Ho al nivel α P-valor = 0.10 > 0.05 No rechazar Ho Una vez más, el método tradicional y el método del valor P son equivalentes en el sentido de que siempre conducen a la misma conclusión. Para cumplir con la normativa, la varianza del nivel de impurezas en tanto por ciento en los envíos de un cierto producto químico no puede superar el valor 4. Una muestra aleatoria de veinte envíos ha proporcionado una cuasi-varianza muestral del nivel de impurezas de 5.62. a) Lleva a cabo un contraste de hipótesis adecuado (α = 0.1). b) Calcula la potencia del contraste. ¿Cuál es la potencia para σ21 = 7? c) ¿Qué tamaño muestral garantizaría una potencia de 0.9 para σ21 = 7? Solución: X = “nivel de impurezas del producto en un envío (en %)” X ∼ N(µ, σ2 ) b. Ensayo de hipótesis: MAS n=20 Muestra: s2 = 5.62 α = 0.1 Estadístico del contraste: Ho : σ2 ≤ σ20 = 4 H1 : σ2 > 4 α = 0.1, entonces valor critico: 27.2 (20 – 1)5.62 χ2 = = 26.695 4 No rechazamos Ho α = 0.1 No tenemos suficientes pruebas para sostener la información de que el nivel de impurezas del producto en un envió sea mayor a 4 27.2 Comparación de la variación en dos muestras Puesto que la característica de variación entre los datos es extremadamente importante, esta sección presenta la prueba F para comparar dos varianzas (o desviaciones estándar) poblacionales utilizando dos muestras. La distribución F, se utiliza para la prueba F. Desventaja: La prueba F para comparar dos varianzas (o desviaciones estándar) poblacionales es muy sensible a las desviaciones que se alejan de la distribución normal. Prueba F para comparar varianzas Utilizaremos varianzas muestrales (o desviaciones estándar) para comparar dos varianzas (o desviaciones estándar) poblacionales Pruebas de hipótesis para dos varianzas poblacionales Medias desconocidas Para esta prueba de hipótesis solo desarrollaremos el caso bilateral debido a que esta prueba indicará si dos muestras independientes provienen de poblaciones con varianzas homogéneas o heterogéneas lo que será necesario saber al realizar prueba de hipótesis para dos promedios. Se realiza un estudio de prácticas de prescripción. El propósito es analizar la prescripción de eritromicina un fármaco importante, potencialmente tóxico y comúnmente utilizado. El nivel de dosificación para los mayores de 64 años debe ser menor que el de personas más jóvenes. Se extraen muestras independientes de cada grupo y se obtiene el nivel de dosificación para cada paciente seleccionado. Los resultados son: ¿Se puede considerar que la dispersión en ambas poblaciones es la misma? Con α = 0.05 Solución: X: Cantidad de eritromicina en pacientes > 64 años. Y: Cantidad de eritromicina en pacientes ≤ 64 años. 2. Estadístico de contraste: Rechazamos Ho (0.102)2 1. Contraste de Hipótesis: Ho: σ2X = σ2Y H1: σ2X ≠ σ2Y 5. Tomar una decisión e interpretar F= = 2.25 Las varianzas poblacionales son diferentes (0.068)2 4. Calcular el valor critico de F: 0.025 α = 0.05, F(α/2; =40,28) = F(0.05/2; =40,28) F (0.025; ;=40,28) = 2.02 0.095 F(0.975;40;28) 0.025 F(0.025;40,28) = 2.02 Los pesos (en libras) de muestras de Coca clásica y Pepsi clásica se encuentan en una tabla y los estadísticos muestrales se resumen en la tabla adjunta. Utilice un nivel de significancia 0.05 para probar la aseveración de que los pesos de Coca clásica y los pesos de Pepsi clásica tienen la misma desviación estándar Solución: REQUISITO: las poblaciones son independientes entre sí. las muestras sugieren que provienen de una población con una distribución aproximadamente normal 1. Contraste de Hipótesis: Ho: σ21 = σ22 H1: σ21 ≠ σ22 2. Estadístico de contraste: Puesto que esta prueba implica dos varianzas poblacionales, utilizamos la distribución F. (0.0107507)2 F= = 1.7339 (0.005701)2 0.025 0.025 4. Calcular el valor critico de F: α = 0.05, 1.96 F(α/2; =36,36) = F(1-0.05/2; =36,36) F (0.025; ;=36,36) = 1.96 F(1-α/2; =36,36) = F(1-0.05/2; =36,36) F (0.975;=36,36) Decisión: no rechazamos la Ho. 0.025 0.975 Conclusión: No existe suficiente evidencia para justificar el rechazo de la aseveración de que las dos desviaciones estándar son iguales. Sin embargo, debemos reconocer que la prueba F es sumamente sensible a distribuciones que no son normales, de manera que podría parecer que esta conclusión indica que no existe una diferencia significativa entre las desviaciones estándar poblacionales, cuando realmente existe una diferencia que quedó oculta debido a distribuciones no normales. Una empresa de bebidas energizantes posee dos tipos de bebidas en el mercado: Energy Aid y Energy Pro. El ingeniero de control de calidad desea evaluar el contenido de refresco en los dos tipos de energizantes, para el análisis se seleccionó 17 latas de refresco Energy Aid que posee una media de 17.2 onzas, con una desviación estándar de 3.2 onzas, y trece refrescos Energy Pro de donde se obtuvo una media de 18.1 onzas y una desviación estándar de 2.7 onzas. Asumiendo que el contenido de refrescos se distribuye normalmente, ¿se puede afirmar con 6% de significación que las varianzas de los contenidos son iguales? Solución: 1. Variables aleatorias: X1: Contenido de una lata de refresco Energy Aid (onzas), X2: Contenido de una lata de refresco Energy Pro (onzas), 2. Ensayo de Hipótesis: Ho: σ21 = σ22 H1: σ21 ≠ σ22 3. Estadístico de prueba: 4. Valores críticos: α = 0.06 α/2 =0.03; F(1- α/2,16,12) = F (α/2,16,12)= Valor crítico inferior: INV.F.CD(0.97; 16, 12) = 0.3618 Valor crítico superior: INV.F.CD(0.04; 16, 12) = 3.000959 5- Decisión y conclusión Decisión: No se Rechaza Ho Conclusión: No existe suficiente evidencia estadística, con un nivel de significación del 6%, para afirmar que las varianzas son diferentes. Es decir, existe homogeneidad de varianzas. Un grupo de empresarios inauguró el año pasado dos restaurantes en las zonas más representativas de Lima. Después de un año de actividades deciden medir y comparar, el nivel de ingresos de ambos locales para lo cual eligen muestras aleatorias de los ingresos mensuales. La información se presenta en la siguiente tabla: Se puede afirmar que el local 1 tiene ingresos promedio mayores que los del local 2. Asuma que el consumo mensual tiene distribución normal. Use un nivel de significación del 6%. Solución: 1. Variables aleatorias: X1: Ingreso mensual del local 1 X2: Ingreso mensual del local 2 Dado que las varianzas poblacionales son desconocidas, el primer paso consiste en realizar una prueba de hipótesis para determinar si las varianzas son homogéneas o no. En Excel: Datos, Análisis de datos, Prueba F para varianzas de dos muestras 4. Valores críticos: α = 0.06 α/2 =0.03; F(1- α/2,16,12) =0.26677 F (α/2,16,12)= 3.5702 Valor crítico inferior: INV.F.CD(0.97; 9, 10) = 0.2677 2. Ensayo de Hipótesis: 3. Estadístico de prueba: Ho: σ21 = σ22 H1: σ21 ≠ σ22 Valor crítico superior: INV.F.CD(0.03; 9, 10) = 3.5702 5- Decisión y conclusión Decisión: No se Rechaza Ho Conclusión: No existe suficiente evidencia estadística, con un nivel de significación del 6%, para afirmar que las varianzas son diferentes. Con este resultado afirmamos que existe homogeneidad de varianzas. Habiendo probado que las varianzas son homogéneas, ahora pasamos a probar si el local 1 tiene ingresos promedio mayores que los del local 2 1. Ensayo de Hipótesis: 2. Estadístico de prueba: 2.713154062 3. Valores críticos: α = 0.06 1.627972318 4- Decisión y conclusión El valor calculado del estadístico de prueba, Tc = 2.7132, cae en la región de rechazo Decisión: Se Rechaza Ho Conclusión: Existe suficiente evidencia estadística, con un nivel de significación del 6%, para afirmar que el local 1 tiene en promedio, mayores ingresos mensuales que el local 2 Una empresa fabrica, en sus dos plantas situadas en Atlanta y Dallas, impresoras y faxes. Con el fin de medir los conocimientos que tienen los empleados de estas plantas acerca de la calidad de los productos producidos, se toma una muestra aleatoria de empleados de cada fábrica y se les aplica una evaluación de calidad. Los resultados se muestran en el siguiente cuadro. ¿Se puede afirmar que la puntuación promedio obtenida en el examen de calidad no es la misma para las dos fábricas? Use α = 0.05 COMPONENTES DE UNA SERIE Tendencia: Movimientos persistentes ascendentes o descendentes a través del tiempo. Variaciones estacionales. Fluctuaciones periódicas en periodos de tiempo cuya frecuencia es menor a un año, aproximadamente en las mismas fechas y casi con la misma intensidad. Movimientos o variaciones cíclicas. Los movimientos se consideran cíclicos, solo si se producen en un intervalo de tiempo superior al año. Movimientos irregulares o al azar. movimientos esporádicos o de corto plazo.