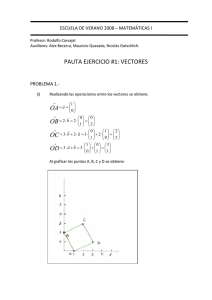
Ejercicios de algebra lineal Espacios vectoriales-matriz de cambio Sea 𝑉 = 𝑅2 , 𝐹 = 𝑅, con las operaciones definidas por 𝑥1 , 𝑦1 + 𝑥2 , 𝑦2 = 𝑥1 + 𝑥2 + 1, 𝑦1 + 𝑦2 + 1 𝑟 𝑥, 𝑦 = 𝑟 + 𝑟𝑥 − 1, 𝑟 + 𝑟𝑦 − 1 Analizar si V es un espacio vectorial. Veamos si se verifican los 08 axiomas A1. 𝑥1 , 𝑦1 + 𝑥2 , 𝑦2 = 𝑥1 + 𝑥2 + 1, 𝑦1 + 𝑦2 + 1 = 𝑥2 + 𝑥1 + 1, 𝑦2 + 𝑦1 + 1 = 𝑥2 , 𝑦2 + 𝑥1 , 𝑦1 A2. 𝑥1 , 𝑦1 + 𝑥2 , 𝑦2 + 𝑥3 , 𝑦3 = 𝑥1 , 𝑦1 + 𝑥2 , 𝑦2 + 𝑥3 , 𝑦3 Por un lado 𝑥1 , 𝑦1 + 𝑥2 , 𝑦2 + 𝑥3 , 𝑦3 = 𝑥1 + 𝑥2 + 1, 𝑦1 + 𝑦2 + 1 + 𝑥3 , 𝑦3 = 𝑥1 + 𝑥2 + 1 + 𝑥3 + 1, 𝑦1 + 𝑦2 + 1 + 𝑦3 + 1 = 𝑥1 + 𝑥2 + 𝑥3 + 2, 𝑦1 + 𝑦2 + 𝑦3 + 2 (1) Por otro lado 𝑥1 , 𝑦1 + 𝑥2 , 𝑦2 + 𝑥3 , 𝑦3 = 𝑥1 , 𝑦1 + 𝑥2 + 𝑥3 + 1, 𝑦2 + 𝑦3 + 1 = 𝑥1 + 𝑥2 + 𝑥3 + 1 + 1, 𝑦1 + 𝑦2 + 𝑦3 + 1 + 1 = 𝑥1 + 𝑥2 + 𝑥3 + 2, 𝑦1 + 𝑦2 + 𝑦3 + 2 (2) Comparando (1) y (2) se prueba la asociatividad. A3. Existencia del elemento neutro. Sea 𝑎, 𝑏 el elemento neutro, se debe verificar que 𝑥, 𝑦 + 𝑎, 𝑏 = 𝑥, 𝑦 𝑥 + 𝑎 + 1, 𝑦 + 𝑏 + 1 = 𝑥, 𝑦 ⟹ 𝑎, 𝑏 = (−1, −1) A4. Existencia del elemento opuesto. Sea 𝑚, 𝑛 el elemento opuesto, se debe verificar que 𝑥, 𝑦 + 𝑚, 𝑛 = −1, −1 𝑥 + 𝑚 + 1, 𝑦 + 𝑛 + 1 = −1, −1 ⟹ 𝑚, 𝑛 = −𝑥 − 2, −𝑦 − 2 A5. 1. 𝑥, 𝑦 = (𝑥, 𝑦) 1. 𝑥, 𝑦 = 1 + 𝑥 − 1,1 + 𝑦 − 1 = 𝑥, 𝑦 A6. 𝑟1 . 𝑟2 . 𝑥, 𝑦 𝑟1 . 𝑟2 . 𝑥, 𝑦 = 𝑟1 . 𝑟2 . 𝑥, 𝑦 = 𝑟1 . 𝑟2 + 𝑟2 𝑥 − 1, 𝑟2 + 𝑟2 𝑦 − 1 = 𝑟1 + 𝑟1 𝑟2 + 𝑟2 𝑥 − 1 − 1, 𝑟1 + 𝑟1 𝑟2 + 𝑟2 𝑦 − 1 − 1 = 𝑟1 + 𝑟1 𝑟2 + 𝑟1 𝑟2 𝑥 − 𝑟1 − 1, 𝑟1 + 𝑟1 𝑟2 + 𝑟1 𝑟2 𝑦 − 𝑟1 − 1 = 𝑟1 𝑟2 + 𝑟1 𝑟2 𝑥 − 1, 𝑟1 𝑟2 + 𝑟1 𝑟2 𝑦 − 1 = 𝑟1 . 𝑟2 . 𝑥, 𝑦 A7. 𝑟1 + 𝑟2 . 𝑥, 𝑦 = 𝑟1 𝑥, 𝑦 + 𝑟2 𝑥, 𝑦 Por un lado 𝑟1 + 𝑟2 . 𝑥, 𝑦 = 𝑟1 + 𝑟2 + 𝑟1 + 𝑟2 𝑥 − 1, 𝑟1 + 𝑟2 + 𝑟1 + 𝑟2 𝑦 − 1 (∗) Por otro lado 𝑟1 𝑥, 𝑦 + 𝑟2 𝑥, 𝑦 = = 𝑟1 + 𝑟1 𝑥 − 1, 𝑟1 + 𝑟1 𝑦 − 1 + 𝑟2 + 𝑟2 𝑥 − 1, 𝑟2 + 𝑟2 𝑦 − 1 = 𝑟1 + 𝑟1 𝑥 − 1 + 𝑟2 + 𝑟2 𝑥 − 1 + 1, 𝑟1 + 𝑟1 𝑦 − 1 + 𝑟2 + 𝑟2 𝑦 − 1 + 1 = 𝑟1 + 𝑟2 + 𝑟1 𝑥 + 𝑟2 𝑥 − 1, 𝑟1 + 𝑟2 + 𝑟1 𝑦 + 𝑟2 𝑦 − 1 Comparando (*) y (**) se ve que se cumple A7. (∗∗) A8. 𝑟 𝑥1 , 𝑦1 + 𝑥2 , 𝑦2 = 𝑟. 𝑥1 , 𝑦1 + 𝑟. 𝑥2 , 𝑦2 Por un lado 𝑟 𝑥1 , 𝑦1 + 𝑥2 , 𝑦2 = 𝑟 𝑥1 + 𝑥2 + 1, +𝑦1 + 𝑦2 + 1 = 𝑟 + 𝑟 𝑥1 + 𝑥2 + 1 − 1, 𝑟 + 𝑟 𝑦1 + 𝑦2 + 1 − 1 = 2𝑟 + 𝑟𝑥1 + 𝑟𝑥2 − 1,2𝑟 + 𝑟𝑦1 + 𝑟𝑦2 − 1 Por otro lado 𝑟. 𝑥1 , 𝑦1 + 𝑟. 𝑥2 , 𝑦2 = 𝑟 + 𝑟𝑥1 − 1, 𝑟 + 𝑟𝑦1 − 1 + 𝑟 + 𝑟𝑥2 − 1, 𝑟 + 𝑟𝑦2 − 1 = 𝑟 + 𝑟𝑥1 − 1 + 𝑟 + 𝑟𝑥2 − 1 + 1, 𝑟 + 𝑟𝑦1 − 1 + 𝑟 + 𝑟𝑦2 − 1 + 1 = 2𝑟 + 𝑟𝑥1 + 𝑟𝑥2 − 1,2𝑟 + 𝑟𝑦1 + 𝑟𝑦2 − 1 Se cumplen los 08 axiomas. Ejemplo 2 𝑥 𝑦 Sea 𝑉 = 𝑀2×2 , 𝐹 = 𝑅, 𝑊 = −𝑦 𝑧 ; 𝑥, 𝑦, 𝑧 ∈ 𝑅 a)Analizar si W es un subespacio de V. b)Calcular la dimensión de W. Veamos si W es cerrado con respecto a la operación + 𝑥 𝑦 𝑎 𝑏 Sean −𝑦 𝑧 , ∈𝑊 −𝑏 𝑐 𝑥 𝑦 𝑥+𝑎 𝑦+𝑏 𝑎 𝑏 −𝑦 𝑧 + −𝑏 𝑐 = −(𝑦 + 𝑏) 𝑧 + 𝑐 ∈ 𝑊 Veamos si W es cerrado con respecto a la operación “.” 𝑥 𝑦 𝑥 𝑦 𝑟𝑥 𝑟𝑦 Sea 𝑟 ∈ 𝑅, −𝑦 𝑧 ∈ 𝑊 ⟹ 𝑟. −𝑦 𝑧 = −𝑟𝑦 𝑟𝑧 ∈ 𝑊 Luego W es un subespacio de 𝑀2×2 Hallemos la dimensión de W 𝑥 −𝑦 𝑥 −𝑦 𝑦 𝑥 𝑧 = 0 𝑦 1 𝑧 =𝑥 0 0 0 + −𝑦 0 0 0 +𝑦 0 −1 𝑦 0 0 + 0 0 𝑧 1 0 0 +𝑧 0 0 1 Una base para W es 𝐵= 1 0 0 1 0 , , 0 0 −1 0 0 Luego dim 𝑊 = 3 0 1 Que 𝐻1 𝑦 𝐻2 son sub espacios se procede como el ejemplo anterior Calculemos 𝐻 = 𝐻1 ∩ 𝐻2 0 𝑦 −𝑏 𝑎 𝐻1 : , 𝐻2 : 𝑧 𝑤 𝑎 𝑏 Las matrices de H son de la forma −0 𝑎 0 1 =𝑎 𝑎 0 1 0 Una base para H es 0 1 𝐵= 1 0 La dim 𝐻 = 1 Ejercicios 1. ¿Cuál es la dimensión del subespacio de 𝑹𝟑 generado por los vectores a) Los vectores 𝟐, 𝟏, −𝟏 , 𝟑, 𝟐, 𝟏 , 𝟏, 𝟎, −𝟑 ? b) Los vectores 𝟏, −𝟏, 𝟐 , 𝟎, 𝟐, 𝟏 , −𝟏, 𝟎, 𝟏 ? 2. ¿Cuál es la dimensión del subespacio de 𝑹𝟒 generado por los vectores a) Los vectores 𝟏, 𝟎, 𝟐, −𝟏 , 𝟑, −𝟏, −𝟐, 𝟎 , 𝟏, −𝟏, −𝟔, 𝟐 , 𝟎, 𝟏, 𝟖. −𝟑 ? 𝟏 𝟏 𝟐 𝟐 b) Los vectores − , , 𝟑, −𝟏 , 𝟏 𝟏 , 𝟎, 𝟏, − 𝟐 𝟐 , 𝟏, 𝟏, 𝟏𝟎, −𝟒 ? 3. Sea W el conjunto de todos los polinomios 𝑷𝒏 cuya segunda derivada es cero; probar que W es un subespacio de 𝑷𝒏 y encontrar una base para W. 4. Sea W el conjunto de todos los polinomios 𝑷𝒏 tales que 𝒑 𝟏 = 𝒑′ 𝟏 = 𝟎; probar que W es un subespacio de 𝑷𝒏 y encontrar una base para W. 5. Encontrar la dimensión del sub espacio de 𝑪 −𝝅, 𝝅 generado por los vectores 𝟏, 𝐬𝐢𝐧 𝒙 , 𝐜𝐨𝐬 𝒙 , 𝒔𝒊𝒏𝟐 𝒙, 𝒄𝒐𝒔𝟐 𝒙 𝟑 𝟐 𝟏 𝟓 𝟐 𝟐 𝟑 𝟐 6. Sea 𝑩 = 𝟏, 𝒙. 𝒙𝟐 − , 𝒙𝟑 − 𝒙 a) Demostrar que B es una base de 𝑷𝟑 b) Hallar las coordenadas de 𝒙𝟐 y𝒙𝟑 . 7. Encontrar una base de 𝑹𝟒 con respecto a la cual el vector −𝟑, 𝟏, 𝟐 − 𝟏 𝟏 𝟏 tenga las coordenadas . 𝟏 𝟏 8. Suponiendo que los vectores 𝜶𝟏 , 𝜶𝟐 , 𝜶𝟑 son linealmente independientes en el espacio vectorial V, demostrar que 𝜶𝟏 , +𝜶𝟐 , 𝜶𝟏 , +𝜶𝟑 , 𝜶𝟐 +𝜶𝟑 son linealmente independientes.