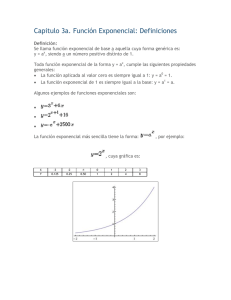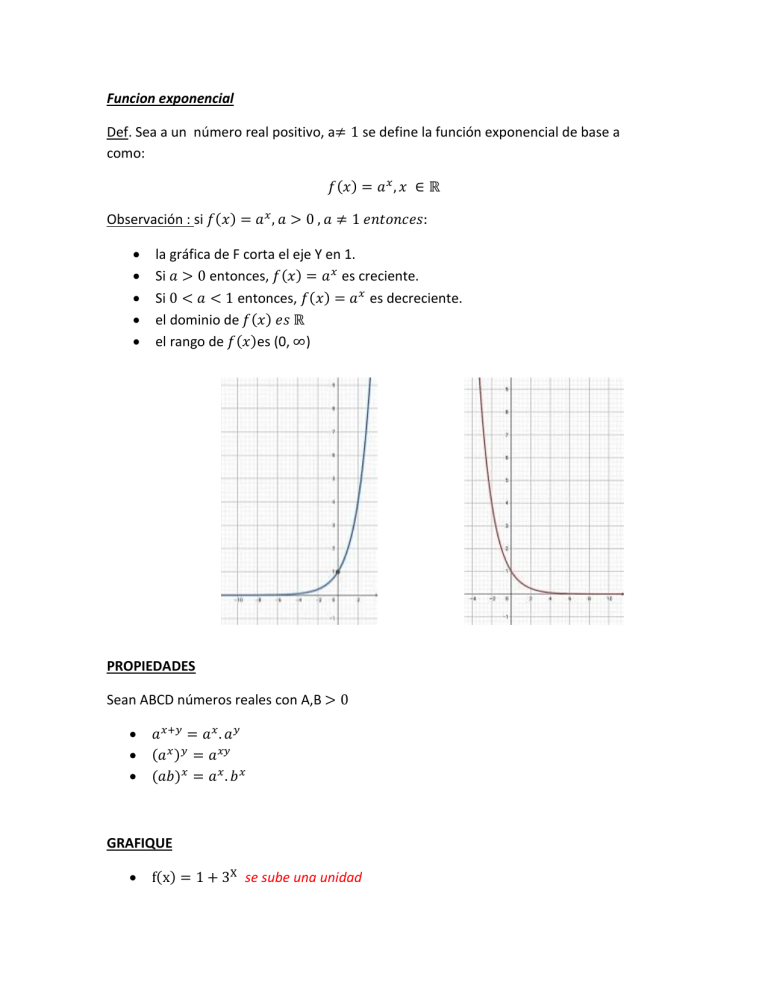
Funcion exponencial Def. Sea a un número real positivo, a≠ 1 se define la función exponencial de base a como: 𝑓(𝑥) = 𝑎 𝑥 , 𝑥 ∈ ℝ Observación : si 𝑓(𝑥) = 𝑎 𝑥 , 𝑎 > 0 , 𝑎 ≠ 1 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠: la gráfica de F corta el eje Y en 1. Si 𝑎 > 0 entonces, 𝑓(𝑥) = 𝑎 𝑥 es creciente. Si 0 < 𝑎 < 1 entonces, 𝑓(𝑥) = 𝑎 𝑥 es decreciente. el dominio de 𝑓(𝑥) 𝑒𝑠 ℝ el rango de 𝑓(𝑥)es (0, ∞) PROPIEDADES Sean ABCD números reales con A,B > 0 𝑎 𝑥+𝑦 = 𝑎 𝑥 . 𝑎 𝑦 (𝑎 𝑥 )𝑦 = 𝑎 𝑥𝑦 (𝑎𝑏)𝑥 = 𝑎 𝑥 . 𝑏 𝑥 GRAFIQUE f(x) = 1 + 3X se sube una unidad 𝑔(𝑥) = −2𝑥 se refleja ℎ(𝑥) = 2𝑥−1 una unidad a la derecha 𝑘(𝑥) = 3𝑥+2 − 3 baja tres unidades y corre dos unidades a la izquierda