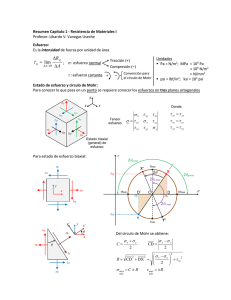
UNIVERSIDAD NACIONAL DE INGENIERIA Facultad de Ingeniería Civil ESFUERZO EN UNA MASA DE SUELO Dr. ZENON AGUILAR BARDALES CENTRO PERUANO JAPONÉS DE INVESTIGACIONES SÍSMICAS Y MITIGACIÓN DE DESASTRES - CISMID Problemas de Deformaciones Planas Típicos. Terraplén Muro de Contención z z Y Y X z X Y X Cimentación Corrida F Esfuerzo Esfuerzo Deformación (a) Esfuerzo F Deformación (c) Esfuerzo Deformación (b) Esfuerzo F R Deformación (d) F = Significa en la Falla R = Significa Valor Residual Deformación (e) Relaciones esfuerzo-deformación de materiales ideales a) elástico, b) plástico rígido, c) elastoplástico, d) elastoplástico con ablandamiento, e) relación esfuerzo-deformación típica con un material real. Superficie del terreno Tu Th Nh Nu (b) Elemento A (a) ( c) Diagramas para ilustrar la definición de esfuerzo. a) Perfil del terreno. b) y c) Fuerzas sobre el elemento A. Nivel del terreno Nivel freático Z X X Area A Nivel del terreno Nivel freático Z ZW W X X Area A Z Z y ZX XZ Z Xy y yX X y Z 1 X y a) 2 3 X b) a) Estado general de esfuerzos en un elemento de suelo, b) esfuerzos principales a Selecciones de las partículas a N Ty Huecos (poros) Tx y X Punto de contacto entre partículas situadas por encima y debajo del plano de la seccion. Definición de los esfuerzos en un sistema de partículas Concepto de Esfuerzos Efectivos H HA Agua de Poro a Partícula Sólida a Area de Corte Transversal = Ā Consideración del esfuerzo efectivo para una columna de suelo saturado sin infiltración Concepto de Esfuerzos Efectivos a1 P1 a2 P2 a3 P a4 P4 Area3 de Corte Transversal = Ā Fuerzas que actúan en los puntos de contacto de las partículas de suelo en el nivel del punto A. Distribución de Esfuerzos en una Masa de Suelo h H1 h*z H2 A Z C H2 B Entrada Válvula (abierta) Estrato de suelo en un tanque con infiltración hacia arriba Distribución de Esfuerzos en una Masa de Suelo Esfuerzo Total, σ H1 H1 + z o Presión de Poros µ Esfuerzo Efectivo σ’ o H1 γW H1 γW H1 γW + z γsat (H1 +z + iz)γw o z(γ’ – iz γw) H1 + H2 H1 γW + H2 γ sat Profundidad (a) (H1 + H2 + h) γw Profundidad (b) H2 γ’ - h γw Profundidad (c) Variación del (a) esfuerzo total; (b) presión de poro y (c) esfuerzo efectivo con la profundidad en un estrato de suelo con infiltración hacia arriba. Distribución de Esfuerzos en una Masa de Suelo Entrada Q H1 h A h*z H2 Z C H2 B Salida Válvula (abierta) Estrato de suelo en un tanque con infiltración hacia abajo Distribución de Esfuerzos en una masa de suelo Esfuerzo Total, σ H1 H1 + z o Presión de Poro µ o H1 γW H1 γW H1 γW + z γsat (H1 +z - zi)γw Esfuerzo Efectivo σ’ o z(γ’ + i γw) H1 + H2 H1 γW + H2 γ sat Profundidad (a) (H1 + H2 - h) γw Profundidad (b) H2 γ’ + h γw Profundidad (c) Estrato de suelo en un tanque con infiltración hacia abajo; variación del (a) esfuerzo total; (b) presión de poros y (d) esfuerzo efectivo con la profundidad en un estrato de suelo con infiltración hacia abajo. Esfuerzos en un Medio Elástico Causados por una Carga Puntual. P r X y X y L Z ∆σ z A Z ∆σ y ∆σ x Esfuerzos causados por un Carga Puntual Boussinesq (1883) resolvió el problema de los esfuerzos “producidos en cualquier punto de un medio homogéneo, elástico e isótropo como resultado de una carga puntual aplicada sobre la superficie de un semiespacio infinitamente grande. La solución de Boussinesq para los esfuerzos normales en un punto A causado por la carga puntual P es 2 2 2 2 ⎧ ⎡ P 3x z x −y y z ⎤⎫ ∆σ x = ⎨ 5 − (1− 2µ)⎢ 2 + 3 2 ⎥⎬ 2π ⎩ L ⎣ Lr (L + z) L r ⎦⎭ Esfuerzos Normales en A causados por una Carga Puntual 2 2 2 2 ⎧ ⎡ y −x P 3y z x z ⎤⎫ ∆σ y = ⎨ 5 − (1− 2µ)⎢ 2 + 3 2 ⎥⎬ 2π ⎩ L ⎣ Lr (L + z) L r ⎦⎭ y 3Pz 3 3Pz 3 ∆σ z = = 5 2 2 5/ 2 2πL 2π (r + z ) donde: r = x2 + y2 L = x2 + y2 + z2 = r2 + z2 µ = relación de poisson Esfuerzos en un Medio Elástico Causados por una Carga Lineal Vertical de Longitud Infinita Q por metro z ∆σx X ∆σz N Esfuerzos Causados por una Carga Lineal Vertical de Longitud Infinita Los incrementos de esfuerzo en N debidos a la aplicación de una carga lineal Q por metro, son 2Q 3 z ∆σ z = 2 2 2 π (x + z ) 2Q 2 x z ∆σ x = 2 2 2 π (x + z ) 2Q 2 xz ∆τ xz = 2 2 2 π (x + z ) Esfuerzos en un Medio Elástico Causados por una Carga de Franja (ancho finito y longitud infinita) B q = carga por área unitaria r dr X-r β X z δ ∆σz A x Carga Uniformemente Distribuida Sobre una Franja Infinita Loa incrementos de esfuerzos en el punto A producidos por una presión uniforme q que actúa sobre un franja flexible infinitamente larga de ancho B, son los siguientes: ∆σ z = ∆σ x = ∆τ xz = q π q π q π [β + senβ cos(β + 2δ )] [β − senβ cos(β + 2δ )] senβsen( β + 2δ ) Isóbaras o Bulbo de Presiones Verticales Bajo una Carga Flexible de Franja q ∆σ q B 2B 2.5B = 0.9 0.7 B 0.5 0.06 2B 0.3 a Carga de Franja flexible a ∆σ q 0.08 = 0.2 3B 4B 0.1 Planta 0 5B B 2B Isóbaras o Bulbo de Presiones Verticales Bajo una Carga Flexible de Franja 0.9q 0.8q 0.6q 0.5q B 0.4q 0.3q 2B V 0.2q Bajo el centro 3B 4B V =0.1q 5B 6B 0 a) 0.2q 0.4q 0.6q 0.8q q b) Franja infinita con carga uniformemente distribuida: a) líneas de igual incremento de esfuerzo vertical total, b) incremento del esfuerzo vertical total bajo el centro Carga con Distribución Triangular sobre una Franja Infinita B q R2 R1 Z X α β ∆σV ∆σX N Carga con Distribución Triangular sobre una Franja Infinita Cuando el esfuerzo aplicado se incrementa linealmente a través del ancho de la franja, lo cual conduce a una distribución triangular, los incrementos de esfuerzo en el punto N están dados por: q ⎡x 1 ⎤ α β ∆σ v = − sen 2 ⎥⎦ π ⎢⎣ B 2 ∆σ x ∆ τ xz 2 ⎡ ⎤ 1 q x z R1 α − 1n 2 + sen 2 β ⎥ = ⎢ π ⎣B 2 B R2 ⎦ 2z ⎤ q ⎡ = 1 + cos 2 β − x⎥ ⎢ 2π ⎣ B ⎦ Carga uniformemente distribuida sobre área circular una El incremento del esfuerzo vertical total a una profundidad z bajo el centro de una área circular flexible de radio R cargada con una presión uniforme q esta dado por ⎧⎪ ⎡ ⎤ 1 ∆ σ v = q ⎨1 − ⎢ 2 ⎥ ⎪⎩ ⎣1 + ( R / z ) ⎦ 3/ 2 ⎫⎪ ⎬ ⎪⎭ Sin embargo, para puntos diferentes de los situados bajo el centro de carga, las soluciones tienen una forma extremadamente complicada (Harr, 1996) y por lo general se presentan en forma gráfica (Foster y Ahlvin, 1954 ) o en tablas (Ahlvin y Ulery, 1962). En el punto N , puede escribirse el incremento en el esfuerzo vertical total como ∆ σ v = qI σ Factor influencia l σ 0.001 0 0.004 0.002 0.006 0.01 0.04 0.02 2 0.2 0.4 0 0.5 r =0.75 R 4 4 0.8 1 1.5 3 3 0.6 r =1 R 2.5 2 5 6 5 7 Carga uniforme q 8 6 7 0.1 0.1 1.25 1 z R 0.06 r =10 R R 9 8 V 9 r V = q/ 10 Valores del factor de influencia /σ para calcular el incremento de esfuerzo vertical total ∆σv bajo un área circular uniformemente cargada. (Según Foster y Alhvin, 1954. Reimpresa con la autorización del transportation Research board). b/z= 3.0 2.0 1.9 1.6 1.4 1.2 0.50 b/z =1.0 0.9 0.40 0.8 0.7 Influence Value ‘ I ’ 0.6 b/z =0.5 0.30 0.4 0.3 0.20 0.2 a b P 0.1 0.10 Z Z =I.P b/z=0 0 0.01 2 4 6 8 0 1 Z 2 4 6 8 1 0 2 4 6 8 10 0 a/z Factores de Influence para Esfuerzos Verticales Generados por una Carga de Terraplén (Obsterberg, 1957). Isóbaras o Bulbo de Presiones Verticales Bajo un Área Cuadrada con Carga Uniforme Carga uniforme q B B 0.9q 0.8q 0.6q 0.5B 0.5B 0.4q 0.3q B B 0.2q 0.1q V a) 1.5B 1.5B 2B 2B 2.5B 2.5B V Bajo el centro =0.5q 0 0.2q 0.4q 0.6q 0.8q 0 b) a) líneas de igual incremento de esfuerzo vertical total, b) incremento del esfuerzo vertical total bajo el centro de la zapata. Incremento de Presiones Verticales Bajo un Área Rectangular con Carga Uniforme El incremento en el esfuerzo vertical debajo la esquina de un área rectangular cargada uniformemente viene dado por: ∆ σ v = qI σ Donde Iσ es función de m y n, parámetros definidos como: como B m = z L n = z Presion uniforme q 0.24 B 0.23 L Z V N =ql Nota: m y n son intercambiables V 0.18 0.25 m=3.0 m=2.4 m=2. m=1.8 m=1.6 m=1.4 0.22 m=1.2 0.21 m=1.0 0.20 m=0.9 0.19 0.18 m=0.8 m=0.7 0.17 m=0.6 0.16 Factor de influencia I m= 0.15 0.14 m=0.5 0.13 m=0.4 0.12 0.11 0.10 m=0.3 0.09 0.08 0.07 m=0.2 0.06 0.05 0.04 m=0.1 0.03 0.02 0.01 0.00 0.01 0.02 0.04 0.06 m=0.0 0.1 0.2 0.3 0.4 0.6 0.8 1 n 2 3 456 8 10 Valores del factor de influencia Iσ para calcular el incremento de esfuerzo vertical total ∆σv bajo la esquina de una área rectangular uniformemente cargada (Según Fadum, 1948) Cálculo aproximado del incremento de esfuerzo vertical Para áreas circulares o rectangulares uniformemente cargadas, puede hacerse un cálculo aproximado del incremento de esfuerzo vertical total suponiendo que la carga aplicada se distribuye dentro de un cono truncado o una pirámide truncada formados por lados con pendiente de 2 en la vertical y 1 en la Horizontal, por ejemplo, si el área cargada es un rectángulo de longitud L y ancho B, el incremento promedio en el esfuerzo vertical total a una profundidad z estará dado aproximadamente por ∆σ v qLB = ( L + z )( B + z ) Cualquier área cargada puede considerarse como un número discreto de subáreas, que distribuyen una carga puntual aplicada sobre la superficie del terreno q LxB 1 1 2 2 Z (L+z) x (B+z) Método aproximado para calcular el incremento promedio de esfuerzo vertical total bajo un área uniformemente cargada. Ejercicio Una cimentación superficial cuadrada de 2m de lado , perfectamente flexible, transmite a un depósito de suelo homogéneo e isotrópico una carga uniforme ∆q = 200 KN/m2. Comparar la distribución de los incrementos de esfuerzo vertical, (∆σv) bajo el centro de la zapata considerando una carga distribuida y una carga puntual equivalente. Estimar a partir de que profundidad los errores entre estas distribuciones son inferiores a 0.1∆q. a) Carga uniformemente distribuida B A B A 2m 1m C D D C q =200 kn/m2 4 veces Utilizando el Ábaco de Fadum Esquina Centro Z (m) O (m,n) - - (KN/m ) (KN/m ) 200 200 2 2 0.25 4 0,247 49,4 197,6 0.50 2 0,233 46,6 186,4 1.00 1 0,177 35,4 141,6 1.50 0.67 0.125 , 25,0 100,0 2.00 0.50 0,086 17,2 2.50 0.40 0,062 3.00 0.33 0,046 9,2 36,8 3.50 0.29 0,037 7,4 29,6 4.00 0.25 0,027 5,4 21,6 12,4 68,8 49,6 Carga puntual Expresión de Boussinesq 3P ∆σ v = 3 2πz P = 2 x 2 x 200 = 800kΝ Z(m) V (KN/M2) 0,25 0,50 1,00 1,50 2,00 2,50 3,00 3,50 4,00 6.111,5 1.527,9 382,0 169,3 95,5 61,1 42,4 31,2 23,9 Comparación entre las dos distribuciones de ∆σv A partir de Z>2,20m → error absoluto (∆`σv-∆σ) /Dq < 0.1 0 50 100 200 150 1 2 2,2 3 4 z(m) V CARGA DISTRIBUIDA V CARGA PUNTUAL (kN/m ) 2 V ESTADO DE ESFUERZOS EN UNA MASA DE SUELO CÍRCULO DE MOHR Z A Tzx T 0 Txz X X Txz X Txz c Tzx Z a) Resultantes de esfuerzos sobre ab B Tzx Z b) A 3 T Dirección de REPRESENTACIÓN DE ESFUERZOS MEDIANTE EL CÍRCULO DE MOHR 1 C B 3 Dirección de (a) T A ( Coordenados 1 2 1 ,T ) 3 2 Circulo de Mohr 1 + 2 3 (b) a) estado de esfuerzos en un punto. b) Diagrama de Mohr para el estado de esfuerzos en un punto. Representación de los esfuerzos mediante el círculo de Mohr. σ θ = σ 1 cos θ + σ 3 sen θ = 2 2 σ1 + σ 3 + σ1 − σ 3 2 2 σ1 − σ 3 τ θ = (σ 1 − σ 3 ) senθ cos θ = sen 2θ 2 cos 2θ El esfuerzo tangencial máximo en un punto, τmax es siempre igual a (σ1-σ3)/2; es decir, el esfuerzo tangencial máximo equivale al radio del círculo de Mohr. Este esfuerzo tangencial máximo se produce en planos que forman ± 45° con la dirección del esfuerzo principal mayor. Ejemplo 2kg/cm 2 B 300 4kg/cm 2 4kg/cm 2 B 2kg/cm 2 Se pide calcular los esfuerzos sobre el plano B-B. 1. 2. 3. 4. 5. 6. Se representa los puntos (4,0) y (2,0). Se dibuja el círculo, utilizando estos puntos para definir el diámetro. Se traza la línea AA’ por el punto (2,0), paralela al plano sobre el cual actúa el esfuerzo (2,0). La intersección de A’A’ con el círculo Mohr en el punto (4,0) es el polo. Se traza la línea B’B’ por Op, paralela a BB. Se leen las coordenadas del punto X donde B’B’ corta al círculo de Mohr. C´ 1 OOpp B´ B’ A´ A’ A´ 0 X -1 1 2 2 B´ B’ 3 C´ 44 σ = 2.5 kg/cm2 Sobre BB τ = -0.87 kg/cm2 2.5 kg/cm 2 Respuesta 4 kg/cm 2 0.87 2 kg/cm2 Otra solución. Los pasos 1 y 2 igual que antes. 3. Traza´por el punto (4.0) la línea C’C’ paralela al plano sobre el que actúa el esfuerzo (4.0). C’C’ es vertical. 4. C’C’ corta al círculo de Mohr solamente en (4.0) de forma que este punto es el polo Op. Los pasos 5 y 6 análogos al caso anterior. Solución por medio de las ecuaciones σ 1 = 4kg / cm2σ 3 = 2kg / cm2θ = 120° 4+2 4−2 σθ = + cos 240° = 3 − cos 60° = 2.5kg / cm2 2 2 4−2 τθ = sen240° = −sen60° = −0.866kg / cm2 2 (preguntas para el alumno. ¿Por qué es θ =120°? ¿El resultado habria sido diferente si θ = 300°?) DIAGRAMAS p-q En muchos problemas conviene representar, sobre un diagrama único, muchos estados de esfuerzos para una determinada muestra del suelo. En otros problemas se representa en un diagrama de este tipo el estado de esfuerzos de muchas muestras diferentes. En tales casos resulta muy pesado trazar los círculos de Mohr, e incluso mas difícil ver lo que se ha representado en el diagrama después de dibujar todos los círculos . Otro método para dibujar el estado de esfuerzos puede ser adoptar un punto representativo de los esfuerzos cuyas coordenadas son p= σ1 + σ 3 q=± 2 σ1 − σ 3 2 + si σ1 forma un ángulo igual o menor de ± 45° con la vertical - si σ1 forma un ángulo menor de ± 45° con la horizontal En la mayoría de los casos en los que se utiliza la representación puntual, los esfuerzos principales actúan sobre planos verticales y horizontales. En este caso, la ecuación se reduce a p= συ + σ h 2 ,q = συ − σ h 2 Este método equivale a representar un punto único de un circulo de Mohr: el punto mas alto si q es positivo o el mas bajo si q es negativo. Numéricamente, q equivale a la mitad del esfuerzo desviador. Conociendo los valores de p y q para un cierto estado de esfuerzos, se posee toda la información necesaria para dibujar el círculo de Mohr correspondiente. Sin embargo, el empleo de un diagrama p-q no exime de utilizar el círculo de Mohr para determinar la magnitud de los esfuerzos principales a partir de un determinado estado de esfuerzos.