NORMAL PARAMETRICA2020

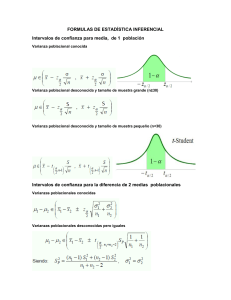
TEMA 1 . DISTRIBUCIONES CONTINUAS.
TECNICAS CUANTITATIVAS II
DISTRIBUCION NORMAL
La distribución Normal o de Gauss ajusta gran cantidad de variables no solo económicas y
sociológicas, esta versatilidad tiene su apoyo en el Teorema Central del Límite, de manera que siempre
que un determinado efecto sea producido por un gran número de causas independientes, la
distribución será aproximadamente normal. Es la más importante y más utilizada. Diremos que una
variable aleatoria
sigue una distribución Normal de parámetro
media poblacional y de
varianza poblacional
, la media está comprendida
y su varianza
. Además
su función de densidad es :
CARACTERISTICAS
 FUNCION DISTRIBUCION
no integramos su función de densidad para obtener su función
de distribución. Tendremos que utilizar la variable tipificada
. El proceso consiste en
restarle a una variable la media y dividirlo entre su desviación típica . Se buscaría el valor
en la tabla de probabilidad.






1.
2.
3.
1
Su función de densidad
es continua en toda la recta real.
es simétrica respecto a y tiene un máximo cuando x=
Tiene como asíntota horizontal el eje de abscisas, crece cuando
y decrece cuando
Sus características estocásticas son
de parámetros poblacionales
desconocidos.
Para valores concretos de sus parámetros
tenemos la normal tipificada
REPRODUCTIVIDAD: Consiste en combinar linealmente un conjunto de variables aleatorias
normales, independientes e idénticamente distribuidas. Obteniendo una nueva distribución con
dicha combinación normal.
Sea
, , ......
cada una de las variables tiene su media y su varianza. Y la nueva
combinación surge de sumar su medias poblacionales y sumar sus varianzas poblacionales al
cuadrado.
+ + .....
+ +
obteniendo una nueva normal
;
donde es una constante.
.
+
+
+
+
L.
@ ACADEMIAGAMARRA, CAMINO DE RONDA 89
685109330
©ANTONIO_QUERO