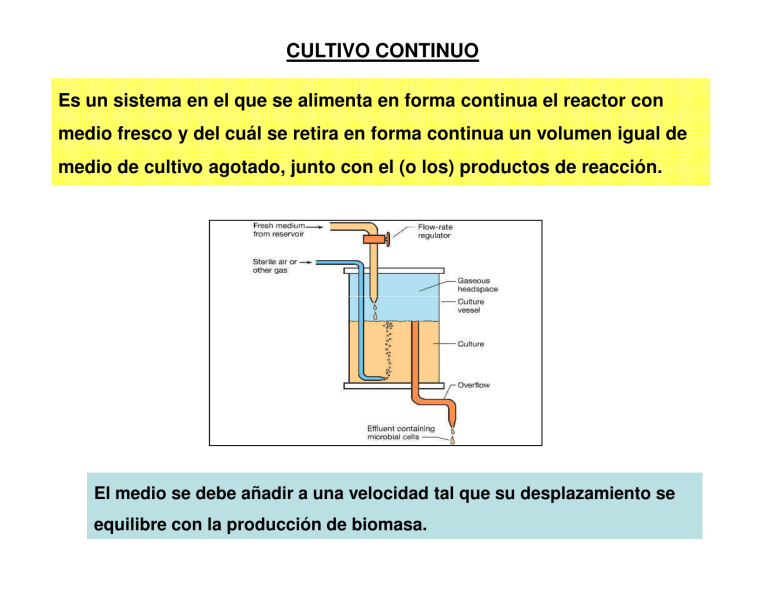
CULTIVO CONTINUO Es un sistema en el que se alimenta en forma continua el reactor con medio fresco y del cuál se retira en forma continua un volumen igual de medio de cultivo agotado, junto con el (o los) productos de reacción. El medio se debe añadir a una velocidad tal que su desplazamiento se equilibre con la producción de biomasa. µ Zona cultivo restricto µm S ~ kS µ < µm El cultivo continuo opera con bajas concentraciones de nutriente limitante, es decir en la zona de cultivos restrictos (recordar Monod). Las células adaptan su velocidad de crecimiento a la concentración del sustrato limitante (s). Antes de iniciar un cultivo continuo, se debe realizar previamente un cultivo batch para tener una cierta concentración de microorganismos. Luego se comienza a alimentar con medio fresco a un caudal F y por un rebalse se mantiene V constante. Los microorganismos dentro del biorreactor se están multiplicando, esto compensa las “pérdidas” debida a los microorganismos que son arrastrados fuera del biorreactor por el caudal de salida. Parámetros de operación característicos de c. continuos: La velocidad de dilución: D (h-1) El tiempo de retención: tR D= F V 1 tR = D El valor de D corresponde a las veces que se renueva el volumen del biorreactor por unidad de tiempo. Ej D=0,25 h-1 indica que en una hora se renovó un 25 % del volumen de cultivo. Balance de materia en el reactor F1 Ci1 F2 Ci Ci, V velocidad Veloc. Veloc. Veloc. Veloc. = − + − acumulació n Entrada Salida Form . Cons . d (VCi ) = F1 ⋅ Ci1 − F2 ⋅ Ci + V ⋅ r fi − V ⋅ rci dt (ec.1) A partir de esta ecuación general, se pueden plantear balances para biomasa, sustrato y producto. 1. Balance de biomasa d(X ) V ⋅ = 0 − F ⋅ X + V ⋅ rx − 0 dt En estado estacionario (ee) y dividiendo por V: − F ⋅ X + ⋅r x = 0 V En un cultivo continuo se considera que se alcanza el estado estacionario (ee) cuando han pasado por lo menos 4-5 tR . Teniendo en cuenta que rx = µ.x, se obtiene: µ ⋅ X = D ⋅ X Por lo tanto: µ=D La velocidad específica de crecimiento se puede controlar ajustando la velocidad de dilución (D) o sea variando el caudal F. Recordando la ec. de Monod: Despejando ) µm ⋅ S ) =D µ= ks + S ~ S ) D ⋅ ks S= µm − D O sea que en un c. continuo se controla la velocidad de crecimiento (µ) a través de la cantidad de sustrato que le suministramos (D). La concentración de s debe estar en el orden de ks (zona de cultivos restrictos). Las células adaptan su velocidad de crecimiento a la concentración del sustrato limitante (s). 2. Balance de Sustrato Aplicando el balance a un componente S: dS = F1 S R − F2 S + 0 − Vrs V dt F1 = F2 = F Dividiendo por V e igualando a 0 la ecuación anterior (ee) se obtiene: rs = D ⋅ (S R − S ) (ec.2) Donde: SR = concentración del sust. limitante en la alimentación (reservorio). S = concentración de sust. limitante en el reactor, en estado estacionario. Determinación de la concentración de biomasa en el reactor Recordando ec. Pirt: rX rS = + ms ⋅ X YX′ / S Reemplazando en la ec.2, se obtiene: D ⋅ (S R − S ) = rx ~ + ms ⋅ X YX′ / S En estado estacionario µ = D ) Despejando X (ec. 3) ) ) D ⋅ SR − S X = Y x′/ s ⋅ D + m s ⋅ Y x′/ s ( ) ) µ⋅X ~ D ⋅ (S R − S ) = + ms ⋅ X YX′ / S ) D⋅ X ~ ( ) D ⋅ SR − S = + ms ⋅ X Y X′ / S Y`x/s , ms, SR = constantes. X = f (D) se puede variar a voluntad. El tiempo desaparece como variable (ee). Si el mantenimiento fuese despreciable (ms=0) Recordando la ec. de Monod: ) µm ⋅ S ) =D µ= ks + S ~ S ) ) X = Yx / s ⋅ S R − S ( ) (ec. 4) Despejando ~ S ) D ⋅ ks S= µm − D (ec. 5) = f (D) Esta ec. indica que al variar D, varío S y la célula responde al nuevo D pero indirectamente. El D lo que hace es modificar S y este modifica el µ. Reemplazando en la ec. 4 se obtiene (ec. 6) ) D ⋅ ks X = Yx / s ⋅ S R − µm − D ) X = f ( D y de SR) Curva de S, X en función de D ) D ⋅ ks X = Yx / s ⋅ S R − µm − D Si ms = 0 1,2 2,5 X (ms= 0) 1,0 (ec. 6) 2,0 (ec. 3) 0,8 1,5 0,6 1,0 glucosa (g/l) X (biomasa) g/l X no tiende a 0 cuando D tiende a 0. (ec. 6) ) D ⋅ ks S= µm − D (ec. 5) 0,4 X 0,2 0,5 0,0 0,0 0,0 0,2 0,4 0,6 -1 D (h ) ) ) D ⋅ SR − S ′ X = Yx / s ⋅ D + ms ⋅ Yx′/ s ( ) (ec. 3) 0,8 1,0 µmax = 1.0 h-1 Y´x/s = 0,5 gX /gS ms = 0,05 gS/gX h Ks = 5 mg/l S0 = 2,0 g/l ) Cuando D → 0 ⇒ X → 0 A bajos valores de µ (D), la FCE se consume principalmente para mantenimiento (ec. Pirt) por lo tanto disminuye el rendimiento. Recordando la ecuación de Pirt………. Dividiendo la ecuación de Pirt por rx y sabiendo que los rendimientos se pueden expresar como cociente de velocidades : rs rx = + m Y x′ / s s ⋅ X 1 Yx / s ms 1 = + Y x′ / s µ ms es un valor constante. Pero el rendimiento experimental baja a medida que µ baja porque la proporción de sustrato que se usa para mantenimiento es mayor. Pirt desarrollo esta ecuación para explicar porque en un cultivo continuo, a medida que el microorganismo crecía mas lento, el rendimiento experimental bajaba. Wash out A valores altos de D Al aumentar D, x disminuye lentamente tendiendo a cero y S aumenta muy lentamente. A D altas, el organismo no puede crecer lo suficientemente rápido como para compensar la velocidad con la que son arrastrados por la corriente de salida y se produce el “lavado” del cultivo. 2,5 1,2 X (ms= 0) 2,0 0,8 1,5 0,6 1,0 0,4 X 0,2 0,5 0,0 0,0 0,0 0,2 0,4 0,6 0,8 1,0 -1 D (h ) Wash out glucosa (g/l) X (biomasa) g/l 1,0 El valor de D al cual ocurre el “lavado” o “wash out” se conoce como velocidad de dilución crítica (Dc). El valor de D al cual ocurre el “lavado” o “wash out” se conoce como velocidad de dilución crítica (Dc). ) X = 0 A Dc ocurren dos cosas ~ S = SR De la ecuación de Monod el valor de Dc será: DC = µ .m ⋅ SR KS + SR Como generalmente Ks << SR, se puede hacer la siguiente aproximación: DC ≅ µ m Por lo tanto se toma como criterio de trabajo: D < µm Si se trabaja a un D > µm las células serán arrastradas por la corriente de salida a una velocidad mayor de la que son capaces de multiplicarse, produciéndose el lavado. Trazado de la curva 1. Inicio cultivo batch para tener células. 2. Cuando s es despreciable, se inicia la alimentación con un valor de D bajo (Ej. 0,02 h-1) . Si V = 1 lt ------- F = 0,02 lt/h. 3. Esperar que el sistema alcance le estado estacionario (4 - 5 tR) Ej. 4.tR = 4. 1/D = 4 / 0,02 = 200 h. 1 0 X SR (g/l 5 ) D 8 4 6 3 4 2 2 1 S 4. Medir S y X. Se tiene un punto 0 0,5 de la curva. 5. Alimentar con un D mayor (ej. 0,05) y repetir los pasos hasta llegar al valor de µm. 1,0 En un cultivo continuo se considera que se alcanza el estado estacionario (ee) cuando han pasado por lo menos 4-5 tR . 10 Continuo X 8 X (g/l) 3 6 2 4 transitorio 1 estacionario 2 s 0 0 10 tiempo 20 30 tiempo (h) inicio alimentación 40 0 50 D Sustrato limitante (g/l) Batch 4 Efecto de la variación de SR sobre x y s ) D ⋅ ks S= µm − D ) D ⋅ ks X = Yx / s ⋅ S R − µ − D m (ec. 6) La cantidad de biomasa en el reactor se controla por la ~ S • Varía en función de D ~ X •Varía en función de D • Es independiente de SR •Varía con SR SR = 14 g/l SR = 6 g/l cantidad de nutriente limitante. SR = 2 g/l Si se fija D y se aumenta SR, ~ X aumentará 3. Balance para producto Se plantea el balance para un determinado producto: V ⋅ dP = − F .P + V ⋅ r p dt Salida - formación En estado estacionario: Despejando ) rP = D ⋅ P P rp (de cinética) P= qp ⋅ X D (ec. 7) La expresión de qp depende del tipo de producto formado: A) Productos asociados al crecimiento: P = Yp ∗ x x Si qp está relacionado a µ (D) , p y x tendrán la misma forma. De igual manera D*P y D * x. P= qp = Yp/x . qp ⋅ X D µ Productos no asociados al crecimiento: Si qp es independiente de µ (D), por lo tanto p disminuirá cuando aumente D. La productividad D.P permanecerá constante . P= qp ⋅ X D Determinación de las constantes cinéticas (ks, ms) y rendimiento Medición de ks y µm En un cultivo continuo, en estado estacionario se tenía que µ = D. De la ecuación de Monod: D= µm ⋅ S Ks + S Haciendo la inversa se obtiene la ecuación linealizada de LineweaverBurk. 1 Ks 1 1 = ⋅ + D µm S µm De la representación gráfica de 1/D en función de 1/S, se pueden calcular los valores de µm y Ks a partir de la pendiente y ordenada al origen. Rendimiento en cultivo continuo Yx/s: rendimiento experimental Yx / s = ∆x biomasa formada = = (∆S )T sustrato totalconsu mido x ( SR − s ) Productividad en cultivo continuo ) Pc = D ⋅ X ) D ⋅ ks X = Yx / s ⋅ S R − µm − D (g/l.h) (ec. 6) K ⋅D ~ Pc = XD = YX / S ⋅ D ⋅ S R − s µm − D Graficando Pc en función de D, se obtiene una curva que presenta un óptimo a la productividad máxima. 1 0 X 5 8 4 6 3 4 2 SR (g/l) 2 1 S 0 0, 5 1,0 Derivando la ecuación de PC con respecto a D e igualando a cero se obtiene el Dopt que proporciona la máxima productividad: ~ d X D / dD = 0 ks Dopt. = µ m ⋅ 1 − ks + S R Por ser KS << SR; Dopt. < µm (pero muy próximo a µm). Operando el biorreactor a valores cercanos Dopt se tendrá una productividad máxima de biomasa (pero Dopt está muy cerca de Dcrit!!). A partir de las ec. para Dopt. y de X y considerando que SR >> ks , se obtiene la ec. para la productividad máxima: Pcm = Dopt ⋅ X opt ≅ µ m ⋅ Yx / s ⋅ S R La productividad de los productos será: Pc = D ⋅ P Siendo P la concentración de producto en estado estacionario (g/l). Además sabiendo que: P= qp ⋅ X D Para productos asociados al crecimiento. (ec. 7) qp = Yp/x . µ P = Yp ∗x x Si qp está relacionado a µ (D) , P y X en ee tendrán la misma forma. De igual manera D*P y D * x. Para productos no asociados al crecimiento. P= Pc = D ⋅ P qp ⋅ X D Si qp es independiente de µ (D), por lo tanto P disminuirá cuando aumente D. La productividad D.P permanecerá constante . Diferencias entre cultivo discontinuo y continuo El cultivo continuo opera bajo condiciones de estado de equilibrio (las concentraciones de todos los componentes del cultivo son constantes). El cultivo continuo opera bajo condiciones limitantes de sustratos mientras que el cultivo batch, en la fase exponencial, funciona en presencia de exceso de sustrato. La velocidad de crecimiento en el cultivo continuo está controlada por la velocidad de dilución (y por ello bajo el control del operador) y su valor es siempre menor que µm. Por el contrario, la velocidad específica de crecimiento en la fase exponencial de un cultivo batch, alcanzará el µm correspondiente a las condiciones que prevalezcan en el cultivo. Cultivo continuo se fija un valor de D = µ < µmax. De esta manera x = cte. Ventajas y desventajas del cultivo continuo Ventajas: 1. Permite seleccionar a voluntad la velocidad específica de crecimiento y mantener a la población bacteriana creciendo a una dada velocidad en forma indefinida y constante. 2. Permite examinar el efecto de cambios en los parámetros físicos o químicos sobre el crecimiento y la formación del producto a una tasa de crecimiento constante. 3. Permite la determinación de las constantes cinéticas, energía de mantenimiento y rendimientos. 4. Resulta mas productivo que el cultivo batch. 5. Se lo puede operar en forma automática para obtener una producción de calidad constante. Desventajas 1. La mayor complejidad y costo de los equipos. 2. Como el tiempo que demanda la operación de los equipos de cultivo continuo es mayor que el de los cultivos en batch, existe un mayor riesgo de contaminación y de que se produzcan mutaciones en las cepas bacterianas en estudio. 3. El crecimiento de organismos filamentosos es difícil debido a la viscosidad y naturaleza heterogénea del cultivo que evita el crecimiento en régimen permanente. Aplicación Industrial Producción de penicilina: Los metabolitos secundarios se forman cuando los microorganismos crecen a µ bajos. Por lo que se pueden producir mediante c. continuo, a bajos valores de D. La producción de penicilina es inhibida por la presencia de ciertas sustancias en el medio de cultivo (represores de la síntesis): Ej. a) El ácido fenilacético es un precursor de la molécula de penicilina pero por encima de una cierta concentración resulta tóxico para el organismo. b) Los fosfatos inorgánicos inhiben la síntesis de muchos antibióticos. Mediante el cultivo c. se alimenta el biorreactor de a poco, manteniendo muy bajas concentraciones de los componentes del medio lo que permite eliminar los efectos represores Proceso: consiste en una fermentación en continuo en dos etapas: Primer etapa: se agrega glucosa en una proporción que permita un crecimiento rápido (c. batch). Segunda etapa: se añade glucosa a una velocidad de dilución baja, manteniendo un baja tasa de crecimiento (c. continuo). Aplicación Industrial Saccharomyces cereviseae Producción de levadura de panadería El metabolismo de S cereviseae es netamente oxidativo hasta una µ (D) de 0.2-0.25 h-1. Por encima de este valor se induce alcohólica dando metabolismo la fermentación lugar mixto a un oxidativo- fermentativo. El rendimiento celular disminuye. La Trabajar en esta zona. µ < µcrit µ > µcrit producción aeróbica de etanol se denomina Efecto Crabtree CH 2O + b O 2 + a NH 3 → yx / s X + yCO 2 / S CO 2 + φ CH 2O + b O 2 + a NH 3 → yx / s X + yco 2 / s CO 2 + yp / s EtOH + φ Problema de aplicación 1. Se estudio la acumulación de PHB (polihidroxibutirato – compuesto de reserva) en un sistema continuo y se obtuvieron los siguientes datos a climitado y O2 limitado: % PHB (p/p) D (h-1) C-L O2-L 0,053 < 1,5 45 0,13 < 1,5 40 0,21 < 1,5 20 Interprete los resultados fisiológicamente: Solución: C-limitado: cuando está limitado en C, el poco carbono que tengo lo usa para producir biomasa, no para almacenar (por lo tanto poco PHB). Es decir que si tiene poco C lo usará para crecer y mantenerse, no le sobra para alamcenar (engoradar con PHB). O2 limitado (con exceso de C): en este caso tiene exceso de sustrato pero le falta O2 (para consumir todo ese sustrato) por lo que se produce: la acumulación del material de reserva. •Ejercicio: Un investigador quiere estudiar el efecto de la temperatura en la composición macromolecular de una bacteria (% RNA) y realiza un cultivo en batch. En la fase exponencial determina en % de RNA que tiene la bacteria. ¿Las variaciones que encuentra en el % de RNA pueden ser atribuidas al efecto de la temperatura?.Que alternativa habría?. Ln x T1 T2 µ1 µ2 t Conviene cultivo continuo donde D y por lo tanto µ se pueden mantener constantes. Bibliografía Crueger, W. y Crueger A. 1993. Biotecnología: Manual de microbiología industrial. Editorial Acribia, España. Capitulo 5. Doran, P.M. 1998. Principios de Ingeniería de los Bioprocesos. Editoral Acribia S.A. Zaragosa, España. Capitulo 13. Ertola R.J.; Yantorno O. y Mignone C. 1994. Microbiología Industrial. Organización de los Estados Americanos. Washington DC. Martos, M.A. 2011. Cuaderno Teórico - Unidad temática IV: Modo de operación de biorreactores. Colección Cuadernos de Cátedra - Editorial Universitaria de la Universidad Nacional de Misiones. ISBN 978-950 – 579 212 – 2. Scraag, A. 1996.Biotecnología para ingenieros: sistemas biológicos en procesos tecnológicos. Noriega Editores. Capitulo 10. Trevan M.D. y otros. 1991. Biotecnología. Principios Biológicos. Editorial Acribia. Zaragoza. Capitulo 7. Doran, P.M. 1998. Principios de Ingeniería de los Bioprocesos. Editoral Acribia S.A. Zaragosa, España. Capitulo 4: Estequiometría (pag 76) – Rendimiento. Capitulo 5: Calor de reacción. Capítulo 11: Cinetica, rendimiento, C. batch, cinetica productos, mantenimiento. Capítulo 13: C. continuo, batch alimentado, enzimas.








