Cultivo Continuo - Universidad Nacional de La Plata

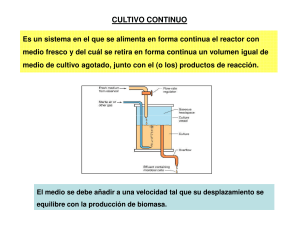
UNIVERSIDAD NACIONAL DE LA PLATA
Ingeniería Bioquímica II . 2006
Segundo cuatrimestre
CULTIVO CONTINUO
De los tres métodos usuales para el cultivo de microorganismos, batch, batch
alimentado y continuo, es este último el que ofrece mayores posibilidades de control.
Por sus características especiales permite controlar el proceso a un valor de velocidad
específica de crecimiento () prefijado de manera muy simple. Este punto es de suma
importancia ya que el comportamiento de la mayoría de los microorganismos se ve
afectado por el valor de  al que están creciendo. Por ejemplo, es común que a altos
valores (cercanos a m) formen diversos productos, siendo la naturaleza de estos
dependiente del microorganismo, mientras que a bajos valores de  no los formen.
Mediante el cultivo continuo es posible estudiar el efecto sobre el proceso de
variables como PH, temperatura, concentración de nutrientes, etc., manteniendo
constante el valor de , o bien, fijadas las anteriores, analizar el efecto de  sobre el
proceso. De este modo es posible separar los distintos efectos y obtener información
valiosa para la mejora del proceso.
Para poner en marcha un cultivo continuo, se realiza previamente un cultivo
batch y en un momento dado, normalmente cuando se agota el substrato limitante, se
comienza a alimentar el biorreactor con medio de cultivo fresco a un caudal F (Fig. 1).
F, SR
F,S,X,P
X
P
S
Fig. 1
Mediante un rebalse se logra que el volumen del cultivo permanezca constante.
El caudal de salida contendrá células, mientras que la concentración de nutrientes será
menor que en el caudal de entrada debido a que en parte fueron consumidos por los
microorganismos. Eventualmente se encontrará también algún producto(s) proveniente
de la actividad metabólica de los microorganismos.
1
UNIVERSIDAD NACIONAL DE LA PLATA
Ingeniería Bioquímica II . 2006
Segundo cuatrimestre
Una de las variables de operación fundamental en este tipo de cultivos es la
velocidad de dilución, D, la que se define como la relación entre el caudal de
alimentación, F, y el volumen de cultivo, V.
D
F
V
(1)
Teniendo en cuenta las unidades usuales de F (L. h-1) y de V (L), las de D serán de h-1.
El valor de D corresponde a las veces que se renueva el volumen del biorreactor por
unidad de tiempo, así un valor de D= 0.25 h-1 indica que en una hora se renovó un 25
% del volumen de cultivo, o bien que al cabo de 16 hs. se habrá renovado cuatro veces
el volumen de cultivo. Podría pensarse que a estas alturas prácticamente ya no quedan
microorganismos dentro del biorreactor, pero no es así; debe tenerse en cuenta que
estos se están multiplicando activamente lo cual compensa las “perdidas” debidas a los
microorganismos que son arrastrados fuera del biorreactor por el caudal de salida.
Bajo ciertas condiciones, que analizaremos mas adelante, ambos procesos se
compensan de modo tal que la concentración de microorganismos se mantiene
constante en el tiempo, es decir que se habrá alcanzado un estado estacionario. En
estas condiciones también se mantendrán constantes en el tiempo las concentraciones
de nutrientes, en particular la del substrato limitante del crecimiento, y la de
producto(s).
Balances de materia:
De acuerdo al esquema de la Fig. 1 podemos plantear los siguientes balances de
materia para la concentración de microorganismos ( X ) , de substrato ( S ) y de
producto ( P ).
V.
dX
 V .r  F . X
x
dt
V.
dS
~ V. r
 F .S  F .S
R
s
dt
V.
dP
 V .r  F .P
P
dt
(2)
(3)
(4)
Cuando se alcanza el estado estacionario, X, S y P ya no varían con el tiempo,
lo que equivale a igualar a cero las Ecs. (2), (3) y (4), de donde resulta:
r
X
~
 D. X
(5)
2
UNIVERSIDAD NACIONAL DE LA PLATA
Ingeniería Bioquímica II . 2006
Segundo cuatrimestre
~)
r  D . (S  S
S
R
~
r  D.P
P
(6)
(7)
~, P
~, S
~ representan las respectivas concentraciones en estado estacionario. La
donde X
Ec. (6) es válida para cualquier nutriente del medio de cultivo, sea el substrato
limitante o no, ya que la misma surge de un balance de materia en el que no se ha
hecho ninguna consideración con relación a la naturaleza del substrato considerado.
Lo primero que debe destacarse en este tipo de cultivo es que permite
determinar experimentalmente y de modo muy simple las velocidades de crecimiento,
consumo de substrato y de formación de producto, tal como se desprende de las Eqs.
(5), (6) y (7). Del mismo modo permite calcular los rendimientos. Por ej. Si
suponemos que S representa a la fuente de carbono y energía, el rendimiento celular se
calcula fácilmente:
~
X
Y

~)
x / s (S  S
R
(8)
De modo similar puede calcularse YP/S , o bien las velocidades específicas. Por ej. Para
qs será:
qS 
~)
rS D.(SR  S

(9)
x
x~
mientras que para la velocidad específica de crecimiento será:
~
rX
D. X

 ~ D
X
X
( 10 )
La Ec. (10) es de suma importancia pues significa que en estado estacionario es  = D,
y como D puede ser variado a voluntad por el operador (variable de operación) resulta
que el cultivo continuo permite “ imponerle” externamente a los microorganismos el
valor de  al que deben crecer.
El estado estacionario:
Hemos visto que en estado estacionario es  = D, la pregunta que surge
inmediatamente es: ¿cuanto tiempo demora el sistema en alcanzar este estado?. En
rigor, la respuesta surge de la misma definición de estado estacionario, es decir cuando
todas las variables del cultivo (X, S, P, concentración de O2 disuelto y composición de
la biomasa) no varían en el tiempo. El criterio práctico que se suele seguir es que, una
3
UNIVERSIDAD NACIONAL DE LA PLATA
Ingeniería Bioquímica II . 2006
Segundo cuatrimestre
vez fijado el valor de D, debe esperarse al menos 4.tR (ver clases teóricas) , donde tR
se conoce como tiempo de retención medio y puede demostrarse que :
tR = 1 / D
Por tanto si se fija un valor de D= 0.15 h-1, habrá que esperar 26,7 hs. para suponer que
se ha alcanzado el estado estacionario, lo que deberá ser corroborado
experimentalmente midiendo las concentraciones de X, S, P hasta observar que no
varían con el tiempo. Usualmente con 4.tR es suficiente.
4