Solución de Francisco Javier García Capitán , profesor del IES

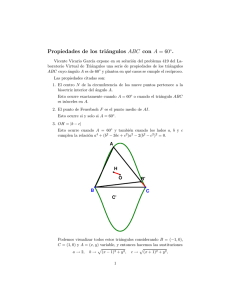
Problema 405 de triánguloscabri . Dados dos triángulos ABC y A0B 0 C 0
cumpliendo
1. los ángulos B y B 0 son iguales y la suma de los ángulos A y A0 es igual
dos rectos, o
2. los ángulos A y A0 son mayores o iguales que un recto,
probar que entre sus lados se verifica la siguiente desigualdad:
√
bb0 +
√
√
cc0 6 2aa0.
¿Cuándo se verifica la igualdad?
Propuesto por Juan Bosco Romero Márquez.
Solución de Francisco Javier Garcı́a Capitán. Supongamos primero que
los triángulos ABC y A0B 0 C 0 cumplen la primera condición. Tracemos por
C 0 la paralela a C 0B 0 cortando a la recta AB en B 00 y formando el triángulo
isósceles CB 00B.
C
C'
a
a
b
a'
b'
c
c'
B"
B'
A
B
En este triángulo tenemos
BB 00 = 2a cos B = 2a ·
a 2 + c2 − b 2
a 2 + c2 − b 2
=
,
2ac
c
B 00A = BB 00 − AB =
a 2 + c2 − b 2
a 2 − b2
−c=
.
c
c
de donde
Ahora, usando los triángulos semejantes AB 00C y AB 0C 0, tenemos que
c0
b0
a0
=
=
.
B 00A
b
a
A partir de aquı́,
0
ba
c0
b0
0
0 2
0 2
0
⇒bcc = b a − b b ⇒ bcc =
a 2 − b0 b2
2
2 =
a −b
b
a
c
⇒bcc0 = baa0 − b2 b0 ⇒ bb0 + cc0 = aa0.
Ahora usamos la
Desigualdad entre las medias aritmética y cuadrática. Si x e y son
números no negativos se cumple que
r
x+y
x2 + y 2
6
.
2
2
La igualdad se cumple si y solo si x = y.
Demostración. Basta tener en cuenta la identidad
2
x2 + y 2
x+y
1
−
6 (x − y)2.
2
2
4
Entonces será
r
r
√
√
√
√
√
bb0 + cc0
bb0 + cc0
aa0
6
=
⇒ bb0 + cc0 6 2aa0.
2
2
2
0
La igualdad se cumplirá cuando bb = cc0 . Como también es aa0 = bb0 +cc0 ,
resulta aa0 = 2bb0 . Entonces, teniendo en cuenta las relaciones B = B 0 y
A + A0 = 180◦ y usando el teorema de los senos, resulta
b
a0
b0
sen2 A
a a0
aa0
a
=
,
=
⇒
=
·
=
= 2,
sen A
sen B
sen A
sen B
sen2 B
b b0
bb0
√
es decir, sen A = 2 sen B, y por lo tanto,
a
a0 √
= 0 = 2.
b
b
Geométricamente, los puntos C y C 0 deberán estar en las circunferen√
cias de Apolonio√Γ y Γ0 formadas por los puntos tales que CB/CA = 2
y C 0 B 0/C 0A0 = 2 respectivamente. Para visualizar todas estas soluciones
situamos el punto A = A0 sobre una recta, los puntos B y B 0 también sobre
esa recta, cada uno en una de las semirrectas determinadas por A, y trazamos
las mencionadas circunferencias de Apolonio. Para cualquier punto C sobre
Γ, la recta CB 0 determina el vértice C 0 sobre la circunferencia Γ0 .
C
C'
B'
A
B
—
Supongamos ahora que A > 90◦ y A0 > 90◦ . En este caso, usaremos la
Desigualdad de Cauchy-Schwarz. Si u = (u1 , u2) y v = (v1, v2) son dos
vectores se verifica
q
q
u1 v1 + u2v2 6 u21 + u22 v12 + v22,
cumpliéndose la desigualdad si y solo si los vectores son proporcionales.
Observemos antes que si aplicamos la desigualdad entre las medias aritmética y cuadrática en un triángulo ABC con A > 90◦ tendremos
r
√
b 2 + c2
b+c
a
6
6 √ ⇒ b + c 6 2a,
2
2
2
cumpliéndose la igualdad si y solo si A = 90◦ y b = c.
√ √
√ √
Ahora, si aplicamos esta desigualdad a los vectores ( b, c) y ( b0 , c0 )
tendremos
q
q
√
√ √
√
√
√
√
√
√ √ 0 √
0
0
0
0
0
bb + cc = b b + c c 6 b + c b + c 6
2a
2a0 = 2aa0,
cumpliéndose la igualdad si y solo si los dos triángulos son rectángulos isósceles (b = c y b0 = c0 ).