Vectores - clasesalacarta

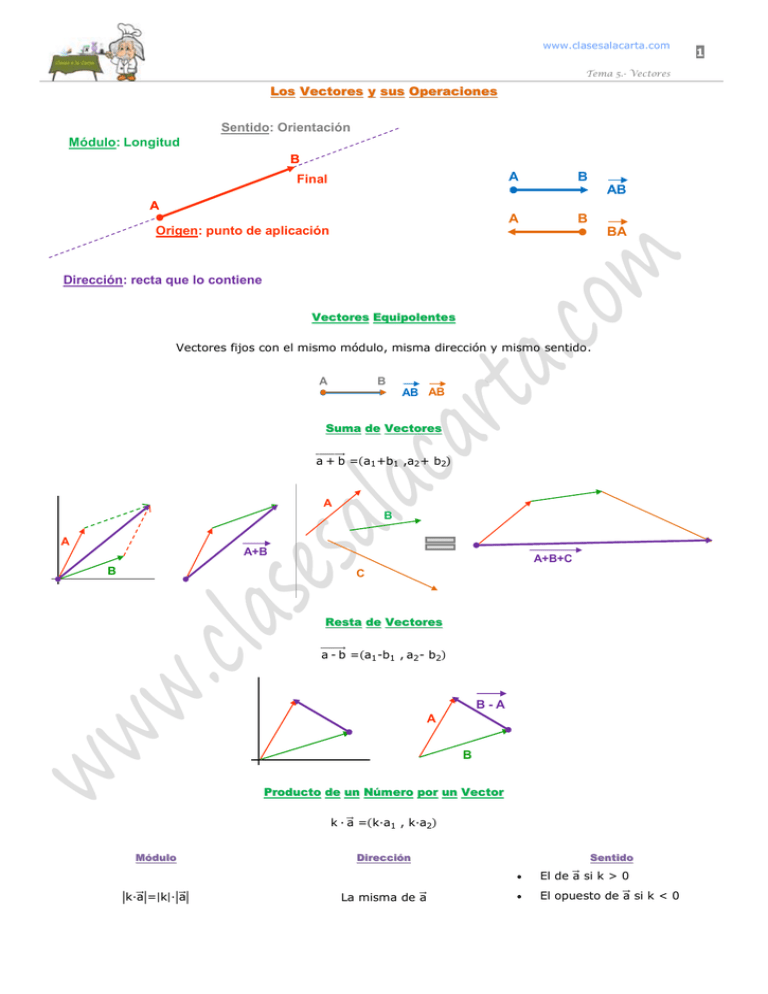
www.clasesalacarta.com
Tema 5.- Vectores
Los Vectores y sus Operaciones
Sentido: Orientación
Módulo: Longitud
B
B
A
Final
AB
A
B
A
Origen: punto de aplicación
BA
Dirección: recta que lo contiene
Vectores Equipolentes
Vectores fijos con el mismo módulo, misma dirección y mismo sentido.
B
A
AB AB
Suma de Vectores
a + b = a1 +b1 ,a2 + b2
A
B
A
A+B
B
A+B+C
C
Resta de Vectores
a - b = a1 -b1 , a2 - b2
B-A
A
B
Producto de un Número por un Vector
k · a = k·a1 , k·a2
Módulo
k·a = k · a
Dirección
La misma de a
Sentido

El de a si k > 0

El opuesto de a si k < 0
1
á
á
2
Matemáticas _ B_ 1º Bach.
Vector cero
Vector Opuesto
0·a =0
-1 · a = -a
Combinación Lineal de vectores
Dados 2 vectores a y b y 2 números k y z, el vector k·a + z·b se dice que es combinación lineal de a y b .
k·a + z·b = k a1 + z b1 , k a2 + z b2


Cualquier vector se puede poner como combinación lineal de otros dos
Esta combinación lineal es única
Coordenadas de un Vector. Base
Dos vectores a y b con distinta dirección y no nulos forman una base: cualquier vector del plano se puede poner
como combinación lineal de ellos.
Base OrtoGONAL
Base OrtoNORMAL
Vectores perpendiculares entre sí
Vectores perpendiculares entre sí y de módulo 1
Coordenadas de un Vector respecto de una base
w =a x + b y →


w (a, b)
B (x, y): base
(a, b): coordenadas de w respecto de B
Producto Escalar de un Vector
a · b= a · b · cos (a, b) = k
Propiedades
1.- El producto escalar del vector 0 por otro vector
cualquiera es el nº 0:
a=0
ó → a · b =0
b=0
2.- Si 2 vectores son
perpendiculares, su producto
escalar es 0:
a ⊥ b→ a · b = 0
3.- El producto escalar de 2 vectores es igual al
producto de uno de ellos por la proyección del otro
sobre él, con signo + o -, según si forman ángulo agudo
u obtuso. Llamando a la proyección ortogonal de a
4.- Propiedad Conmutativa:
a· b= b·a
5.- Propiedad Asociativa:
n
a· b = n·a ·b
6.- Propiedad Distributiva
a b + c = a · b+ a · c
7.- Si B x + y es una base ortogonal:
sobre b, a' :
x·y= y· x=0
a' =
a· b
b
8.- Si B x + y es una base ortonormal:
x·y= y· x=0
x·x=1
y·y=1
www.clasesalacarta.com
3
Tema 5.- Vectores
Base Ortonormal
Expresión Analítica
Si las coordenadas de los vectores a y b respecto a una base ortonormal son a (a1 , a2 ) y b (b1 , b2 ), entonces el
producto escalar a · b:
a · b= a1 ·b1 + a2·b2
Módulo de un Vector
Expresión Vectorial
Expresión Cartesiana
a = a·a
a = a21 · a22
Ángulo de 2 vectores
Expresión Vectorial
cos
a·b =
Expresión Analítica
a·b
cos
a·b =
a · b
a1 ·b1 + a2 ·b2
2
2
a21 + a22 · b1 + b2
Vector Ortogonal a Otro
Un vector ortogonal a (x, y) es (-y, x) ó (y, -x): se cambian de orden y una de signo
Vector Unitario
a a1 ,a2 → Vector Unitario
a1
a2
·
a21 + a22
a21 + a22
Coordenadas del Vector que Une 2 Puntos
A = a1 , a2
AB = b1 , b2 - a1 , a2
B = (b1 , b2 )
Condición para que 3 puntos estén Alineados
A = a1, a2
B = b1, b2
C = c1 , c2
b1 - a1
b2 - a2
=
c1 - b1
c2 - b2
Punto Medio de un Segmento
M=
a1 + b1 a2 + b2
,
2
2