valores extremos y puntos de silla

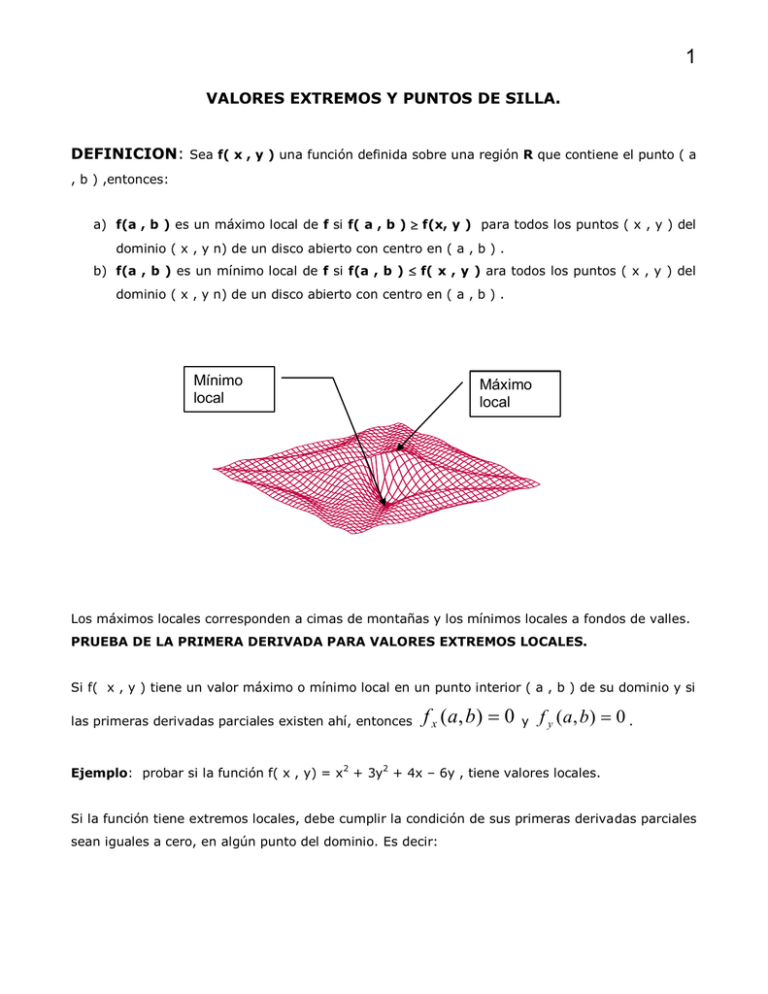
1
VALORES EXTREMOS Y PUNTOS DE SILLA.
DEFINICION: Sea f( x , y ) una función definida sobre una región R que contiene el punto ( a
, b ) ,entonces:
a) f(a , b ) es un máximo local de f si f( a , b )  f(x, y ) para todos los puntos ( x , y ) del
dominio ( x , y n) de un disco abierto con centro en ( a , b ) .
b) f(a , b ) es un mínimo local de f si f(a , b )  f( x , y ) ara todos los puntos ( x , y ) del
dominio ( x , y n) de un disco abierto con centro en ( a , b ) .
Mínimo
local
Máximo
local
Los máximos locales corresponden a cimas de montañas y los mínimos locales a fondos de valles.
PRUEBA DE LA PRIMERA DERIVADA PARA VALORES EXTREMOS LOCALES.
Si f( x , y ) tiene un valor máximo o mínimo local en un punto interior ( a , b ) de su dominio y si
las primeras derivadas parciales existen ahí, entonces
f x ( a, b)  0
y
f y (a, b)  0 .
Ejemplo: probar si la función f( x , y) = x 2 + 3y2 + 4x – 6y , tiene valores locales.
Si la función tiene extremos locales, debe cumplir la condición de sus primeras derivadas parciales
sean iguales a cero, en algún punto del dominio. Es decir:
2
f x ( a , b)  0
pero
f x ( x, y )  2 x  4
con lo que
0  2x  4
y
x  2
f y ( a, b)  0
pero
f y ( x, y )  6 y  6
con lo que
0  6y  6
y
y  1,
Es decir las primeras derivadas se hacen cero en el punto ( - 2
, 1 ), lo que nos indica que la
función tiene u extremo local en ese punto.
Ejemplo: probar si la función f( x , y) = 3x 2 + y2 + 4x – 6xy , tiene valores locales.
Si la función tiene extremos locales, debe cumplir la condición de sus primeras derivadas parciales
sean iguales a cero, en algún punto del dominio. Es decir:
f x ( a , b)  0
pero
f x ( x, y )  6 x  4  6 y
f y ( a, b)  0
pero
f y ( x, y )  2 y  6 x
Solucionando el sistema lineal:
con lo que
con lo que
3x  3 y  2

 y  3x  0
0  6x  4  6 y
0  2 y  6x
se tiene que
x
Es decir las primeras derivadas se hacen cero en el punto ( 1/3
1
3
e
y 1
, 1 ), lo que nos indica que la
función tiene un extremo local en ese punto.
DEFINICION: Un punto interior del dominio de una función f( x , y ) donde
f y ( a, b)  0
f x ( a , b)  0
y
o donde una o ambas no existan , es un punto critico de f.
DEFINICION: Una función diferenciable f( x , y ) tiene un punto de silla en un punto critico ( a ,
b ) si en todo disco abierto con centro en ( a , b ) hay puntos del dominio ( x , y ) donde
f ( x, y)  f (a, b)
correspondiente
superficie.
y puntos del dominio ( x , y ) donde
a, b, f (a, b)
f ( x, y)  f (a, b) .
El punto
sobre la superficie z = f (x , y) se llama punto de silla de la
3
Punto de
silla
Ejemplo: Sea la función f ( x , y ) = 3y2 – 2x2 , a lo largo e eje x ( puntos de la forma ( x , 0)
la función tiene el valor de f(x , y ) = – 2x2 , es decir f( x , y ) < 0; y a lo largo del eje de las y ,
la función toma valores de f( x , y) = 3y2 , es decir f( x ,y ) > 0. lue4go la función tiene un punto
de silla en el origen.
PRUEBA DE LA SEGUNDA DERIVADA PARA VALORES EXTREMOS LOCALES.
Supongamos que f ( x , y ) y sus primeras y segundas derivadas parciales son continuas en todo
disco con centro en ( a , b ) y que
f x ( a, b)  f y ( a, b)  0
, entonces
Sea el determinante formado por las segundas derivadas parciales evaluadas en el punto crítico.
D
f xx (a, b)
f yx (a, b)
f xy (a, b)
f yy (a, b)
Pero como las derivadas cruzadas son iguales:
D
f xx (a, b)
f xy (a, b)
f xy (a, b)
2
 f xx (a, b) f yy (a, b)   f xy (a, b) 
f yy (a, b)
4
Analizando el signo de la segunda derivada parcial con respecto a x y el signo del determinante,
se pueden caseificar los puntos críticos de acuerdo con el siguiente criterio.
1) f tiene un máximo local si
f xx (a, b)  0
y
D  0.
2) f tiene un mínimo local si
f xx (a, b)  0
y
D0
D0
3) f tiene un punto de silla si
4) si
D0
el criterio no decide nada y es necesario aplicar otros criterios para determinar
el comportamiento de la función.
EJEMPLO:
Encontrar
los
valores
extremos
de
la
función
f ( x, y )  3 x 3  y 2  9 x  4 y
Inicialmente se buscan las derivadas parciales.
f y ( x, y )  2 y  4
f x ( x, y )  9 x 2  9
Se iguales las primeras derivadas a cero para encontrar los puntos críticos.
f x ( x, y )  0
;
0  9x2  9
f y ( x, y )  0
;
0  2y  4
críticos son:
Con lo que
x  1
y  2 ,
Donde se obtiene
luego los posibles puntos
1,2 y  1,2
Ahora buscamos las segundas derivadas y las evaluados en los puntos encontrados:
f xx ( x, y )  18 x
Para el punto
;
f yy ( x, y )  2
f xy ( x, y )  0
1,2 se tiene que
f xx (1,2)  18 (1)  18
Ahora se evalúa
igual a cero.
;
,
f yy (1,2)  2
y
f xx (a, b) f yy (a, b)   f xy (a, b)
2
f xy (1,2)  0
para determinar si es mayor , menor o
5
f xx (1,2) f yy (1,2)   f xy (1,2)  18 * 2  0  36  0
2
Como
f xx (1,2)  0
y
f xx (a, b) f yy (a, b)   f xy (a, b)  0
2
de acuerdo al segundo
criterio de la segunda derivada, se concluye que la función tiene un mínimo local en el punto
1,2 .
f (1,2)  3(1)3  (2) 2  9(1)  4(2)  3  4  9  8  10
1,2,10 
Evaluamos las segundas derivadas en el punto  1,2 
Luego el mínimo local es el punto
f xx (1,2)  18(1)  18
Ahora se evalúa el determinante
,
f yy (1,2)  2
y
f xy (1,2)  0
f xx (a, b) f yy (a, b)   f xy (a, b)
2
para determinar si es
mayor , menor o igual a cero.
f xx (1,2) f yy (1,2)   f xy (1,2)  18 * 2  0  36  0
2
Como
f xx (a, b) f yy (a, b)   f xy (a, b)  0
2
de acuerdo al tercer criterio de la segunda
derivada, se concluye que la función tienen un punto de silla en
 1,2 .
ACTIVIDAD.
Encuentre los máximos y mínimos locales , y los puntos de silla de las siguientes funciones.
f ( x, y )  x 2  xy  y 2  3x  3 y  4
f ( x, y )  x 2  3xy  3 y 2  6 x  3 y  6
f ( x, y )  5 x 2  2 xy  2 y 2  4 x  4 y  4
6
f ( x, y )  xy  y 2  2 x  2 y  2
f ( x, y )  x 2  4 xy  y 2  6 y  2
f ( x, y )  4 x 2  6 xy  5 y 2  20 x  26 y
f ( x, y )  x3  3xy  y 3
2. resolver los siguientes problemas.
1. Una caja rectangular descansa sobre el plano xy con uno de su vértices en el origen. Hallar
el volumen máxima de la caja si su vértice opuesto al origen pertenece al plano 6x+4y+3z
= 24.
2. El beneficio que se obtiene produciendo x unidades del modelo A e y unidades del modelo
B
se
aproxima

mediante

el
P( x, y )  8 x  10 y  0.001  x 2  xy  y 2  10000
modelo:
. Determine el nivel
de producción que reporta el beneficio máximo.
3. La suma de la longitud y el perímetro de una sección de los paquetes enviados por correo
no puede exceder de 216 cm. Halle las dimensiones del paquete rectangular de mayor
volumen admitido por el correo.
4. Repetir el problema anterior si la suma de los dos perímetros de las secciones no puede
pasar de 216 cm.