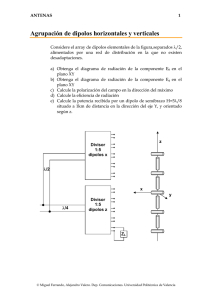
1.3 Dipolo eléctrico elemental o de Hertz.

1.3 Dipolo eléctrico elemental o de Hertz.
DIPOLO PEQUEÑO
Una buena aproximación de la distribución de corriente para antenas de alambre, cuyas longitudes son
usualmente λ/50 ≤ l ≤ λ /10, es la variación triangular de la figura siguiente.
a) Dipolo Pequeño
b) Distribución de corriente
Arreglo geométrico, del dipolo pequeño y su distribución de corriente
Matemáticamente:
z¢ ö
æ
aˆ z I 0 ç1 ÷
è l /2ø
I e ( x¢, y¢, z¢) =
z¢ ö
æ
aˆ z I 0 ç1 ÷
è l /2ø
En donde:
I 0 = cons tan te
0 £ z¢ £
-
l
2
l
£ z¢ £ 0
2
(1.3)
Siguiendo el mismo procedimiento, de la sección, anterior, el Vector Potencial de se puede escribir
empleando (1.3), como:
A( x, y, z ) =
m
4p
l/2
- jkR
é 0 æ 2 ö e - jkR
ù
æ 2 ¢ö e
¢
¢
+
dz¢ú
+
d
z
a
I
z
a
I
z
1
1
ˆz ò 0 ç
÷
÷
ê ˆz ò 0 ç
è l ø R
0
ë -l / 2 è l ø R
û
(1.4)
Debido a que la longitud total del dipolo es muy pequeña (normalmente l ≤ λ / 10 ), los
valores de r para diferentes valores de z” a lo largo de la longitud del alambre (-l/2 ≤ z’
≤ l/2), no diferentes de gran manera de r. Como consecuencia se puede aproximar R =
r, a través de la trayectoria de integración.
El máximo error de fase para (1.4), entre λ / 50 ≤ l λ/10 con R = r y l = λ/10 será:
kl 2p æ 1 öæ l ö p
=
ç ÷ç ÷ = = 0.314159654 - radianes = 180°
l è 2 øè 10 ø 10
2
Valores pequeños ocurren para otros valores. Se considera despreciable la fase de error, ya que
tiene muy poco efecto sobre las características de radiación. Así podemos realizar la integración
de (1.4), tenemos que:
l/2
- jkR
ù
m é 0 æ 2 ö e - jkR
æ 2 öe
A( x, y, z ) =
dz¢ + aˆ z ò I 0 ç1 - z¢ ÷
dz¢ú
êaˆ z ò I 0 ç1 + z¢ ÷
4p ë -l / 2 è l ø r
è l ø r
0
û
(1.4 a)
Sí hacemos:
-l / 2
- jkr
0
A1 = aˆ z
æ 2 öe
I 0 ç1 + z¢ ÷
dz¢
ò
l
r
è
ø
-l / 2
A2 = aˆ z
y
- jkr
æ 2 öe
ò0 I 0 çè1 + l z¢ ÷ø r dz¢
Reacomodando y resolviendo para A1; tenemos:
- jkr
2 e - jkr
e - jkr
æ 2 öe
dz¢ + aˆ z I 0
dz¢ = aˆ z ò I 0
A1 = aˆ z ò I 0 ç1 + z¢ ÷
r
l r
l ø r
-l / 2 è
-l / 2
0
0
0
ò z¢dz¢
-l / 2
(1.5)
= aˆ z I 0
0
0
ù
e - jkr é
e - jkr
2
¢
¢
¢
d
z
z
d
z
a
I
=
+
ê
ú ˆz 0
r ë-lò/ 2
l -lò/ 2
r
û
e - jkr
= aˆ z I 0
r
0
é 0
2æ1 2ö ù
¢
¢
z
z
+
ç
÷ ú
ê -l / 2
l è 2 ø -l / 2 úû
êë
2
éæ æ l ö ö 2 æ
2ö l æ l ö ù
e - jkr é l l ù
êçç 0 - ç - ÷ ÷÷ + ç 0 - ÷ ç - ÷ ú = aˆ z I 0
l ø 2 è 2 ø ûú
r êë 2 4 úû
ëêè è 2 ø ø l è
I 0le - jkr
e - jkr é l l ù
e - jkr é l ù
- = aˆ z I 0
A2 = aˆ z I 0
= aˆ z
r êë 2 4 úû
r êë 4 úû
4r
(1.6)
Ahora resolviendo para A2 :
- jkr
e - jkr
2 e - jkr
æ 2 öe
dz¢ - aˆ z I 0
dz¢ = aˆ z ò I 0
A2 = aˆ z ò I 0 ç1 - z¢ ÷
r
l r
è l ø r
0
0
l/2
l/2
l/2
ò z¢dz¢
0
l/2
l/2
l/2
ù
e - jkr é
2
e - jkr é l / 2 2 æ 1 2 ö ù
= aˆ z I 0
ê z¢ 0 - ç z¢ ÷ ú
ê dz¢ - ò z¢dz¢ú = aˆ z I 0
r ë ò0
l 0
r êë
l è 2 ø0 ûú
û
= aˆ z I 0
e - jkr
r
2
éæ l
ü öù
e - jkr
ö 2 æç 1 ì l
÷
0
0
a
I
=
ˆ
÷
êç
í
ý ÷ú
z 0
r
ø l çè 2 î 4
êëè 2
þ øúû
A2 = aˆ z
I 0le - jkr
él l ù
a
=
ˆ
z
êë 2 4 úû
4r
I 0le - jkr
4r
Sustituyendo (1.4 b ) y (1.7 ) en (1.4 a ), Tenemos que:
A( x, y, z ) =
m
4p
l/2
- jkR
ù
é 0 æ 2 ö e - jkR
æ 2 ¢ö e
¢
¢
dz¢ú
d
z
a
I
z
a
I
z
+
+
1
1
ˆz ò 0 ç
÷
÷
ê ˆz ò 0 ç
è l ø r
0
û
ë -l / 2 è l ø r
A( x, y, z ) =
m
4p
é I 0le - jkR
ù m é I 0le - jkr ù
I 0le - jkR
¢
d
z
a
a
+
ˆ
ˆ
z
ê z 4r
ú = 4p ê 2r ú aˆ z
4r
ë
û
ë
û
(1.7)
A( x, y, z ) Az aˆ z =
m é I 0le - jkr ù
aˆ
2p êë 4r úû
z
(1.8)
La ec. (1.8 ) es exactamente la mitad que la del dipolo infinitesimal, dada por ( 1.4 a ), La
función potencial dada por (1.8 ), obtiene mas presión cuando aproximamos kr → ∞ , es decir
en la región de campo lejano.
La transformación entre los componentes rectangulares y esféricas se da, en forma de matriz,
por:
Ar
Aθ
senθ cosφ
=
Aφ
senθ cosφ cosφ
Ax
cos θ cosφ cosθ senφ -senθ
Ay
-senφ
Az
cosφ
0
(1.9)
Para este problema Ax = Ay = 0, usando (1.8) se reduce a:
Ar = Az cos(q ) =
mI 0le - jkr
cos(q )
8pr
mI 0le - jkr
Aq = - Az sen(q ) = sen(q )
8pr
(1.10 a)
(1.10 b)
Af = 0
(1.10 c)
Usando la simetría del problema (sin variaciones en φ), puede expresarse en coordenadas
esféricas y escribirse en forma simplificada como:
H = aˆq
1 é¶
(rAq ) - ¶( Ar ) ùú
ê
mr ë ¶r
¶q û
(1.11)
Sustituyendo (1.10 a)(1.10 c) o (1.11) lo reduce a:
H r = Hq = 0
Hr = j
kI0lsen(q ) é
1 ù - jkr
1+
e
ê
8pr
jkr úû
ë
(1.12 a)
(1.12 b)
Las componentes de los campos de e y H son validos en cualquier punto, excepto en la propia fuente y
se grafican en la Fig. ariba mostrada b, sobre la superficie de una esfera de radio r.
Puesto que la función potencial para la distribución de corriente triangular es la mitad de la corriente,
para la distribución constante (uniforma) del dipolo infinitesimal, podemos utilizar los pasos, de las
ecuaciones de manera similar y escribir los campos de radiados por un dipolo pequeño en el campo
lejano.
kI0le - jkr
Eq @ jh
sen(q )
8pr
Er @ Ef H r = Hq = 0
kI0le - jkr
Hq @ jh
sen(q )
8pr
(1.13)
Kr >> 1
(1.14)
(1.15)
La razón de Eθ a Hφ es igual a:
Z onda =
Eq
@h
Hf
(1.16)