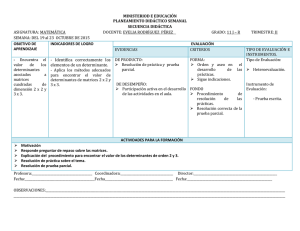
2. MATRICES Y DETERMINANTES

Matrices y Determinantes
2. MATRICES Y DETERMINANTES
SUMARIO:
INTRODUCCIÓN
OBJETIVOS
INTRODUCCIÓN TEÓRICA
1.- Matrices.
2.- Operaciones con Matrices.
3.- Equivalencia de Matrices. Transformaciones Elementales de
Matrices.
4.- Cálculo de la Matriz Inversa.
5.- Determinantes.
6.- Desarrollo de un Determinante.
7.- Propiedades de los Determinantes.
8.- Expresión de la Matriz Inversa .
PROBLEMAS RESUELTOS.
BIBLIOGRAFÍA
MATEMÁTICAS I
35
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
INTRODUCCIÓN
En este punto del temario surge un dilema para el profesor. Si se
persigue una rigurosidad matemática habría que comenzar este segundo
bloque definiendo la estructura de Espacio Vectorial, para a continuación y
como ejemplo, definir las Matrices, pasando posteriormente a las
aplicaciones lineales, los sistemas de ecuaciones y finalmente como ejemplo
de aplicación multilineal, dar los determinantes.
Sin embargo en un curso de Álgebra lineal dentro de la formación de
un Ingeniero Técnico, creemos que se debe ser más flexible en el orden de
los temas atendiendo fundamentalmente al criterio de que al alumno lo que
le interesa es el manejo práctico que de toda esta herramienta puede realizar.
Es por esto que, siendo fieles a la evolución del Álgebra, comenzamos el
tema incentivándolos mediante un ejemplo en el que halla que resolver un
sistema de ecuaciones y a continuación les exponemos toda la matemática
necesaria que les facilitará dicha resolución: las matrices y los determinantes,
para finalmente atacar con esta herramienta cualquier sistema de ecuaciones
que se les presente. Este orden nos permite mostrarles los espacios
vectoriales dotados de una gran cantidad de elementos matemáticos que nos
evitarán teorizar en demasía y avanzar con fluidez en los siguientes temas.
36
MATEMÁTICAS I
Matrices y Determinantes
OBJETIVOS
•
Realizar con soltura las distintas operaciones con matrices.
•
Comprobar que las matrices cuadradas de orden n tienen una
estructura de anillo.
•
Conocer las posibles operaciones elementales, e identificarlas con
el producto por la correspondiente matriz elemental.
•
Comprender su significado y calcular con precisión el rango de una
matriz.
•
Manejar el método de Gauss para hallar una matriz escalonada
equivalente.
•
Determinar subconjuntos notables de matrices cuadradas como
diagonales, matrices de traza nula, triangulares de cada tipo,
simétricas, antisimétricas, hermíticas, antihermíticas, etc.
•
Calcular, si es posible, como producto de matrices elementales, la
inversa de una matriz cuadrada.
•
Comprender el sentido de las propiedades de los determinantes,
cuyo fin es calcularlos con mayor comodidad que siguiendo la
definición.
•
Conocer y practicar con soltura el cálculo de un determinante por
los diferentes métodos y elegir la estrategia más adecuada en cada
caso.
•
Calcular con soltura el rango de una matriz empleando
determinantes.
MATEMÁTICAS I
37
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
•
Decidir si una matriz tiene inversa, o no, a través de su propio
determinante. Cuando exista, calcular la inversa mediante
determinantes.
38
MATEMÁTICAS I
Matrices y Determinantes
INTRODUCCION TEORICA
1. MATRICES
Una matriz A de orden m × n es un conjunto de m ⋅ n elementos
pertenecientes a un cuerpo K , ordenados en m filas y en n columnas.
A=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
a11
a12 " a1n ⎞⎟
a21
a22 " a2 n ⎟⎟
⎟
#
an1
#
%
⎟
⎟
⎟
⎟
⎟
nn ⎠
#
an 2 " a
= ⎛⎜⎝ ai j ⎞⎟⎠ donde i = 1,...m , j = 1,..., n .
Nosotros consideraremos que K es el cuerpo \ o ^ .
Simbolizaremos una matriz por una letra mayúscula A o por :
⎛
⎜
⎝
ai j ⎞⎟⎠i =1,2,..., m ,
j =1, 2,..., n
o de forma más sencilla por ⎛⎜⎝ ai j ⎞⎟⎠ (el subíndice i nos indica la fila en la
cual se encuentra el elemento, el j la columna).
1.1. Tipos particulares de Matrices
Si m = 1 la matriz A se llama matriz fila.
Si n = 1 la matriz A se llama matriz columna.
Si m ≠ n la matriz A se llama matriz rectangular
Si m = n la matriz A se llama matriz cuadrada y se dice de orden n .
NOTACIONES
El conjunto de matrices de orden m × n cuyos elementos toman valores
del cuerpo K se simboliza por M m×n ( K ) .
MATEMÁTICAS I
39
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
Si K = \ , se simplifica la notación por M (m, n) o M m×n .
El conjunto de matrices cuadradas de orden n se simboliza por M n ( K ) .
Si K = \ , utiliza la notación M n o M n×n .
1.2. Definición de Matriz Nula
Matriz nula O n×n es aquella en que todos sus elementos son 0 , es decir,
ai j = 0 , ∀i = 1, 2,..., m , ∀j = 1, 2,..., n . Cualquiera que sea el orden de las
matrices con las que se trabaje, siempre es posible definir su matriz nula.
1.3. Definición de Diagonal Principal
Si A es una matriz cuadrada de orden n la diagonal principal de A es los
elementos de la forma aii , ∀i = 1, 2,...n .
1.4. Definición de Traza
Traza de una matriz cuadrada A es la suma de los elementos de la
diagonal principal:
Traza( A) = Tr ( A) = a11 + a22 + " + ann .
2. OPERACIONES CON MATRICES
2.1. Igualdad
Dos matrices A y B del mismo orden m × n son iguales si y sólo los
elementos situados en las mismas posiciones en ambas matrices coinciden,
es decir, si: ai j = bi j ,
40
MATEMÁTICAS I
Matrices y Determinantes
∀i = 1, 2,..., m , ∀j = 1, 2,...n .
2.2. Suma de matrices
Dadas dos matrices A y B del mismo orden m × n se define la matriz
suma C = A + B, como la matriz de orden m × n que resulta de sumar
entre sí los elementos que ocupan las mismas posiciones en ambas matrices,
es decir:
ci j = ai j + bi j , ∀i = 1, 2,...m, ∀j = 1, 2,..., n .
2.3. Producto de una matriz por un número
Dada una matriz A de orden m × n y dado un elemento λ ∈ K , la matriz
B = λ A (producto de la matriz A por el elemento del cuerpo λ ) es la
matriz de orden m × n que resulta de multiplicar todos los elementos de A
por λ , esto es:
bi j = λ ai j , ∀i = 1, 2,..., m , ∀j = 1, 2,..., n .
2.4. Producto de matrices
Dadas dos matrices A de orden m × n y B , de orden n × p , su matriz
producto C = A ⋅ B es una matriz de orden m × p tal que:
n
ci j = ∑ ai k bk j = ai1b1 j + ai 2b2 j + " + ai nbn j
,
∀i = 1, 2,..., m ,
k =1
∀j = 1, 2,..., p .
IMPORTANTE: Para que se puedan multiplicar dos matrices, el número
de columnas de la primera debe ser igual al número de filas de la segunda.
El producto de matrices no es conmutativo .
MATEMÁTICAS I
41
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
2.5. Trasposición de matrices
Dada una matriz A de orden m × n se define su matriz traspuesta, que se
simboliza por At como la matriz que resulta de intercambiar en A sus filas
por sus columnas, esto es:
(ait j ) , donde i = 1,...m , j = 1,..., n y con ait j = a j i .
El orden de la matriz traspuesta es n × m .
Las principales propiedades de la trasposición de matrices son:
( A + B)
t
( A⋅ B)
= B t ⋅ At .
t
= At + B t
2.6. Tipos de Matrices Cuadradas
Una matriz A, cuadrada de orden n se dice que es:
Diagonal, si ai j = 0 , si i ≠ j .
Escalar, si es diagonal y ai i = a , ∀i = 1, 2,..., n .
Identidad, si es escalar y ai i = 1 , ∀i = 1, 2,..., n . Se denota por I .
Triangular superior, si ai j = 0 , ∀i > j .
Triangular inferior, si ai j = 0 , ∀i < j .
Regular o invertible, si existe su inversa (trabajando con el producto de
matrices).
A la matriz inversa se la denota por A−1 y verifica:
A ⋅ A−1 = A−1 ⋅ A = I .
Singular, si no tiene inversa.
Simétrica, si At = A .
42
MATEMÁTICAS I
Matrices y Determinantes
Antisimétrica, si A = − A , (también se denomina hemisimétrica).
t
Idempotente, si A2 = A .
Involutiva, si A2 = I .
Ortogonal, si At = A−1 .
3. EQUIVALENCIA DE MATRICES. TRANSFORMACIONES ELEMENTALES
DE MATRICES
Las transformaciones elementales de fila más importantes son:
La permutación de las filas i y j , que denotaremos por Fi j .
El producto de la fila i por una constante k ≠ 0 , denotada por Fi ( k ) .
Sumar a la fila i la j multiplicada por k , denotada por Fi j (k ) .
Análogamente las transformaciones elementales de columnas son Ci j ,
Ci ( k ) , y Ci j (k ) .
3.1. Matriz Elemental
Matriz elemental es toda matriz que resulta de aplicar una transformación
elemental a la matriz identidad. Fi denotará una matriz elemental general
de tipo fila y C j denotará una matriz elemental general de tipo columna.
Las distintas matrices elementales son:
1.- Fi j y Ci j que resultan de intercambiar en la matriz identidad I n×n las
filas i y j , en el caso de Fij , o las columnas i y j , en el caso de Ci j . Por
lo tanto,
MATEMÁTICAS I
43
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
si I n×n
⎛1 0 " " " " 0⎞
⎜
⎟
#⎟
⎜0 % %
⎜# % 1 %
#⎟
⎜
⎟
=⎜#
% 1 %
#⎟
⎜#
% 1 % #⎟
⎜
⎟
% % 0⎟
⎜#
⎜0 " " " " 0 1⎟
⎝
⎠
se tiene que al intercambiar las filas (o las columnas) i y j resulta:
i
j
⎛1
⎞
⎜
⎟
#
⎜ % #
⎟i
⎜ " 0 " 1 " ⎟
⎜
⎟
Fi j = Ci j = ⎜
#
#
⎟j
⎜ " 1 " 0 " ⎟
⎜
⎟
#
# % ⎟
⎜
⎜
1 ⎟⎠
⎝
2.- Fi (k ) y Ci (k ) que resultan de multiplicar en la matriz identidad I n×n
la fila i por el escalar k , en el caso de Fi (k ), o la columna i por el escalar
k , en el caso de Ci (k ).
i
⎛1
⎞
⎜
⎟
%
#
⎜
⎟
⎜
⎟
1 #
⎜
⎟
Fi (k ) = Ci (k ) = ⎜" " " k " " " ⎟ i
⎜
⎟
# 1
⎜
⎟
#
%
⎜
⎟
⎜
1 ⎟⎠
⎝
44
MATEMÁTICAS I
Matrices y Determinantes
3.- Fi j (k ) y Ci j (k ) que resultan de sumar en la matriz identidad I n×n a la
fila i
la j multiplicada por el escalar k , en el caso de Fij (k ), o a la
columna i la j multiplicada por el escalar k , en el caso de Ci j .
⎛1
⎞
⎜
⎟
⎜ %
⎟i
⎜
1 " k " "⎟
⎜
⎟
Fi j (k ) = ⎜
% #
⎟j
⎜
1 " "⎟
⎜
⎟
%
⎜
⎟
⎜
1 ⎟⎠
⎝
i
j
⎛1
⎞
⎜
⎟
%
⎜
⎟
⎜" " 1
⎟
⎜
⎟
Ci j (k ) = ⎜
# %
⎟
⎜" " k " 1
⎟
⎜
⎟
#
# % ⎟
⎜
⎜
1 ⎟⎠
#
#
⎝
NOTA: La matriz que se obtiene al realizar una transformación elemental
en la matriz A de orden n × m por filas (columnas) coincide con la matriz
obtenida al multiplicar por la izquerda (derecha) la matriz A por la matriz
elemental correspondiente.
En la matriz
A = ⎛⎜⎝ ai j ⎞⎟⎠i =1,2,..., n
j =1, 2,..., m
se pueden obtener las siguientes
transformaciones, siendo i < j .
MATEMÁTICAS I
45
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜⎜
⎝
a11 " a1i " a1 j " a1m ⎞⎟
⎟
" " " " " " " ⎟⎟
⎟
a j1 " a j i " a j j " a j m ⎟⎟
⎟
Fi j A = " " " " " " " ⎟⎟
ai1 " aii " ai j " ai m ⎟⎟
⎟
" " " " " " " ⎟⎟
⎟
an1 " ani " an j " an m ⎟⎟⎠⎟
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜⎜⎝
a11 " a1 j " a1i " a1m ⎞⎟
⎟
" " " " " " " ⎟⎟
ai1 " ai j
⎟
" ai i
" ai m ⎟⎟
⎟
ACi j = " " " " " " " ⎟⎟
a j1 " a j j " a j i " a j m ⎟⎟
⎟
" " " " " " " ⎟⎟
⎟
an1 " an j " ani " an m ⎟⎟⎟⎠
Fi j (k ) A =
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜⎜⎝
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜⎜⎝
a11
"
a1i
"
a1 j
"
a1m
"
"
"
"
"
"
"
ai1 + k a j1 " aii + k a j i " ai j + k a j j " ai m + ka
"
a j1
"
"
"
"
"
"
"
a ji
"
an1
"
ani
a11 "
a1i + k a1 j
" "
"
ai1 "
aii + k ai j
" a1 j
"
"
"
"
aj j
"
"
"
ajm
"
"
an j
"
an m
" a1m ⎞⎟
" " "
" ai j
⎞
⎟
⎟
⎟
⎟
⎟
⎟
jm ⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟⎟⎠
⎟
⎟
⎟
⎟
⎟
im ⎟
⎟
⎟
⎟
⎟
jm ⎟
⎟
⎟
⎟
⎟
⎟
n m ⎟⎟⎠
"
" a
"
" " " "
ACi j = " "
a j1 " a j i + k a j j " a j j " a
46
" "
"
" " "
"
an1 " ani + k an j " an j " a
MATEMÁTICAS I
Matrices y Determinantes
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜⎜
⎝
a11
"
a1i
"
"
"
"
"
a1 j
"
a1m
"
k ai1 " k aii " k ai j " k ai m
Fi (k ) A = "
a j1
"
an1
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜⎜⎝
"
"
"
"
"
"
"
"
"
a ji
"
aj j
"
ajm
"
"
"
ani
"
"
"
an j
"
"
"
an m
a11 " k a1i
" " "
" a1 j
" "
ai1 " k ai i "
Ci (k ) A = " " "
a j1 " k a ji
"
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟⎟
⎠
" a1m ⎞⎟
⎟
" " ⎟⎟
⎟
ai j "
ai m ⎟⎟
"
"
"
⎟
⎟
⎟
⎟
jm ⎟
⎟
⎟
⎟
⎟
⎟
n m ⎟⎟⎠
" aj j " a
" " " " " " "
an1 " k ani " an j " a
3.2. Matrices equivalentes
Dos las matrices A y B , se dice que son equivalentes si una se puede
obtener de la otra a través de transformaciones elementales.
Por tanto, si A y B ∈ M n×m son equivalentes, se tiene que:
B = Fr " F2 F1 AC1C2 " Cs
siendo F1 , F2 , …, Fr
matrices elementales que representan las
transformaciones aplicadas a las filas de A y C1 , C2 , …, Cs las
transformaciones aplicadas a las columnas de A , para obtener la matriz B .
Entonces si P = Fr " F2 F1 y Q = C1C2 " Cs se tiene A y B son
equivalentes si y sólo si existen P y Q regulares tales que B = PAQ ; P y
Q se denominan matrices de paso.
MATEMÁTICAS I
47
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
4. CÁLCULO DE LA MATRIZ INVERSA
La matriz
A
(cuadrada) tiene inversa si y sólo si mediante
transformaciones elementales sólo en sus filas o sólo en sus columnas, se
llega a la matriz identidad.
Si
Ef
y
Ec
son las operaciones elementales que aplicadas,
respectivamente, a las filas o a las columnas de A conducen a la identidad,
es decir: E f ( A) = Fr ⋅…⋅ F1 ⋅ A = I y E c ( A) = Cs ⋅…⋅ C1 ⋅ A = I , entonces se
tiene que:
A−1 = E f (I) (las operaciones elementales se han realizado en las filas en
A ), o
A−1 = E c (I) (las operaciones elementales se han realizado en las columnas
de A )
4.1. Matrices Semejantes
Dos matrices A y B cuadradas de orden n son semejantes si existe una
matriz P regular tal que B = PAP −1 .
5. DETERMINANTES
Si llamamos M n ( K ) al anillo de todas las matrices cuadradas sobre el
cuerpo K , podemos definir el determinante como una aplicación de
M n ( K ) en K :
det : M n ( K ) ----K
A ---- det( A)
48
MATEMÁTICAS I
Matrices y Determinantes
⎛
⎜
⎝
⎞
i j ⎟⎠
Si A = a
entonces su determinante se puede simbolizar de las
siguientes maneras:
det( A)
det ⎡⎣ a1 , a 2 ,…, a n ⎤⎦ ,
( por a i se simboliza a la columna de lugar i de la
matriz A )
A=
a11
a12 " a1n
a21
"
a22 " a2 n
" " "
an1
an 2 " ann
Esta aplicación tiene que verificar las siguientes propiedades:
det ⎡⎣ a1 , a 2 ,…, a ′i + a ′′i ,…, a n ⎤⎦ = det ⎡⎣ a1 , a 2 ,…, a ′i ,…, a n ⎤⎦ +
+ det ⎡⎣ a1 , a 2 ,…, a ′′i ,…, a n ⎤⎦
det ⎡⎣ a1 , a 2 ,…, λ a i ,…, a n ⎤⎦ = λ det ⎡⎣ a1 , a 2 ,…, a i ,…, a n ⎤⎦ , (λ ∈ K ).
det ⎡⎣ a1 , a 2 ,…, u,…, u…, a n ⎤⎦ = 0
det I = 1
En esta definición se pueden sustituir las columnas a i de A por sus filas;
más adelante se verá que de ambos modos se llega a un mismo resultado.
Se llama determinante de orden
n al determinante de una matriz de
tamaño n × n .
5.1. Menor Complementario
Sea
A
una matriz cuadrada,
A ∈ M n (K ) .
Llamamos menor
complementario del elemento ai j al determinante de la matriz que resulta
MATEMÁTICAS I
49
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
de suprimir la fila i y la columna j de la matriz A . Lo denotamos por
αi j .
5.2. Adjunto de un Menor Complementario
El adjunto del menor complementario α i j se denota por Ai j y viene dado
por:
Ai j = ( −1) α i j .
i+ j
6. DESARROLLO DE UN DETERMINANTE
El determinante de una matriz cuadrada de orden n , A = ⎛⎜⎝ ai j ⎞⎟⎠ se puede
obtener como suma de los productos de los elementos de una de sus filas (o
de una de sus columnas) por sus correspondientes adjuntos.
7. PROPIEDADES DE LOS DETERMINANTES
Sea A ∈ M n ( K ) , se cumple que:
Si todos los elementos de una fila (o una columna) de A son 0 entonces
A = 0.
Si multiplicamos por k ∈ K todos los elementos de una fila (o una
columna) de A , entonces el determinante de A queda multiplicado por k .
Si se permutan dos filas (o dos columnas) de A entre sí , entonces el
determinante de A cambia de signo.
Si A tiene dos filas (o dos columnas) iguales, entonces A = 0 .
Si A tiene una fila (o una columna) proporcional a otra, entonces A = 0 .
50
MATEMÁTICAS I
Matrices y Determinantes
Si a una de las filas ( o a una de las columnas ) de A le sumamos una
combinación lineal de las restantes, el determinante de la matriz no varía.
A ⋅ B = A ⋅ B , A, B ∈ M n×n
Si A es una matriz invertible, entonces A ≠ 0.
7.1. Menor de orden p
Sea A = ⎛⎜⎝ ai j ⎞⎟⎠ una matriz de orden m × n cualquiera, y elegidas las p filas
i1 , i2 ,…, i p de A , (con p ≤ m y p ≤ n ), se llama menor de orden p de A ,
que determinan las p filas y las p columnas elegidas, al determinante de la
submatriz de A de tamaño p × p , que forman los elementos situados en
los cruces de las filas y columnas elegidas; esto es, al determinante:
ai1 j1
M=
" " ai1 j p
" " " "
" " " "
ai p j1 " " ai p j p
7.2. Rango de una matriz
Se dice que p es el rango de una matriz A ∈ M m×n ( K ) , si A tiene algún
menor de orden p no nulo y todos los menores de A de orden mayor que
p son nulos; o sea, p es el mayor de los órdenes de los menores no nulos
de A . Se denota por Rang ( A) = p .
MATEMÁTICAS I
51
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
8. EXPRESIÓN DE LA MATRIZ INVERSA
Sea A = ⎛⎜⎝ ai j ⎞⎟⎠ una matriz cuadrada, de tamaño n × n . Se llama matriz
adjunta de A , a la matriz A∗ = ⎛⎜⎝ ai∗j ⎞⎟⎠ , con ai∗j = Aij = ( −1) α i j de tamaño
i+ j
n × n . Se verifica que si A es una matriz regular, es decir si A ≠ 0 ,
entonces:
⎛ a11
⎜ A
⎜ a12∗
=⎜ A
⎜
⎜ #
⎜⎜ a1∗n
⎝ A
∗
−1
A =
52
( A∗ )t
A
∗
a21
A
∗
a22
A
#
a2∗ n
A
⎞
⎟
an∗ 2 ⎟
# A ⎟
⎟
# # ⎟
a∗
# An n ⎟⎟
⎠
#
an∗1
A
MATEMÁTICAS I
Matrices y Determinantes
PROBLEMAS RESUELTOS
1.- Sean las matrices
D∈M 4 x4
con D regular
A, B ∈ M 4 x 3
y
C ∈M 3x4
y la matriz
(determinante distinto de 0).
De las
siguientes operaciones hay una que no es posible realizar, ¿cuál es?
a) ( A + B) C D −1
b) D −1 ( A + B) C
c) B C D 3
d)
D C ( A + B)
SOLUCIÓN:
Las operaciones del apartado a) sí se pueden realizar porque las matrices
A y B tienen la misma dimensión 4 x 3 , por lo tanto A + B ∈ M 4 x 3 ,
además el número de columnas de esta matriz coincide con el de filas de C ,
por lo que también se puede realizar ( A + B) C ∈ M 4 x 4 , por último, como
D es regular, podemos asegurar que existe D −1 ∈ M 4 x 4 , y de nuevo, por
coincidir
las
dimensiones,
podemos
efectuar
el
siguiente
producto: [ ( A + B) C ] D −1 .
Las operaciones del apartado b) también se pueden realizar. Como D es
regular, podemos asegurar que existe D −1 ∈ M 4 x 4 , y ya hemos visto también
que existe la matriz
A + B ∈ M 4 x 3 , como el número de columnas de
D −1 que es 4, coincide con el número de filas de A + B , podemos realizar el
producto D −1 ( A + B)∈ M 4 x 3 , de nuevo el número de columnas de esta
nueva matriz, que es 3, coincide con el número de filas de C , por lo que
podemos realizar el siguiente producto sin ningún problema D −1 ( A + B) C .
MATEMÁTICAS I
53
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
Las operaciones del apartado c) son perfectamente viables. La matriz B
tiene 3 columnas y la matriz C 3 filas, por lo que podemos realizar
B C ∈ M 4 x 4 , por otro lado D 3 es una matriz 4 x 4 , por lo que es posible
realizar BCD 3 ∈ M 4 x 4 .
La operación de este apartado no es factible, pues la matriz D tiene 4
columnas que no coincide con el número de filas de la matriz C , que es 3,
por lo tanto, no es posible realizar DC .
2.- Sean las matrices A ∈ M 4 x 3 (\); B ∈ M 4 x 3 (\); C ∈ M 3 x 4 (\);
D ∈ M 4 x 4(\);
¿Cual de las siguientes operaciones no se puede realizar?
a) ( A + B ).C .D
b) D.( A + B).C
c) B.C.D3
d) D.C .( A + B).
SOLUCIÓN:
a) Falso, si se puede realizar.
( 4x3 + 4x3 )(3x4)(4x4) → ( 4x3)(3x4)(4x4) → ( 4x4)(4x4) → (4x4)
b) Falso, si se puede realizar.
(4x4)( 4x3 + 4x3 )(3x4) ⎯→ ( 4x4)(4x3)(3x4) → ( 4x3)(3x4) → (4x4)
c) Falso, si se puede realizar.
(4x3)(3x4)(4x4)(4x4)(4x4) → ( 4x4)(4x4)(4x4)(4x4) → ( 4x4)
d) Verdadera.
(4x4)(3x4)( 4x3 + 4x3 ) , los ordenes, (4x4) y (3x4) no son compatibles
para la multiplicación.
3.- Dada una matriz A cualquiera, razonar la veracidad o
falsedad de los siguientes enunciados:
54
MATEMÁTICAS I
Matrices y Determinantes
a) El producto AA está definido cualquiera que sea el tamaño de
t
A.
b) El producto A( At A) está definido cualquiera que sea el tamaño
de A.
c) El producto A( At A)t está definido cualquiera que sea el tamaño
de A.
d) Para que el producto AAt esté definido es necesario que A sea
cuadrada.
SOLUCIÓN:
a) Verdadero.
A ∈ M nxm ⇒ At ∈ M mxn , por lo tanto sí es posible realizar
AAt ∈ M nxn .
b) Verdadero.
A ∈ M nxm ⇒ At ∈ M mxn , por lo tanto, podemos hacer At A ∈ M mxm y como
A ∈ M nxm entonces podemos realizar A( At A) ∈ M nxm .
c) Verdadero.
A ∈ M nxm ⇒ At ∈ M mxn , por lo tanto, podemos hacer
At A ∈ M mxm ⇒ ( At A)t ∈ M mxm entonces podemos realizar
A( At A)t ∈ M nxm .
d) Falso.
Para que AAt esté definido no es necesario que A sea una matriz
cuadrada.
MATEMÁTICAS I
55
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
⎛ 2 3 4⎞
Sea A = ⎜
⎟ ∈ M 2 x 3 (no es cuadrada) ⇒
⎝1 0 1⎠
⎛2 1⎞
⎜
⎟
⇒ At = ⎜ 3 0 ⎟ ∈ M 3 x 2
⎜4 1⎟
⎝
⎠
y
⎛ 29 6 ⎞
AAt = ⎜
⎟.
⎝ 6 2⎠
4.- Calcular el valor de los siguientes determinantes:
1 1
2 3
a)
4 9
8 27
1
1
d)
1
1
x
y
z
t
1 1
1 5
1 25
1 125
y
z
t
x
1 0
1 2
b)
x −1
y z
0
0
3
3
0
0
0
4
1
0
c)
−5
0
2
3
8
2
0
0
4
0
3
5
4
7
x+ y
x+ y
x+ y
x+ y
SOLUCIÓN:
a)
1 1
2 3
4 9
8 27
1 1
a
1 5 ( des por 1 F )
=
1 25
1 125
3
1
5
= 9
1
25 − 4 1
27 1 125
2 1
5
2
3
5
2
3
1
25 + 4
9
25 − 4
9
1=
8 1 125
8 27 125
8 27 1
= −240 + 120 + 180 − 12 = 48
b)
56
MATEMÁTICAS I
Matrices y Determinantes
1 0
1 2
x −1
y z
0
0
3
3
0
0
= 1⋅ 2 ⋅ 3 ⋅ 4 = 24 , al tratarse de una matriz triangular, su
0
4
determinante es el producto de los elementos de la diagonal principal.
c)
1
0
−5
0
2
3
8
2
0
0
4
0
3
1 2 3
a
5 ( des . por 3 C )
= 4 0 3 5 = 4 ⋅11 = 44
4
0 2 7
7
d)
1
1
1
1
x
y
z
t
y
z
t
x
x+ y
1
1
x+ y
= ( x + y)
1
x+ y
1
x+ y
x
y
z
t
y
z
t
x
1
1 ( hay dos colum iguales )
=
1
1
= ( x + y ) ⋅ 0 = 0.
5.- Dada una matriz cuadrada de orden 11 y λ ∈ \ , calcular el
valor del determinante: −λ A
SOLUCIÓN:
Al multiplicar la matriz A por −λ lo que se está haciendo es multiplicar
cada uno de los elementos de la matriz por −λ .
Al calcular el
determinante de una matriz, si toda una fila (o una columna) de la matriz
está multiplicada por el mismo número, éste se puede sacar fuera del
determinante (propiedad 2 de las numeradas como propiedades de los
determinantes).
MATEMÁTICAS I
En nuestro caso tenemos las 11 filas de la matriz A
57
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
multiplicadas por −λ , por lo tanto al calcular −λ A podemos sacar 11
veces el −λ fuera de la matriz, con lo que nos queda lo siguiente:
−λ a11
−λ a12 " " −λ a1n
−λ a21
−λ a22 " " −λ a2 n
−λ A =
#
%
#
%
−λ an1
a11
a21
= −λ #
#
an1
#
=
#
−λ an 2 " " −λ ann
−λ a12 " " −λ a1n
−λ a22 " " −λ a2 n
%
# =
%
#
−λ an 2 " " −λ ann
a11
a12
−λ a13 " −λ a1n
a21
= ( −λ ) #
#
a22
−λ a23 " −λ a2 n
%
=
%
an1
an 2
−λ an 3 " −λ ann
a11
a12
a13 " a1n
a21
= " = ( −λ ) #
#
a22
a23 " a2 n
%
# = (−λ )11 A .
% #
an1
an 2
" " ann
2
11
6.- Calcular los valores de x que hacen cero el determinante de la
matriz
58
MATEMÁTICAS I
Matrices y Determinantes
⎛x a b
⎜
x x d
A=⎜
⎜x x x
⎜⎜ x x x
⎝
c⎞
⎟
e⎟
con a, b, c, d , e ∈ \ .
f⎟
⎟
x ⎟⎠
SOLUCIÓN:
b
c
F21 ( −1)
F31 ( −1)
x
x
x d
e
F41 ( −1)
0
x−a d −b
e−c
x
x
x
f
0
x−a
x−b
f −c
x
x
x
x
0
x−a
x−b
x−c
x a
A=
F32 ( −1)
F42 ( −1)
=
F43 ( −1)
=
=
a
b
c
=
x
a
b
0 x−a d −b
0
0
x−d
0
0
x−d
c
e−c
=
f −e
x−e
x
a
b
0 x−a d −b
0
0
x−d
0
0
0
c
e−c
= x( x − a)( x − d )( x − f ) = 0 ⇐⇒
f −e
x− f
⇐⇒ x = 0 o x = a o x = d o x = f
7.- Dada una matriz diagonal se tiene que es invertible:
a) Siempre
b) Nunca
c) Si la traza es no nula.
d) Si todos los elementos de la diagonal principal son no nulos.
SOLUCIÓN:
a) Falsa.
MATEMÁTICAS I
59
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
⎛1 0 0⎞
⎜
⎟
Como contraejemplo, sea la siguiente matriz A = ⎜ 0 0 0 ⎟ se trata de
⎜0 0 1⎟
⎝
⎠
una matriz diagonal, sin embargo no es invertible porque A = 0 .
b) Falsa.
⎛1 0 0⎞
⎜
⎟
Como contraejemplo, sea la siguiente matriz A = ⎜ 0 1 0 ⎟ se trata de
⎜0 0 1⎟
⎝
⎠
una matriz diagonal y es invertible, su inversa es ella misma
⎛1 0 0⎞
⎜
⎟
A = ⎜0 1 0⎟ .
⎜0 0 1⎟
⎝
⎠
−1
c) Falsa.
⎛1 0 0⎞
Nos vale el mismo contraejemplo del apartado a). Sea A = ⎜⎜ 0 0 0 ⎟⎟ su
⎜0 0 1⎟
⎝
⎠
traza será la suma de los elementos de la diagonal principal, por lo que
Traza ( A) = 1 + 1 = 2 , sin embargo hemos visto que no es invertible.
d) Verdadera.
Sabemos que el determinante de una matriz diagonal es el producto de
todos los elementos de la diagonal principal, por lo que si ninguno de ellos
es nulo, el determinante será distinto de cero por lo que la matriz es
invertible.
60
MATEMÁTICAS I
Matrices y Determinantes
⎛
⎜ 11
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜⎜⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
nn ⎟⎠
a
0
0 " "
a22 0
0
0
A= #
% % %
# ⇒ A = a11 .a22…ann ≠ 0, ya que
#
% %
0
" "
0
0
a
aii ≠ 0 ∀i . ⇒ ∃A−1 .
8.- Si A ∈ M n es idempotente ( A2 = A) y además es ortogonal
( A−1 = At ) , calcular cuál es el valor de su determinante.
SOLUCIÓN:
Por ser A−1 A = I , tenemos que A−1 A = I = 1 . Luego, tenemos que:
−1
1= A A = A
−1
( A = At )
( A−1 = At )
A
=
t
A A
=
A = A
2
( A2 = A )
2
=
A
9.- Sea A ∈ M nxn (C ) una matriz cuadrada antisimétrica de orden
impar y con entradas complejas, ¿cuánto vale su determinante?
SOLUCIÓN:
Conocemos dos propiedades de los determinantes que se verifican para
cualquier matriz A ∈ M nxn (C ) :
1) A = At
2) λ A = λ n A
Una matriz se dice que es antisimétrica si A = − At , lo cual nos garantiza
una tercera propiedad para nuestra matriz:
3) A = − At
y ademas n es impar:
MATEMÁTICAS I
61
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
4) (−1) n = −1
Utilizando todo esto tenemos en nuestra matriz:
A (3) = − At (1) = − A = (−1) A (2) = (−1) n A (4) = − A ⇒
⇒ A =− A ⇒2 A =0⇒ A =0
⎛ n
⎛λ 1 ⎞
⎜λ
n
10.- Si A = ⎜
⎟ , λ ∈ R, demostrar que A = ⎜⎜⎜
⎝0 λ⎠
⎝ 0
nλ n −1 ⎞⎟
λn
⎟
⎟⎟
⎠
.
SOLUCIÓN:
Lo comprobaremos por inducción sobre n.
Veamos
que
es
cierto
para
λ 2 2λ ⎞⎟ ⎛⎜ λ 2 2λ 2−1 ⎞⎟
⎟ =⎜
⎟,
n = 2, A =
0 λ 2 ⎟⎟⎠ ⎜⎜⎝ 0
λ 2 ⎟⎟⎠
2
⎛
⎜
⎜
⎜⎜
⎝
supongamoslo cierto para n − 1 y veamos que que ocurre para n.
λ n −1 (n−1)λ n −1 ⎞⎟ ⎛ λ 1 ⎞
⎟
⎟=
n −1
⎟⎟ ⎜
⎜ 0
0
λ
λ
⎝
⎠
⎝
⎠
⎛
⎜
An = An −1 ⋅ A = ⎜⎜
⎛
⎜
λn
⎜
⎝
0
= ⎜⎜
λ n −1 +(n−1)λ n −1λ ⎞⎟ ⎛⎜ λ n
⎟ =⎜
⎟⎟
⎜⎜
λn
⎠
⎝ 0
nλ n −1 ⎞⎟
λn
⎟
⎟⎟
⎠
11.- Si A ∈ M nxn ( R) tiene exactamente n − 1 filas (o columnas) no
nulas, razona la veracidad o falsedad de:
a) Rang ( A) = n − 1 ;
b) Rang ( A) = 1 ;
c) Det ( A) = 1 ;
d) Det ( A) = 0
SOLUCIÓN:
a) Falsa.
Si A tiene exactamente (n − 1) filas o columnas no nulas, esto no me
indica que sean linealmente independientes, podría suceder que las (n − 1)
62
MATEMÁTICAS I
Matrices y Determinantes
líneas que no son nulas sean todas iguales con lo que se tendría que el rango
de A es como máximo 1, o que sólo dos sean linealmente independientes,
con lo que Rang ( A) = 2 ......
Como ejemplo valga el siguiente:
⎛1 1 0 ⎞
⎜
⎟
A = ⎜ 1 1 0 ⎟ ∈ M 3 x 3 , esta matriz tiene exactamente
⎜1 1 0 ⎟
⎝
⎠
n − 1 = 3 − 1 = 2 columnas no nulas, sin embargo su rango no es 2 , ya que
⎛1 1 0 ⎞
⎛1 0 0 ⎞
⎜
⎟
⎜
⎟
Rang ( A) = Rang ⎜ 1 1 0 ⎟ = Rang ⎜1 0 0 ⎟ = 1
⎜1 1 0 ⎟
⎜1 0 0 ⎟
⎝
⎠
⎝
⎠
O sea también la siguiente matriz:
⎛1
⎜
1
B=⎜
⎜1
⎜⎜
⎝1
1
1
1
1
0
1
1
1
0⎞
⎟
0⎟
∈ M 4 x 4 , esta matriz tiene exactamente (n − 1) =
0⎟
⎟
0 ⎟⎠
= 4 − 1 = 3 columnas no nulas, sin embargo su rango no es 3, ya que
⎛1
⎜
1
Rang ( B) = Rang ⎜
⎜1
⎜⎜
⎝1
1
1
1
1
0
1
1
1
0⎞
⎛1
⎟
⎜
0⎟
1
= Rang ⎜
⎜1
0⎟
⎟⎟
⎜⎜
0⎠
⎝1
0
1
1
1
0
0
0
0
0⎞
⎟
0⎟
=2
0⎟
⎟
0 ⎟⎠
b) Falso.
Como contraejemplo nos vale la matriz B del caso a).
c) Falso.
Como contraejemplo tenemos las matrices A y B del caso a):
MATEMÁTICAS I
63
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
A = B =0
d) Verdadero.
Si una matriz tiene una de sus columnas o una de sus filas idénticamente
nula, su determinante vale 0.
12.- Sean
y
A
B
∈ M ( R)
con
A.B = A . De los tres
apartados siguientes demostrar el que sea verdadero y dar
contraejemplos para los apartados falsos.
a) A ≠ 0 ⇒ B = 1.
b) B ≠ 0 ⇒ A = 1
c) A ≠ 0 ⇒ A = 1
SOLUCIÓN:
a) Verdadera.
A.B = A . B
AB = A
=
A A ≠0⇒ B =
A
A
=1
b) Falsa.
Como contraejemplo valdría el siguiente:
⎛ 2 0⎞
A=⎜
⎟
⎝0 1⎠
y
⎛1 0⎞
B=⎜
⎟ en este caso tenemos que
⎝0 1⎠
A.B = A y
además B = 1 ≠ 0 , sin embargo tenemos que A = 2 ≠ 1
c) Falsa.
Como contraejemplo nos vale el mismo que el del apartado b).
64
MATEMÁTICAS I
Matrices y Determinantes
BIBLIOGRAFIA
ANZOLA, M.; CARUNCHO, J.; PÉREZ-CANALES, G. (1981).
Problemas de Álgebra (Tomos 1-7). Madrid. SSAG.
BURGOS, J. (1999).
Álgebra Lineal y Geometría Cartesiana. Madrid.
McGraw-Hill.
CARBO, R.; DOMINGO, LL. (1987). Álgebra Matricial y Lineal.
España. McGraw-Hill.
DE LA VILLA, A. (1994). Problemas de Álgebra. Madrid. Clagsa.
ESPADA BROS, E. (1984). Problemas resueltos de Álgebra. Barcelona.
EUNIBAR.
FLAQUER, J; OLAIZOLA, J; OLAIZOLA, J. (1996). Curso de Álgebra
Lineal. Navarra EUNSA.
FRALEIGH, J.B.; BEAUREGARD, R.A. (1989). Álgebra Lineal.
U.S.A. Addison-Wesley Iberoamericana.
GARCÍA, J.; LÓPEZ, M. (1990). Álgebra Lineal y Geometría. Alcoy.
Marfil.
GRANERO, F. (1994). Álgebra y Geometría Analítica. Madrid .
McGraw-Hill. GROSSMANN, S.I. (1996). Álgebra Lineal con aplicaciones.
México. McGraw-Hill.
GUERRA, N.; LÓPEZ, B. (1999). Problemas resueltos tipo test de
Álgebra Lineal (Con esquemas teóricos). Las Palmas de G.C. El Libro
Técnico.
MATEMÁTICAS I
65
Guerra, N.; López, B.; Quintana, M.P.; Suárez, A.
66
MATEMÁTICAS I