Soluciones a los Ejercicios del Segundo Parcial de Topolog´ıa I

Soluciones a los Ejercicios del Segundo Parcial de
Topologı́a I
Grado en Matemáticas, Grupo A
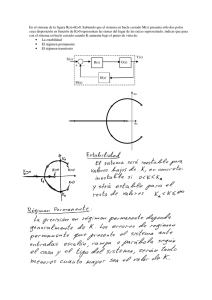
(1) Llamemos X = [0, 1] × {−1, 1} ⊆ R2 , y dotemos a este conjunto de la
topologı́a euclidiana inducida por (R2 , τu ). Consideremos la aplicación
(
cos(πx), sen(πx)
si y = 1
1
f : (X, τu ) → (S , τu ), f (x, y) =
cos(πx), −sen(πx)
si y = −1
Probar que
(a) f es una identificación.
(b) (X/R, τu /R) ∼
= (S1 , τu ), donde R es la relación de equivalencia en X
dada por


(x1 , y1 ) = (x2 , y2 )
(x1 , y1 )R(x2 , y2 ) ⇐⇒
o


x1 = x2 ∈ {0, 1}
Solución:
Item (a). Denotemos por F1 = [0, 1] × {−1} y F2 = [0, 1] × {1}. Como Fj es
producto de dos cerrados en (R, τu ), Fj es cerrado en (R2 , τu ), y por tanto,
también en (X, τu ), j = 1, 2. Además nótese que X = F1 ∪ F2 y F1 ∩ F2 = ∅.
Por otra parte, la función f |Fj : (Fj , τu ) → (S1 , τu ) es continua, j = 1, 2.
En efecto, téngase en cuenta que f |Fj no es sino la restricción a Fj de la
aplicación continua h : (R, τu ) → (S1 , τu ), h(x) = cos(πx), (−1)j sen(πx) ,
j = 1, 2. Concluimos que el espacio (X, τu ) se descompone como unión de
dos cerrados disjuntos sobre los que la restricción de f es continua, y en
consecuencia, que f : (X, τ ) → S1 es continua.
Como f (F1 ) es la semicircunferencia {(x, y) ∈ S1 : y ≤ 0}, y análogamente
f (F2 ) = {(x, y) ∈ S1 : y ≥ 0}, deducimos que f (X) = f (F1 ) ∪ f (F2 ) = S1 ,
esto es, que f es sobreyectiva.
Finalmente observemos que X es compacto en (R2 , τu ). En efecto, X es
cerrado en (R2 , τu ) por ser unión de dos cerrados de (R2 , τu ) (a saber, F1 y
F2 ), y es acotado respecto a la métrica euclidiana
ya que claramente X está
contenido en la bola euclidiana B (0, 0), 2 de centro el origen y radio 2. Por
el Teorema de Heine-Borel concluimos lo deseado. Ası́ pues, la aplicación
f tiene por dominio un espacio compacto y codominio un espacio T2 (S1 es
1
un subespacio topológico de (R2 , τu ) que es T2 , y por tanto también es T2 ),
por lo quef ha de ser cerrada.
Concluimos por tanto que f es continua, sobreyectiva y cerrada, por tanto
una identificación.
Item (b). Por el anterior apartado sabemos que f es una identificación.
Determinemos la relación de equivalencia Rf inducida por f .
Tomemos (x1 , y1 ), (x2 , y2 ) ∈ X y supongamos que (x1 , y1 )Rf (x2 , y2 ), esto
es, que f (x1 , y1 ) = f (x2 , y2 ). Discutamos dos casos: x1 ∈]0, 1[ y x1 ∈ {0, 1}.
Asumamos primero que x1 ∈]0, 1[, o equivalentemente, que sen(πx1 ) 6= 0.
Los hechos:
• sen(πx) > 0 para todo x ∈]0, 1[ y
• la segunda coordenada de f (x1 , y1 ) y f (x2 , y2 ) coinciden,
implican que y1 = y2 , y por supuesto y1 = y2 ∈ {−1, 1}. De aquı́ que,
usando de nuevo que f (x1 , y1 ) = f (x2 , y2 ), deducimos que cos(πx1 ) =
cos(πx2 ), sen(πx1 ) = sen(πx2 ). Por tanto πx2 − πx1 = 2πm para algún
m ∈ Z, de donde al ser x1 , x2 ∈]0, 1[ inferimos que x1 = x2 . En conclusión
(x1 , y1 ) = (x2 , y2 ), y por tanto, (x1 , y1 )R(x2 , y2 ).
Asumamos ahora que x1 ∈ {0, 1}, o equivalentemente que sen(πx1 ) = 0.
Como f (x1 , y1 ) = f (x2 , y2 ) deducimos que sen(πx2 ) = 0 igualmente, de
donde x2 ∈ {0, 1}. Por otra parte, la identidad cos(πx1 ) = cos(πx2 ) implica
necesariamente que x1 = x2 , de donde (x1 , y1 )R(x2 , y2 ).
Concluimos pues que Rf = R. Por teorı́a general de identificaciones existe
un homeomorfismo
fˆ: (X/Rf , τu /Rf ) ≡ (X/R, τu /R) → (S1 , τu )
satisfaciendo fˆ ◦ p = f , donde p : (X, τu ) → (X/Rf , τu /Rf ) ≡ (X/R, τu /R)
es la proyección natural al cociente.
(2) Estudiar la conexión de los siguientes espacios topológicos, todos dotados
de sus correspondientes topologı́as euclidianas:
(a) (Z × R) ∪ ∆, donde ∆ = {(x, x) ∈ R2 : x ∈ R}.
(b) {(x, y, z) ∈ R3 : x2 + y 2 + 1 = z 2 }.
(c) R3 − {(0, 0, z) ∈ R3 : z ∈ R}.
Solución:
Item (a). Llamemos X = (Z × R) ∪ ∆ y Xm = ({m} × R) ∪ ∆ para cada
m ∈ Z.
Primero observermos que (∆, τu ) es homeomorfo a (R, τu ). Para ello basta
con considerar f : (∆, τu ) → (R, τu ), f (x, x) = x. Es fácil observar que f es
continua (restricción a ∆ de la primera proyección p1 : (R2 , τu ) → (R, τu ),
2
p1 (x, y) = x), al igual que su inversa f −1 : (R, τu ) → ∆, f −1 (x, x). De hecho,
∆ no es sino el grafo de la aplicación identidad Id : (R, τu ) → (R, τu ). Por un
razonamiento similar se puede comprobar que ({m} × R, τu ) es homeomorfo
a (R, τu ), en este caso basta con restringir a {m} × R la segunda proyección
p2 : (R2 , τu ) → (R, τu ), p2 (x, y) = y para generar un homeomorfismo.
Como la conexión es un invariante topológico y (R, τu ) es conexo, inferimos
que {m} × R y ∆ con conexos en (R‘2, τu ). Al ser {(m, m)} = ({m} × R) ∩
∆ 6= ∅, deducimos que Xm es conexos en (R2 , τu ), y esto para cada m ∈ Z.
Para concluir, el espacio X es unión de subespacios conexos respecto a la
topologı́a euclidiana (a saber, Xm , m ∈ Z), siendo cada dos de ellos con
intersección no vacı́a: ∆ ⊆ Xm1 ∩ Xm2 6= ∅. Por un criterio estandard de
conexión, X es conexo en (R2 , τu ).
Item (b). Escribamos Y = {(x, y, z) ∈ R3 : x2 +y 2 +1 = z 2 }, y notemos que
Y ∩ {(x, y, z) ∈ R3 : z ∈] − 1, 1[} = ∅. Si llamamos Y+ = {(x, y, z) ∈ R3 :
x2 + y 2 + 1 = z 2 , z > 0} e Y− = {(x, y, z) ∈ R3 : x2 + y 2 + 1 = z 2 , z < 0},
claramente Y+ e Y− son abiertos de (Y, τu ) por obtenerse, respectivamente,
como la intersección de Y con los hiperplanos abiertos {z > 0} y {z < 0}
de R3 . Además, Y = Y+ ∪ Y− e Y+ ∩ Y− = ∅. Ası́ pues, Y puede ponerse
como unión de dos abiertos no vacı́os y disjuntos, y por tanto no es conexo.
Item (c). Obsérvese que R3 − {(0, 0, z) ∈ R3 : z ∈ R} = (R2 − {(0, 0)}) × R.
Es fácil ver que (R2 −{(0, 0)}, τu ) es conexo. En efecto, de hecho este espacio
es homeomorfo al producto de conexos S1 ×]0, +∞[, o alternativamente,
coincide con un espacio euclidiano de dimensión ≥ 2 menos una cantidad
numerable (uno sólo en este caso) de puntos. Análogamente es conocido
que (R, τu ) es conexo pues se trata de un intervalo real.
En conclusión, R3 − {(0, 0, z) ∈ R3 : z ∈ R} = (R2 − {(0, 0)}) × R es conexo
por ser producto de dos espacios conexos.
(3) Estudiar la compacidad de los siguientes espacios topológicos, todos dotados
de sus correspondientes topologı́as euclidianas:
(a) H = {(x, y, z) ∈ R3 : x2 + 2y 2 + 3z 2 ≤ 1}.
(b) X = {(x, y) ∈ R2 : x2 + ey ≤ 1}.
(c) Y = ∪n∈N [−1/n, 1/n] × {1/n} ∪ {(0, 0)}.
Solución:
Item (a). Veamos que Hes cerrado en (R3 , τu ) y acotado respecto de la
métrica euclidiana. Por el Teorema de Heine-Borel, H será compacto.
Para comprobar que H es cerrado, considero la aplicación f : (R3 , τu ) →
(R, τu ), f (x, y, z) = x2 + 2y 2 + 3z 2 . Esta aplicación es continua por álgebra
elemental de aplicaciones continuas, por tanto H = f −1 (]−∞, 1]) es cerrado
al ser la imagen inversa por una aplicación continua de un intervalo cerrado
de la recta real.
3
Para comprobar que H es acotado, obsérvese que para todo (x, y, z) ∈ H
tenemos que
x2 + y 2 + z 2 ≤ (x2 + y 2 + z 2 ) + (y 2 + 2z 2 ) = x2 + 2y 2 + 3z 2 ≤ 1,
y por tanto H ⊆ B (0, 0, 0), 1 , donde B (0, 0, 0), 1 representa la bola
euclidiana cerrada de centro el origen y radio 1.
Item (b). La sucesión {(0, −n)}n∈N está contenida en X y es divergente,
por lo que X no es acotado en R2 respecto de la métrica euclidiana. Por el
Teorema de Heine-Borel X no es un subconjunto compacto de (R2 , τu ).
Item (c). En este caso Y es compacto en (R2 , τu ). Al igual que antes,
usaremos el Teorema de Heine-Borel para comprobarlo.
Primero, observemos que Y es cerrado en (R2 , τu ). Una forma de verlo es
la siguiente.
Primero, observemos que el conjunto T = {(x, y) ∈ R2 : y ≥ |x|} es cerrado
en el plano (R2 , τu ). Para ello, basta con observar que T = f −1 ([0+, ∞[),
donde f es la función continua f : (R2 , τu ) → (R, τu ), f (x, y) = y − |x|. A
continuación, consideremos la función continua g : (T, τu ) → R, g(x, y) = y
(g no es sino la restricción a T de la segunda proyección p2 : (R2 , τu ) →
(R, τu ), p2 (x, y) = y), y observemos que Y = g −1 ({1/n, n ∈ N} ∪ {0}).
Como el cojunto {1/n, n ∈ N}∪{0} es cerrado en (R, τu ), deducimos que Y
es cerrado en (T, τu ) (imagen inversa por la función continua g del conjunto
cerrado {1/n, n ∈ N} ∪ {0}). En particular, Y es cerrado en (R2 , τu ) ya
que T es cerrado en (R2 , τu ).
Por último, comprobemos
que Y es acotado.
Para ello basta con observar
que Y ⊆ B (0, 0), 2 , donde B (0, 0), 2 representa a la bola euclidiana
cerrada de centro el origen y radio 2. De hecho, por trigonometrı́a elemental
x2 + y 2 + z 2 ≤ 2 para todo (x, y, z) ∈ Y , ya que Y está contenido en el
rectángulo [−1, 1] × [0, 1].
4