Desarrollo de algunos problemas de cálculo
Anuncio
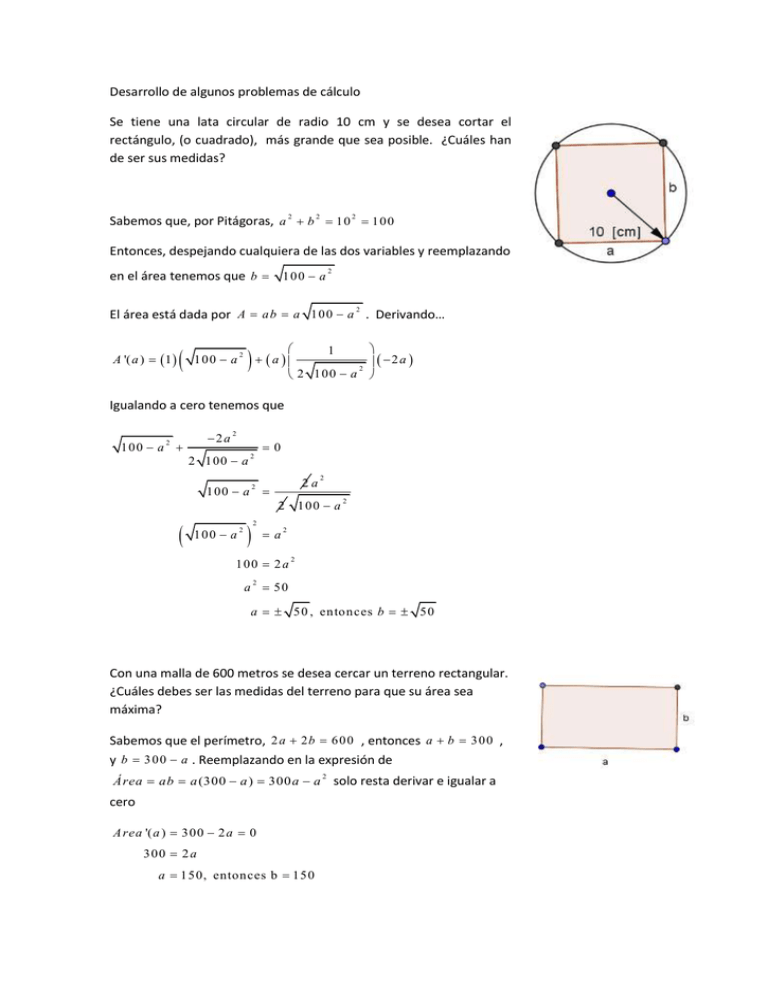
Desarrollo de algunos problemas de cálculo Se tiene una lata circular de radio 10 cm y se desea cortar el rectángulo, (o cuadrado), más grande que sea posible. ¿Cuáles han de ser sus medidas? Sabemos que, por Pitágoras, a 2 b 2 10 2 100 Entonces, despejando cualquiera de las dos variables y reemplazando 2 en el área tenemos que b 100 a 2 El área está dada por A a b a 1 0 0 a . Derivando… A '( a ) 1 100 a 2 a 2 2a 2 100 a 1 Igualando a cero tenemos que 100 a 2a 2 2 2 100 a 0 2 100 a 2a 2 100 a 2 2 2 100 a 2 2 a 2 100 2 a 2 a 50 2 a 50 , entonces b 50 Con una malla de 600 metros se desea cercar un terreno rectangular. ¿Cuáles debes ser las medidas del terreno para que su área sea máxima? Sabemos que el perímetro, 2 a 2 b 6 0 0 , entonces a b 3 0 0 , y b 3 0 0 a . Reemplazando en la expresión de Área ab a (300 a ) 300 a a solo resta derivar e igualar a 2 cero A rea '( a ) 300 2 a 0 300 2 a a 150, entonces b 150 A las 3:00 PM la persona A se encuentra a 150 Km. Al oriente de la persona B. La persona A se dirige al poniente a razón de 10 Km./h y la persona B hacia el sur a 20 Km./h. Si ambos mantienen sus rumbos y velocidades ¿Cuándo estarán más próximos entre sí? ¿Cuál es la distancia mínima a la que se acercarían? Consideremos A o y B o las posiciones de las personas a las 3:00 PM y A 1 y B1 sus posiciones X horas después. La distancia recorrida en X horas es 10X y 20X respectivamente. La distancia entre las dos personas (Y) se puede representar en la ecuación: y 20 x 150 – 10 x de 2 2 2 donde: 20 x y 2 1 5 0 – 1 0 x 2 Desarrollando yx 400 x 22500 - 3000 x 100 x 2 2 500 x -3000 x 22500 2 Derivando y ' x 1 2 500 x -3000 x 22500 2 1000 x 3000 Igualando a cero y ' x 1000 x 3000 2 500 x -3000 x 22500 0 es fácil ver que x 3 2 Para X = 3 existe un mínimo en la función, por lo tanto después de tres horas se encuentran más próximos entre si, es decir, a las 6:00 PM La distancia que las separa en ese momento es: y 60 2 150 – 30 2 18000 134,164 m etros De una lámina de 120 cm. X 75 cm. Se desea construir una caja sin tapa, del mayor volumen posible recortando cuadrados iguales de las esquinas de la lámina y doblando hacia arriba las salientes para tomar las caras laterales. ¿Cuáles deben de ser las dimensiones de la caja para que su volumen sea máximo? ¿Cuál es el volumen máximo que puede contener? Las figuras muestran los cortes que se hacen a la lámina y la figura de la caja resultante. Al asignar X a la altura de la caja y V a su volumen, se expresa algebraicamente: V x 120 – 2 x 75 – 2 x x 4 x 390 x 9000 x 3 2 No se le puede recortar a la lámina más de 37.5 cm., por lo que la altura debe estar en el intervalo: 0<X<37.5 Calculando el máximo en la función V ' x 12 x 780 x 9000 . Igualando a cero y resolviendo se llega a los valores 2 X1 = 50 y X2 = 15. Puede descartarse el valor X = 50 por estar fuera del intervalo: 0< X<37.5 Al realizar la segunda derivada y evaluando en ella las dos raíces se observa que V ” x 24 x – 780 V ” 5 0 2 4 5 0 7 8 0 4 2 0 por ser positivo, hay un mínimo para X = 50 V ” 15 2 4 15 – 780 420 por lo tanto se encuentra el máximo que buscamos en x = 15 3 2 Al sustituir en la función V x 4 x 390 x 9000 x el valor X = 15, encontramos el volumen máximo de la caja: V 15 4 15 390 15 3 2 9000 15 60 750 cm La altura debe ser X = 15cm La longitud es (120 – 2X) = 120 – 2(15) = 90 cm. La anchura es (75 – 2X) = 75 – 2(15) = 45 cm. 3