PROBLEMAS RESUELTOS DE+CAMPO MAGNETICO EN+EL+VACIO
Anuncio
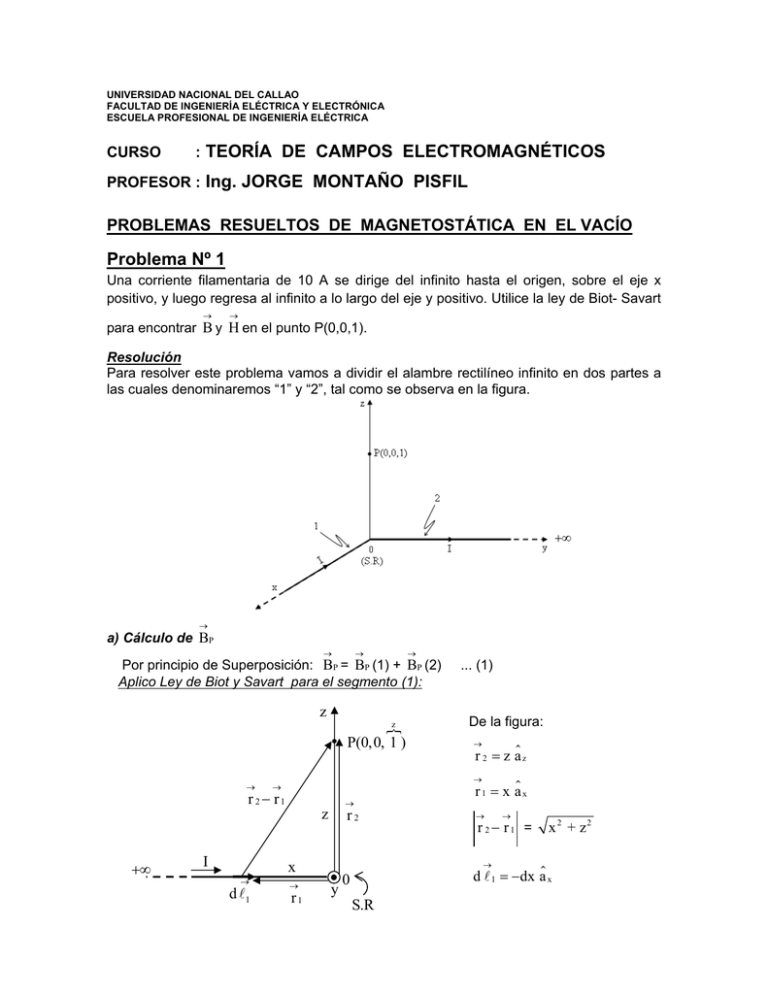
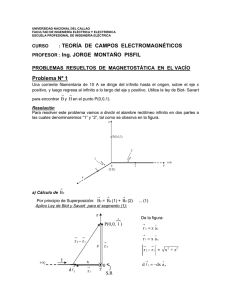
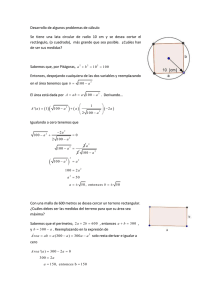
UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA ESCUELA PROFESIONAL DE INGENIERÍA ELÉCTRICA CURSO : TEORÍA DE CAMPOS ELECTROMAGNÉTICOS PROFESOR : Ing. JORGE MONTAÑO PISFIL PROBLEMAS RESUELTOS DE MAGNETOSTÁTICA EN EL VACÍO Problema Nº 1 Una corriente filamentaria de 10 A se dirige del infinito hasta el origen, sobre el eje x positivo, y luego regresa al infinito a lo largo del eje y positivo. Utilice la ley de Biot- Savart para encontrar B y H en el punto P(0,0,1). Resolución Para resolver este problema vamos a dividir el alambre rectilíneo infinito en dos partes a las cuales denominaremos “1” y “2”, tal como se observa en la figura. a) Cálculo de BP Por principio de Superposición: BP = BP (1) + BP (2) Aplico Ley de Biot y Savart para el segmento (1): z I z r2 x d 1 De la figura: r 2 z a z r 2 r1 z P(0,0, 1 ) ... (1) r1 r 1 x a x y r 2 r1 = x 2 + z2 d 1 dx a x 0 S.R BP (1) o I 4π Reemplazando: BP (1) ... (2) 3 r 2 r1 BP (1) d 1 ( r 2 r 1 ) 0 dxa x (za z xa x ) o I zdx a y 2 2 3/ 2 2 4π (x + z ) 4π (x + z 2 )3/ 2 o I 0 o I 4π*10-7 (10) ay a y (106 T) a y 4π z 4π (1) Aplico Ley de Biot y Savart para el segmento (2): De la figura: z z P(0,0, 1 ) r 2 z a z r 2 r1 z r2 r 1 y a y r 2 r1 = BP (2) 4π d 2 ( r 2 r 1) r 2 r1 ... (3) 3 Reemplazando: BP (2) BP (2) d 1 dy a y d 2 r1 o I S.R x I y 0 o I dya y (za z ya y ) 4π 2 2 3/ 2 (y + z ) 0 o I 4π zdy (y + z ) 2 2 3/ 2 0 o I 4π*10-7 (10) ax a x (106 T) a x 4π z 4π (1) Finalmente, reemplazo B P (1) y B P (2) en la ecuación (1) y obtengo: BP = (106 T)(a x a y ) b) Cálculo de H P : y2 + z2 H P = H P (1) + H P (2) ; siendo : H B 0 a x Reemplazando obtenemos: A H P 0, 796 (a x a y ) m Problema Nº 2 Encuentre H en P (2; 3; 5) en coordenadas cartesianas, si existe un filamento portador de corriente de longitud infinita, que pasa a través del origen y el punto C . Una corriente de 50 A se dirige desde el origen hasta C, donde la localización de C es (0; 0; 1). Resolución: 1er Caso: Cálculo de H en el punto P (2; 3; 5) debido a I = 50 A que se dirige desde el origen hasta C (0; 0; 1). + z I Por simetría de la figura se cumple que: 5 Es decir, en los puntos P y Q el d P(2,3,5) vector r 2 r1 r1 S.R intensidad de campo magnético tiene la misma magnitud 3 0 y y la misma dirección. Por lo tanto, el r2 2 HP HQ valor calculado de H en el punto Q Q es el mismo valor que corresponde x a H en el punto P. I d ( r 2 r 1 ) Por Ley de Biot y Savart: H Q 4π 3 ... (1) r 2 r1 De la figura: d = dz a z ; r 2 = xa x + ya y = 2a x + 3a y r 1 z a Z ; r 2 r1 x 2 y2 z2 13 z 2 En (1): I dz a z (2a x + 3a y za z ) I dz dz y 3I a a 2 3/2 2 3/2 2 3/2 x 4π (13 + z ) 2π (13 + z ) 4π (13 + z ) I 2 3I 2 50 75 ay ax ay ax 2π 13 4π 13 13π 13π HQ = HQ H Q = (1,224 a y 1,84 a x ) A/m Otro método: Por ley de Ampere Vista de planta r I 3 H d 2 Q curva "C " o trayectoria Amperiana (es aquella donde el x módulo de H es cte.) Por Ley de Ampere: H. d Ienc C H (2r) = I H= I 2π r y H Vectorialmente: I a 2π r De la figura: a Sen a x Cos a y Luego: I Sen a x Cos a y H 2π r H (1, 224 a y 1,84 a x ) A/m Problema Nº 3 Considere la línea de transmisión de dos hilos cuya sección transversal se ilustra en la figura. Cada uno de los alambres tiene 2 cm de radio y están separados por 10 cm. Por el alambre con centro en (0,0) fluye una corriente de 5 A, Mientras que por el otro, centrado en (10cm, 0) fluye la corriente de retorno. Calcule B y H en: a) (5 cm, 0) ; b) (10 cm, 5 cm) y I I 4 cm x 10 cm Resolución Llamaremos I1 a la corriente de ida e I 2 a la corriente de retorno, como se muestra en la figura siguiente. y I1 5A 4 cm I 2 5A x 10 cm a) Cálculo de B y H en el punto (5cm; 0): En el punto P (5 cm; 0) se crean dos Campos magnéticos, porque hay dos corrientes eléctricas. A continuación se muestran los vectores B1 y B2 , debido a las corrientes I1 e I2 . B1 B2 I1 5A I 2 5A P(5cm,0) r r trayectoria Amperiana Por el principio de Superposición aplicado a los campos magnéticos se cumple: Bp = B1 + B2 ... (1) Hallo B1 aplicando ley de Ampere C B1 (2 π r) = 0 I1 B1 B. d o I ; I = Iencerrada 0 I1 2π r ; Vectorialmente: B1 0 I1 ay 2π r Análogamente tenemos que B2 quedará expresado por: B2 Reemplazo en (1): Bp = 2 B1 ; porque B2 = B1 (dado que I 2 = I1 ) BP 0 I1 a y (4 10 5 a y ) T r 0 I2 ay 2π r B Para hallar H aplico: H = (en el vacío) 0 HP BP 0 I1 A a y (31,83 a y ) r m b) Cálculo de B y H en el punto Q (10cm; 5cm) En el punto Q , los vectores B1 y B2 tienen las direcciones mostradas en la figura siguiente. Q x Por el principio de Superposición: BQ = B1 + B2 ... (2) Donde: * B2 =B2 a x ; B2 = o I2 módulo de B para un alambre 2π r2 B2 0 I 2 a X (2 105 a X ) T 2r2 o I1 I B1 = 2π r1 * B1 = B1 a B1 = o 1 ( Sen a x Cos a y ) 2π r1 a Sen a x Cos a y B1 ( 0,4 10 5 a x 0,8 10 5 a y ) T Finalmente, reemplazando en (2): 5 5 BQ (1,6 10 a x 0,8 10 a y ) T Para hallar H aplico: H = B 0 (en el vacío) HQ BQ 0 (12,74 a x 6,366 a y ) A m Problema Nº 4 Un conductor sólido tiene una sección transversal circular de radio 1 mm , centrado en el eje z, y porta una corriente total distribuida uniformemente de 10 A en la dirección a z . Hay una corriente laminar región: a) 0 K 1000 a z A/m en 2mm . Encontrar H en la 1mm ; b) 1 2mm ; c) 2 4mm d) ¿Qué valor de la corriente laminar debe estar colocada en 4mm ; tal que H 0 para 4mm ? Resolución: De acuerdo con lo señalado en el enunciado, la figura correspondiente es: a) Cálculo de H en la región 0 1mm Por ley de Ampere: Sección transversal del conductor sólido H. d I ; I = Iencerrada H (2 ) I encerrada . . . (1) Hallo I encerrada : Si la corriente está uniformemente distribuida, se cumple que: I1 1mm trayectoria Amperiana d H J cte I I1 enc2. 3 2 (110 ) I enc = 107 π 2 Reemplazando en (1): H (2 ) 107 2 H (5 106 a ) A m b) Cálculo de H en la región 1 mm 2 mm En este caso: H 5 A I1 H a 2π m c) Cálculo de H en la región 2 mm 4 mm Sección transversal Por ley de Ampère : H.d Ienc H(2π ) = I1 + I2 .... (2) I1 I2 1mm 2mm Donde: I1 = 10 A A I 2 = I LAMINAR = 1000 a z 2π(2 103 )m 4π A m TOTAL En (2): H(2π ) = 10π A+ ( 4π A) = 6π A = Ienc trayectoria H Amperiana H 3 , 3 A H a m d) Piden K1 tal que el H ( 4mm) 0 H( 4mm) 0 si I enc = 0 Del ejercicio anterior se obtuvo: Ienc = 6π Luego : K1 = 6π + Ienc 1 = 0 I enc 1 6π A A 6π A a = 750 a z z 2π(4 103m) m Problema Nº 5 Una corriente I fluye longitudinalmente por una lámina conductora delgada y muy larga de anchura a, como se muestra en la figura. Suponga que la corriente fluye hacia el interior del papel y determine la densidad de flujo magnético B en los puntos P1 (0; d1) y P2 (a + d2; 0). y P1 d1 I P2 a x d2 Resolución: a) Cálculo de B en el punto P1 (0; d1) : Para calcular B en el punto P1 , debido a la corriente I que fluye por la lámina conductora delgada y muy larga, analizo a partir de un elemento diferencial de la forma de un hilo infinito, tal como se indica en la figura mostrada a continuación. y dB P1 a r d1 dI x z Se sabe : B H ilo En nuestro caso: 0I 2π r , donde: r es la distancia perpendicular al hilo infinito. dB (Lámina) 0 dI d B (Lámina) 2π r r= d +x ... (1) dB I dx a 2 1 2π r y donde: dI = 0 dI u P1 2 d1 θ Línea magnética θ r dI de la figura : x u Cosθ a x Senθ a y x dx a Reemplazando en (1): 0 I dx d B(Lámina ) 2π a d x Integrando tenemos: B(Lámina ) B ( Lá min a ) 2 1 0 I 2π a 0 I 2 (Cosθ a x Senθ a y ) (Cosθ a x Senθ a y )dx d12 x 2 a d1dx ax 2 2π a 0 d1 x 2 a xdx a 2 2 y 1 x d 0 Resolviendo, obtenemos: B(Lámina ) 0 I d 2 x2 a Arctg a x Ln 1 2π a d1 d1 a y b) Cálculo de B en el punto P2 (a + d2; 0) En este caso procedemos de manera similar que en a). y a dx dI P2 x r x d2 z Ya sabemos que la magnitud de B , debido a una corriente I , que circula por un hilo infinito, a una distancia r de dicho hilo, viene dada por: B 0I 2π r En nuestro caso, este campo “B” será un diferencial de campo para la lámina, es decir: dB (Lámina) 0 dI 2π r , donde: r = (a + d2 – x). Además se cumple: I dI I = dI = dx , a dx a Luego: dB(Lámina ) 0 I dx 2π a(a + d 2 x) y Vectorialmente sería: d B(Lámina ) 0 I dx 2π a(a + d 2 x) Línea magnética u ... (2) dI dx a P2 r x d2 dB Del gráfico: u a y Reemplazando en (2) e integrando: B(Lámina ) 0 I a dx 2π a (a + d 0 2 x) Resolviendo la integral obtenemos: (a y ) , B(Lámina ) 0 I a + d2 Ln ay 2π a d 2 Problema Nº 6 Una corriente continua I fluye por un alambre recto de longitud 2L. Calcule la inducción magnética B en un punto localizado a una distancia “ r ” del alambre y en el plano que lo divide en dos segmentos iguales. Determine primero el vector potencial magnético "A" . Resolución: Por tratarse de un alambre recto de longitud 2L, la figura es: Aplicando la regla de la mano derecha el z vector B está entrando al punto P. +L Vista de Planta d r1 z B r2 0 2L r 2 r1 r P y I r P Para un que: A L con corriente I , se cumple S.R I Hilo (r ) = o I 4π d r 2 r1 De la figura: d dz a z ; r 2 r a y ; Reemplazando: A (r ) = o I 4π dz a z +L z = L r2 + z2 A (r ) = r 1 z a z ; r 2 r1 = o I r 2 z2 L Ln z + z 2 + r 2 a z L 4π Ln 4π o I L2 + r 2 L az L2 + r 2 L Hallo B(r ) ; aplicando rotacional : B(r ) A (r ) Se cumple: En este caso A depende de la coordenada “ r ”, por lo tanto su rotacional en coordenadas cilíndricas viene dado por: B(r) A (r) A (z) a r Resolviendo se obtiene: o I L (r ) 2π r L2 + r 2 a