PRODUCTO CARTESIANO DE DOS CONJUNTOS Dados dos
Anuncio
_______________________________________________________________________________
TERCER BIMESTRE
SEMANA 19
MATEMATICA III
3ro. Básico
PRODUCTO CARTESIANO DE DOS CONJUNTOS
Dados dos conjuntos A y B, el producto cartesianos de estos dos conjuntos es el
conjunto formado por todos los pares ordenados (a,b) donde a es un elemento de A y b
es un elemento de B.
Ejemplo: Sean A = {a, b, c} y B = {1, 2} dos conjuntos. El producto cartesiano A x B =
(a,1), (a,2), (b,1), (b,2), (c,1), (c,2) El cardinal (número de elementos) del producto
cartesiano es el producto de los cardinales de los dos conjuntos, |A x B| = |A| x |B|
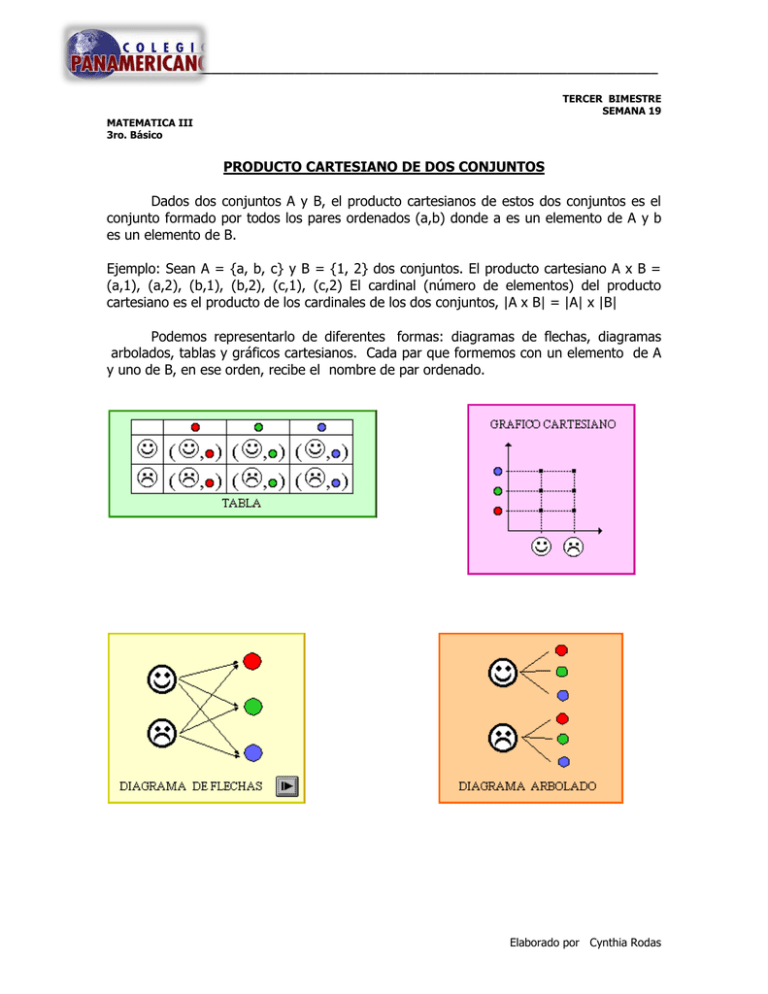
Podemos representarlo de diferentes formas: diagramas de flechas, diagramas
arbolados, tablas y gráficos cartesianos. Cada par que formemos con un elemento de A
y uno de B, en ese orden, recibe el nombre de par ordenado.
Elaborado por Cynthia Rodas
_______________________________________________________________________________
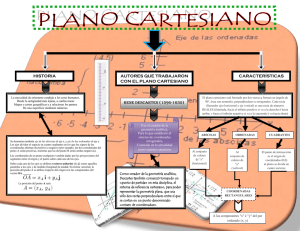
EL PLANO CARTESIANO
El plano cartesiano está formado por dos rectas numéricas, una horizontal y otra
vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de
las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan
recibe el nombre de origen.
El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales
se representan por sus coordenadas o pares ordenados. Las coordenadas se forman
asociando un valor del eje de las "X" y uno de las "Y", respectivamente, esto indica que un
punto se puede ubicar en el plano cartesiano con base en sus coordenadas, lo cual se
representa como:
P (x, y)
Para localizar puntos en el plano cartesiano se debe llevar a cabo el siguiente
procedimiento:
1. Para localizar la abscisa o valor de x, se cuentan las unidades correspondientes
hacia la derecha si son positivas o hacia a izquierda si son negativas, a partir del
punto de origen, en este caso el cero.
2. Desde donde se localiza el valor de x, se cuentan las unidades correspondientes
hacia arriba si son positivas o hacia abajo, si son negativas y de esta forma se
localiza cualquier punto dadas sus coordenadas.
Elaborado por Cynthia Rodas
_______________________________________________________________________________
Ejemplos:
Localizar el punto A (-4, 5) en el plano cartesiano. Este procedimiento también se emplea
cuando se requiere determinar las coordenadas de cualquier punto que esté en el plano
cartesiano.
Determinar las coordenadas del punto M.
Las coordenadas del punto M son (3,-5).
De lo anterior se concluye que:
Para determinar las coordenadas de un punto o localizarlo en el plano cartesiano,
se encuentran unidades correspondientes en el eje de las x hacia la derecha o hacia la
izquierda y luego las unidades del eje de las y hacia arriba o hacia abajo, según sean
positivas o negativas, respectivamente.
Elaborado por Cynthia Rodas
_______________________________________________________________________________
Doña Lupe nos ha dicho que su farmacia está dentro del centro de la ciudad.
Supongamos que deseamos saber la ubicación exacta de la farmacia de Doña Lupe Una
vez que ya estamos en el centro le preguntamos a un policía para que nos oriente. El
policía nos ha dicho que caminemos 5 cuadras hacía el este y 6 cuadras hacía el norte
para llegar a la farmacia. La cantidad de cuadras que tenemos que caminar las podemos
entender como coordenadas en un plano cartesiano.
Lo anterior lo podemos expresar en un plano cartesiano de la siguiente manera:
Para el problema planteado, el origen del plano será el punto de partida que es en donde
le preguntamos al policía sobre la ubicación de la farmacia.
Gráfica de la Función Exponencial
En relación con las propiedades 7 y 8, enunciadas en el teorema, es conveniente
hacer algunos comentarios adicionales.
En primer lugar, en las figuras 1 y 2, aparecen las gráficas de algunas funciones
exponenciales de base a > 1 (fig. 1) y de base a < 1 (fig. 2).
Elaborado por Cynthia Rodas
_______________________________________________________________________________
Note que cuando la base a es mayor que 1,la función exponencial
no está acotada superiormente. Es decir ,
(fig.1)
crece sin límite al aumentar la variable x.
Además, ésta función tiene al cero como extremo inferior. Esto es ,
cuando x toma valores grandes pero negativos.
tiende a cero(0),
Igualmente, cuando la base a < 1, la función exponencial
(fig.2) no está
acotada superiormente, pero su comportamiento para valores grandes de x, en valor
absoluto, es diferente. Así,
y
crece sin límite, al tomar x valores grandes, pero negativos
tiende a cero, cuando la variable x toma valores grandes positivos.
El hecho de ser la función exponencial
con a > 1, estrictamente creciente
(estrictamente decreciente cuando 0 < a < 1), significa que la función exponencial es
inyectiva en su dominio.Este hecho y la continuidad de la función son las condiciones que
se exigen para garantizar la existencia de la función inversa ( función logarítmica), que se
presentan en la próxima sección.
En relación con la propiedad 9, en un sentido, se deduce fácilmente de la definición
de función; y, en otro, del hecho de ser la función exponencial inyectiva.
Observación.
Cuando a = e ,donde e es el número irracional cuya representación decimal con sus
primeras cifras decimales, es e = 2.7182818284….,la función exponencial
,se llama:
función exponencial de base e y, frecuentemente, se denota por Exp( x ) =
.
Elaborado por Cynthia Rodas
_______________________________________________________________________________
FUNCION LOGARITMICA
La función logarítmica en base a es la función inversa de la exponencial en base a.
Propiedades de las funciones logarítmicas
Dominio:
Recorrido:
Es continua.
Los puntos (1, 0) y (a, 1) pertenecen a la gráfica.
Es inyectiva (ninguna imagen tiene más de un original).
Creciente si a>1.
Decreciente si a<1.
Si a > 0
Si 0 < a < 1
Elaborado por Cynthia Rodas
_______________________________________________________________________________
Las gráfica de la función logarítmica es simétrica (respecto a la bisectriz del 1er y
3er cuadrante) de la gráfica de la función exponencial, ya que son funciones reciprocas o
inversas entre sí.
Ejemplo de funciones logarítmicas
Representa la función logarítmica:
1
x
1
/4
1
/2
1
/8
2
1
-
3
f
(x)
1
2
4
8
0
1
2
3
Elaborado por Cynthia Rodas