6 Heteroscedasticidad

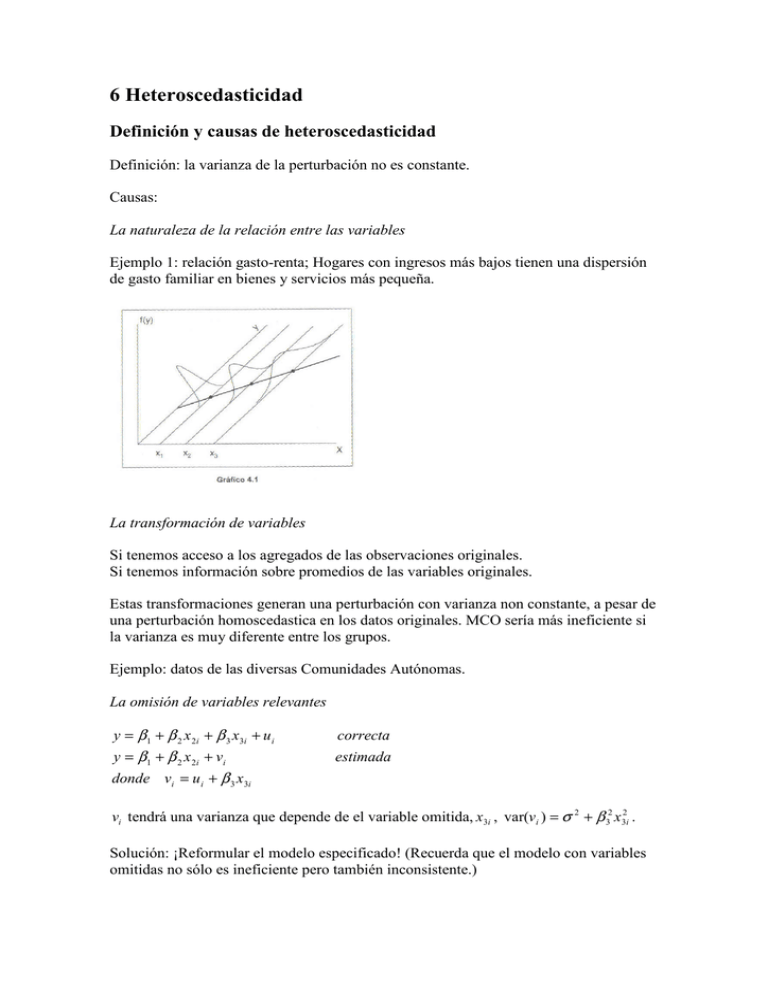
6 Heteroscedasticidad
Definición y causas de heteroscedasticidad
Definición: la varianza de la perturbación no es constante.
Causas:
La naturaleza de la relación entre las variables
Ejemplo 1: relación gasto-renta; Hogares con ingresos más bajos tienen una dispersión
de gasto familiar en bienes y servicios más pequeña.
La transformación de variables
Si tenemos acceso a los agregados de las observaciones originales.
Si tenemos información sobre promedios de las variables originales.
Estas transformaciones generan una perturbación con varianza non constante, a pesar de
una perturbación homoscedastica en los datos originales. MCO sería más ineficiente si
la varianza es muy diferente entre los grupos.
Ejemplo: datos de las diversas Comunidades Autónomas.
La omisión de variables relevantes
y = β 1 + β 2 x 2 i + β 3 x 3i + u i
correcta
y = β 1 + β 2 x 2i + vi
estimada
donde vi = u i + β 3 x3i
vi tendrá una varianza que depende de el variable omitida, x3i , var(vi ) = σ 2 + β 32 x32i .
Solución: ¡Reformular el modelo especificado! (Recuerda que el modelo con variables
omitidas no sólo es ineficiente pero también inconsistente.)
Contrastes de heteroscedasticidad
1. la hipótesis nula es homoscedasticidad.
2. la construcción está basada en los residuos de la estimación por MCO (sin considerar
la posible heteroscedasticidad).
Goldfeld-Quandt
Puede ser útil cuando la heteroscedasticidad depende de una única variable.
(1) Ordena las variables según los valores de la variables posiblemente cause la
heteroscedasticidad.
(2) Elimina p observaciones centrales de la muestra ordenada para crear dos
muestras de idéntico tamaño, n1 = n2 = ( N − p) / 2 . La recomendación es
eliminar aprox. p ≈ N / 3 .
(3) Haz dos regresiones por MCO y calcula V E1 = e1 ' e1 /( n1 − K ) y
V E 2 = e2 ' e2 /( n1 − K ) .
(4) El estadístico de contraste es:
V E2
GQ( F [n2 − k , n1 − k ]) =
V E1
 H 0 : σ i2 = σ u2

2
2
 H A : σ i = σ u xi
donde se supone que la segunda muestra tiene la varianza mayor. GQ se compara con el
valor crítico en la distribución F con [n2 − k , n1 − k ] grados de libertad.
Breusch-Pagan
Puede ser útil cuando la heteroscedasticidad depende de una función de variables.
(1) Estima el modelo original por MCO para conseguir los residuos.
e2
(2) Construye la variable g i = −1 i 2 que se utilizará como variable dependiente
n ∑ ei
en la regresión auxiliar, g i = α1 + α 2 z2i + ... + α p z pi + vi , donde las variables
explicativos son todos las variables exógenos del modelo original que pueda
tener una influencia en la varianza no constante del término de perturbación.
Estima el modelo auxiliar por MCO y calcula VE
( VE = gˆ ' gˆ = ( Zαˆ )' ( Zαˆ ) = αˆ ' Z ' g = g ' Z ( Z ' Z ) −1 Z ' g ).
(3) El estadístico de contraste es:
A
 H 0 : σ i2 = σ u2 = α1

2
 H A : σ i = f (Z )
VE
BP(→ χ [ p − 1]) =
2
2
BP se compara con el valor crítico en la distribución χ 2 con [ p − 1] grados de
libertad.
Una versión modificado (Koenker y Bassett, 1982) es estimar la regresión auxiliar,
ei2 = α1 + α 2 z2i + ... + α p z pi + vi , donde ei2 es el cuadrado de los residuos del modelo
original.
A
BP(m)(→ χ 2 [ p − 1]) =
VEm
m
m=
1 N 2
(ei − n −1 ∑ ei2 ) 2
∑
N i =1
 H 0 : σ i2 = σ u2 = α1

2
 H A : σ i = f (Z )
VEm = (u − u i )' Z(Z' Z) −1 Z' (u − u i ) , donde u = (e12 , e22 ,..., en2 ) , i es una n × 1 columna
de 1s. u = e' e / n ., i = 11 ,...1n .
BP(m) se compara con el valor crítico en la distribución χ 2 con [ p − 1] grados de
libertad. Bajo normalidad los dos contrastes tienen la misma distribución asintótica,
pero VEm puede ser más potente en situaciones cuando esto no este cumplido.
White
Puede ser útil cuando la heteroscedasticidad depende de una función de variables.
(1) Estima el modelo original por MCO para conseguir los residuos.
(2) Los residuos cuadrados se utilizan con variable endógena en una regresión
auxiliar con p = k (k + 1) / 2 regresores: un término independiente, las variables
exógenas del modelo original, el cuadrado de las variables exógenas originales y
los productos por pares de esas variables:
k
k
j =2
j =2
ei2 = α1 + ∑α j x ji + ∑ β j ( x ji ) 2 + ∑ γ s ,t ( xsi xti ) + vi .
(3) El estadístico de contraste es:
s ,t
 H 0 : σ i2 = σ u2 = α 1
W ( χ [ p − 1]) = NR 
2
 H A : σ i = f (Z )
donde R*2 es el coeficiente de determinación de la regresión auxiliar.
2
2
*
W se compara con el valor crítico en la distribución χ 2 con [ p − 1] grados de
libertad.
Nota: Si rechazamos la hipótesis nula, puede ser por causa de una especificación
erróneas en el modelo que da la consecuencia de heteroscedasticidad. Por ejemplo,
una variable tiene un efecto non lineal, o hay interacciones, que no estén incluidas.
Después que el contraste rechaza la hipótesis nula, el contraste no indica que
debemos hacer.
Estimación por MCG: Mínimo cuadrados ponderados.
Estimador mínimo cuadrático generalizado (MCG).
βˆ MCG = ( X ' Ω −1 X ) −1 X ' Ω −1 y
var(βˆ MCG ) = σ 2 ( X ' Ω −1 X ) −1
2
donde : σ 2 = s MCG
=
e´Ω −1e
n−k
MCG es lineal, insesgado y óptimo (ELIO). Bajo el supuesto de normalidad su
distribución muestral es: βˆ MCG → N ( β , σ 2 ( X ' Ω −1 X ) −1 ).
Necesitamos conocer la matriz Ω .
¿Que forma tiene la heteroscedasticidad o autocorrelación?
Si no se sabe: Hay que estimar Ω̂ .
Cuando sepamos Ω se puedo transformar el modelo MCO con perturbaciones no
esféricas para obtener un modelo con perturbación esférica.
Se puede aplicar MCO al modelo transformado.
y = Xβ + u ,
E (uu´) = σ 2 Ω
y* = X * β + u* ,
E (u*u*´) = σ 2 I
donde : y* = Ty, X * = TX, u * = Tu
Hay que elegir la matriz de transformación, T, para que TΩT ' = I (así, T ´T = Ω −1 ).
1. A través de un hipótesis sobre la función de heteroscedasticidad o autocorrelacion.
Ejemplo: heteroscedasticidad: suponemos que la varianza depende de una variable
explicativa.
2. A través de funciones más complicadas.
1a etapa: Estimar los parámetros de la función heteroscedastica para obtener de los
elementos de Ω .
2a etapa: Aplica los formulas del estimador MCG.
[Comparación entre el estimador MCO y MCG.]
Métodos de estimación en presencia de heteroscedasticidad;
Perturbación conocida:
En este caso la perturbación depende de forma monótona de alguna(s) variable(s)
exógena(s), se utilizan las siguientes hipótesis. ( y = β1 + β 2 x 2i + β k x ki + u i )
(i ) σ i2 = σ 2 x 2i
(ii ) σ i2 = σ 2 x 22i
(iii ) σ i2 = σ 2 ( x 2i + x3i )
k
(iv) σ i2 = σ 2 ∑ x ji
j=2
Ejemplos:
(1) la estructura de la varianza para (ii) es la matriz,
 x22,1

2
2 0
E (uu ' ) = σ Ω = σ u
 M

 0
0
2
2, 2
x
M
0
0 

L 0 
O M 

L x22, N 
L
(2) el caso de transformación de variables, agregadas,
 N1
0
2
2
E (uu ' ) = σ Ω = σ u
M

0
0
N2
M
0
L 0 
L 0 
O M 

L NR 
(3) el caso de transformación de variables, promedios,
0
1 / N1
 0
1/ N 2
E (uu ' ) = σ 2Ω = σ u2 
 M
M

0
 0
L
0 
L
0 
O
M 

L 1/ N R 
Con esta información, para ejemplo (1) se defina la matriz T para transformar el
modelo.
1 / x22,1
0

0
1 / x22, 2
−1

Ω =
 M
M

0
 0
0 

L
0 
O
M 

L 1 / x22, N 
L
Recuerda que T ´T = Ω −1 .
1 / x2,1
0

0
1 / x2, 2
T =
 M
M

0
 0
0 

L
0 
O
M 

L 1 / x2, N 
L
[Estimador de mínimos cuadrados ponderados]
−1
 n
  n

β̂ = ∑ wi xi xi ' ∑ wi xi yi 
 i =1
  i =1

Donde wi =
1
.
x 22,i
Observaciones con varianza más pequeña tiene un peso mas elevada en la sumatoria y
así también en su influencia en el estimador.
Para ejemplo (2) se defina la matriz T para transformar el modelo.
0
1 / N1
 0
1/ N 2
Ω −1 = 
 M
M

0
 0
L
0 
L
0 
O
M 

L 1/ N R 
Recuerda que T ´T = Ω −1 .
1 /

T =



N1
0
0
1/ N2
M
0
M
0


L
0 
O
M 

L 1 / N R 
L
0
Para ejemplo (3) se defina la matriz T para transformar el modelo.
 N1
0
Ω −1 = 
M

0
0
N2
M
0
L 0 
L 0 
O M 

L NR 
Recuerda que T ´T = Ω −1 .


T =



N1
0
L
0
N2
L
M
0
M
0
O
L
0 

0 
M 

N R 
Perturbación desconocida:
1a etapa: Estimar los parámetros de la función de la varianza.
Estimar por MCO la regresión auxiliar ei2 = α 1 + α 2 x 2i + vi , donde ei representa los
residuos de la estimación MCO del modelo original, sin tener en cuenta la posible
ˆ −1 y también Tˆ .
heteroscedasticidad. El resultado de la regresión auxiliar defina Ω̂ , Ω
0
αˆ1 + αˆ 2 x2,1

αˆ1 + αˆ 2 x2, 2
0
ˆ =
Ω

M
M

0
0

L
0


L
0


O
M

L αˆ1 + αˆ 2 x2, N 
0
1 /(αˆ1 + αˆ 2 x2,1 )

0
1 /(αˆ1 + αˆ 2 x2, 2 )
ˆ −1 = 
Ω

M
M

0
0

L
0


L
0


O
M

L 1 /(αˆ1 + αˆ 2 x2, N )
1 / (αˆ1 + αˆ 2 x2,1 )
0

0
1 / (αˆ1 + αˆ 2 x2, 2 )

Tˆ = 
M
M


0
0


L
0


O
M

L 1 / (αˆ1 + αˆ 2 x2, N ) 
L
0
2a etapa: Aplica las formulas del estimador MCG, es decir estimar la relación
T̂y = T̂Xβ + T̂u por MCO.
yi
x2i
xki
ui
1
= β1
+ β2
+ ... + β k
+
αˆ1 + αˆ 2 x2i
αˆ1 + αˆ 2 x2i
αˆ1 + αˆ 2 x2,1
αˆ1 + αˆ 2 x2i
αˆ1 + αˆ 2 x2i
Matriz de varianza, covarianza robusto (White)
En algunos casos es difícil a priori efectuar supuestos para el comportamiento de la
función heteroscedástica. Es posible utilizar la estimación puntual MCO, corrigiendo la
estimación de su varianza.
var(βˆ MCO ) = σ 2 ( X ' X ) −1 X ' ΩX ( X ' X ) −1 =
1

N ( X ' X ) −1  σ 2 X ' ΩX ( X ' X ) −1
N

e12

0
1
1 2

X '
 σ X ' ΩX  se puede estimar a través de
N M
N


 0
0
e22
M
0
L 0

L 0
X.
O M 

L e N2 
donde [•] = σ u2 Ω y ei representan los residuos de la estimación MCO, y sus cuadrados
se utilizan para aproximar los elementos desconocidos para σ 2 Ω .