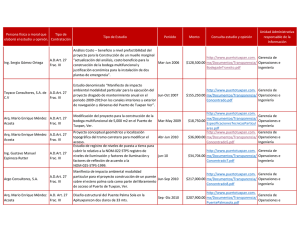
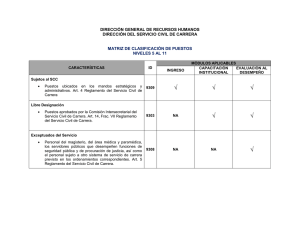
Diseño Instruccional Matemáticas. “Trigonometría y Geometría

Diseño Instruccional
Matemáticas. “Trigonometría y Geometría analítica”
Proyecto: Diseño e implementación de un programa para la actualización de
docentes de nivel medio superior en las áreas de físico-matemáticas y
ciencias naturales.
Responsable Técnico: Silvia Melbi Gaona Jiménez.
Supervisión y revisión del documento: Silvia Melbi Gaona Jiménez
Contenido
Temario ............................................................................................................................................... 2
Banco de preguntas........................................................................................................................... 62
Ejercicios............................................................................................................................................ 84
Vectores ........................................................................................................................................ 84
Puntos y rectas .............................................................................................................................. 87
Lugares geométricos I ................................................................................................................... 88
Lugares geométricos II .................................................................................................................. 89
Coordenadas Polares..................................................................................................................... 93
Ejercicios de Aplicación ................................................................................................................. 95
Tangentes a cónicas ...................................................................................................................... 97
Temario
 Examen Diagnostico
Módulo I.
Introducción
¡Bienvenidos a este curso de geometría analítica!
Éste no es un curso convencional de geometría analítica porque es un curso en línea o un curso
"virtual", como se le quiera llamar. Pero lo más importante es que en este curso se busca sacar
ventaja de que quien lo tome está conectado a Internet y por tanto tiene en sus manos la fuente
de información y autoaprendizaje más importante que ha creado el hombre. Entonces, su objetivo
principal no es enseñar la geometría analítica a personas que ya enseñan geometría analítica, sino
más bien, tomar como pretexto el enseñar cómo se hace geometría analítica usando vectores (un
método poco usado en las aulas), para mostrar una manera de incorporar la tecnología
informática en la práctica docente.
Es importante empezar el curso con una explicación de su estructura y funcionamiento. Se puede
decir que este curso virtual está diseñado en base a lecciones y evaluaciones semanales donde se
encuentran integrados contenidos explicativos sobre los temas y ejercicios de práctica
relacionados. En este caso una lección es una presentación estructurada de un tema con
contenidos y ejercicios. Dentro de los contenidos se encuentran las definiciones y explicaciones
necesarias junto con enlaces a documentos externos en conceptos claves. Estos enlaces se
encuentran como se muestra aquí en forma de hipervínculos. Al hacer "click" se despliegan y
permiten hacer revisiones más extensas del concepto en cuestión. Muchos de estos enlaces son a
la enciclopedia conocida como Wikipedia, que es un proyecto educativo muy importante a nivel
mundial , pues genera una enorme cantidad de información con un buen estándar de calidad. Los
artículos con mala estructura o información dudosa siempre presentan advertencias. Toda la
información contenida es de libre acceso y por eso es especialmente importante. Su intención es
transmitir cultura a la mayor cantidad de personas en el planeta, por eso es necesario que tanto
profesores como alumnos la conozcan y aprovechen.
También, dentro del contenido se encontrarán múltiples construcciones geométricas, útiles en un
curso como éste. Estas construcciones están diseñadas en una aplicación llamada "Geogebra"
(www.geogebra.org), otro programa de libre uso y distribución para fines no comerciales. El
Geogebra es una poderosa herramienta para la enseñanza de las matemáticas, puede usarse en
cualquier computadora personal y con cualquier sistema operativo. De hecho los invitamos a
instalarlo (http://www.geogebra.org/cms/es/installers) en sus propias computadoras personales
para usarlo durante este curso y como material en sus propios cursos.
El curso no requiere la instalación de geogebra, pues las lecciones son autocontenidas. Pero los
exhortamos a instalarlo y practicar su uso, la aplicación se puede considerar amable e intuitiva
2
pero si es necesario, el manual también puede encontrarse en línea. No vamos a hacer un curso de
geogebra aquí, pero sí es necesario presentar algunos puntos generales de su operación.
En la siguiente figura se observa una ventana de geogebra:
Podemos distinguir las partes importantes de la aplicación, que son: una barra de herramientas y
una barra de menú donde se encuentran todas las configuraciones y acciones a que se tiene
acceso como usuario; el área principal está dividida en dos partes, una que es el área gráfica
donde los dibujos aparecen y una ventana algebraica (panel derecho) donde se listan todos los
objetos de la construcción, pero en su definición abstracta, es decir, aparecen las ecuaciones y
coordenadas de los objetos dibujados. En la parte baja de la ventana hay una barra de entrada y
una lista de comandos, ahí se pueden capturar ecuaciones o funciones contenidas en la lista, que
sirven para hacer cálculos avanzados.
Noten algo importante, la figura que se muestra es interactiva, de hecho es el programa completo
ejecutándose dentro de este documento. Prueben a usarlo, con los botones en las barras se
pueden añadir puntos, vectores, líneas, curvas cónicas y muchas cosas más. Como primera
actividad practiquen a usarlo aquí mismo. También pueden capturar ecuaciones, por ejemplo en la
línea de entrada prueben teclear: "x^2+y^2=3" y chequen el dibujo.
3
En las lecciones encontrarán ventanas como ésta, pero mostrando sólo los componentes que
nosotros seleccionemos para la realizar la actividad en cuestión. Si se trata de una animación o
construcción automática busquen los botones de inicio dentro de la ventana gráfica que
usualmente muestran un triángulo. Debido a la interactividad de las construcciones este curso
está pensado para usarse de equipos conectados a internet con bandas anchas. Si la conexión es
lenta, la carga de las construcciones puede tomar tiempo, si éste es su caso, es necesario tener un
poco de paciencia.
La lección correspondiente a cada módulo es la actividad principal de éste . Se puede navegar en
ella cuantas veces se quiera, pero para hacer la evaluación correspondiente, es necesario
terminarla al menos una vez. Los ejercicios dentro de las lecciones se evalúan sólo como
mecanismo de retroalimentación. Si alguien decide terminar la lección sin realizar los ejercicios, no
tendrá ninguna retroalimentación. La calificación del módulo depende sólo del resultado del
examen correspondiente.
Esperamos que disfruten el curso, como nosotros hemos disfrutado su elaboración.
1.
Vectores
1.1. Definición de un vector y sus propiedades
Una buena manera de definir lo que es un vector es mediante la noción que
intuitivamente tenemos de una flecha. Es decir es una figura geométrica que
normalmente nos indica una dirección, pero que además tiene las siguientes propiedades:
1. Tiene un tamaño
2. Indica una dirección
3. Tiene un punto del cual comienza
Matemáticamente, los vectores son el conjunto de todas las flechas que podamos
imaginar. Así podemos pensar en flechas sobre una recta, en el plano, en el espacio y
hasta en hiperespacios. Aquí nos concentraremos en los que viven en un plano, ya que la
geometría analítica plana puede sacar mucha ventaja de estos.
En la siguiente figura tenemos un ejemplo interactivo que incluye algunos vectores en un
plano cartesiano. En este ejemplo es posible, usando el ratón, desplazar los vectores
libremente, sin que pierdan su forma (simplemente haz click con el botón izquierdo sobre
el centro del vector y mantenlo oprimido mientras lo trasladas). También es posible añadir
nuevos vectores utilizando la barra de entrada; por ejemplo tecleando el comando:
vector[(2,3),(1,-1)], se dibujará un vector que va del punto (2,3) al punto (1,-1).
4
Por esta propiedad se dice que los vectores son ``libres'' porque no importa donde se
coloquen siempre son iguales. Una vez colocados en un plano cartesiano un vector se
asocia inmediatamente con dos puntos del plano (por ejemplo el vector z se encuentra
asociado a los puntos G y H). Si cambio uno de los puntos el vector cambia su forma (se
puede probar en el ejemplo a hacerlo). Así se establece una especie de función entre
puntos y vectores. Para que esta función sea biyectiva, es decir que, haya una relación
única entre un punto y un vector es necesario trasladar a todos nuestro vectores a un
punto común, que podría ser al mismo tiempo el origen del plano cartesiano. El ejemplo
siguiente los dibuja así:
En el ejemplo anterior también es posible añadir más vectores centrados, tecleando en la
barra de entrada una letra minúscula y una coordenada de la siguiente manera: f=(4,2);
este comando que se dibujará el vector f del origen al punto (4,2).
Ahora se puede notar que los vectores perdieron libertad por estar atados al centro, pero
ganamos la posibilidad de matematizarlos, porque un vector ahora puede ser
representado por un punto en el plano y por tanto, usando ejes cartesianos, convertirlo en
un par de números ordenados (x,y). La importancia de esto radica en que ahora podemos
medir sus propiedades y definir operaciones entre ellos. Así para un vector u asociado a la
pareja (x,y) su tamaño se puede encontrar usando el \vert u\vert es el tamaño del vector
u, entonces
\begin{displaymath} \vert u\vert=\sqrt{x^2+y^2}. \end{displaymath}
5
(1)
Si quisiéramos saber el ángulo e inclinación del vector u, representado por \theta_u
entonces se tendría que echar mano de la trigonometría, usando la función tangente de
un triángulo rectángulo, de modo que es sencillo demostrar que:
\begin{displaymath} \theta_u=\arctan \frac{y}{x}. \end{displaymath}
(2)
Todo vector, esté donde esté, debe trasladarse al centro de los ejes cartesianos para
poderlo medir sus propiedades con las dos definiciones anteriores.
En la siguiente construcción se puede observar el tamaño y el ángulo de inclinación de un
vector, si se hace click en el punto B y se deja presionado el botón es posible cambiar el
vector u y sus propiedades se recalculan automáticamente. Es de notar que los vectores v
y w son vectores que apuntan en las direcciones de los ejes cartesianos sus tamaños
coinciden con las coordenadas x y y de u respectivamente formando siempre triángulos
rectángulos y por tanto relacionados con el teorema de Pitágoras y las funciones
trigonométricas.
1.2. Suma de vectores
Además de sus propiedades, también se pueden definir operaciones entre vectores. Así,
podemos definir la suma de vectores como: si tenemos dos vectores v y w descritos por
los puntos A=(x_1,y_1) y B=(x_2,y_2), la suma será:
v+w=(x_1+x_2,y_1+y_2).
(3)
En palabras, la suma de dos vectores es otro vector, tal que su abscisa es la suma de las
dos abscisas originales y su ordenada, la suma de las dos ordenadas. Al aplicar esta
definición y dibujarla, nos encontramos que se forma una figura como la siguiente:
6
Nótese que la suma de los vectores u y v es w y que el punto D donde llega el vector w es
siempre la suma por competentes de los puntos B y C (que a su vez representan las puntas
de los vectores u y v).
Si un vector tiene coordenadas (x,y) el vector (-x,-y), que le podríamos llamar su negativo,
es un flecha que apunta en la misma dirección, pero en sentido contrario. La resta de dos
vectores se puede definir por la suma de un vector por el negativo de otro. Es decir:
u-v=u+(-v)=(x_1 - x_2, y_1 - y_2 ) .
El vector que resulta de la resta de u y v, coincide siempre en tamaño y dirección con un
vector que va del punto (x_2,y_2) al punto (x_1,y_1).
Para terminar, un comentario sobre la suma y la resta en el Geogebra. Una vez capturado
un vector el Geogebra puede hacer las operaciones vectoriales usando la barra de entrada
de comandos. De esta manera, tenemos dos vectores capturados en u y v el comando:
u+v, calcula y dibuja el valor de la suma y el comando: u-v, la resta.
Hasta aquí con las definiciones asociadas a la suma, el flujo de la lección aquí permite las
siguientes opciones: Seguir con ejercicios de esta sección o continuar revisando
contenidos. La recomendación es hacer los ejercicios primero.
1.3. Productos vectoriales
La segunda operación importante es el producto por escalar. Si tenemos un vector
v=(x_1,y_1) y un escalar t el producto entre ambos se define como:
t v=(t x_1, t x_2).
Este producto tiene la característica de no alterar la dirección del vector y sólo cambiar su
tamaño. Se puede ver en el ejemplo siguiente esta característica, prueba la animación.
7
La última operación que definiremos es el producto escalar entre dos vectores. Cuando se
tienen dos vectores en el plano dados por v=(x_1,y_1) y u=(x_2,y_2) su producto escalar se
define como:
v \cdot u=x_1 x_2+y_1 y_2.
La primera implicación de esta definición es que si se toma el producto de un vector
u=(x,y) consigo mismo, es decir u \cdot u , el resultado coincide con la definición de su
tamaño, pero al cuadrado, es decir:
u \cdot u = x^2 + y^2 = |u|^2.
Ahora, observa la siguiente construcción, es un poco más elaborada, pero se explicará con
más detalle. En ella se puede notar que hay cuatro vectores u, v, w y z. El ángulo \alpha es
el ángulo entre u y v o entre w y z. El producto escalar de u y v se calcula automáticamente
y para comparar también se evalúa y se imprime la cantidad |u||v| \cos \alpha. Es
importante observar que ambas cantidades son iguales y si se cambia el tamaño de u o v
haciendo "click" y arrastrando cualquiera de sus puntas, siempre se conserva esa igualdad.
Por tanto, la construcción demuestra que la igualdad siguiente se cumple siempre:
u \cdot v = |u||v| \cos \alpha
También es importante remarcar que si el ángulo de inclinación entre ellos es un ángulo
recto entonces el producto punto es cero. En otras palabras, vectores perpendiculares
siempre tienen producto punto nulo. Es posible verificarlo en la misma construcción, de
modo que al mover el punto B o C hasta que los vectores sean perpendiculares sus
productos se hacen cero. Si los vectores fueran paralelos entonces su producto punto
sería igual al producto de sus magnitudes.
El segundo concepto importante que puede obtenerse de la figura anterior está
relacionado con los vectores w y z. El vector w se observa como una proyección del vector
v sobre el vector u. Además se puede observar que sin importar como se cambie u o v
siempre los tamaños de w y z son:
|w|=\frac{v \cdot u}{|u|},
8
|z|=\frac{v \cdot u}{|v|}.
Es decir, el tamaño de la proyección del vector v sobre el vector u es siempre el producto
punto de ambos entre el tamaño de u y viceversa, la proyección de u sobre v es el
producto puto de ambos entre v.
Dentro de una ventana de geogebra también es posible calcular los productos vectoriales.
Si se capturan un escalar t y dos vectores u y v, es posible hacer productos el producto por
escalar, por ejemplo con el comando: t*u, y el producto vectorial con la sintaxis u*v.
Cualquier producto se calcula con el símbolo "*" y el programa automáticamente
identifica si es un producto por escalar o un producto punto.
Las operaciones de suma, resta y multiplicación son las operaciones básicas entre vectores
y son suficientes para plantear una gran variedad de problemas geométricos.
1.4. Ejercicios
2. Cuestionario
Módulo II.
Puntos y Rectas
Un plano cartesiano es un sistema de referencia de un espacio de 2 dimensiones. Un punto es
cualquier ubicación sobre el plano cartesiano. Para describir la ubicación de un punto sobre el
plano cartesiano se utiliza el sistema de referencia del plano, conformado por 2 ejes \left(x,y\right)
y un origen. Los puntos también son conocidos como par ordenado, ya que la forma común de
representarlos es \left(n1,n2\right) donde cada uno de los números representa coordenadas en
cada uno de los ejes del plano.
Para representar un plano se utilizan 2 líneas, una horizontal y otra vertical que se cruzan de forma
perpendicular. Al punto exacto del cruce de los ejes se le llama origen y se representa con el par
ordenado \left(0,0\right). Los ejes forman 4 cuadrantes en los cuales se podrán ubicar puntos.
9
Relación punto-vector.
Si tenemos un punto A ubicado en (1,1) y lo movemos un punto a la izquierda y un punto arriba
vemos que ahora se ubica en (0,2). A este concepto se llama desplazamiento. Partiendo de este
concepto para representar la translación de un par ordenado en el plano, también podemos
llamar vector a un punto en el plano. Esto se representa con una flecha a la cual llamamos vector
geométrico.
Segmento: Distancia entre dos puntos.
Dado un punto A y un punto B, la recta comprendida entre ellos se llama segmento. Los puntos A y
B se llamaran extremos del segmento y la recta será conocida como segmento AB.
10
Recta.
En su definición más simple una recta es un conjunto infinito de puntos sobre un plano. Una recta
se puede definir de forma algebraica como
Ax+By+C=0
siempre que A o B sea diferente a 0.
Con base en un plano cartesiano podemos deducir que la unión de 2 vectores se le llama recta,
entiendo por vector a un par ordenado de coordenadas (x,y). Así podemos ver que una recta se
puede obtener mediante una ecuación vectorial.
Si tenemos que A=(4,4) y B=(3,1) son puntos que pasan por la recta a, podemos aplicar la siguiente
fórmula para determinar el vector sobre esa recta:
\nu=A-B=(5,4)-(2,1)=(3,3)
Ejemplo 1. Dados los puntos A=(2,2) y B=(1,-1) obtener el valor del vector AB. Usando la formula
anterior podemos ver que \nu=(1,3). Si a esto agregamos la representación geométrica ordinaria
de los vectores a y b que corresponden a los puntos A y B respectivamente obtenemos:
Ecuación paramétrica vectorial.
La ecuación paramétrica vectorial sirve para obtener puntos que pasen por una recta dada por 2
puntos. La ecuación es:
11
c = b + r (a-b)
Ejemplo 2. Obtener la ecuación paramétrica vectorial de la recta a que pasa por A=(-1,3) y B=(-5,2).
Para iniciar trazamos un diagrama con los puntos AB. Posteriormente obtenemos:
a-b=(-1,3)-(-5,-2)=(4,5)
Sustituyendo en la ecuación paramétrica vectorial obtenemos:
c=(-5,-2)+r(4,5)
Si restringimos el valor de r a un intervalo cerrado {r:a=r=b} entonces lo que obtenemos en la
gráfica es un segmento de recta que recorre desde B hasta A. Si r=0 entonces c=b, si r=1 entonces
c=A. Si queremos un resultado menor a b entonces r<0 y si queremos un resultado mayor a a
entonces r>1.
1.
División de segmentos en una razón dada
Una razón es una división o fracción, por ejemplo AC/CB es una razón. Estas razones se usan
para determinar las proporciones de un objeto. ¿Qué significa la división de un segmento en
una razón dada? Significa medir el segmento y partirlo, y las medidas de cada pedazo de
segmento, al dividirlas, tienen que dar igual a la razón que buscamos.
Con estos conceptos partiremos para encontrar las ecuaciones que nos permitan encontrar un
punto sobre el segmento. Analicemos primero el escenario de forma análoga, teniendo
A(x1,y1) y B(x2,y2) y asumiendo que r=AC/CB podemos enfocarnos en obtener x.
NOTA: El orden en el cual nos dan un segmento es importante, así que debemos de poner
especial atención en este punto.
r=\frac{AC}{CB}=\frac{x1-x}{x-x2}
r(x-x2)=x1-x
12
rx-rx2=x1-x
rx+x=x1+rx2, factorizando obtenemos
x(r+1)=x1+rx2
x=\frac{x1+rx2}{1+r}
El mismo procedimiento lo enfocamos para obtener y:
y=\frac{y1+ry2}{1+r}
Nota: Si r es un valor negativo entendamos que este se encuentra fuera del segmento dado. Si
r es un valor positivo se encuentra dentro del segmento.
2.
Pendiente de una recta
Una recta se puede describir considerando un vector w que tiene la misma dirección que la
recta, y un punto de inicio del vector. El caso más sencillo es considerar un vector w , y como
punto inicial el origen. El vector con punto inicial en el origen se puede expresar como w=(h,k).
En la siguiente figura se observa que el vector w forma un ángulo \theta con el eje x. Al utilizar
esta geometría se define la pendiente de una recta L como:
m=Tan\:\theta=\frac{k}{h},
En caso de que h=1, entonces, m=Tan\:\theta=k,
Una recta L que no intercepta al origen, y contiene a los puntos A(x_1,y_1) y B(x_2,y_2), se
puede representar vectorialmente que se muestra en la siguiente figura. Ahí se puede ver que,
del origen C al punto A se tiene al vector u, y del origen C al punto B se tiene al vector v, y por
lo tanto, el vector diferencia es w=v-u, el cual respecto a las coordenadas se puede expresar
13
como w=(x_2-x_1,y_2-y_1). Utilizando la definición de pendiente aplicada a este caso se tiene
que:
m=Tan\:\theta=\frac{y_2-y_1}{x_2-x_1},
En la figura se representa la pendiente como:
m=Tan\:\theta=\frac{k}{h}=\frac{\frac{y_2-y_1}{x_2-x_1}}{1},
es decir,
h=1, y m=Tan\:\theta=k=\frac{y_2-y_1}{x_2-x_1},
3.
Ángulo entre dos rectas
En la siguiente figura se muestran dos rectas L_1 y L_2, que se interceptan en el punto E. La
intercepción forma cuatro vértices, y el vértice superior de la intercepción tiene un ángulo
\theta, que es considerado el ángulo entre las rectas. El ángulo \theta que se forma en la
intersección de las rectas, cumple por la geometría que \theta=\alpha-\beta, por lo tanto, se
tiene que Tan\:\theta=Tan(\alpha-\beta), y al usar la identidad trigonométrica para la
tangente de la diferencia de dos ángulos se tiene que:
Tan\:\theta=Tan(\alpha-\beta)=\frac{Tan\:\alphaTan\:\beta}{1+(Tan\:\alpha)(Tan\:\beta)}=\frac{m_2-m_1}{1+m_1m_2}
En esta relación se ha considerado que, la pendiente de la recta L_2 es m_2=Tan\:\beta, y la
pendiente de la recta L_1 es m_1=Tan\:\alpha.
14
Por otro lado, también se puede relacionar el ángulo entre dos rectas, al considerar los
vectores v y w, y al utilizar la relación del producto punto con el Cos\:\theta, se obtiene que:
Cos\:\theta=\frac{v\cdot w}{\left\|v\right\|\left\|w\right\|}
4.
Rectas paralelas
Sabemos de geometría elemental euclidiana que dos rectas en el plano son paralelas si no se
cortan en ningún punto. Esto quiere decir, las rectas tienen iguales ángulos que cortan el eje x,
es decir, \alpha=\beta. Por lo tanto, \theta=0^{\circ}. Al considerar esto en la relación
Tan\:\theta, se tiene que,
Tan\:\theta=0=\frac{m_2-m_1}{1+m_1m_2}
Es decir, m_1=m_2. Por lo tanto, dos rectas paralelas tienen igual pendiente. También, el
ángulo \theta entre dos rectas paralelas se puede encontrar al considerar la relación del
coseno de \theta, evaluado cuando, \theta=0^{\circ}, o bien, \theta=180^{\circ}. Al considerar
15
que el vector v es contenido en la recta L_1, y el vector w está contenido en la recta L_2,
entonces, al aplicarse los dos valores al ángulo \theta, se encuentra que,
\frac{v\cdot w}{\left\|v\right\|\left\|w\right\|}=\pm1
El signo "+" corresponde a \theta=0^{\circ}, y el signo "-" corresponde a theta=180^{\circ}.
Ésta es la relación que resume la condición de paralelismo entre dos rectas, cuando se
conocen un vector contenido en cada una de las rectas.
5.
Rectas perpendiculares
Dos rectas son perpendiculares si forman éstas un ángulo \theta=90^\circ al interceptarse.
Para obtener la condición de las pendientes de dos rectas perpendiculares, se considerará la
función inversa de la reciproca de la tangente, es decir la cotangente. Sabemos que,
Cot\:\theta=\frac{1}{Tan\:\theta},
Al aplicar la relación de Tan\:\theta con respecto a las pendientes de las rectas se obtiene:
Cot\:\theta=\frac{1+m_1m_2}{m_2-m_1}
Al aplicar en la función cotangente, \theta=90^\circ, se tiene que,
Cot\:90^\circ=0=\frac{1+m_1m_2}{m_2-m_1}
Por lo tanto, cuando dos rectas son perpendiculares sus pendientes cumplen la relación,
m_1m_2=-1.
Al considerar que el vector v es contenido en la recta L_1, y el vector w está contenido en la
recta L_2, entonces, al aplicarse que \theta=90^\circ en la relación del Cos\:\theta, y se
encuentra que,
Cos\:90^\circ=0=\frac{v\cdot w}{\left\|v\right\|\left\|w\right\|}
Es decir, v\cdot w=0, que es la condición de perpendicularidad de dos rectas, o bien, de los dos
vectores contenidos en cada una de las rectas.
6.
Ecuaciones de la recta
La recta puede describirse analíticamente con diferentes expresiones, se iniciará con la
descripción paramétrica de ésta.
16
Para describir la recta en forma paramétrica se considera que la recta contiene al vector
u=(h,k), y que este vector inicia en el punto P_0 (x_0,y_0). Cualquier punto en la recta se
representa
como
P(x,y).
Con
este
punto
se
obtiene
el
vector
\stackrel{\rightarrow}{PP_0}=v=(x-x_0,y-y_0), y dado que los vectores u y v pertenecen a la
recta, entonces son paralelos, por lo tanto, deben cumplir que, v=ru, donde \infty\leqr\leq\infty. Aplicando la condición vectorial se tiene que:
x-x_0=rh,
y-y_0=rk,
y al realizar un poco de álgebra se obtiene:
x=x_0+rh,
y=y_0+rk.
Estas dos ecuaciones son las que describen perimétricamente a cualquier punto de la recta L.
7.
Expresión de la recta en forma general
La recta se expresa comúnmente en forma general como, Ax+By+C=0. La forma general puede
relacionarse con la forma paramétrica al observar que, r=\frac{x-x_0}{h}=\frac{y-y_0}{k},
de donde se puede realizar un poco de álgebra hasta obtener que:
kx-hy+(hy_0-kx_0)=0
Al comparar la forma general con la ecuación anterior se observa que,
A=k;\ B=-h;\ C=hy_0-kx_0.
8.
Recta que pasa por dos puntos
17
Cuando una recta pasa por dos puntos, se genera la geometría que se muestra en la figura
siguiente. Al considerar que la recta pasa por los puntos P_1(x_1,y_1) y P_2(x_2,y_2),
entonces si se considera un punto P(x,y) de la recta, el vector u y v se expresan como:
u=(x_2-x_1,y_2-y_1 );\ v=(x-x_1,y-y_1);
Por lo tanto, la pendiente de la recta considerando ambos vectores es:
m_L=\frac{y-y_1}{x-x_1}=\frac{y_2-y_1}{x_2-x_1},
y al realizar un poco de álgebra se obtiene:
y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)
9.
Ecuación de la recta al considerar la pendiente y un punto
En caso de que sea conocida la pendiente de la recta y un punto, la ecuación de la recta se
puede obtener al considerar la figura siguiente, si observamos que, cualquier punto P(x,y)
genera un vector w con el punto P_1(x_1,y_1) como:
\stackrel{\rightarrow}{P_1P}=\stackrel{\rightarrow}{u}=(x-x_1,y-y_1),
Por lo tanto, la pendiente se encuentra como:
m_L=\frac{y-y_1}{x-x_1},
a partir esta ecuación se obtiene que:
y-y_1=m_L(x-x_1).
Esta ecuación es la ecuación buscada que describe la recta.
18
10. Ecuación de la recta al considerar la pendiente y la ordena al origen
Un caso particular de la ecuación de pendiente-punto es la aplicación cuando el punto es el
cruce de la recta con el eje y, considerando el punto como P_1(0,b), y a la pendiente se le
considera m_L=m, con lo cual, la ecuación de la recta es:
y-b=m(x-0),
lo cual es común expresar como:
y=m_ x+b.
La gráfica de este caso se puede ver en la figura siguiente.
Una correspondencia entre expresiones entre la expresión general de la recta y la expresión
de ordenada al origen se puede realizar al iniciar con la expresión general Ax+By+C=0, después
de realizar un poco de álgebra se obtiene que:
y=-\frac{A}{B}x+(-\frac{C}{B}),
19
Por lo tanto, por comparación entre coeficientes se obtiene que:
m=-\frac{A}{B};\ b=-\frac{C}{B}.
11. Ecuación de la recta en forma simétrica
La ecuación de la recta que en forma simétrica considera que la recta intercepta a los ejes x y
y, como se muestra en la siguiente figura.
Al considerar la ecuación para la recta a la que pertenecen dos puntos, P_1(a,0) y P_2(0,b), se
obtiene el siguiente desarrollo:
y-0=\frac{b-0}{0-a}(x-a),
-ay=bx-ab,
bx+ay=ab,
\frac{x}{a}+\frac{y}{b}=1.
La relación,
\frac{x}{a}+\frac{y}{b}=1,
es la expresión analítica de la recta en forma simétrica.
12. Distancia punto recta
Toda recta L se puede visualizar como una sucesión de puntos P(x,y), los cuales satisfacen la
ecuación,
Ax+By+C=0,
o bien, la ecuación,
y=mx+b,
donde se ha considerado,
20
m=-\frac{A}{B};\:\:b=-\frac{C}{B}.
Un punto exterior a una recta, tiene una distancia a cualquier punto P(x,y) de una recta.
Aunque, la distancia d se define como, “La distancia mínima de un punto P_e(x_e,y_e) exterior
a un punto P(x,y), es decir, la distancia d mínima del segmento \overline{PP_e}.
Para deducir la ecuación con la que se evalúa d, se ha construido la geometría de la figura.
Para deducir la ecuación que evalúa la distancia d se supondrá que los datos conocidos son, la
ecuación de la recta en la forma, y=mx+b, y el punto externo P_e(x_e,y_e). Para obtener la
distancia d se requiere un punto conocido, y un vector normal unitario. Como punto conocido
se usa al punto de la recta que tiene como valor en las abscisas a x=x_e, por lo tanto, el punto
conocido es, P_v(x_e,y(x_e)), por lo tanto, el vector V es,
V=(x_e-x_e,y_e-y(x_e ))=(0,y_e-mx_e-b),
donde se ha usado que la ecuación de la recta es y=mx+b, de donde, y(x_e) es,
y(x_e)=mx_e+b. Ahora un vector que es paralelo a la recta es el vector T=(1,m), por lo tanto,
un vector normal a este vector es N=(-m,1). Esto se infiere de la condición de
perpendicularidad que cumple T\circN=0, lo cual se puede verificar para nuestros vectores.
Utilizando estos vectores la distancia d es la componente del vector V sobre el vector normal
unitario, que es.
\widehat{N}=\frac{N}{\left\|N\right\|}.
Con esto, la distancia d se obtiene por,
d=\left|V\cdot\widehat{N}\right|=\left|V\cdot\left(\frac{N}{\left\|N\right\|}\right)\right|=\le
ft|\frac{V\cdot
N}{\left\|N\right\|}\right|=\frac{\left|V\cdot
N\right|}{\left|\left\|N\right\|\right|}.
d=\frac{\left|\left(0,y_e-mx_e-b\right)\left(m,1\right)\right|}{\left|\sqrt{1+m^2}\right|}=\frac{\left|y_e-mx_eb\right|}{\left|\sqrt{1+m^2}\right|},
21
d=\frac{\left|y_e-mx_e-b\right|}{\sqrt{1+m^2}}.
Solo para remarcar, la distancia se evaluará por,
d=\displaystyle{\frac{\left|y_e-mx_e-b\right|}{\sqrt{1+m^2}}}.
Si analizamos la relación vemos que, se utilizan los valores del punto externo x_e y y_e, y de la
ecuación de la recta se utilizan los parámetros, m y b.
En la literatura es más común utilizar la ecuación de la recta en forma general, por lo tanto, se
obtendrá una expresión para obtener la distancia considerando esa ecuación.
Recordemos que si se tiene la ecuación general de la recta en la forma, Ax+By+C=0, la
pendiente y ordenada al origen se relacionan por:
m=-\frac{A}{B};\:\:b=-\frac{C}{B},
valores que se sustituyen en la relación de la distancia d, y se obtiene,
d=\frac{\left|y_e-mx_e-b\right|}{\sqrt{1+m^2}}=\frac{\left|y_e-\left(-\frac{A}{B}\right)x_e\left(-\frac{C}{B}\right)\right|}{\sqrt{1+\left(-\frac{A}{B}\right)^2}}=\frac{\left|\frac{B}{B}y_e\left(-\frac{A}{B}\right)x_e-\left(-\frac{C}{B}\right)\right|}{\sqrt{\frac{A^2+B^2}{B^2}},
d=\frac{\frac{1}{\left|B\right|}\left|By_e+Ax_e+C\right|}{\frac{1}{\left|B\right|}\sqrt{A^2+B^
2}},
d=\frac{\left|By_e+Ax_e+C\right|}{\sqrt{A^2+B^2}}.
Esta ecuación se puede reescribir como,
d=\displaystyle{\frac{\left|Ax_e+By_e+C\right|}{\sqrt{A^2+B^2}}}.
Ésta última relación utiliza la ecuación general de la recta donde se le sustituyen los valores de
las coordenadas externas, y se utilizan los coeficientes A y B de la misma ecuación general de
la recta.
13. Bisectriz
La recta bisectriz L_b de un ángulo, lo divide en dos partes iguales. Además se caracteriza
porque cualquier punto de esta recta tiene la misma distancia en valor absoluto con la recta
superior e inferior, como se muestra en la figura siguiente. Debemos aclarar que cuando un
punto está por debajo de la recta, la distancia resulta negativa, y es la función valor absoluto lo
que nos genera el valor positivo. Cuando el punto está arriba de la recta la distancia resulta
positiva. Por lo tanto, esto aplicado a la bisectriz, en la figura nos da la condición de la
distancia del punto P(x,y) de la recta bisectriz a cada recta del ángulo, cuando las ecuaciones
de las rectas L y L' están expresadas en la forma general, se tiene que,
22
d_2=-d_1,
Es decir,
\displaystyle{\frac{Ax+By+C}{\sqrt{A^2+B^2}}=-\frac{A'x+B'y+C'}{\sqrt{(A')^2+(B')^2}}},
si se definen como,
\displaystyle{\vartheta=\sqrt{A^2+B^2}},
\displaystyle{\vartheta'=\sqrt{(A')^2+(B')^2}},
la ecuación de la recta se expresa como,
(\vartheta'A+\vartheta A')x+(\vartheta'B+\vartheta B')y+(\vartheta'C+\vartheta C')=0.
que es la ecuación que describe a la recta bisectriz.
14. Intercepción entre dos rectas
Dos rectas no paralelas se interceptan en un punto P_0(x_0,y_0). Éste se encuentra al resolver
de forma simultánea las ecuaciones de las rectas L_1 y L_2, que son:
A_1x+B_1y=C_1,
A_2x+B_2y=C_2.
Dado que el punto pertenece a ambas rectas, debe ser solución del sistema, es decir, se debe
cumplir que,
A_1x_0+B_1y_0=C_1,
A_2x_0+B_2y_0=C_2.
Existen varios procedimientos para encontrar x_0 y y_0, no obstante, nosotros para obtener
estos usaremos las siguientes ecuaciones:
\displaystyle{x_0=\frac{C_1B_2-C_2B_1}{A_1B_2-A_2B_1}},
\displaystyle{y_0=\frac{C_2A_1-C_1A_2}{A_1B_2-A_2B_1}}.
23
De esta forma se obtiene el punto de intercepción P_0(x_0,y_0).
15. Propiedades de los triángulos
Un triángulo es una figura geométrica que se forma por la intercepción de tres segmentos
continuos de rectas, como se muestra en la figura siguiente. Debido a su forma el triángulo
tiene también tres ángulos.
El triángulo es una figura geométrica que ha sido estudiada ampliamente, y es común que en
geometría analítica se le describa considerando que son conocidos los puntos de sus vértices.
Luego, a partir de esta información se obtienen los parámetros y ecuaciones de las rectas
características de esta figura. Los elementos que se describen son, las ecuaciones de las rectas
que contienen a los segmentos que forman el triángulo, la ubicación de los vértices, los valores
de los ángulos, las ecuaciones de las bisectrices, las ecuaciones de las medianas, las
ecuaciones de las mediatrices, el punto de intercepción de las bisectrices, el punto de
intercepción de las mediatrices, el punto de intercepción de las medianas, el punto de
intercepción de las alturas, el área y el perímetro del triángulo.
16. Longitudes de los lados del triángulo
Las longitudes d_A, d_B y d_C de los lados de un triángulo, al aplicar la relación para obtener
la distancia entre dos puntos, con los puntos que se muestran en la figura, se obtienen como:
d_A=\sqrt{(x_3-x_2)^2+(y_3-y_2)^2}
d_B=\sqrt{(x_3-x_1)^2+(y_3-y_1)^2}
d_C=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
17. Pendientes de las rectas que contienen a los segmentos del triángulo
24
Las pendientes de las rectas que contienen los segmentos \overline{AB}, \overline{BC} y
\overline{AC} se evalúan usando la ecuación para la pendiente que considera el vector entre
los dos puntos de cada segmento, con esto las pendientes se evalúan como,
\displaystyle{m_{AB}=\frac{y_2-y_1}{x_2-x_1}},
\displaystyle{m_{BC}=\frac{y_3-y_2}{x_3-x_2}},
\displaystyle{m_{AC}=\frac{y_1-y_3}{x_1-x_3}}.
18. Propiedades de los triángulos
El ángulo de los vértices se evalúa considerando la relación para calcular el ángulo entre dos
rectas. Una consideración que se debe hacer es, tomar como recta 2 de la ecuación a la que
tiene mayor ángulo, al medir éste en sentido contrario a las manecillas del reloj, por supuesto,
la recta 1 será la que tiene menor ángulo con la misma consideración.
\displaystyle{\theta_A=Tan^{-1}\left(\frac{m_{AC}-m_{AB}}{1+m_{AB}m_{AC}}\right)},
\displaystyle{\theta_B=Tan^{-1}\left(\frac{m_{AB}-m_{BC}}{1+m_{AB}m_{BC}}\right)},
\displaystyle{\theta_C=Tan^{-1}\left(\frac{m_{BC}-m_{AC}}{1+m_{BC}m_{AC}}\right)}.
19. Ecuaciones de las rectas que contienen los segmentos del triángulo
Para encontrar las ecuaciones de las rectas que contienen a los segmentos que forman un
triángulo se usará la ecuación de la recta que considera dos puntos, por lo tanto, para el
segmento \overline{AB} pertenece a la recta que se describe por,
\displaystyle{y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right)}.
El segmento \overline{AC} pertenece a la recta que se describe por,
\displaystyle{y-y_1=\frac{y_3-y_1}{x_3-x_1}\left(x-x_1\right)}.
El segmento \overline{BC} pertenece a la recta que se describe por,
\displaystyle{y-y_2=\frac{y_3-y_2}{x_3-x_2}\left(x-x_2\right)}.
20. Ecuaciones de las bisectrices de un triángulo
La bisectriz de un ángulo es la recta que lo divide en dos partes iguales. Por lo tanto, un
triángulo tiene tres bisectrices, una para cada ángulo. Las tres bisectrices de los ángulos
internos de un triángulo se cortan en un único punto, que equidista de los lados. A este punto
se le denomina “incentro” del triángulo y este punto tiene como característica geométrica, de
ser el centro de una circunferencia inscrita dentro del triángulo. Por lo tanto, esta
circunferencia es tangente a cada uno de los lados del triángulo.
25
Las coordenadas del incentro son una combinación de las coordenadas de sus vértices y las
longitudes de sus lados. Si los vértices tienen coordenadas A(x_1,y_1), B(x_2,y_2) y C(x_3,y_3)
y sus lados opuestos tienen las longitudes d_A, d_B y d_C, entonces el incentro se obtiene por
medio de la ecuación:
\displaystyle{I\left(\frac{d_Ax_1+d_Bx_2+d_Cx_3}{d_A+d_B+d_C},\frac{d_Ay_1+d_By_2+d_Cy
_3}{d_A+d_B+d_C}\right)=I\left(x_1,y_1\right)}
Es decir,
\displaystyle{x_1=\frac{d_Ax_1+d_Bx_2+d_Cx_3}{d_A+d_B+d_C}},
\displaystyle{y_1=\frac{d_Ay_1+d_By_2+d_Cy_3}{d_A+d_B+d_C}}.
Una vez que conocemos el incentro nos podemos ayudar con este punto para obtener las
ecuaciones de las bisectrices. Dado que el incentro pertenece a las tres bisectrices, se puede
usar este punto para obtener la ecuación de la bisectriz, al considerar que la bisectriz contiene
al vértice y el incentro. A partir de esto, la bisectriz del ángulo del punto A se obtiene como,
\displaystyle{y-y_I=\frac{y_1-y_I}{x_1-x_I}\left(x_x_I\right)},
la bisectriz del ángulo del punto B se obtiene como,
\displaystyle{y-y_I=\frac{y_2-y_I}{x_2-x_I}\left(x_x_I\right)},
la bisectriz del ángulo del punto C se obtiene como,
\displaystyle{y-y_I=\frac{y_3-y_I}{x_3-x_I}\left(x_x_I\right)},
Los segmentos de las bisectrices, el incentro, y la circunferencia inscrita en el triángulo se
muestran en la siguiente figura.
26
21. Medianas del triángulo
Las medianas como se muestra en la siguiente figura, son las tres rectas que unen cada vértice
del triángulo con el centro del lado opuesto. Las tres medianas se cortan en un único punto (G
en la figura siguiente) llamado centro de gravedad o centro de masa del triángulo.
Los puntos medios se encuentran por las ecuaciones que considera que un segmento se divide
en dos partes iguales, por lo tanto, para el punto D se tiene,
\displaystyle{x_{AB}=\frac{x_1+x_2}{2}},
\displaystyle{y_{AB}=\frac{y_1+y_2}{2}}.
para el punto E se tiene,
\displaystyle{x_{BC}=\frac{x_2+x_3}{2}},
\displaystyle{y_{BC}=\frac{y_2+y_3}{2}}.
para el punto F se tiene,
\displaystyle{x_{AB}=\frac{x_1+x_2}{2}},
\displaystyle{y_{AB}=\frac{y_1+y_2}{2}}.
Al utilizar estos puntos se encuentran las ecuaciones de las rectas, con el uso de la ecuación de
la recta que considera dos puntos conocidos, así el segmento \overline{AE} está contenida en
la recta,
\displaystyle{y-y_1=\frac{y_{BC}-y_1}{x_{BC}-x_1}\left(x-x_1\right)}.
el segmento \overline{BF} está contenida en la recta,
\displaystyle{y-y_2=\frac{y_{AC}-y_2}{x_{AC}-x_2}\left(x-x_2\right)}
el segmento \overline{CD} está contenida en la recta,
27
\displaystyle{y-y_3=\frac{y_{AB}-y_3}{x_{AB}-x_3}\left(x-x_3\right)}
El punto G, se obtiene por la solución simultánea de dos de las ecuaciones para los segmentos
\overline{AE}, \overline{BF} y \overline{CD}.
22. Mediatrices
La mediatriz de un segmento es la recta perpendicular a dicho segmento trazada a partir de su
punto medio. Por la propiedad antes mencionada, en todo triángulo ABC como se muestra en
la siguiente figura, las mediatrices de sus tres lados concurren en un mismo punto, llamado el
circuncentro del triángulo (punto O en la figura). Dicho punto equidista de los vértices del
triángulo. La circunferencia del centro O y de radio OA, pasa por los otros dos vértices del
triángulo. Se dice que dicha circunferencia es circunscrita al triángulo y que el triángulo está
inscrito en la circunferencia.
Las ecuaciones de las mediatrices se deducen al saber que son perpendiculares al segmento
en el punto medio, esta condición nos hace inferir que la recta M_{AB} tiene pendiente que
cumple, (m_{AB})m_{AB\bot}=-1, dado que,
\displaystyle{m_{AB}=\frac{y_2-y_1}{x_2-x_1}},
entonces,
\displaystyle{m_{AB\bot}=-\frac{x_2-x_1}{y_2-y_1}}
El punto medio D es,
28
\displaystyle{x_{AB}=\frac{x_1+x_2}{2}},
\displaystyle{y_{AB}=\frac{y_1+y_2}{2}}.
Utilizando esto, la ecuación de la mediatriz M_{AB} es,
\displaystyle{y-\left(\frac{y_1+y_2}{2}\right)=-\frac{x_2+x_1}{y_2-y_1}\left(x\left(\frac{x_1+x_2}{2}\right)\right)}.
La recta M_{BC} tiene pendiente que cumple, (m_{BC})m_{bc\bot}=-1 dado que,
\displaystyle{m_{BC}=\frac{y_3-y_2}{x_3-x_2}},
entonces,
\displaystyle{m_{BC\bot}=-\frac{x_3-x_2}{y_3-y_2}}.
El punto medio E es,
\displaystyle{x_{BC}=\frac{x_2+x_3}{2}},
\displaystyle{y_{BC}=\frac{y_2+y_3}{2}}.
Utilizando esto, la ecuación de la mediatriz M_{BC} es,
\displaystyle{y-\left(\frac{y_2+y_3}{2}\right)=-\frac{x_3-x_2}{y_3-y_2}\left(x\left(\frac{x_2+x_3}{2}\right)\right)}.
La recta M_{AC} tiene pendiente que cumple, (m_{AC})m_{AC\bot}=-1 dado que,
\displaystyle{m_{AC}=\frac{y_1-y_3}{x_1-x_3}},
entonces,
\displaystyle{m_{AC\bot}=-\frac{x_1-x_3}{y_1-y_3}}.
El punto medio F es,
\displaystyle{x_{AC}=\frac{x_1+x_3}{2}},
\displaystyle{y_{AC}=\frac{y_1+y_3}{2}}.
Utilizando esto, la ecuación de la mediatriz M_{AC} es,
\displaystyle{y-\left(\frac{y_1+y_3}{2}\right)=-\frac{x_1-x_3}{y_1-y_3}\left(x\left(\frac{x_1+x_3}{2}\right)\right)}.
El punto 0(h,k) se encuentra por la solución simultánea de dos de las tres ecuaciones de las
mediatrices, M_{AB}, M_{BC} y M_{AC}.
29
23. Alturas de un triángulo
La altura de un triángulo con respecto de un lado del triángulo, es la distancia más corta entre
la recta que contiene al lado y el vértice opuesto. Por lo tanto, un triángulo tiene tres alturas
que en la figura h_A, h_B y h_C. Las alturas se interceptan en un punto llamado ortocentro
que en la figura se muestra por H. Debemos comentar que en todo triángulo, al menos una de
las alturas se encuentra dentro del triángulo, y que la altura de mayor longitud es la
correspondiente al lado menor del triángulo.
Para obtener la ecuación de la recta que contiene a “la altura” se tiene que considerar el
punto vértice de donde se genera la altura y la pendiente de la recta que contiene a la altura,
al saber que es perpendicular a la recta que contiene al segmento del lado del triángulo
opuesto al vértice. Para el caso de nuestra figura, la recta H_A, el punto vértice es A(x_1,y_1),
y la pendiente es,
\displaystyle{m_{BC\bot}=-\frac{x_3-x_2}{y_3-y_2}},
con esto, la ecuación de la recta que contiene a esta altura es,
\displaystyle{y-y_1=-\frac{x_3-x_2}{y_3-y_2}\left(x-x_1\right)}.
Para encontrar la longitud de la altura se considera la ecuación de la recta del segmento
contrario al vértice y en esta ecuación se aplica las coordenadas del vértice como se mostró en
la fórmula de la distancia de un punto a una recta. En este caso, la ecuación de la recta del
segmento \overline{BC} es,
\displaystyle{y-y_2=-\frac{y_3-y_2}{x_3-x_2}\left(x-x_2\right)},
30
o bien,
\left(y_3-y_2\right)x-\left(x_3-x_2\right)y+\left(x_3-x_2\right)y_2-\left(y_3-y_2\right)x_2=0,
al considerar esta ecuación la altura se obtiene como,
\displaystyle{h_A=\frac{\left|\left(y_3-y_2\right)x_1-\left(x_3-x_2\right)y_1+\left(x_3x_2\right)y_2-\left(y_3-y_2\right)x_2\right|}{\sqrt{\left(y_3-y_2\right)^2+\left(x_3x_2\right)^2}}},
La recta H_C, el punto vértice es C(x_3,y_3), y la pendiente es,
\displaystyle{m_{AB\bot}=-\frac{x_2-x_1}{y_2-y_1}},
con esto, la ecuación de la recta que contiene a esta altura H_C es,
\displaystyle{y-y_1=-\frac{x_2-x_1}{y_2-y_1}\left(x-x_3\right)}.
Para encontrar la altura h_C se considera la ecuación de la recta del segmento contrario al
vértice C, y en esta ecuación se aplica las coordenadas de este vértice, como fue mostrado en
la fórmula de la distancia de un punto a una recta. En este caso, la ecuación de la recta del
segmento \overline{AB} es,
\displaystyle{y-y_1=-\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right)}
o bien,
\left(y_2-y_1\right)x-\left(x_2-x_1\right)y+\left(x_2-x_1\right)y_1-\left(y_2-y_1\right)x_1=0,
al considerar esta ecuación la altura h_C se obtiene como,
\displaystyle{h_C=\frac{\left|\left(y_2-y_1\right)x_2-\left(x_2-x_1\right)y_3+\left(x_2x_1\right)y_1-\left(y_2-y_1\right)x_1\right|}{\sqrt{\left(y_2-y_1\right)^2+\left(x_2x_1\right)^2}}}.
La recta H_B, el punto vértice es B(x_2,y_2), y la pendiente es,
\displaystyle{m_{AC\bot}=-\frac{x_1-x_3}{y_1-y_3}},
con esto, la ecuación de la recta que contiene a esta altura H_B es,
\displaystyle{y-y_2=-\frac{x_1-x_3}{y_1-y_3}\left(x-x_2\right)}.
Para encontrar la altura h_B se considera la ecuación de la recta del segmento contrario al
vértice B(x_2,y_2), y en esta ecuación se aplica las coordenadas de este vértice, como fue
mostrado en la fórmula de la distancia de un punto a una recta. En este caso, la ecuación de la
recta del segmento \overline{AC} es,
31
\displaystyle{y-y_1=-\frac{y_3-y_1}{x_3-x_1}\left(x-x_1\right)}
o bien,
\left(y_3-y_1\right)x-\left(x_3-x_1\right)y+\left(x_3-x_1\right)y_1-\left(y_3-y_1\right)x_1=0,
al considerar esta ecuación la altura se obtiene como,
\displaystyle{h_B=\frac{\left|\left(y_3-y_1\right)x_2-\left(x_3-x_1\right)y_2+\left(x_3x_1\right)y_1-\left(y_3-y_1\right)x_1\right|}{\sqrt{\left(y_3-y_1\right)^2+\left(x_3x_1\right)^2}}}.
La intercepción de las alturas se puede obtener por la solución simultánea de dos de las tres
ecuaciones de las rectas H_A, H_B y H_C.
Debemos comentar que en un triángulo equilátero, las medianas coinciden con las mediatrices
de los lados, con las alturas del triángulo, y con las bisectrices de los tres ángulos.
24. El perímetro y el área del triángulo
El perímetro de un triángulo es la suma de las longitudes de sus lados. Por lo tanto, es,
P=d_A+d_B+d_C.
El área de un triángulo se encuentra por la conocida fórmula,
\displaystyle{A=\frac{b \cdot h}{2}},
en este caso, puede ser,
\displaystyle{A=\frac{d_Ah_A}{2}},
\displaystyle{A=\frac{\left(\sqrt{\left(x_3-x_2\right)^2+\left(y_3y_2\right)^2}\right)\left(\frac{\left|\left(y_3-y_2\right)x_1-\left(x_3-x_2\right)y_1+\left(x_3x_2\right)y_2-\left(y_3-y_2\right)x_2\right|}{\sqrt{\left(x_3-x_2\right)^2+\left(y_3y_2\right)^2}}\right)}{2}},
\displaystyle{A=\frac{\left|\left(y_3-y_2\right)x_1-\left(x_3-x_2\right)y_1+\left(x_3x_2\right)y_2-\left(y_3-y_2\right)x_2\right|}{2}}.
O bien, al considerar d_B y h_C, o d_C y h_B, se obtiene,
\displaystyle{A=\frac{\left|\left(y_3-y_1\right)x_2-\left(x_3-x_1\right)y_2+\left(x_3x_1\right)y_1-\left(y_3-y_1\right)x_1\right|}{2}},
\displaystyle{A=\frac{\left|\left(y_2-y_1\right)x_3-\left(x_2-x_1\right)y_3+\left(x_2x_1\right)y_1-\left(y_2-y_1\right)x_1\right|}{2}}.
32
Con esto se ha definido las propiedades de un triángulo
25. Problemas
Módulo III.
Lugares geométricos I: Circunferencia y elipse
En esta lección repasaremos uno de los conceptos más importantes en la geometría analítica, el de
“lugar geométrico”. También con especial atención estudiaremos dos lugares geométricos
notables: la circunferencia y la elipse. Así, los objetivos de la lección se pueden resumir en los
siguientes tres puntos:
1. Hacer conciente el significado de ``lugar geométrico'' y el proceso para representarlo
matemáticamente.
2. Revisar la representación matemática de las circunferencias utilizando la herramienta vectorial.
3. Revisar la representación matemática de las elipses utilizando la herramienta vectorial.
1.
Sobre los lugares geométricos
Una definición simple de lugar geométrico nos dice que es un conjunto de puntos que
obedecen alguna restricción geométrica. Los lugares geométricos, generalmente permiten
derivar relaciones matemáticas entre los puntos que los conforman y usualmente estas
ecuaciones son la forma más práctica de caracterizarlos. Entonces el problema matemático
asociado a este concepto es comúnmente encontrar las ecuaciones matemáticas que los
definen.
Supongamos ahora, como ejemplo, que se quiere encontrar la ecuación que representa al
lugar geométrico de los puntos que equidistan de dos puntos fijos A=(1,4) y B=(3,1). Para
hacerlo se puede usar una construcción como la que se muestra en la figura siguiente:
33
En la figura se trazaron los vectores u y v, asociándolos a los puntos A y B respectivamente. Un
vector w=(x,y) que apunte a cualquier punto contenido en el lugar geométrico debe cumplir
(como también puede verse en la figura) que sus distancias a los puntos A y B son iguales. Esta
condición se puede expresar usando operaciones vectoriales sobre los vectores z y s, los
cuales, como se observa, apuntan de D a A y de D a B respectivamente. La condición de
equidistancia se puede escribir entonces así:
\begin{displaymath} \vert z\vert=\vert s\vert, \end{displaymath}
(1)
o bien
\begin{displaymath} \sqrt{z \cdot z}=\sqrt{s \cdot s} \end{displaymath}
(2)
que equivale a igualar los argumentos de las raíces:
\begin{displaymath} z \cdot z= s \cdot s \end{displaymath}
(3)
Pero como podemos ver se cumple que z=u-w y s=v-w por lo que sustituyendo en 3,
\begin{displaymath} (u-w) \cdot (u-w) - (v-w) \cdot (v-w) =0. \end{displaymath}
(4)
Esta última ecuación es la relación vectorial que obedecen los puntos del lugar geométrico.
Para obtener una relación cartesiana entre sus coordenadas, sustituimos los valores de
u=(1,4), v=(3,1) y w=(x,y) quedando:
\begin{displaymath} (1-x)^2+(4-y)^2-(3-x)^2-(1-y)^2=0.\end{displaymath}
(5)
Desarrollando los binomios al cuadrado y simplificando nos lleva directamente a la ecuación:
\begin{displaymath} 4x-6y+7=0, \end{displaymath}
(6)
que es la ecuación de la recta que se muestra en color rojo. Noten que en la construcción es
posible mover el punto D arrastrándolo con el ratón y al mismo tiempo verificar que cualquier
punto en la recta cumple la condición pedida. También es interesante jugar con la
construcción variando A y B notando que se puede obtener la solución para cualquier par de
puntos. Esto quiere decir que todas las rectas están descritas por un lugar geométrico como
34
este. En otras palabras una recta también es ``el lugar geométrico de los puntos que
equidistan de dos puntos fijos''.
El ejemplo tiene dos enseñanzas: primero la manera como enunciar un lugar geométrico y
segundo la manera como encontrar la relación matemática que lo describe. Así el proceso
para encontrar la ecuación de un lugar geométrico puede resumirse como sigue:
1. Entender la definición propuesta.
2. Traducir a una construcción geométrica (basada en vectores o en cualquier otra técnica).
3. Obtener la relación matemática más simple que describe al lugar geométrico. Esto es
mediante una simplificación algebraica.
Elige ahora el siguiente paso, que puede ser ir a una serie de ejercicios de práctica o de
continuar con la sección de circunferencia.
2.
La circunferencia
Esta sección la empezaremos con un problema y discutiremos su solución:
El problema consiste en encontrar la ecuación del lugar geométrico de los puntos que están a
una distancia igual a 3 del punto A=(1,1).
Construcción: Usando vectores se puede hacer la siguiente construcción:
El vector u está asociado al punto A, el vector v es apunta al punto C, el cual pertenece al lugar
geométrico. El vector w va de A a C y por tanto cumple que w=v-u. La línea roja es el lugar
35
geométrico buscado, que claramente es una circunferencia. Prueba a mover con el ratón el
punto C, cualquier punto verifica la condición de estar a 3 unidades del punto A.
Solución matemática: Cualquier punto en el lugar geométrico esta a una distancia 3 de A, esto
en lenguaje de vectores se escribe así de simple:
|w|=3.
(7)
Pero por construcción w=v-u, entonces:
|v-u|=3,
(8)
que usando la relación entre el tamaño y el producto punto se puede escribir:
\sqrt{(v-u)\cdot(v-u)}=3.
(9)
Elevando al cuadrado la ecuación anterior también se puede escribir así:
\begin{displaymath} (v-u)\cdot(v-u)=9. \end{displaymath}
(10)
Esta última ecuación es la relación vectorial entre los puntos del lugar geométrico. La relación
cartesiana se puede hacer sustituyendo u=(1,1) y v=(x,y) de modo que:
\begin{displaymath} (x-1)^2+(y-1)^2=9. \end{displaymath}
(11)
Que es una relación más familiar.
Prueben a mover el punto A en le construcción. Es claro que la circunferencia sigue siendo la
misma pero el lugar geométrico es diferente. Sin embargo la ecuación (10) es la misma solo
hay que cambiar el valor al vector u. Si este fuera un valor cualquiera u=(x_0,y_0) la ecuación
cartesiana sería
(x-x_0)^2+(y-y_0)^2=9.
(12)
Finalmente la distancia de los puntos del lugar geométrico al punto A coincide con el radio de
la circunferencia, si lo definimos con R entonces las ecuaciones vectoriales y cartesianas de la
construcción geométrica quedarían así:
36
\begin{displaymath} (v-u)\cdot(v-u)=R^2, \end{displaymath}
(13)
y
\begin{displaymath} (x-x_0)^2+(y-y_0)^2=R^2. \end{displaymath}
(14)
En general, una circunferencia es entonces el lugar geométrico de los puntos que equidistan a
una distancia R de un punto fijo llamado centro.
3.
Elipses
Esta sección se puede iniciar enunciando la definición de elipse: ``una elipse es el lugar
geométrico de los puntos del plano tales que la suma de las distancias a dos puntos fijos
llamados focos es una constante''.
Gráficamente la construcción siguiente muestra los puntos que forman a una elipse, definida
por los puntos F1 y F2 (que son los focos) y la suma de distancia S (en este caso se escogió
S=9).
Observen en la construcción geométrica lo siguiente: el valor de S puede escogerse moviendo
el deslizador con el ratón, prueben cambiarlo y noten como cambia la elipse. También pueden
moverse los focos para cambiar la elipse. El punto B es parte del lugar geométrico y noten que
si se suman los tamaños de los vectores que lo unen con los focos u y v coincide con el valor
de S. Prueben mover B y noten que la suma siempre es S. Otra observación importante es que
37
hay un valor de S debajo del cual las elipses comienzan a dibujarse como rectas por que el
lugar geométrico realmente no existe. Esto sucede cuando S es menor que la distancia entre
los focos. En otras palabras, la suma de las distancias de cualquier punto en la elipse a los
focos debe ser siempre mayor a la distancia focal.
También es importante destacar que en la elipse se pueden ver dos ejes de simetría uno en la
dirección más larga y el otro perpendicular a éste. Cada uno de estos ejes divide a la figura en
partes iguales. De manera natural para distinguirlos se les llama eje mayor y eje menor. Los
puntos extremos de la elipse sobre los ejes se les llama vértices y el punto de intersección de
ellos es el centro de la figura. Finalmente un semieje de la elipse se define como un segmento
formado entre el centro y alguno de los vértices.
Los vectores u y v, de la figura son la base para deducir la ecuación que describe este lugar
geométrico pues su definición puede traducirse matemáticamente así:
\begin{displaymath} \vert u\vert+\vert v\vert=S. \end{displaymath}
(15)
Pero u y v son vectores relativos entre B y los focos F1 y F2. Para medirlos desde el origen
podemos usar los vectores auxiliares w, l y z, dibujados en líneas punteadas. En función de
estos u=l-w y v=l-z. Noten que l=(x,y) es cualquier punto en el lugar geométrico y en general
las coordenadas de los focos coinciden con w=(x_1,y_1) y z=(x_2,y_2). Entonces en general
una ecuación vectorial anterior se ve así:
\begin{displaymath} \vert l-w\vert+\vert l-z\vert=S, \end{displaymath}
(16)
o bien:
\begin{displaymath} \vert(x-x_1,y-y_1)\vert+\vert(x-x_2,y-y_2)\vert=S, \end{displaymath}
(17)
que equivale a la siguiente ecuación cartesiana:
\sqrt{(x-x_1)^2+(y-y_1)^2}+\sqrt{(x-x_2)^2+(y-y_2)^2}=S.
(18)
Esta ya es la ecuación cartesiana de la elipse pero en una versión poco elegante. Para
convertirla en una ecuación mas estandarizada hay que simplificar y el proceso algebraico para
hacerlo implica un buen rato de algebra. El proceso consiste tomar la ecuación elevarla al
cuadrado, desarrollar binomios al cuadrado, simplificar, volver a elevar al cuadrado y
simplificar de nuevo. El proceso es arduo y es un buen ejercicio algebraico. Sin embargo es
posible seguir un camino un poco mas heurístico partiendo de algunas simplificaciones.
38
Primero planteemos una elipse con centro en el origen como la que se muestra de rojo en la
siguiente figura:
Toda elipse tiene un eje mayor y un eje menor. En este caso el eje mayor esta en dirección al
eje x. Los valores a y b que se encuentran como deslizadores en la figura corresponden al valor
de los semiejes, en el caso inicial a el mayor y b el menor. Si se mueven los deslizadores la
elipse que se dibuja cambia e incluso a puede pasar a ser el mayor y b el menor. La
construcción importante es la circunferencia azul, la cual tiene un radio que coincide con el
semieje a. El vector r' describe un punto arbitrario sobre esta circunferencia, de hecho en la
figura puede moverse a voluntad arrastrándolo con el ratón, por esto lo describiremos como
r'=(x',y'). El vector r=(x,y) se construyó con las condiciones x'=x e y'=\frac{a}{b}y. Noten que así
definido el vector r' apunta siempre a un punto en la elipse. Ahora bien, como r' apunta a la
circunferencia sus coordenadas cumplen la ecuación de la circunferencia
\begin{displaymath} x'^2+y'^2=a^2, \end{displaymath}
(19)
su se sustituyen las condiciones mencionadas la ecuación anterior queda:
\begin{displaymath} x^2+(\frac{a}{b}y)^2=a^2, \end{displaymath}
(20)
que también al dividirse toda entre a^2 puede escribiese como:
\begin{displaymath} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1. \end{displaymath}
(21)
39
Que corresponde a la ecuación que describe al lugar geométrico de una elipse centrada en el
origen con semiejes de medida a y <b. Si el centro de la elipse estuviera fuera del origen,
digamos en C=(x_0,y_0) el razonamiento anterior puede aplicarse idéntico pero ahora la
circunferencia tendría una ecuación:
\begin{displaymath} (x'-x_0)^2+(y'-y_0)^2=a^2, \end{displaymath}
(22)
y se debe cumplir que x'=x e y-y_0=\frac{a}{b}(y-y_0) de modo que la ecuación de la elipse
será:
\begin{displaymath} \frac{(x-x_0)^2}{a^2}+\frac{(y-y_0)^2}{b^2}=1. \end{displaymath}
(23)
Ahora puedes continuar con los ejercicios de ejemplo de esta sección.
4. Problemas
5. Cuestionario
Módulo IV.
Lugares geométricos II: Parábolas e Hipérbolas
1. Parábola I
Se puede decir que cualquier conjunto de puntos, tal como la recta, la parábola, la elipse, etc.,
es un lugar geométrico \rho. El término lugar geométrico se aplica normalmente al conjunto
de todos los puntos que tienen alguna característica geométrica común.
En esta lección estudiamos a la parábola como el lugar geométrico de los puntos del plano que
equidistan de una recta y un punto fijo, donde el punto no pertenece a la recta. A esta recta se
le conoce como la Directriz d y al punto F como el Foco. La recta que contiene al foco de la
parábola y que es perpendicular a la directriz es el eje de la parábola. El punto V de la
intercesión de una parábola con su eje recibe el nombre de vértice.
2.
Parábola II
En la siguiente construcción al mover el punto P se dibuja la parábola. También se muestra
que la distancia entre el punto P y el foco, comparada con la distancia de un punto sobre la
directriz al foco es la misma. Además es fácil identificar que si el punto Q no pertenece al lugar
geométrico definido por la parábola, las distancias anteriores no coinciden.
40
Obtengamos la ecuación de la parábola que tiene su foco en el punto F(0,2) y cuya directriz d
es una recta con ecuación (ver figura de abajo)
y=-2,
obsérvese que U(x,y) sobre la parábola es un punto del lugar geométrico sí y solo sí
\left|u-f\right|=\left|u-w\right|,
donde W es la proyección (perpendicular) de U(x,y) sobre \rho. Entonces como U tiene las
coordenadas (x,y), F tiene como coordenadas a (0,2), y W tiene como coordenadas a (x,-2), se
tiene
\left|\left(x,y\right)-\left(0,2\right)\right| =\left|\left(x,y\right)-\left(x,-2\right)\right|,
\left|\left(x-0,y-2\right)\right|=\left|\left(x-x , y+2\right)\right|,
\sqrt{x^2+\left(y-2\right)^2} =\sqrt{0^2+\left(y+2\right)^2} ,
41
x^2+\left(y-2\right)^2} =\left(y+2\right)^2 ,
x^2+y^2 - 4 y +4 = y^2 +2 y +4 ,
x^2 =8 y .
Como las raíces cuadradas involucradas en este cálculo son no negativas, los pasos de este
proceso son reversibles y la gráfica de x^2 = 8 y es la parábola requerida.
3.
Parábola III
Mediante un razonamiento similar se puede demostrar que una ecuación de la parábola cuyo
foco es F(0,p) y cuya directriz es la recta d dada por y = -p es
x^2= 4 p y .
La ecuación anterior recibe el nombre de forma ordinaria de la ecuación de una parábola, con
vértice en el origen y foco sobre un eje de coordenadas. Si p>0, entonces la parábola se
abre hacia arriba. Si p<0, entonces la parábola se abre hacia abajo. Caso similar ocurre si
foco se encuentra en F(p,0) y cuya directriz es la recta d dada por x= -p . En este caso la
ecuación de la parábola es
y^2= 4 p x .
Si p>0, entonces la parábola se abre hacia la derecha. Si p<0, entonces la parábola se
abre hacia la izquierda.
Si se mueve la dirección de la directriz dejando fijo el foco entonces la parábola puede abrirse
hacia arriba o hacia abajo, hacia la derecha o izquierda tal como se observa en la siguiente
construcción.
42
Mueve en la figura superior, el punto “muéveme” que está sobre la recta, la directriz y
observa los cambios:
¿Puedes identificar las distintas formas de la parábola?
Visualiza también las parábolas cuando se deja fija la directriz pero se mueve el foco F.
¿Podrías escribir la ecuación las diferentes ecuaciones de las parábolas?
4.
Parábola IV
La forma general de la ecuación de la parábola con eje paralelo al eje y es
y = a x^2 + b x + c.
Esta parábola se abre hacia arriba si a>0 o bien hacia abajo si a<0. En la siguiente
construcción se puede observar la forma de la parábola moviendo los parámetros de la
ecuación general de la misma.
Mueve en la figura superior, los distintos parámetros a, b , y c de la ecuación de la recta y
observa los cambios:
¿Puedes identificar qué cambios provoca en la forma de la parábola cada uno de los
parámetros cuando dos de ellos se mantienen fijos?
5.
Aplicaciones I
Al girar una parábola alrededor de su eje, obtenemos una superficie de revolución llamada
paraboloide. Estas superficies tienen muchas aplicaciones, principalmente en óptica y
electrónica, ya que si un rayo de luz paralelo al eje choca contra el paraboloide, entonces se
refleja hacia su foco, e inversamente, si un rayo sale del foco y choca contra el paraboloide,
entonces se refleja en la dirección de su eje.
43
En la figura superior, mueve los puntos en rojo y en verde y observa los cambios:
¿Puedes identificar que independiente del punto en rojo p, los rayos que viajan paralelo al eje
del paraboloide siempre se reflejan hacia el foco F?
¿Puedes identificar que si lo rayos salen del foco F y van al paraboloide entonces se reflejan de
manera paralela a su eje?
Los rayos del sol por viajar miles de kilómetros antes de llegar a la tierra, se consideran
paralelos al incidir en un objeto por ejemplo una lente, y van al foco. Basado en esta idea,
¿podrías diseñar un concentrador solar? ¿Qué forma tendría?
Esta propiedad, conocida como la propiedad de reflexión o propiedad óptica de la parábola,
tiene muchas aplicaciones; por ejemplo, en los faros de los automóviles, las antenas
parabólicas, los telescopios, los micrófonos direccionales, etc.
6.
Hipérbola I
Como hemos visto en la sección anterior, la parábola es el lugar geométrico de los puntos del
plano tales que están a la misma distancia de una recta d, conocida como directriz, y de un
punto dado F, llamado foco de la parábola. En esta lección se estudiará el lugar geométrico
\rho determinado por la diferencia de dos distancias: la hipérbola.
7.
Hipérbola II
Sean F1 y F2 dos puntos en el plano, y sea k una constante tal que k < dist\left(F1,F2\right).
Donde dist\left(F1,F2\right) es la distancia entre los puntos F1 y F2. Sea U un punto en el
plano, y considérese la distancia entre U y F1 y la distancia entre U y F2. Supóngase que la
diferencia entre dichas distancias es igual a k. El conjunto de los puntos del plano
44
U\left(x,y\right) que cumplen esta propiedad forman una hipérbola. En la construcción de
abajo, se muestran los focos F1, F2, el eje principal, y el punto medio C que se refiere al centro
de la hipérbola. La hipérbola, a diferencia de las otras cónicas, está formada por dos partes
separadas llamadas ramas de la hipérbola.
Como puede observarse en la construcción de arriba, al mover el punto U2 se dibujan las dos
ramas de la hipérbola. Es claro que
\displaystyle{\left|dist\left(U1,F2\right)-dist\left(U1,F2\right)\right|
=\left|dist\left(U2,F1\right)-dist\left(U2,F2\right)\right| = Cte}.
Además es fácil identificar que si el punto Q no pertenece al lugar geométrico definido por la
hipérbola, la distancia \displaystyle{\left|dist\left(U2,F1\right)-dist\left(U2,F2\right)\right|} no
es una constante.
8.
Hipérbola III
Considérese ahora la hipérbola (ver figura de abajo) cuyo centro es el origen, cuyos focos son
F1(c,0) y F2(-c,0), y para la cual |dist(U,F1)-dist(U,F2)| = 2a, donde a es una constante positiva
tal que a<c, y U es un punto en la hipérbola. Entonces por definición, el punto U(x,y) está
sobre la hipérbola si y sólo si
|u-f1|-|u-f2|=2a,
o bien
|u-f1|-|u-f2|=\pm 2a.
45
Puesto que u=(x,y), f1=(c,0), y f2(-c,0), esta última ecuación se puede escribir en la forma
\sqrt{(x-c)^2+y^2}-\sqrt{[(x-(-c)]^2+y^2} =\pm 2a.
Si ahora se \sqrt{(x+c)^2+y^2} a ambos miembros de esta ecuación, y se eleva al cuadrado a
ambos términos resultantes se obtiene
(x-c)^2+y^2=4a^2\pm 4a\sqrt{(x+c)^2+y^2}.
Si ahora se eleva al cuadrado ambos miembros de la ecuación, simplificando y factorizando el
resultado se obtiene
x^2(c^2-a^2)+a^2(a^2-c^2)=a^2y^2.
Puesto que 0<a<c, se sigue que a^2<c^2 y c^2-a^2>0. Si se hace b^2=c^2-a^2,
entonces esta ecuación se reduce a
b^2x^2-a^2y^2=a^2b^2,
que finalmente dividiendo por a^2b^2, se llega
\displaystyle{\frac{x^2}{a^2}-\frac{y^2}{b^2}=1}.
En la siguiente construcción mueve los puntos a y b, parámetros de la ecuación general de la
hipérbola, y observa los cambios:
¿Puedes observar que los cambios en ramas de las hipérbolas?
46
9. Ejercicios
10. Cuestionario
Módulo V.
Coordenadas polares
En esta lección prestaremos una introducción a la representación de lugares geométricos en
coordenadas polares. Esta elección de coordenadas es especialmente útil sobre todo en el estudio
de las cónicas ya que, como se verá más adelante, permite englobar a todas ellas en una sola
expresión matemática general. Así los objetivos de esta sección son los siguientes:
1. Conocer la representación de los vectores en coordenadas polares y su relación con las
coordenadas cartesianas.
2. Explorar las ecuaciones que describen a las cónicas en coordenadas polares.
3. Conocer y razonar el concepto de excentricidad.
1.
Coordenadas polares
En la lección sobre los vectores se introdujo la figura siguiente y se hizo notar que un vector
además de tamaño tiene dirección y se encontró que para un vector u=(x,y) su tamaño y
ángulo de inclinación se calculan con las relaciones
\begin{displaymath} \vert u\vert=R=\sqrt{u \cdot u}=\sqrt{x^2+y^2} \end{displaymath}
(1)
y
\begin{displaymath} \alpha = \arctan \frac{y}{x}. \end{displaymath}
(2)
47
El valor de R está definido sin ambigüedad, es decir dado el punto su valor es único. Sin
embargo, el ángulo de inclinación si puede ser ambiguo porque un ángulo siempre se mide
relativo a una recta de referencia. En el caso de la figura, la recta es el eje x positivo y el ángulo
esta medido en grados. Esta elección es la que parece más natural, sin embargo presenta un
detalle técnico relacionado con los signos, pues un punto en los cuadrantes donde las
coordenadas son mixtas (positivas y negativas) la función "\arctan" (arco tangente o tangente
inversa) regresa valores de ángulos negativos. Para recuperar el ángulo entre 0^\circ y
360^\circ, que equivale a entre 0 y 2\pi radianes se debe aplicar la corrección siguiente (para
más detalle checar esta página):
\begin{displaymath}\alpha=\left \lbrace \begin{array}{lll}\arctan (\frac{y}{x}) &
\mathrm{si} & x>0,\ y\geq 0 \\ \arctan (\frac{y}{x}) +2\pi & \mathrm{si} &
x>0,\ y < 0 \\ \arctan (\frac{y}{x}) +\pi & \mathrm{si} & x<0 \\ \frac{\pi}{2}
& \mathrm{si} & x=0 ,\ y >0\\ \frac{3\pi}{2} & \mathrm{si} & x=0,\ y
< 0 \end{array}\rigth.\end{displaymath},
donde asumimos que el resultado se desea radianes lo cual suele ser más cómodo para hacer
cálculos, pero si se desea en grados simplemente se usa así:
\begin{displaymath}\alpha=\left \lbrace \begin{array}{lll}\arctan (\frac{y}{x}) &
\mathrm{si} & x>0,\ y\geq 0 \\ \arctan (\frac{y}{x}) +360^\circ & \mathrm{si}
& x>0,\ y < 0 \\ \arctan (\frac{y}{x}) +180^\circ & \mathrm{si} & x<0 \\
90^\circ & \mathrm{si} & x=0 ,\ y >0\\ 270^\circ & \mathrm{si} & x=0,\
y < 0 \end{array}\rigth.\end{displaymath}.
En el ejemplo de la figura el vector u=(6,4) tiene un tamaño \vert u\vert=7.21 y
\alpha=33.69^\circ, estos dos valores corresponden a lo que entendemos por sus
``coordenadas polares''. Se puede mover el punto B con el ratón para crear diferentes vectores
y observar los ángulos y los tamaños que definen sus coordenadas polares.
48
Si se tiene un vector definido en coordenadas polares, cabe la pregunta ¿cómo obtengo sus
coordenadas cartesianas x, y? En el ejemplo mencionado podemos ver que el punto B forma
un rectángulo dividido en dos por el vector u. Los triángulos que resultan de esta división son
iguales, pero reflejados respecto al vector, sin importar donde este colocado B (prueben
moverlo e intenten observar esta propiedad). Cualquier triángulo entonces tiene como catetos
a las coordenadas x e y y como hipotenusa a \vert u\vert=R, entonces se relacionan con el
ángulo \alpha mediante alguna función trigonométrica. En especial el seno y el coseno, de
modo que identificando a x como el cateto adyacente a \alpha y a y como el opuesto, sucede
que
\begin{displaymath} x=R \cos \alpha \end{displaymath}
(3)
y
\begin{displaymath} y=R \sin \alpha. \end{displaymath}
(4)
Usar coordenadas polares puede representar ventajas para algunos casos particulares, sin
embargo siempre hay un costo que pagar, por ejemplo, la suma en estas coordenadas no es la
suma de los tamaños y la suma de los ángulos. Hacer una suma implica regresar a las
componentes cartesianas y aplicar la definición de suma por componentes para al final volver
a coordenadas polares. Esto se hace comúnmente en física, por ejemplo cuando se suman
vectores de fuerza donde se conoce la magnitud de la fuerza y el ángulo al cual se aplica.
Sin embargo así como la suma se complica, el producto por escalar y el producto punto entre
vectores se simplifican, en estas coordenadas si un vector se escribe u_{\alpha}=(R,\alpha)
entonces al multiplicarlo por un escalar t no hay cambio en su dirección, solo en su tamaño,
por tanto
\begin{displaymath} t u_\alpha=(t R,\alpha). \end{displaymath}
(5)
De aquí se puede deducir que un vector cuya componente radial sea negativa, se genera
multiplicando otro vector por t=-1, es decir un signo simplemente indica un cambio en la
dirección del vector. Este cambio también podría interpretarse como un giro de 180^\circ en
el vector, el cual no cambia la dirección. De modo que (-R, \alpha)=(R,\alpha+180^\circ) si
0<\alpha<180^\circ
y
(-R,
\alpha)=(R,\alpha-180^\circ)
si
180^\circ<\alpha<360^\circ.
Si tenemos dos vectores en coordenadas polares u_\alpha=(R,\alpha) y v_{\alpha'}=(R',\alpha')
entonces usando la relación (ver lección de vectores)
49
\begin{displaymath} u_\alpha \cdot v_{\alpha'} = \vert u_\alpha \vert\vert v_{\alpha'}
\vert\cos \theta, \end{displaymath}
(6)
donde \theta es el ángulo entre ambos vectores, es decir \theta=\alpha-\alpha', con lo que se
tiene que
\begin{displaymath} u_\alpha \cdot v_{\alpha'} = R R' cos(\alpha-\alpha'). \end{displaymath}
(7)
Noten que en las últimas ecuaciones utilizamos la notación u_\alpha, interpretándola como el
vector u escrito en coordenadas polares.
Estos son las nociones básicas para trabajar con ecuaciones en coordenadas polares. Ahora
podemos pasar a repasar algunos ejemplos.
2.
Ecuaciones en coordenadas polares
Un vector en coordenadas polares u_\alpha=(R,\alpha) describe un punto en el plano. Si el
valor de R se hace variar en función del ángulo \alpha, se obtiene un conjunto de vectores que
dibujan ahora un lugar geométrico. Para comprender este concepto mejor tomemos un
ejemplo, imaginemos que R=1+\alpha (midiendo \alpha en radianes). Al variar \alpha entre 0 y
2\pi el vector u_\alpha va dibujando la figura que se muestra en la construcción siguiente
(para construirla presiona el botón de inicio de animación, para que varíe los valores de
\alpha):
50
la figura se trata de una porción de una espiral. Cambia los parámetros k y a en la figura y nota
como la espiral cambia sus proporciones. Es importante mencionar cómo se hizo la
construcción en geogebra. En ésta versión del programa no hay (todavía) una herramienta
para graficar ecuaciones polares, sin embargo, siempre es posible dibujar un vector en
coordenadas cartesianas. El vector u en coordenadas cartesianas que corresponde al vector
u_\alpha=(R(\alpha),\alpha) es simplemente:
u=(R(\alpha) \cos \alpha,R(\alpha) \sin \alpha),
que para el caso de la espiral queda descrito así:
u=( (a+ k \alpha)\cos \alpha,(a+ k \alpha) \sin \alpha),
este vector si se puede dibujar directamente utilizando un "deslizador" que varíe \alpha. En el
ejemplo se usaron también deslizadores para cambiar variar los parámetros a y k.
Cabe mencionar aquí que siempre que tengamos una ecuación para R(\alpha) es posible
obtener un lugar geométrico. De hecho la elección puede dar resultados espectaculares.
Tomemos ahora por ejemplo
R(\alpha)=a \cos (k \alpha).
Noten que R puede tomar valores positivos o negativos, lo cual suena absurdo siendo que R
representa el tamaño del vector, sin embargo si hacemos consciente que el cambio de signo
solo representa un cambio de dirección y nos permitimos esa libertad, el dibujo que resulta
tomando a=2 y k=4 queda así (presiona nuevamente el botón para iniciar la animación o
mueve el deslizador de \alpha):
51
la figura se llama Rosa Polar, y es diferente para valores distintos de a y k, prueba a
cambiarlos. El vector en coordenadas cartesianas que permite dibujar esta figura se escribe
así:
u=(a \cos (k \alpha) \cos \alpha,a \cos (k \alpha) \sin \alpha).
La pregunta en este punto es como se describen las cónicas con este tipo de ecuaciones, lo
cual se discutirá en la siguiente sección.
Ecuaciones polares de las cónicas.
Empecemos planteando un problema en forma de lugar geométrico: Encontrar la ecuación en
coordenadas polares de la elipse que tiene los focos en F1=(0,0) y F2=(4,0) y tiene un vértice
en V=(-2,0).
La solución es como sigue: El problema lo que implica es encontrar la función R(\alpha) que
describa a la elipse dada. Esta elipse se ve como lo muestra la figura siguiente. Ahí, el vector u
describe un punto arbitrario sobre la recta (recuerda que arbitrario quiere decir que lo puedes
mover con el ratón), pero como un foco está en (0,0) es también el vector que une el foco F1
con el punto. El vector w se escogió como el vector que va de F2 al mismo punto arbitrario y el
vector p apunta del origen (o F1) F2, es horizontal y su tamaño es la distancia focal f, en este
caso \vert p\vert=f=4.
La ecuación vectorial de la elipse nos dice que:
\begin{displaymath} \vert u\vert+\vert w\vert=S, \end{displaymath}
(8)
52
donde S es la suma de las distancias de cualquier punto a los focos, en particular del vértice V.
De la figura, la distancia de V a F1 es 2 y de V a F2 vale 6, por tanto S=2+6=8, que como vimos
es el tamaño del eje mayor A. Por otro lado, también podemos observar que el vector u tiene
coordenadas polares u=(R,\alpha) por lo que \vert u\vert=R y además se cumple que w=u-p,
por tanto la ecuación [*] queda así:
\begin{displaymath} R+\vert u-p\vert=2a, \end{displaymath}
(9)
o bien así:
\begin{displaymath} \vert u-p\vert=A-R, \end{displaymath}
(10)
que implica que:
\begin{displaymath} \vert u-p\vert^2=(A-R)^2. \end{displaymath}
(11)
Pero como
\begin{displaymath} \vert u-p\vert^2=(u-p) \cdot (u-p)= \vert u\vert^2+\vert p \vert ^2-2\vert
u\vert\vert p\vert\cos \alpha=R^2+f^2-2R f\cos \alpha, \end{displaymath}
(12)
la ecuación equivale a
\begin{displaymath} R^2+f^2-2 R f\cos \alpha=(A-R)^2. \end{displaymath}
(13)
Finalmente, desarrollando el binomio del lado derecho simplificando y despejando R queda:
\begin{displaymath} R=\frac{(A^2+f^2)/A}{1-\frac{f}{A}\cos \alpha }. \end{displaymath}
(14)
Que sustituyendo los valores mencionados A=8 y f=4 queda:
\begin{displaymath} R=\frac{3}{1-\frac{1}{2}\cos \alpha }. \end{displaymath}
(15)
En general, toda elipse con eje mayor horizontal y un foco en el origen estará representada
por una ecuación como esta de modo que:
53
\begin{displaymath} R=\frac{l}{1-e \cos \alpha}, \end{displaymath}
(16)
donde ahora l y e son dos constantes que dependen de su forma. El valor de l se puede
interpretar fácilmente, haciendo \alpha=90^\circ en la ecuación anterior. Esto corresponde a
tener un punto justo sobre el origen (prueben a hacerlo en la construcción de ejemplo). El
radio que define a este punto vale R=l que podemos recordar corresponde a la mitad del lado
recto de la elipse. Si L es el tamaño del lado recto l=L/2. Por otro lado e=\frac{f}{A} y es tan
importante que se le llama excentricidad y por tanto lo discutiremos en una sección especial.
Para tener más información sobre las ecuaciones polares de las cónicas restantes continúa con
los ejercicios de ejemplo de esta sección.
3.
Sobre la excentricidad
De los problemas planteados y resueltos en la sección anterior se pueden inferir las siguientes
conclusiones:
1. Todas las ecuaciones polares de las cónicas cumplen una relación como esta:
\begin{displaymath} R=\frac{l}{1 \pm e \cos \alpha}. \end{displaymath}
(39)
Dónde l es la mitad del lado recto de la figura, e se define como excentricidad, que
corresponde con el cociente de la distancia focal entre la distancia entre vértices y el signo
\pm indica el origen esta en el foco izquierdo o derecho respectivamente.
2. Si en esta relación se toma e=0 se obtiene una circunferencia.
3. Si en esta relación se toma e=1 se obtiene una parábola.
4. Si los valores de e son mayores que 1 se dibujan hipérbolas.
5. Si los valores de e son menores que 1 se dibujan elipses.
Lo verdaderamente importante es que existe una ecuación general para las cónicas en
coordenadas polares muy simple y que depende del lado recto y la excentricidad, esta última
es igual al cociente entre la distancia focal F y la distancia entre los vértices A, de modo que:
\begin{displaymath} e=\frac{F}{A}. \end{displaymath}
(40)
Así en la circunferencia F=0 porque hay solo un foco. En la parábola solo hay un foco pero se
comporta como una elipse donde el segundo foco se separo una distancia muy grande, de
54
hecho infinita. En esa circunstancia el cociente de F y A debe ser 1. Finalmente, en una
hipérbola siempre la distancia focal es mayor a la distancia entre sus vértices y en la elipse
esta relación se invierte.
Revisemos ahora el siguiente problema y su solución: encontrar la ecuación polar del lugar
geométrico de los puntos cuya distancia al origen es proporcional a la distancia a la recta x=p.
Solución: El lugar geométrico buscado suena como la definición de una parábola salvo por la
palabra ``proporcional''. Si tomamos u como el vector que apunta a un punto arbitrario del
lugar geométrico buscado, la ecuación vectorial que debe describir este lugar geométrico se
traduce así:
\begin{displaymath} \vert u\vert=k(p-\vert u\vert\cos \alpha), \end{displaymath}
(41)
donde k es una constante de proporcionalidad y \alpha es el ángulo respecto al eje x. Si \vert
u\vert=R podemos sustituir y despejar de modo que:
\begin{displaymath} R=\frac{pk}{1+k \cos \alpha}. \end{displaymath}
(42)
Dependiendo de los valores de p y k esta ecuación describe alguna cónica, por lo que el lado
recto es l=pk y el valor absoluto de k coincide con la excentricidad, es decir \vert k\vert=e.
Prueba la siguiente animación, ahí se puede controlar con un deslizador el valor de k y con el
otro el ángulo \alpha. Selecciona el valor de k y prueba iniciar la simulación. También se puede
mover el punto P por el que pasa la directriz. Con los criterios de la excentricidad dados
anteriormente se pueden obtener todas las cónicas. Solo se queda una pregunta de reflexión
que dejaremos abierta ¿Cómo se puede dibujar un circulo en la construcción?
Resumiendo, la excentricidad de un lugar geométrico definido por un foco fijo y una directriz
se define como el conciente entre la distancia de cualquier punto al foco y la distancia del
mismo punto a la directriz. Es deciír:
55
\begin{displaymath} e=\frac{distancia[u,F]}{distancia[u,D]}, \end{displaymath}
(43)
con u representando al punto F al foco y D a la recta directriz. Curiosamente en las cónicas
este cociente coincide con el cociente de la distancia focal entre la distancia entre vértices, tal
y como se destacó en la sección anterior.
Como conclusión podemos decir que todas las cónicas pueden generalizarse en una sola
descripción como lugar geométrico y en una ecuación general, donde solo es necesario
conocer dos parámetros: el lado recto y la excentricidad, de ahí su importancia.
4. Ejercicios de Aplicación
5. Cuestionario
Módulo VI.
Tangentes a cónicas
En esta sección abordaremos un problema que en su momento constituyó un reto fundamental de
geometría analítica y que también fue una motivación que llevó al desarrollo del cálculo
diferencial: el problema de las tangentes a curvas planas. Los objetivos, para este caso, se pueden
resumir en los siguientes puntos:
1. Recordar los métodos analíticos para resolver el problema de tangentes a cónicas.
2. Valorar lo que llamaremos el Método Diferencial para obtener tangentes a curvas.
Por tanto esta lección se dividirá en dos secciones principales, cada una con un conjunto de
ejercicios. Recomendamos empezar por la sección “Secantes y tangentes” al menos la primera vez
que se realice la sección.
1.
Secantes y tangentes
En general cuando se tiene un conjunto de puntos que describen un lugar geométrico, éste
puede interceptarse en uno o varios puntos con una recta dada. En particular si se trata de
cónicas, una recta solo puede hacer intersección con ellas en uno, dos o ningún punto. De
entrada se podría demostrar que es imposible que se cruce en más de dos. Cuando una recta
tiene dos intersecciones la bautizamos (o definimos) con el nombre de “secante” a la curva. Si
hay solo una intersección se trata de una “tangente”. En la siguiente figura, se pueden
observar las secantes y las tangentes a una cónica. Presionando el botón para iniciar
animación se puede observar como una recta de pendiente m y ordenada al origen b puede o
no hacer intersección a la cónica. La animación cambia de manera continua el valor de b pero
con los deslizadores pueden cambiarse también la pendiente de la recta y los parámetros de la
cónica. Variando la excentricidad representada con el valor e se pude obtener cualquier cónica
con lado recto igual al doble del valor del deslizador l. Los puntos de intersección están
definidos por D y C y se nota como pueden estar o no definidos.
56
La solución gráfica que se muestra en geogebra tiene una contraparte algebraica que puede
seguirse de la siguiente manera:
* Tomemos la ecuación de una cónica centrada en un foco, con excentricidad e y semilado
recto l. En coordenadas polares es:
R=\frac{l}{1-e \cos \alpha}.
* Usando que R=\sqrt{x^2+y^2} y x=R \cos \alpha, en la ecuación anterior obtenemos la
ecuación cartesiana:
(1-e^2)x^2-2lex+y^2=l^2.
Que si ponemos a=(1-e^2), b=-2le y c=1 y d=-l^2 tiene la forma general
a x^2 +b x+c y^2 +d=0.
* Para que la recta y=mx+b intersecte a esta cónica es necesario que las dos ecuaciones
tengan soluciones simultáneamente. Para hacerlo se puede sustituir y=mx+b en la cónica y
resolver la ecuación de segundo grado para x:
(b^2 + d )+ (b + 2 b m) x + (a + m^2) x^2=0
* La ecuación de segundo grado se puede resolver de manera general para x quedando:
x_\pm=\frac{-(b+2 b m)\pm\sqrt{(b+2 b m)^2-4 \left(a+m^2\right) \left(b^2+d\right)}}{2
\left(a+m^2\right)}.
* Las coordenadas y de los puntos de intersección son y_\pm=m x_\pm +b.
Noten que si el discriminante es menor que cero la raíz en la solución no se puede calcular lo
que indica que no hay intersección y si el discriminante se hace cero tenemos una tangente.
De este modo una recta tangente a esta cónica centrada en un foco debe cumplir que
57
(b+2 b m)^2-4 \left(a+m^2\right)\left(b^2+d\right)=0.
Este ejemplo permite ayudar a plantear y resolver el problema importante de esta sección,
que de alguna manera es al revés del anterior, pues dado un punto sobre una cónica se trata
de encontrar la ecuación de la recta que pasa por él y es tangente a la curva. Así, para resolver
el problema hay que suponer que e y l están dadas y se tiene que determinar m y b en un
punto seleccionado (x_0,y_0). Ilustremos la solución con un ejemplo.
Supongamos que e=\frac{1}{2} y l=2, es decir la cónica es una elipse con ecuación:
\frac{3}{4}x^2-2x+y^2=4,
y se desea encontrar la tangente en el punto A=(0,2). Lo primero es verificar que el punto esta
en la cónica, lo cual se hace sustituyendo en la ecuación y verificando la igualdad, lo cual es
cierto. Como el punto está en la recta tangente y=mx+b se cumple que
2= m(0)+b.
Por lo que b=2. Entonces todos los puntos de la recta cumplen que y=mx+2. Para encontrar la
intersección de esta recta con la cónica sustituimos y en su ecuación por lo que:
\frac{3}{4}x^2-2x+(m x+2)^2=4,
de modo que, desarrollando y simplificando queda la ecuación:
(m^2 +\frac{3 }{4})x^2+(4 m -2)x =0.
Como en el ejemplo anterior esta ecuación tiene una sola solución solo si su discriminante vale
cero, es decir si:
(4m-2)^2-4(m^2 +\frac{3 }{4})(0)=0
o bien:
(4m-2)^2=0.
lo que se cumple solo si m=\frac{1}{2} de modo que la tangente debe tener por ecuación
y=\frac{1}{2}x+2,
Este procedimiento es general para resolver el problema y se puede resumir de la siguiente
manera:
1. Con el punto donde pasa la tangente se determina la ordenada al origen de la recta
tangente en función de su pendiente.
2. Se sustituye la ecuación de la recta parcialmente conocida en la ecuación de la cónica.
3. Se plantea la ecuación de segundo grado que resuelve las intersecciones.
58
4. Se calcula el discriminante de esa ecuación y se iguala a cero; de ahí se despeja la pendiente
de la recta tangente.
2.
Método diferencial
Empezamos ahora con un ejemplo. Tenemos una elipse cuya ecuación cartesiana es:
x^2+3y^2=1.
Esta se muestra en la construcción siguiente:
A la construcción se agregaron los puntos C y D sobre la elipse, las coordenadas en el eje x de
estos dos están representadas por los puntos A y B y su diferencia es h. Las coordenadas en el
eje y, de estos mismos, los representan los puntos F y E y su diferencia vale k. Se agregó un
deslizador con una variable h que controla la posición de B, es decir la coordenada x del punto
D. Al mover el deslizador se puede notar como decreciendo h el punto D se aproxima a C. Se
trazaron también la recta secante que pasa por C y D (nombrada d) y la tangente a la elipse en
C (nombrada g). Noten que al decrecer h al mínimo la recta d se aproxima a g tanto como se
quiera. Es decir cuando h tiende a cero (sin ser cero) la pendientes de ambas rectas se
aproximan mucho hasta el punto de ser iguales. Esto induce a pensar un método para
determinar la pendiente de la recta tangente a partir de la recta secante.
Si generalizamos el punto C a C=(x_0,y_0) entonces el punto D estaría dado por
D=(x_0+h,y_0+k). De la figura se puede ver que la pendiente de la recta secante es:
m_s=\frac{k}{h} por lo que D=(x_0+h,y_0+m_s h).
Como C está en la elipse, entonces cumple su ecuación:
x_0^2+3y_0^2=1. (1)
Como D también está en la elipse, entonces también cumple su ecuación:
(x_0+h)^2+3(y_0+m_s h)^2=1. (2)
59
Si ahora desarrollo los cuadrados perfectos:
x_0^2 +2 h x_0 +h^2+3(y_0^2+2 m_s h y_0+m_s^2 h^2)=1,
por lo que distribuyendo el 3 y arreglando los términos
(x_0^2+3y_0^2)+ 2 h x_0+6 m_s h y_0+h^2+m_s^2 h^2=1.
Pero noten que lo que dejamos entre paréntesis es la ecuación para el punto C por lo que se
puede sustituir por un 1, que a su vez se elimina con el miembro derecho de la ecuación, por
tanto:
2 h x_0+6 m_s h y_0+h^2+m_s^2 h^2=0.
Finalmente factorizando una h y eliminándola, queda que:
2 x_0+6 m_s y_0+h+m_s^2 h=0.
Si ahora tomamos h=0, lo que equivale a juntar los dos puntos queda simplemente que:
2 x_0+6 m_s y_0=0, (3)
de donde se puede despejar m_s, de modo que:
m_s=-\frac{x_0}{3 y_0}.
Pero al haber hecho h=0 la secante coincide con la tangente por lo que m_s es también la
pendiente de la tangente m_t. En especial en el dibujo C=(\frac{1}{2},\frac{1}{2}) de modo que
m_t=-\frac{1}{3}, lo cual puede verificarse gráficamente.
Aquí hay que resaltar dos puntos, al desarrollar la ecuación (2), encontramos información
escondida en ella, si ahí se toma h=0 no permite obtener el valor de m_s. Es el desarrollo
algebraico el que libera la información. Así para resolver el problema exactamente es
necesario desarrollar las ecuaciones y luego tomar el valor de h=0. Este proceso coincide con
lo que se conoce por el concepto de límite y en particular el proceso resultante se llama
derivación.
Para aquellos que saben derivar noten que la ecuación de la elipse era:
x^2+3y^2=1
si derivo respecto a x cada término:
2 x +6 y \frac{dy}{dx}=0,
y despejo \frac{dy}{dx}:
\frac{dy}{dx}=-\frac{x}{3y}.
60
Por tanto la pendiente de la tangente al punto (x_0,y_0) es m_t=\frac{dy}{dx}=\frac{x_0}{3y_0}, es decir es la derivada de la variable y en función de x evaluada en el punto
dado.
Si sabemos derivar encontrar las pendientes de las tangentes es directo. De hecho el cálculo
diferencial se construyó para formalizar este método de obtención de tangentes, el cual se
cómo se puede notar resuelve un problema algebraico laborioso en tres pasos.
En esta liga están las tablas con las derivadas de las funciones básicas. Para un maestro de
geometría analítica dominar el cálculo diferencial es un arma inapreciable en la solución de
problemas con un nivel de complejidad mayor. Este curso no pretende extenderse mas, sin
embargo espero que sea un estimulo para recordar y ampliar por cuenta propia los conceptos
del cálculo diferencial.
3.
4.

Ejercicios
Cuestionario
4.1. Contenido Adicional. Ejercicios de Entrenamiento
Examen Final
61
Banco de preguntas
Vectores
1. Tenemos los vectores u=(3,5), w=(-2,1) y s=(0,6). Encuentra un vector v para cual la
ecuación w+s=v-u se cumple.
a. $$v\=(1,12)$$
b. $$v\=(-5,2)$$
c. $$v\=(0,7)$$
2. Determine si los vectores (-3,7), (6,-14) son paralelos perpendiculares o bien oblicuos.
a. Paralelos
b. Perpendiculares
c. Oblicuos
3. ¿Cuál es el par ordenado (x,y) tal que la flecha que va de A=(-1,-2) a B=(x,y) representa el
mismo vector que el vector que va de C=(2,4) a D=(8,-2)?
a. $$B\=(5,-8)$$
b. $$B\=(-5,8)$$
c. $$B\=(7,-4)$$
4. ¿Cuál es el valor de y que hace al vector v=(-4,y) ser perpendicular a w=(3,2)?
a. $$y\=6$$
b. $$y\=3$$
c. $$y\=0$$
5. Calcule el ángulo que se forma entre los vectores v=(-4,3) y w=(1,0). Elige la opción
correcta.
a. el ángulo es 2.49 radianes
b. el ángulo es 110 grados
c. el ángulo es 0 grados
6. Elige de las opciones que se presentan aquella que tenga un vector unitario (es decir de
tamaño 1) que apunte en la misma dirección del vector u=(1,3).
a. $$(\frac\{1\}\{\sqrt\{10\}\},\frac\{3\}\{\sqrt\{10\}\})$$
b. $$(\frac\{1\}\{\sqrt\{4\}\},\frac\{3\}\{\sqrt\{4\}\})$$
c. $$(\frac\{1\}\{\sqrt\{2\}\},\frac\{1\}\{\sqrt\{2\}\})$$
7. Si definimos los vectores u=(3,1), v=(-1,-3), w=(-2,1), s=(1,-1) y r=(w+s) \cdot s ( w\frac{1}{2}v ); calcula y captura en el espacio de "respuesta" el valor del tamaño de r.
a. 2.92
8. ¿Cuánto vale la proyección del vector v=(-2,3) sobre el vector u=(3,1)?
a. -0.94
9. Tenemos dos vectores u=(2,1) y v=(-1,2) que representan dos lados del triángulo con
vértices en (0,0), (2,1) y (-1,2). Si w es un vector que representa al tercero de sus lados,
calcula el valor absoluto de la proyección de w sobre v y da entrada a la respuesta.
62
a. 2.24
10. Dados los vectores u=(2, k) y v= (3, - 2), calcula el valor de k para que u y v sean
perpendiculares.
a. 3
11. Si tenemos dos vectores u=(1,0) y v=(0,9) ¿cuánto vale la proyección de u sobre v?
a. 0
12. ¿Cuál es el par ordenado (x,y) tal que el vector que va de A=(x,y) a B=(6,-2) representa el
mismo vector que la flecha que va de C=(4,-7) a D=(3,1)?
a. $$A\=(7,-10)$$
b. $$A\=(5,6)$$
c. $$A\=(1,-4)$$
Lugares Geométricos I
1. Selecciona la ecuación del lugar geométrico de los puntos P=(x,y) tales que la pendiente
del segmento que conecta a cada punto P con S=(1,-3) es el doble de la pendiente del
segmento que lo conecta con T=(3,2)
a. $$y\=\frac\{7x-13\}\{x+1\}$$
b. $$y\=\frac\{1\}\{2\}(5x-11)$$
c. $$y\=\frac\{1\}\{2\}(5x+11)$$
d. $$y\=-\frac\{8x-20\}\{x-5\}$$
2. Selecciona la ecuación del lugar geométrico de los puntos P=(x,y) tales que la pendiente
del segmento de recta que conecta cada punto P conS=(1,-2) es 3 unidades menor que la
pendiente del segmento de recta que conecta al punto con T=(-1,2).
a. $$y\=\frac\{1\}\{2\}(3-4x-3x^2)$$
b. $$y\=\frac\{1\}\{2\}(-3-4x-3x^2)$$
c. $$y\=\frac\{4x-2\}\{x-2\}$$
3. Se tiene un lugar geométrico descrito por los puntos P tales que la pendiente del
segmento que va de P a un punto A es cuatro veces la pendiente de P a un punto B. Si u, v
y w son tres vectores que van del origen a los puntos P, A y B respectivamente y se utilizan
los vectores unitarios i=(1,0) y j=(0,1), deduce y selecciona la ecuación vectorial que
describe al lugar geométrico.
a. $$\frac\{(u-v) \cdot j\}\{(u-v)\cdot i\}\=4 \frac\{(u-w) \cdot j\}\{(u-w)\cdot
i\}$$
b. $$ 4 \frac\{(u-v) \cdot j\}\{(u-v)\cdot i\}\= \frac\{(u-w) \cdot j\}\{(u-w)\cdot i\}$$
c. $$\frac\{(u-v) \cdot i\}\{(u-v)\cdot j\}\=4 \frac\{(u-w) \cdot i\}\{(u-w)\cdot j\}$$
4. Se tienen dos circunferencias iguales de radio r=3. El centro de la primera se encuentra en
el punto C_1=(3,-2) y el de la segunda en C_2=(3,2). Selecciona de la opciones, el par de
puntos donde se intersectan ambas circunferencias.
a. $$(3-\sqrt\{5\},0)$$ y $$(3+\sqrt\{5\},0)$$
b. $$(-\sqrt\{5\},0)$$ y $$(\sqrt\{5\},0)$$
c. No se intersectan en ningún punto.
63
5.
6.
7.
8.
9.
10.
d. $$(2-\sqrt\{5\},0)$$ y $$(2+\sqrt\{5\},0)$$
Una circunferencia está representada por la ecuación x^{2}+y^{2}-2x-4y-20=0. ¿Dónde
está colocado su centro y cuánto vale su radio?
a. Centro en $$(1,2)$$ y radio $$r\=5$$.
b. Centro en $$(-1,-2)$$ y radio $$r\=25$$.
c. Centro en $$(2,1)$$ y radio $$r\=5$$.
d. Centro en $$(2,-1)$$ y radio $$r\=25$$.
Un objeto gira alrededor del origen de un plano cartesiano de modo que a un tiempo t se
encuentra en la posición dada por el vector u=(3 \cos 2t, 3 \sin 2t). Elige entre las opciones
a la ecuación cartesiana de la figura que dibuja la trayectoria de este objeto.
a. $$x^2+y^2\=9$$
b. $$(x-2)^2+(y-2)^2\=9$$
c. $$x^2+y^2\=3$$
d. $$\frac\{x^2\}\{9\}+\frac\{y^2\}\{4\}\=1$$
Una elipse tiene una ecuación cartesiana 9x^2+4y^2-36=0. Cuál será la ecuación de una
circunferencia que tiene el mismo centro que esta elipse y se encuentra inscrito en ella.
a. $$x^2+y^2\=4$$
b. $$x^2+y^2\=2$$
c. $$x^2+y^2\=9$$
d. $$x^2+y^2\=36$$
¿Cuál es la ecuación de la elipse que tiene sus focos en F_1=(-3.0) y F_2=(3,0) y tiene un
vértice en V_1=(0,2)?
a. $$\frac\{x^2\}\{13\}+\frac\{y^2\}\{4\}\=1$$
b. $$\frac\{x^2\}\{13\}+\frac\{x^2\}\{4\}\=1$$
c. $$\frac\{x^2\}\{2\}+\frac\{x^2\}\{\sqrt\{13\}\}\=1$$
d. $$ x^2+x^2\=26$$
¿Cuánto vale el lado recto de la elipse descrita por la ecuación cartesiana \frac{(x1)^2}{4}+\frac{(y-1)^2}{9}=1?
a. 2.66
Una circunferencia pasa por tres puntos A=(1,0), B=(6,0) y C=(3,3). Usando geogebra,
encuentra el radio de la circunferencia que pasa por ellos y captura su valor en el espacio
de respuesta. Redondea a dos decimales tu resultado.
a. 2.55
Lugares Geométricos II
1. ¿Cuál es la ecuación de la parábola con vértice en el origen y foco F(0,5), y cuál es la
ecuación de su directriz?
a. Parábola $$y^2\=20x$$; directriz $$y\=-25$$
b. Parábola $$x^2\=20y$$; directriz $$y\=-25$$
c. Parábola $$x^2\=20y$$; directriz $$y\=-5$$
d. Parábola $$y^2\=20y$$; directriz $$x\=-5$$
64
2. Encuentra la ecuación del círculo que pasa por los focos de las hipérbolas cuyas
ecuaciones son 9x^2-16 y^2=144 y 16y^2-9x^2=144. Dibuja las hipérbolas y el círculo.
Utiliza Geogebra para dibujar la ecuación y sube tu archivo aquí.
a. $$x^2 +y^2\=16$$
b. $$x^2 +y^2\=25$$
c. $$x^2+y^2\=9$$
d. $$x^2+y^2\=\sqrt\{52\}$$
3. Calcule las coordenadas del foco, obtenga una ecuación cartesiana de la directriz y de la
parábola con vértice en el origen y que pasa por los puntos S(3,3), T(3,-3).
a. Foco (1.25,0); Parábola $$y^2\=3x$$; directriz $$x\=-3$$
b. Foco (0, 1.25); Parábola $$x^2\=3y$$; directriz $$y\=1.25$$
c. Foco (1.25, 0); Parábola $$y^2\=3x$$ ; directriz $$y\=3$$
d. Foco (0, 0.75); Parábola $$y^2\=3x$$ ; directriz $$x\=-0.75$$
4. Emplea la definición de la parábola para obtener una ecuación cartesiana de la parábola
con foco F(5,2) y directriz x=1.
a. $$10x\=y^2+4y+28$$
b. $$10x-y^2+4y+28\=0$$
c. $$8x\=y^2-4y+28$$
d. $$8x\=y^2+4y+28$$
5. Obtenga la ecuación de la parábola que pasa por los punto dados Q=(0,2), S=(1.5,-1) y T=(0.5,1)
a. $$y\=-2x^2+x+2$$
b. $$y\=2x^2-x+2$$
c. $$y\=-2x^2+x-2$$
d. $$x\=-2y^2+x+2$$
6. Un arco parabólico, tiene diez metros de altura, con el eje vertical y cuyos puntos de
apoyo están separados por 20m. ¿Está el foco de la parábola sobre el suelo o debajo de él,
y a qué distancia de la superficie está?
a. El foco está a 5.0 metros por abajo del suelo
b. El foco está a 7.5 metros por arriba del suelo
c. El foco está sobre el suelo
d. El foco está a 7.5 metros por abajo del suelo
7. Se tiene un reflector parabólico cuya forma se obtiene haciendo girar un arco de parábola
que empieza en el vértice, alrededor del eje de la parábola. Si el foco está a 9cm del
vértice y el arco parabólico tiene 16cm de profundidad. ¿Cuál es la abertura del reflector?
a. 40cm
b. 30cm
c. 48cm
d. 20cm
8. Hay que encerrar a un campo rectangular mediante una cerca de 120m de longitud. Si el
área es y cuando uno de los lados tiene longitud x, entonces y=60x - x^2. Trace la gráfica
de esta ecuación para x en [0,60] y determine el valor de x para que el área sea máxima.
65
a. $$x\=30m$$
b. $$x\=20$$
c. $$x\=25$$
d. $$x\=40$$
9. La hipérbola y la elipse cuyas ecuaciones son 3x^2-y^2=12 y
9x^2+25y^2=225,respectivamente, tienen los mismos focos cuyos valores son:
a. Los focos están en $$(-2,0)$$ y $$(2,0)$$
b. Los focos están en $$(-5,0)$$ y $$(5,0)$$
c. Los focos están en $$(-3,0)$$ y $$(3,0)$$
d. Los focos están en $$(-4,0)$$ y $$(4,0)$$
10. Dos observadores están en los puntos A(-5,0) y B(5,0), respectivamente. Un cañón se
encuentra en un lugar Q(x,6). El observador en A oye un disparo 18 segundos después del
momento en que lo oye el observador B. Encuentra la posición del cañón. Considera que
el sonido viaja a \frac{1}{3}km/s.
a. $$(3/4 \sqrt\{52\},6)$$ y $$ (-3/4 \sqrt\{52\},6)$$
b. $$ (3/4 \sqrt\{20\},6)$$ y $$ (-3/4 \sqrt\{20\},6)$$
c. $$ (3/4 \sqrt\{25\},6)$$ y $$ (-3/4 \sqrt\{25\},6)$$
d. $$ (3/4 \sqrt\{28\},6)$$ y $$ (-3/4 \sqrt\{28\},6)$$
Coordenadas polares
1. Si se tiene la siguiente ecuación polar, R=\frac{4}{4-8 \cos \alpha} ¿de qué curva se trata?
a. Parábola
b. Hipérbola
c. Elipse
d. Circunferencia
2. Elige el vector que corresponda a la suma de los vectores en coordenadas polares
u_\alpha=(2,30^\circ) y v_\alpha=(1,45^\circ).
a. $$(2.9772,34.98^\circ)$$
b. $$(8.8637,34.98^\circ)$$
c. $$(3,75^\circ)$$
d. 8.8637,14.987^\circ)$$
3. De las opciones siguientes elige la ecuación de una elipse.
a. $$R\=\frac\{6\}\{3+2 \cos \alpha\}$$
b. $$R\=\frac\{6\}\{3 \sin \alpha+2 \cos \alpha\}$$
c. $$R\=\frac\{6\}\{3 +6 \cos \alpha\}$$
d. $$R\=\frac\{1\}\{1 +6 \cos \alpha\}$$
4. Elige una ecuación polar que corresponda a la recta descrita por y=3x+1.
a. $$R\=\frac\{1\}\{\sin (t)-3 \cos (t)\}$$
b. $$R\=\frac\{1\}\{1-3 \cos (t)\}$$
c. $$R\=\frac\{1\}\{3 \sin (t)-3 \cos (t)\}$$
d. $$R\=3 \sin (t)-3 \cos (t)$$
66
5. ¿Qué lugar geométrico representa la ecuación polar R=3\sin \alpha -3 \cos \alpha?
a. Una circunferencia con centro fuera del origen.
b. Una recta
c. Una elipse con vértice en el origen.
d. Una elipse centrada en el origen.
6. Un vector en coordenadas polares esta descrito por u_\alpha=(3,120^\circ). Elige su
representación en coordenadas cartesianas
a. $$u\=(-\frac\{3\}\{2\},\frac\{3\sqrt\{3\}\}\{2\})$$
b. $$u\=(\frac\{1\}\{2\},-\frac\{\sqrt\{3\}\}\{2\})$$
c. $$u\=(\frac\{3\}\{2\},-\frac\{\sqrt\{3\}\}\{2\})$$
d. $$u\=(-\frac\{3\}\{2\},\frac\{\sqrt\{2\}\}\{2\})$$
7. Elige entre las opciones la ecuación polar de una parábola con foco en (0,0) y vértice en (1,0).
a. $$R\=\frac\{2\}\{1-\cos \alpha\}$$
b. $$R\=\frac\{-2\}\{1-\cos \alpha\}$$
c. $$R\=\frac\{1\}\{1-2 \cos \alpha\}$$
d. $$R\=\frac\{1\}\{1- \cos \alpha\}$$
8. La ecuación polar de una parábola está dada por: R=\frac{6}{3-3 \cos \alpha}, ¿Cuánto vale
su lado recto?
a. 4
9. Encuentra y captura el valor de la distancia focal de la elipse descrita por la ecuación polar:
R=\frac{4}{1-0.5 \cos \alpha}
a. 5.33
10. La excentricidad de la órbita que describe la tierra alrededor del sol es e=0.01671. Si su
perihelio vale 0.983 UA (unidades astronómicas) ¿cuánto vale su afelio?
a. 1.01641
Tangentes acónicas
1. Una cónica tiene como ecuación 4y^2-2x^2-2x+6y+5=0. Selecciona, entre las opciones la
que corresponda a la derivada de esta ecuación.
a. $$(8y+6)\frac\{dy\}\{dx\}-4x-2\=0$$
b. $$8y\frac\{dy\}\{dx\}-4x-2\=0$$
c. $$6\frac\{dy\}\{dx\}-4x-2\=0$$
d. $$(8y+6)y-4x-2\=0$$
2. Una hipérbola tiene como ecuación x y=1. Elige la ecuación de su tangente en el punto
P=(1,1).
a. $$x+y\=2$$
b. $$x-y\=0$$
c. $$0.5x-0.5y\=0$$
d. $$0.5x+0.5y\=-1$$
67
3. El punto de intersección (x,y) entre una recta y una cónica se puede resolver con la
ecuación m^2 x^2+2 m x+6 x-8=0. Elige entre las opciones la que contenga el
discriminante de esta ecuación para x.
a. $$12 (3 + 2 m + 3 m^2)$$
b. 12 (3 + 2 m )$$
c. $$3 + 2 m + 3 m^2$$
d. $$12$$
4. Elige la ecuación que corresponda a la recta tangente de la cónica x^{2}+3x+4y=0 en el
punto P=(0,0).
a. $$y\=-\frac\{3\}\{4\}x$$
b. $$y\=-\frac\{4\}\{3\}x$$
c. $$y\=\frac\{4\}\{3\}x$$
d. $$y\=\frac\{3\}\{4\}x$$
5. Elige las ecuaciones de las rectas que pasan por el punto S=(0,0) y son tangentes a la
parábola x=y^{2}+9.
a. $$y\=\frac\{1\}\{6\}x$$ e $$y\=-\frac\{1\}\{6\}x$$
b. $$y\=\frac\{1\}\{6\}x+2$$ e $$y\=-\frac\{1\}\{6\}x-2$$
c. $$x\=\frac\{1\}\{6\}y$$ e $$x\=-\frac\{1\}\{6\}y$$
d. $$x\=\frac\{1\}\{3\}y$$ e $$x\=-\frac\{1\}\{3\}y$$
6. Encuentra el punto en que se intersectan la recta y=6-x y la parábola y^2+6x-6y=0. Elige la
respuesta correcta.
a. $$(0,6)$$
b. $$(0,0)$$
c. $$(6,0)$$
d. $$(5/6,1)$$
7. Usando geogebra calcula en ángulo de intersección entre las curvas y^2+\frac{x^2}{9}=1 y
y^2+\frac{(x-3)^2}{9}=1. Captura el resultado, en grados, en el campo de respuesta.
a. 158.21
8. Captura el valor de la ordenada al origen b de la recta y=\frac{2}{3}x+b si esta es tangente
a la cónica x^{2}+4y^{2}-4x+6y=0.
a. 4.167
9. Captura el valor de la ordenada al origen b de la recta y=m x+b si esta es tangente a la
cónica y=4-x^2 y pasa por el punto P=(0,5).
a. 5
10. Captura el valor de la pendiente a la cónica x^{2}+y^{2}+3x+5y=0 en el punto P=(1,-4).
a. 1.667
Banco de preguntas Examen Diagnostico y Final
1. ¿A cuál de las siguientes figuras describe la ecuación x^2 /9 - y/4 = 1?:
68
a.
b.
c.
d.
e.
2. ¿Cuál de las ecuaciones en la lista representa correctamente a la parábola de la figura
siguiente?:
69
a. $$y\=x^2-4$$
b. $$y\=x^2+4$$
c. $$x\=-y^2+16$$
d. $$x\=y^2-16$$
e. $$y\=-x^2+4$$
3. ¿Cuánto vale la excentricidad e de la cónica representada por la ecuación 4 x^2+4 y^2 =3?
a. $$e\=1/2$$
b. $$e\=1$$
c. $$e\=0$$
d. $$e\=2$$
e. $$e\=-2$$
4. Determinar la ecuación, centro y radio de la circunferencia que pasa por los puntos (6,2),
(8,0), cuyo centro está sobre la recta 3x+7y+2=0:
70
a. $$(x-4)^2+(y+2)^2\=20$$
b. $$(x-2)^2+(y+4)^2\=20$$
c. $$(x-4)^2+(y-2)^2\=20$$
d. $$\sqrt[n]\{(x-4)\}+\sqrt[n]\{(y+2)\}\=20$$
e. $$(x-4)^2+(y-2)^2\=20^2$$
5. Determinar la ecuación de la circunferencia circunscrita al triángulo cuyos vértices son:
P_1(-1,1), P_2(3,5) y P_3(5,-3):
a.
b.
c.
d.
$$(x-\frac\{16\}\{5\})^2+(y-\frac\{4\}\{5\})^2\=\frac\{442\}\{25\}$$
$$(x+\frac\{16\}\{5\})^2+(y+\frac\{4\}\{5\})^2\=\frac\{442\}\{25\}$$
$$(x-\frac\{16\}\{5\})+(y-\frac\{4\}\{5\})\=\frac\{442\}\{25\}$$
$$\sqrt[]\{(x-\frac\{16\}\{5\})^2\}+\sqrt[]\{(y\frac\{4\}\{5\})^2\}\=\frac\{442\}\{25\}$$
e. $$(x-\frac\{4\}\{5\})^2+(y-\frac\{16\}\{5\})^2\=\frac\{442\}\{25\}$$
6. Determine la ecuación de la elipse con vértices (\pm 4,0) y focos (\pm 2,0):
a. $$3x^2 + 4y^2 \= 48$$
b. $$2x^2 + 4y^2 \= 48$$
c. $$2x^2 - 4y^2 \= 48$$
d. $$4y^2 - 2x^2 \= 48$$
e. $$4x^2 + 2y^2 \= 48$$
7. Determine la ecuación de una hipérbola que tiene las siguientes características. Vértices
son los puntos V(0,3) y V'(0,-3). Focos F(0,5) y F'(0,-5):
a. $$\frac\{y^2\}\{9\}-\frac\{x^2\}\{16\}\=1$$
b. $$\frac\{y^2\}\{16\}-\frac\{x^2\}\{9\}\=1$$
c. $$\frac\{y^2\}\{3\}-\frac\{x^2\}\{4\}\=1$$
d. $$\frac\{y^2\}\{9\}+\frac\{x^2\}\{16\}\=1$$
e. $$\frac\{y^2\}\{9\}-\frac\{x^2\}\{16\}\=0$$
8. ¿Cuál de los siguientes vectores representa a una ecuación paramétrica de la elipse:
a. $$(4\cos(t),2\sin(t))$$
b. $$(2\cos(t),2\sin(t))$$
c. $$(4\sec(t),2\tan(t))$$
d. $$(4\cos(t),4\sin(t))$$
e. $$(4\tan(t),2\sec(t))$$
71
9. ¿Qué ecuación describe la siguiente figura?:
a. $$r\=\frac\{10\}\{3+2 \cos \{\theta\}\}$$
b. $$r\=\frac\{10\}\{2+2 \cos \{\theta\}\}$$
c. $$r\=\frac\{10\}\{3+3 \cos \{\theta\}\}$$
d. $$r\=\frac\{-10\}\{3+2 \cos \{\theta\}\}$$
e. $$r\=\frac\{10\}\{3+2 \cos \{2\theta\}\}$$
10. ¿Cuál de las siguientes opciones contiene la ecuación de la recta que se muestra en la
figura?
a. $$y\=-2x-\frac\{1\}\{2\}$$
b. $$y\=x+\frac\{1\}\{2\}$$
c. $$y\=-\frac\{1\}\{2\}x+\frac\{1\}\{2\}$$
d. $$y\=\frac\{1\}\{2\}x+1$$
e. $$y\=\frac\{1\}\{2\}x-1$$
11. ¿Cuál de las siguientes opciones contiene la ecuación de la recta que se muestra en la
figura?
72
12.
13.
14.
15.
a. $$y\=2x-1$$
b. $$y\=3x+1$$
c. $$y\=2x+1$$
d. $$y\=\frac\{1\}\{2\}x+1$$
e. $$y\=\frac\{1\}\{2\}x-1$$
¿Cuánto vale la distancia del punto A=(0,1) a la recta y=x?
a. $$1$$
b. $$\sqrt\{2\}$$
c. $$1/\sqrt\{2\}$$
d. $$1/2$$
e. $$\sqrt\{3\}/2$$
Determinar la ecuación de la mediatriz (perpendicular en su punto medio) del segmento (2,1), (3,-5):
a. $$10x-12y-29\=0$$
b. $$10x+12y+29\=0$$
c. $$y-2\=\frac\{5\}\{6\}(x+\frac\{1\}\{2\})$$
d. $$10x+12y-29\=0$$
e. $$y+2\=\frac\{6\}\{5\}(x+\frac\{1\}\{2\})$$
Determinar la ecuación de la recta que pasa por el punto (-3,1) y es paralela a la recta
determinada por los dos puntos (0,-2) y (5,2):
a. $$4x-5y+17\=0$$
b. $$4x+5y-17\=0$$
c. $$4x-5y-17\=0$$
d. $$-4x-5y+17\=0$$
e. $$4x+5y+17\=0$$
Determinar la ecuación de la recta que pasa por el punto (4,-1) y tiene ángulo de
inclinación de 135^o:
a. $$x+y-3\=0$$
b. $$x+y+3\=0$$
c. $$-x+y-3\=0$$
d. $$x-y-3\=0$$
e. $$-x-y-3\=0$$
73
16. El interior de una antena de TV por satélite es un disco con forma paraboloide (finito) de
diámetro de 12 pies y profundidad de 2 pies. Encuentra la distancia desde el centro del
disco hasta el foco.
a. $$4.5 pies$$
b. $$3 pies$$
c. $$3 metros$$
d. $$6 pies$$
e. $$2.5 pies$$
17. En una red se encuentran una araña y una cucaracha como se muestra en la figura. Cada
nudo de la red se separa de otro por 1 cm. ¿A qué distancia se encuentra la araña de la
cucaracha?
a. $$\sqrt[]\{85\}$$7
b. $$\sqrt[]\{70\}$$
c. $$\sqrt[]\{49\}$$
d. $$\sqrt[]\{13\}$$
e. $$\sqrt[]\{90\}$$
18. En un parque hay un pequeño lago artificial circular, el cual se describe por la ecuación
x^2+y^2=30m. Si un pato está en la coordenada (6m,4m) se puede afirmar que:
a. El pato está afuera del lago
b. El pato está adentro del lago
c. El pato está en el centro del lago
d. El pato está cerca del centro del lago
e. El pato está en la orilla del lago
19. La base de un auditorio es de forma elíptica, tiene 20 metros de longitud y 16 metros de
ancho. Si cae una aguja sobre un foco, ¿a qué distancia está un foco del otro foco?
a. está a $$12$$ metros
b. está a $$20$$ metros
c. está a $$16$$ metros
d. está a $$4$$ metros
e. está a $$6$$ metros
20. ¿Cuál es el valor exacto del \cos 30^\circ?
a. $$\frac\{1\}\{2\}$$
b. frac\{2\}\{\sqrt\{3\}\}$$
c. $$\frac\{\sqrt\{2\}\}\{2\}$$
d. $$\frac\{\sqrt\{3\}\}\{2\}$$
74
21.
22.
23.
24.
25.
26.
27.
e. $$\frac\{1\}\{\sqrt\{2\}\}$$
¿Cuál es el valor exacto del \cos 45^\circ?
a. $$\frac\{1\}\{2\}$$
b. $$\frac\{2\}\{\sqrt\{3\}\}$$
c. $$\frac\{\sqrt\{2\}\}\{3\}$$
d. $$\frac\{\sqrt\{3\}\}\{2\}$$
e. $$\frac\{1\}\{\sqrt\{2\}\}$$
¿Cuál es el valor exacto del \sin 30^\circ?
a. $$\frac\{1\}\{2\}$$
b. $$\frac\{2\}\{\sqrt\{3\}\}$$
c. $$\frac\{\sqrt\{2\}\}\{2\}$$
d. $$\frac\{\sqrt\{3\}\}\{2\}$$
e. $$\frac\{1\}\{\sqrt\{2\}\}$$
¿Cuál es el valor exacto del \sin 60^\circ?
a. $$\frac\{1\}\{2\}$$
b. $$\frac\{2\}\{\sqrt\{3\}\}$$
c. $$\frac\{\sqrt\{2\}\}\{2\}$$
d. $$\frac\{\sqrt\{3\}\}\{2\}$$
e. $$\frac\{1\}\{\sqrt\{2\}\}$$
El ángulo de inclinación respecto a la horizontal del vector B=(-1,1) es:
a. $$60^\circ$$
b. $$90^\circ$$
c. $$135^\circ$$
d. $$180^\circ$$
e. $$0^\circ$$
El producto punto entre los vectores A=(2,-5) y B=(1,-2) vale:
a. $$A \cdot B\=12$$
b. $$A \cdot B\=(3,-7)$$
c. $$A \cdot B\=12$$
d. $$A \cdot B\=(2,10) $$
e. $$A \cdot B\=-8$$
El tamaño del vector C=(1,0) es:
a. $$|A|\=1$$
b. $$|A|\=2$$
c. $$|A|\=\sqrt\{2\}$$
d. $$|A|\=\sqrt\{4\}$$
e. $$|A|\=1/2$$
El tamaño del vector A=(1,1) es:
a. $$|A|\=1$$
b. $$|A|\=2$$
c. $$|A|\=\sqrt\{2\}$$
d. $$|A|\=\sqrt\{4\}$$
75
28.
29.
30.
31.
32.
33.
34.
e. $$|A|\=1/2$$
Encuentra la ecuación de la elipse con centro en el origen, foco F(3,0) y excentricidad
e=0.6.
a. $$\displaystyle\{\frac\{x^2\}\{25\}+\frac\{y^2\}\{16\}\=1\}$$
b. $$\displaystyle\{\frac\{x^2\}\{16\}+\frac\{y^2\}\{25\}\=1\}$$
c. $$\displaystyle\{\frac\{x^2\}\{25\}+\frac\{y^2\}\{9\}\=1\}$$
d. $$\displaystyle\{\frac\{x^2\}\{3\}+\frac\{y^2\}\{9\}\=1\}$$
Encuentra la excentricidad de la elipse cuya ecuación es 3x^2+2y^2-18=0.
e. $$\displaystyle\{e\=\frac\{1\}\{\sqrt\{3\}\}\}$$
f. $$\displaystyle\{e\=\frac\{1\}\{0.58\}\}$$
g. $$\displaystyle\{e\=\frac\{1\}\{\sqrt\{9\}\}\}$$
h. $$\displaystyle\{e\=\frac\{\sqrt\{3\}\}\{\sqrt\{9\}\}\}$$
Si se tienen los siguientes vectores A=(2,2), B=(1/2,1/2) y C=(1,3), ¿Cuál será el valor de
(A\cdot B)\cdot C?
i. $$(1,3)$$
j. $$(2,6)$$
k. $$8$$
l. $$4$$
m. $$(1,1)$$
Se tienen tres vectores en el plano, dados por: A=(1,1), B=(0,1) y C=(0,-2). El vector D=3 AB+\frac{1}{2}C es:
n. $$(1,0)$$
o. $$(1,4)$$
p. $$(3,1)$$
q. $$(3,-1)$$
r. $$(1,-3)$$
Se tiene el vector A=(1,-4). Si B es un vector perpendicular a A, entonces:
s. $$B\=(2,-8)$$
t. $$B\=(-4,1)$$
u. $$B\=(-1,4)$$
v. $$B\=(4,1)$$
w. $$B\=(1,1)$$
La suma de los vectores en el plano, dados por A=(-1,1), B=(0,3) y C=(2,-1) es:
x. $$(1,-3)$$
y. $$(3,-1)$$
z. $$(-1,3)$$
aa. $$(-1,-3)$$
bb. $$(1,3)$$
¿Qué ángulo respecto al horizonte tendrá el sol cuando un objeto proyecta una sombra
del mismo largo que su altura?
cc. $$30^\circ$$
dd. $$45^\circ$$
76
ee. $$60^\circ$$
ff. $$90^\circ$$
gg. $$0^\circ$$
35. En la figura, el área del triángulo ABC es 60. Si la medida de DB es la tercera parte de la
medida CB, entonces el área del triángulo ADB es:
hh. 20
ii. 30
jj. 40
kk. 45
ll. 50
36. En el triángulo de la figura, la razón \frac{3}{4} expresa el valor de:
mm.
$$\sin u$$
nn. $$\cos u$$
oo. $$\tan u$$
pp. $$\cot u$$
qq. $$\sec u$$
37. El valor exacto del \cos(15^\circ) es:
rr. $$\frac\{1\}\{2\sqrt\{2\}\}$$
ss. $$\frac\{1+\sqrt\{3\}\}\{2\sqrt\{2\}\}$$
tt. $$\frac\{\sqrt\{3\}\}\{2\}$$
uu. $$\frac\{1+\sqrt\{2\}\}\{2\}$$
vv. $$\frac\{1\}\{2\}$$
38. Un albañil quiere dibujar una circunferencia en un terreno. Para ello, entierra un poste en
(0,0) y sujeta un lazo en el poste para hacer un radio hasta (2,4). ¿Cuál es la ecuación de la
circunferencia?
ww.
$$x^2+y^2\=20$$
77
xx. $$x^2+y^2\=8$$
yy. $$x^2+y^2\=16$$
zz. $$x^2+y^2\=24$$
aaa.
$$x^2+y^2\=25$$
39. ¿Qué ecuación podría describir la superficie de una rampa vista transversalmente? La base
mide 2 metros y su altura 1 metro.
40.
41.
42.
43.
bbb.
$$y\=\frac\{1\}\{2\}x$$
ccc. $$y\=2x$$
ddd.
$$y\=x$$
eee.
$$y\=2x+1$$
fff. $$y\=2x-1$$
La órbita que describe la Tierra alrededor del Sol es aproximadamente una elipse, con el
Sol en uno de sus focos. Si el eje mayor de la órbita elíptica es de 300000 km, y la
excentricidad es de 0.017 aproximadamente. Hallar la distancia máxima de la Tierra al Sol.
ggg.
$$152550 km$$
hhh.
$$3853493 km$$
iii. $$1534521 km$$
jjj. $$532558 km$$
kkk.$$987982558 m$$
La órbita que describe la Tierra alrededor del Sol es aproximadamente una elipse, con el
Sol en uno de sus focos. Si el eje mayor de la órbita elíptica es de 300000 km, y la
excentricidad es de 0.017 aproximadamente. Hallar la distancia mínima de la Tierra al Sol.
lll. $$147450 km$$
mmm.
$$183431 m$$
nnn.
$$980678 km$$
ooo.
$$675890 m$$
ppp.
$$89787 km$$
Un triángulo tiene sus vértices en los puntos A=(2,3), B=(6,9) y C=(8,1). ¿Cuál es la
coordenada su baricentro?
qqq.
$$(4,6)$$
rrr. $$\left(\frac\{16\}\{3\},\frac\{13\}\{3\}\right)$$
sss. $$\left(\frac\{65\}\{11\},\frac\{52\}\{11\}\right)$$
ttt. $$\left(\frac\{13\}\{3\},\frac\{16\}\{3\}\right)$$
uuu.
$$\left(\frac\{52\}\{11\},\frac\{65\}\{11\}\right)$$
Un triángulo tiene sus vértices en los puntos A=(0,0), B=(1,0) y C=(1/2,\sqrt{3}/2). ¿Cuánto
vale su perímetro?
vvv.1
78
www.
$$1/2$$
xxx. $$3/4$$
yyy.
3
zzz. 4
44. ¿Cuál de las siguientes opciones contiene la ecuación que describe a una recta
perpendicular a otra, dada por la ecuación 4x-3y=6?
aaaa.
$$4x+3y\=6$$
bbbb.
$$4x-3y\=-6$$
cccc.
$$3x-4y\=-6$$
dddd.
$$3x-4y\=6$$
eeee.
$$3x+4y\=6$$
45. ¿Cuál de las siguientes opciones contiene la ecuación que describe a una recta paralela a
otra dada por la ecuación 4x-3y=6?
ffff. $$4x+3y\=6$$
gggg.
$$-4x-3y\=-6$$
hhhh.
$$8x+6y\=-6$$
iiii. $$8x+6y\=6$$
jjjj. $$8x-6y\=6$$
46. Suponga que usted tiene un terreno plano de la siguiente forma y requiere pasar un tubo
de PVC por debajo del terreno que conecte el punto A con el punto B. ¿Cuál es la longitud
mínima que debe tener el tubo?:
kkkk.
$$d_\{min\}\=\sqrt[]\{(7+5)^2+(12+9)^2\}$$
llll. $$d_\{min\}\=\sqrt[]\{(7-5)^2+(12-9)^2\}$$
mmmm. $$d_\{min\}\=\sqrt[]\{(7+5)^2+(-18+4)^2\}$$
nnnn.
$$d_\{min\}\=\sqrt[]\{(7+5)^2+(18+4)^2\}$$
oooo.
$$d_\{min\}\=\sqrt[]\{(7-5)^2+(18+4)^2\}$$
47. En un círculo de centro en el origen y radio igual a 5, determinar la forma normal de la
ecuación de su tangente en el punto (-3,4):
79
48.
49.
50.
51.
pppp.
$$\frac\{-3\}\{5\}x+\frac\{4\}\{5\}y-5\=0$$
qqqq.
$$\frac\{3\}\{5\}x+\frac\{4\}\{5\}y-5\=0$$
rrrr.
$$\frac\{-3\}\{5\}x+\frac\{-4\}\{5\}y-5\=0$$
ssss.
$$\frac\{3\}\{5\}x+\frac\{4\}\{5\}y-5\=0$$
tttt. $$\frac\{3\}\{5\}x+\frac\{4\}\{5\}y+5\=0$$
¿En qué punto se intersectan las siguientes rectas?: y=3x+2, y=-5x-2
uuuu.
$$(0,0)$$
vvvv.
$$(1,1)$$
wwww.
$$(1/2,1/2)$$
xxxx.
$$(-1/2,1/2)$$
yyyy.
$$(-1,1/2)$$
Determinar los valores que deben tener los coeficientes de la ecuación general Ax+By+C=0
de una recta, para que pase por los dos puntos (-1,4) y (3,-2). Determinar la ecuación de la
recta:
zzzz.
Los coeficientes son $$A\=3, B\=2, C\=-5$$ y la ecuación es $$3x+2y5\=0$$
aaaaa.
Los coeficientes son $$A\=-3, B\=2, C\=-5$$ y la ecuación es $$-3x+2y5\=0$$
bbbbb.
Los coeficientes son $$A\=2, B\=3, C\=-5$$ y la ecuación es $$2x+3y5\=0$$
ccccc.
Los coeficientes son $$A\=3, B\=-2, C\=-5$$ y la ecuación es $$3x-2y5\=0$$
ddddd.
Los coeficientes son $$A\=-3, B\=2, C\=5$$ y la ecuación es $$3x+2y+5\=0$$
Sea C una curva con ecuaciones paramétricas x=t^3-3t; y=t^2-5t-1, donde t está en R.
Encuentre una ecuación de la recta tangente a C en el punto correspondiente a t=2:
eeeee.
$$y+7\=\frac\{-1\}\{9\}(x-2)$$ o su equivalente $$x+9y+61\=0$$
fffff.
$$y+7\=\frac\{1\}\{9\}(x-2)$$ o su equivalente $$x+9y\=61$$
ggggg.
$$y+7\=\frac\{+1\}\{9\}(x-2)$$
hhhhh.
$$y-7\=\frac\{+1\}\{9\}(x-2)$$
iiiii. $$y+7\=\frac\{1\}\{9\}(x-2)$$
¿Qué ecuación describe la siguiente figura (rosa de cuatro pétalos)?
80
52.
53.
54.
55.
jjjjj. $$r\=a \sin\{20\}$$, donde $$a>0$$
kkkkk.
$$r\=-2a \cos\{20\}$$, donde $$a>0$$
lllll. $$r\=-a \sin\{20\}$$, donde $$a>0$$
mmmmm. $$r\=2a \cos\{20\}$$, donde $$a>0$$
nnnnn.
$$r\=\frac\{1\}\{2\}a \cos\{20\}$$, donde $$a>0$$
Una circunferencia representada por la ecuación (x-3)^2+(y+1)^2=9 tiene su centro en:
ooooo.
$$(-3,1)$$
ppppp.
$$(3,1)$$
qqqqq.
$$(-1,3)$$
rrrrr.
$$(3,-1)$$
sssss.
$$(-3,-1)$$
Los vértices de la hipérbola representada por la ecuación \frac{x^2}{16}-\frac{y^2}{9}=1
son:
ttttt.
$$(0,-4)$$ y $$(0,4)$$
uuuuu.
$$(0,3)$$ y $$(0,-3)$$
vvvvv.
$$(-16,0)$$ y $$(9,0)$$
wwwww. $$(-4,0)$$ y $$(4,0)$$
xxxxx.
$$(-3,0)$$ y $$(4,0)$$
La relación x^2+y^2=9 representa:
yyyyy.
Una parábola con vértice en el origen y foco en $$(3,0)$$.
zzzzz.
Una circunferencia de radio $$3$$ y centro en el origen.
aaaaaa.
Una circunferencia de radio $$9$$ y centro en el origen.
bbbbbb. Una elipse centrada en el origen con semieje mayor igual a $$9$$.
cccccc.
Una parábola con vértice en el origen y foco en $$(0,3)$$.
La elipse de la figura siguiente se representa por la ecuación:
81
dddddd. $$x^2 /4 + y^2/9 \= 1$$
eeeeee. $$x^2 /2 + y^2/3 \= 1$$
ffffff.
$$x^2 /3 + y^2/2 \= 1$$
gggggg.
$$3 x^2 + 2 y^2 \= 1$$
hhhhhh. $$x^2 /9 + y^2/4 \= 1$$
56. La ecuación que representa la siguiente gráfica es:
iiiiii.
$$2x\=y^2+8y+22$$
jjjjjj.
$$2x\=y^2-8y+22$$
kkkkkk.
$$2x\=x^2+8x+22$$
llllll.$$x\=y^2+8y+22$$
mmmmmm.
$$2x\=y^2-8y+22$$
57. La ecuación de una circunferencia con centro en el origen y diámetro igual a 8 se
representa por la ecuación:
nnnnnn. $$x^2+y^2\=8$$
oooooo. $$x^2+y^2\=\sqrt\{8\}$$
pppppp. $$x^2+y^2\=16$$
qqqqqq. $$x^2+y^2\=64$$
rrrrrr.
$$x^2+y^2\=4$$
58. Determine una ecuación para la parábola con vértice en (4,-1), eje paralelo al eje y y que
pasa por el origen:
ssssss.
$$(x-4)^2\=16(y+1)$$
tttttt.
$$(x-4)^2\=16(y+1)^2$$
82
uuuuuu. $$(x-4)^2\=16(y-1)$$
vvvvvv.
$$(x-1)^2\=16(y+4)$$
wwwwww. $$(x-1)^2\=16(y-1)$$
83
Ejercicios
Vectores
1. Se tiene un vector u=(3,2), ¿ Cuáles son las coordenadas al que apunta este vector si comienza
del punto A=(-1,2) ?
a. El punto final queda en (2,4).
b. El punto final queda en (4,4).
c. El punto final queda en (4,0).
2. ¿Cuáles son las coordenadas del punto final de un vector v=(3,-2) si tiene como punto inicial
A=(-1,2).
a. (3,-2)
b. (-2,-2)
c. (2,2)
3. Dos pares ordenados (a,b) y (c,d), ya sea que representen un punto o un vector son iguales
entre si sólo si cumplen que a=c y b=d. De esta manera encuentra que valores de x e y
cumplen que: (x-2y,2x+y)=(-1,3).
a. x=-1, y=-1
b. x=1, y=1
c. x=\frac{7}{5}, y=\frac{1}{5}
4. En la siguiente construcción se tiene un vector que va del punto Q al punto R. ¿A qué punto
llegaría este mismo vector si empezará del punto S?
a. (6,2)
b. (-1,-2)
c. (5,-4)
5. Se tiene un punto indeterminado P=(x,y), pero que cumple la condición de que el vector que
va del punto A=(-1,-2) a P es igual que el vector que va de B=(2,4) a C=(8,-2). Determina las
coordenadas de P y elige la opción correcta.
a. P=(7,-8)
b. P=(5,-8)
c. P=(5,-4)
84
6. Se tienen los siguientes vectores: u=(0,1), v=(3,2) y w=(-1,4). De las opciones siguientes elige
un vector t, tal que verifique la relación: w+v=t-u
a. t=(2,7)
b. t=(2,5)
c. t=(-4,3)
7. En la siguiente construcción se tienen los puntos A, B , C y D. Si se trazan cuatro vectores entre
ellos, el primero del punto A al B, el segundo de B a C, el tercero de C a D y el último de D a A,
¿cuánto vale el vector suma de estos cuatro?
8.
9.
10.
11.
a. (0,0)
b. (0,1)
c. (-1,0)
Imagina que un avión se mueve desde su punto de despegue en línea recta recorriendo 300
Km hacia el este y 100 Km hacia el norte de su punto de partida. En ese punto vira y después
de cierto tiempo, se desplaza a partir de ese punto otros 100 Km al norte y 50 Km hacia el
oeste. ¿A qué distancia se encuentra el avión del punto de partida?
a. 320.16km
b. 403.11km
c. 206.155km
Una persona inicia un viaje en automóvil y llega a su destino situado a 100Km al sur. La
carretera que tomó pasa por una población situada a 30Km al este y 10Km al sur del punto de
partida. ¿Qué distancia, en línea recta, hay del poblado al destino final del viajero?
a. distancia=94.86 Km
b. distancia=114.02 Km
c. distancia=130.38 Km
Un triángulo tiene sus vértices en los puntos A=(1,2), B=(-1,2) y C=(0,-4). De entre las opciones
de abajo, escoge la que contenga tres vectores que representen los lados del triángulo y el
valor de su perímetro.
a. Vectores: (2,0), (-1,6) y (-1,-6), Perímetro: 14.1655.
b. Vectores: (0,4), (-1,-2) y (1,-2), Perímetro: 8.47214.
c. Vectores: (1,2), (-1,2) y (0,-4), Perímetro: 8.47214.
Tenemos dos vectores, u=(1,2) y v=(3,1), analicen la siguiente operación, si tomamos los
siguientes valores de t: t=-1, t=1 y t=\frac{1}{2}: w=u+ t v. Los valores de w correspondientes
son:
85
a. w=(-2,1), w=(4,3), w=(\frac{5}{2},\frac{5}{2})
b. w=(2,-1), w=(-4,-3), w=(\frac{5}{2},\frac{5}{2})
c. w=(2,1), w=(4,-3), w=(-\frac{5}{2},\frac{5}{2})
12. ¿Por qué escalar t hay que multiplicar un vector u=(3,-2) para obtener el vector v=(-1,2/3)?
a. t=-\frac{1}{3}
b. t=3
c. No existe el valor porque no apuntan en la misma dirección.
13. Se tiene un vector u=(3,2) en la construcción que se muestra. Utilizando la barra deslizadora,
encuentra el valor de t necesario para que el tamaño del vector w=t u sea aproximadamente
1. Calcula el valor exacto de t utilizando las propiedades de los vectores. ¿Cuáles son los
valores de t encontrados?
a. Valor aproximado: t=0.27. Valor exacto: t=0.27
b. Valor aproximado: t=0.28. Valor exacto: t=\frac{1}{\sqrt{13}}
c. Valor aproximado: t=0.56. Valor exacto: t=\frac{2}{\sqrt{13}}
14. Tenemos un vector v=(4,2), de las opciones siguientes, escoge un vector w que sea unitario y
que apunte en la misma dirección de v.
a. w=(\frac{2}{\sqrt{5}},\frac{1}{\sqrt{5}})
b. w=(\frac{1}{\sqrt{5}},\frac{2}{\sqrt{5}})
c. w=(-\frac{1}{\sqrt{5}},-\frac{2}{\sqrt{5}})
15. Como se mencionó en las definiciones, un vector es perpendicular a otro si su producto punto
es igual a cero, pues esto indica que el ángulo entre ellos es de 90^\circ (o \pi/2 radianes). En
la siguiente construcción, encuentra un vector perpendicular a u=(1.5,1) usando los vectores
i=(1,0) y j=(0,1) y las operaciones vectoriales (producto punto, producto escalar y suma de
vectores). ¿Cuál de las siguientes expresiones es adecuada para esta relación y cuál es el valor
de un vector perpendicular a u?
86
a. Expresión: (u \cdot j) i + (u \cdot i) j. Valor: (1,1.5).
b. Expresión: -(u \cdot j) i + (u \cdot i) j. Valor: (-1,1.5).
c. Expresión: (u \cdot i) i + (u \cdot j) j. Valor: (1.5,1).
Puntos y rectas
1. Si A(8,10) y B(4,2) son puntos extremos del Segmento dirigido AB. Hallar las coordenadas del
punto C(x,y) que divide a este segmento en la razón AC/CB=\frac{2}{3}.
a. C(6,6)
b. C(\frac{32}{5},\frac{34}{5})
c. C(\frac{64}{5},\frac{40}{5})
2. Si A(5,0) y B(-1,3) son puntos extremos del Segmento dirigido AB. ¿Cuáles son las coordenadas
del punto C(x,y) que divide a este segmento en la razón AC/CB=-4?
a. C(-3,4)
b. C(\frac{2}{-3},\frac{1}{-3})
c. C(1,2)
87
Lugares geométricos I
1. Obtenga y seleccione la ecuación cartesiana del lugar geométrico de todos los puntos H=(x,y)
tales que la pendiente del segmento que conecta a cada punto de H con S=(1,1) es la mitad de
la pendiente del segmento que los conecta con T=(2,5).
a. y=\frac{1-3x}{x+3}
b. y=\frac{x+3}{x-3}
c. y=\frac{1+3x}{x-3}
2. Calcula y elige la ecuación que representa el lugar geométrico de los puntos cuyas distancias a
la recta definida por la ecuación cartesiana y=x y al punto F=(-1,1) son siempre iguales.
a. 2 + 2 x + \frac{x^2}{2} - 2 y + x y + \frac{y^2}{2}=0
b. 2 + 2 x - 2 y + 2 x y=0
c. 2 + 2 x + \frac{x^2}{2} - 2 y - x y + \frac{y^2}{2}=0
3. Obtenga una ecuación cartesiana del lugar geométrico de los puntos tales que el segmento
que va de cualquier punto de P=(x,y) a A=(-2,0) es perpendicular al segmento que va del punto
a B=(2,0).
a. x^{2}+ y^{2}=4
b. x + y=4
c. x^2 + y^2 =2
4. Una circunferencia pasa por los puntos A=(0,0), B=(7,0) y C=(3.5,3). Usando geogebra
determina la ecuación cartesiana de la circunferencia que pasa por ellos.
a. (x-3.5)^2+(y+0.54)^2=12.54
b. (x-3.5)^2+(y+0.04)^2=12.25
c. (x-0.04)^2+(y-3.5)^2=12.25
5. Determina y elige el centro y el radio de la circunferencia descrita por la ecuación cartesiana
x^2+y^2+4x-9y=0
a. Centro=(-2,4.5), Radio=4.92
b. Centro=(2,-4.5), Radio=24.25
c. Centro=(2,4.5), Radio=24.25
6. Elije la ecuación vectorial de la recta que es tangente en el punto A=(6,-4) a la circunferencia
cuya ecuación es: x^{2}+y^{2}-4x+2y-20=0
a. (x,y)=(6,-4)+t(3,4)
b. (x,y)=(6,-4)+t(-3,4)
c. (x,y)=(2,-1)+t(4,-3)
7. Determinación de los focos de la elipse. Se tiene una elipse descrita por la ecuación:
\begin{displaymath} \frac{x^2}{4}+\frac{y^2}{25}=1, \end{displaymath} por lo que su centro
está en (0,0) y sus semiejes valen a=2 y b=5. ¿Cuánto valen las coordenadas de los focos de la
elipse?
a. F1=(0,\sqrt{21}) y F2=(0,-\sqrt{21})
b. F1=(\sqrt{21},0) y F2=(-\sqrt{21},0)
c. F1=(\sqrt{25},0) y F2=(-\sqrt{25},0)
88
8. El lado recto de una elipse es un segmento que se forma con los dos puntos de intersección de
la elipse con una recta perpendicular al eje mayor que pasa por un foco. Traducido a un dibujo
esta definición se muestra en la figura que sigue, donde los lados rectos se trazaron en color
rojo:
Es claro que toda elipse tiene dos lados rectos cuyo tamaño es igual. El problema dice así:
¿cuánto vale el tamaño del lado recto de una elipse descrita por la ecuación:
\begin{displaymath} \frac{x^2}{36}+\frac{y^2}{16}=1 \end{displaymath}?
a. 16/3
b. 8/3
c. 4/2
9. Escoge el valor del lado recto de una elipse que tiene focos en (2,2) y (5,2) y tiene un vértice
en (0,2).
a. 5.71
b. 2.85
c. 11.42
Lugares geométricos II
1. ¿Cuál es la ecuación de la parábola con vértice en el origen y foco F(2,0), y cuál es la ecuación
de su directriz?
a. Parábola: y^2=8x, Directriz: x=-2.
¿Cómo se hace?
Sabemos que:
\left|\left(x,y\right)-\left(2,0\right)\right|=\left|\left(x,y\right)-\left(-2,y\right)\right|,
\left|\left(x-2,y\right)\right|=\left|\left(x+2,0\right)\right|,
\sqrt{\left(x-2\right)^2+\left(y\right)^2}=\sqrt{\left(x+2\right)^2},
\left(x-2\right)^2+y^2}=\left(x+2\right)^2,
4-4x+x^2+y^2= 4+4x+x^2,
y^2=8 x.
89
2. Calcule las coordenadas del foco, obtenga una ecuación cartesiana de la directriz y de la
parábola con vértice en el origen y que pasa por los puntos S(-5,5), T(-5,-5).
a. Parábola: y^2=-5x, Directriz: x=1.25
¿Cómo se hace?
Al graficar S y T nos damos cuenta que el eje de la parábola debe ser el eje x, y como la
parábola tiene vértice en el origen, entonces debe abrir hacia la izquierda. Por lo que
sabemos que su ecuación es de la forma y^2=4px. Por lo tanto la parábola tiene foco
F\left(\frac{-25}{20},0\right) y directriz x=\frac{25}{20}. De donde se deduce que su
ecuación es y^2=-5x.
3. Emplea la definición de la parábola para obtener una ecuación cartesiana de la parábola con
foco F(-2,-5) y directriz y=-4.
a. Parábola: x^2=-4x-2y-13.
¿Cómo se hace?
Un punto U(x,y) está sobre la parábola si:
|u-f|=|u-w|
|(x,y)-(-2,-5)|=|(x,y)-(x,-4)|,
|(x+2,y+5)|=|(x-x,y+4)|,
\sqrt{(x+2)^2+(y+5)^2} =\sqrt{(y+4)^2},
(x+2)^2+(y+5)^2}=(y+4)^2,
4+4x+x^2+25+10y+y^2=16+8y+y^2,
90
x^2=-4x-2y-13.
4. Cuando se arroja una piedra desde un punto A, la piedra viaja aproximadamente a lo largo de
un arco parabólico con eje vertical. Si se arroja la piedra en una dirección que forma un ángulo
de 45^\circ con la horizontal, entonces el foco de la parábola está sobre una recta horizontal
que pasa por A.
Supongamos que una piedra que se lanza con este ángulo de elevación llega a una altura
máxima de 40m. ¿Qué distancia recorre la piedra horizontalmente hasta el momento de
alcanzar una altura igual a la del punto A?
a. 80m.
¿Cómo se hace?
Primero notemos que lo que deseamos es calcular la distancia entre los puntos A y B. Este
segmento que es perpendicular al eje focal de la parábola, cuyo punto medio es el foco y
cuyos extremos A y B, están sobre la parábola es el lado recto, y su longitud se llama ancho
focal y mide |4p|. De esta manera. La ecuación de la parábola que describe la piedra
lanzada es x^2=4py, donde p<0. Entonces en y=p, x=\pm|2p|, por lo que la distancia
entre A y B, la distancia horizontal que recorre la piedra es de 160m.
5. Calcula la ecuación de la hipérbola con focos F1(0,5) y F2(0,-5); y con vértices V1(0,4) y V2(0,4).
a. \displaystyle{\frac{y^2}{16}-\frac{x^2}{9}=1}.
¿Cómo se hace?
91
Observando la figura notamos que un punto U con coordenadas (x,y) está sobre la
hipérbola si cumple con:
\left\|U-F1\right\|-\left\|U-F2\right\|=2ª
\left\|\left(x,y\right)-\left(0,5)\right\|-\left\|\left(x,y\right)-\left(0,-5\right)\right\|=8
\left\|\left(x,y-5\right)\right\|-\left\|\left(x,y+5\right)\right\|=8
\sqrt{x^2+\left(y-5\right)^2}-\sqrt{x^2+\left(y+5\right)^2}=8
Con un poco de álgebra obtenemos que la ecuación es:
\displaystyle{\frac{y^2}{16}-\frac{x^2}{9}=1}
6. Obtén la ecuación de la hipérbola con centro en el origen y cuya longitud del eje conjugado es
2a=10, y del eje transversal es 2b=8, y con eje principal el eje x.
a. \displaystyle{\frac{x^2}{25}-\frac{y^2}{16}=1}.
¿Cómo se hace?
Puesto que la longitud del eje conjugado es 10, la parábola tiene su centro en el origen y
eje principal el eje x, las coordenadas de sus vértices son: (-5,0) y (5,0). Por otra parte
sabemos que la longitud del eje transversal es 8, por lo que b=4. Por tanto la ecuación es:
\frac{x^2}{25}-\frac{y^2}{16}=1. La hipérbola se ve como en la figura.
7. Calcula las coordenadas de los vértices y los focos de la hipérbola con ecuación \frac{x2}{25} \frac{y2}{9}=1.
a. De la ecuación deducimos que a=5 y b=3. Por lo que las coordenadas de los vértices
son (-5,0) y (5,0). Por otra parte, como c^2=b^2-a^2, entonces c^2=34, y las
coordenadas de los focos son (-\sqrt{34},0) y (\sqrt{34},0).
92
8. Obtén la ecuación cartesiana de la hipérbola con centro en el origen, cuyos focos son F1(4,0) y
F2(-4,0), y que pasa por el punto S(14,24).
a. \displaystyle{\frac{x^2}{4}-\frac{y^2}{12}=1}.
¿Cómo se hace?
Sabemos que:
\left\|u-f1\right\|-\left\|u-f2\right\|=2ª
\left\|(14,24)-(4,0)\right\|-\left\|(14,24)-(-4,0)\right\|
\left\|(10,24)\right\|-\left\|(18,24)\right\|=4
Por lo tanto a=2. Por otra parte sabemos que: b^2=c^2-a^2, y de las coordenadas de los
focos sabemos que c=4. Por lo tanto b^2=c^2-a^2=16-4=12. De donde concluimos que la
ecuación de la hipérbola es: : \frac{x^2}{4}-\frac{y^2}{12}=1.
Coordenadas Polares
1. Se tiene un vector u=(1,-1), ¿Cuál es su representación en coordenadas polares si se usan
ángulos en radianes medidos de 0 a 2\pi?
a. u_\alpha=(\sqrt{2},\frac{7}{4} \pi)
b. u_\alpha=(2,\frac{1}{4} \pi)
c. u_\theta=(\sqrt{2},\frac{3}{4} \pi)
2. Se tiene un vector v=(-2,3), ¿Cuál es su representación en coordenadas polares si se usan
ángulos en grados medidos de 0^\circ a 360^\circ?
a. v_\alpha=(\sqrt{13},123.69^\circ)
b. v_\alpha=(13,303.69^\circ)
c. v_\alpha=(\sqrt{13},-123.69^\circ)
3. Utilizando las relaciones entre coordenadas polares y cartesianas, transforma la ecuación
y=x+1 a una ecuación polar de la forma R=f(\alpha) y elige la respuesta correcta.
a. R=\frac{1}{\sin \alpha-\cos\alpha}
b. R=\frac{1}{\sin \alpha +\cos\alpha}
c. R=-\frac{1}{\sin \alpha +\cos\alpha}
4. Transforme la ecuación polar R=\dfrac{1}{1-\cos\alpha} a una ecuación cartesiana y seleccione
la solución correcta de las opciones que se muestran.
a. y^{2}=2x+1
93
b. y=2x^2+1
c. y^{2}=-2x-1
5. Si se tiene un vector en coordenadas polares descrito por u_\alpha=(3 + 3 \sin \alpha, \alpha),
de las opciones siguientes ¿qué gráfica se obtendrá si variamos \alpha entre 0 y 2 \pi
radianes?
a.
b.
c.
6. Siguiendo el razonamiento presentado para la elipse selecciona ahora la ecuación correcta en
coordenadas polares que describe a la hipérbola que tiene los focos en F1=(0,0) y F2=(4,0) y
tiene sus vértices en (1,0) y (3,0).
a. \begin{displaymath} R=\frac{3}{1+2 \cos \alpha } \end{displaymath}
b. \begin{displaymath} R=\frac{2}{1-3 \cos \alpha } \end{displaymath}
c. \begin{displaymath} R=\frac{3}{1-2 \cos \alpha } \end{displaymath}
7. Aplicando los razonamientos anteriores ahora determina y selecciona la ecuación polar de una
parábola con foco en F=(0,0) y vértice en V=(2,0).
a. \begin{displaymath} R=\frac{4}{1+\cos \alpha}. \end{displaymath}
b. \begin{displaymath} R=\frac{4}{1-\cos \alpha}. \end{displaymath}
c. \begin{displaymath} R=\frac{1}{1+4\cos \alpha}. \end{displaymath}
8. Finalmente, calcula y elige la ecuación polar de la circunferencia centrada en el origen y de
radio igual a l.
a. R=l
b. R=l \cos \alpha
c. R=l \sin \alpha
9. Se sabe que la trayectoria del cometa Halley tiene una excentricidad de e= 0.967990 y su
afelio vale 35.1 UA (unidades astronómicas), ¿Cuánto vale el lado recto de su trayectoria?
a. Lado recto=2.2471 UA.
b. Lado recto=69.0764 UA
94
c. Lado recto= 1.12355 UA
10. Halla la excentricidad de la hipérbola que tiene como focos los puntos F1=(0, 0) y F2=(10, 0), y
6 como diferencia absoluta de las distancias a los focos.
a. excentricidad=\frac{5}{3}
b. excentricidad=\frac{10}{3}
c. excentricidad=\frac{6}{10}
11. ¿Cuál será la excentricidad de una elipse representada por la ecuación cartesiana:
\frac{x^2}{144}+\frac{y^2}{81}=1 ?
a. e=\frac{\sqrt{7}}{8}
b. e=\frac{12}{3\sqrt{7}}
c. e=\frac{3\sqrt{7}}{12}
12. Se tiene la ecuación cartesiana de una cónica: \frac{x^2}{9}-\frac{y^2}{4}=1. Selecciona una
ecuación polar de una cónica idéntica pero con un foco en el origen.
a. R=\frac{1.33}{1-1.2 \cos \alpha}
b. R=\frac{2.67}{1-0.36 \cos \alpha}
c. R=\frac{1.33}{1-2.67 \cos \alpha}
Ejercicios de Aplicación
1. El arco de un puente con una luz de 6m y una altura de 5m tiene una forma semielíptica. Un
camión de carga con una altura de 4m desea pasar por abajo. ¿Cuál es el ancho máximo
permitido para el camión?
a. 4.8 m
b. 3.6 m
c. 3.4 m
d. 4.9 m
2. Un jardinero quiere trazar una elipse que tenga de ancho 6m, ayudado con un lazo y dos
estacas. Las estacas las coloca en los focos separados entre sí 7m. ¿Cuál es la longitud del lazo?
a. 9.34 m
b. 13.36 m
c. 9.22 m
d. 9.64 m
3. La órbita del satélite Morelos alrededor de la Tierra tiene forma elíptica con respecto a ella en
uno de sus focos. Si la máxima y la mínima distancia del satélite a la Tierra es de 800 y 400
kilómetros, respectivamente, ¿Cuál es la excentricidad de la órbita?
a. 0.353
b. 0.234
c. 0.333
d. 0.345
4. El cable de suspensión de un puente colgante adquiere la forma de un arco de parábola. Los
pilares que lo soportan tienen una altura de 60m y están separados una distancia de 500m,
quedando el punto más bajo del cable a una altura de 10m sobre la calzada del puente.
95
5.
6.
7.
8.
9.
Tomando como eje x la horizontal que define el puente, y como eje y el de simetría de la
parábola, hallar la ecuación de esta. Calcular la altura de un punto situado a 80m del centro
del puente.
a. x^2-1250y+12500=0; 15.12m
b. x^2-125y+125=0; 15.12m
c. x^2-1250y+12500=0; 17m
d. x^2-125y+125=0; 17m
Se lanza una piedra horizontalmente desde la cima de una torre de 185m de altura con una
velocidad de 15m/s. Hallar la distancia del punto de caída al pie de la torre suponiendo que el
suelo es horizontal.
a. 92.5m
b. 95.2m
c. 90m
d. 98.5m
Un avión que vuela hacia el Sur a una altura de 1.500m y a una velocidad de 200km/h deja
caer una bomba. Calcular la distancia horizontal del punto de caída a la vertical del punto de
lanzamiento.
a. 972m
b. 927m
c. 729m
d. 792m
Un arco parabólico tiene una altura de 25m y una luz de 40m. Hallar la altura de los puntos del
arco situados 8m a ambos lados de su centro.
a. 21m
b. 12m
c. 25m
d. 18m
Un arco tiene forma de semielipse con una luz de 150m siendo su máxima altura de 45m.
Hallar la longitud de dos soportes verticales situados cada uno a igual distancia del extremo
del arco.
a. y=30\sqrt{2} metros.
b. y=1800 metros.
c. y=225\sqrt{8} metros.
d. y=25\sqrt{2} metros.
La tierra describe una trayectoria elíptica alrededor del Sol que se encuentra en un de los
focos. Sabiendo que el semieje mayor de la elipse vale 1485\times10^8km y que la
excentricidad es, aproximadamente, 1/62, hallar la máxima y la mínima distancias de la Tierra
al Sol.
a. Max: 1509\times10^8 km, Min: 1461\times10^8 km
b. Max: 1590\times10^8 km, Min: 1641\times10^8 km
c. Max: 2400\times10^8 km, Min: 1485\times10^8 km
d. Max: 1950\times10^8 km, Min: 1485\times10^8 km
96
10. Se lanza un proyectil desde un punto A con una velocidad inicial de 1000m/s formando un
ángulo de 35° con la horizontal. Hallar el alcance del proyectil y la duración de la trayectoria.
a. 95800m, 118s.
b. 9580m, 181s.
c. 9058m, 118s.
d. 98050m, 181s.
11. Hallar el ángulo con el que se debe lanzar un proyectil a una velocidad de 400m/s para que su
alcance sea de 12000m. Hallar, asimismo, la duración de la trayectoria.
a. 23° 42’; 32.8s.
b. 23° 24’; 23.8s.
c. 24° 43’; 38.2s.
d. 32° 24’; 32.8s.
12. Se lanza un proyectil con un ángulo de elevación de 60° y una velocidad inicial de 800m/s.
Hallar el alcance y el vértice de la trayectoria.
a. 56500m, 25000m.
b. 565m, 250m.
c. 55600m, 23000m.
d. 556m, 23m.
Tangentes a cónicas
1. Usando geogebra, o por inspección, obtenga una ecuación de la tangente a la grafica de 3x^{2}
+ 4y^{2} + 2x - 3y=0 en el origen. Elija la respuesta correcta entre las opciones que se dan.
a. 2x-3y=0
b. x-3y=0
c. x-y=0
2. Aplica la idea del problema anterior para obtener la ecuación de la recta que es tangente en el
punto S=(2,-1) a la elipse cuya ecuación es x^{2}+4y^{2}=8.
a. x-2y-4=0
b. x - 2y=0
c. 2 x - y=0
3. Se tiene una elipse descrita por la ecuación 4x^2+2y^2=1 y un punto R=(1,1) fuera de ella.
Existen dos rectas tangentes a la elipse que pasan por R. Calcula, usando geogebra las
coordenadas de los dos puntos donde cada tangente toca a la elipse y elige la respuesta
correcta.
a. los puntos son: (-0.1,0.69) y (0.43,-0.36)
b. los puntos son: (0.1,0.7) y (0.4,0.4)
c. los puntos son: (-0.1,0.7) y (0.4,-0.3)
4. Dos rectas que pasan por le punto R=(-3,4) son tangentes a la parábola cuya ecuación es
y^{2}=16x. Calcula y elige las ecuaciones correctas de estas rectas.
a. 2x-3y+18=0 y 2x+y+2=0
b. 3x-2y+18=0 y x+2y+2=0
97
5.
6.
7.
8.
9.
10.
c. 3x-2y-18=0 y x+2y-2=0
La ecuación de la tangente a la curva 4x^2+6y^2-24=0 en el punto A=(0,2) tiene la forma
y=mx+2. Si se resuelven simultáneamente ambas ecuaciones ¿cuál es el valor del
discriminante de las soluciones en x?
a. El discriminante es: 576m^2
b. El discriminante es: 576m^2-4(4+6m^2).
c. El discriminante es: 24m.
Obtener la ecuación de la tangente en el punto S=(3,4) a la hipérbola cuya ecuación es x^{2}\frac{y^{2}}{2}=1, y elegir entre las opciones la correcta.
a. 3x-2y-1=0
b. 3x-2y=0
c. 3y-2x-1=0
Usando geogebra determina la ecuación de la tangente a la cónica 3x^2 - 9x y - y^2 + x - y = 2
en el punto A=(-1,0) y selecciónala entre las opciones que se dan.
a. -5x+8y=5
b. -2x+4y=2
c. -2.5y+4x=2.5
Utilizando el método diferencial encuentra la pendiente m de la tangente a la ecuación 6x^22x+6y+12=0 en un punto arbitrario (x_0,y_0) sobre ella.
a. m=-\frac{6x_0-1}{3}
b. m=-\frac{3}{6x_0-2}
c. m=\frac{3}{12x_0-2}
Se tiene una cónica representada por la ecuación x^2 + x y + y^2 + 2x + 4y+1 =0. También se
sabe que el punto A=(0,-2+\sqrt{3}) está en la cónica. De entre las opciones siguientes escoge
la que contenga la información correcta.
a. La cónica es una elipse y la pendiente de su tangente en A vale: m=-\frac{1}{2}
b. La cónica es una elipse y la pendiente de su tangente en A vale: m=-0.5029
c. La cónica es una hipérbola y la pendiente de su tangente en A vale: m=2
Dos cónicas con ecuaciones y^2=4x+3 y \frac{x^2}{9}+\frac{y^2}{2}=1 se intersectan. El ángulo
de intersección entre ambas curvas se define como el ángulo que forman las dos rectas
tangentes a ellas en el punto de intersección. Usando GeoGebra encuentra el ángulo de
intersección entre ellas y selecciona la respuesta correcta.
a. 127.46^\circ
b. 197.46^\circ
c. 297.46^\circ
98