temas de química física ii - Universidad de Buenos Aires

2004
TEMAS DE QUÍMICA FÍSICA II
PARTE 3: DIFUSIÖN.
Parte 3a (versión 2.1)
1. Difusión. Generalidades.
2. La naturaleza física de la difusión.
3. Descripción fenomenológica de la difusión.
Parte 3b (versión 2.0)
4. Leyes de balance y continuidad. 2da. ley de Fick.
5. Integración de la 2da. ley de Fick.
Parte 3c (versión 1.3)
6. Difusión en sistemas electrolíticos.
7. No-acoplamiento entre migración eléctrica y difusión.
8. Intradifusión
Curso de Química Física II - 2do. cuatrimestre de 2004
Prof. Dr. Ernesto O. Timmermann
profesor titular regular DE
Departamento de Química
Facultad de Ingeniería
Universidad de Buenos Aires
2004
TEMAS DE QUÍMICA FÍSICA II
PARTE 3: DIFUSIÖN.
Parte 3a
(versión 2.1)
1. Difusión. Generalidades.
2. La naturaleza física de la difusión.
3. Descripción fenomenológica de la difusión.
Curso de Química Física II - 2do..cuatrimestre de 2004
Prof. Dr. Ernesto O. Timmermann
profesor titular regular DE
Departamento de Química
Facultad de Ingeniería
Universidad de Buenos Aires
Q FI I- 2M 4C 2 - F I - U BA ; D r.E.O .T im me rm an n
PARTE IIIa (versión 2.1)
1. Difusión. Generalidades
1.1. Introducción.
Se entiende por difusión a todo fenómeno espontáneo de transporte de masa, a temperatura y presión constantes, que se origina por inhomogeneidades espaciales en la
concentración y composición de un sistema. Este proceso irreversible tiende espontáneamente a homogeneizar la concentración y composición del sistema y el estado
homogéneo en concentración y composición a la temperatura y la presión dadas representa el estado …nal de todo proceso de difusión. Se observa que la difusión de
una sustancia siempre ocurre desde regiones donde su concentración es mayor a otras
donde su concentración es menor y que es tanto más rápida cuanto menor sea la
distancia sobre la cual se extiende la diferencia de concentración. En palabras más
concretas, el ‡ujo difusional siempre baja el gradiente de concentración y, en primera
instancia, es proporcional a éste. Esto queda expresado en lo que se conoce como la
ley empírica de Fick (1855), una de las más antiguas leyes de la Química Física, y
que se formula simplemente como una relación lineal del ‡ujo difusional (el efecto) y
el gradiente de concentración (la causa o ‘fuerza’ impulsora):
JK = ¡DK grad cK
(ley de Fick (1855))
(1.1)
Aun así, esta simple fórmula, donde J K es el ‡ujo de K, DK el coe…ciente de difusión
y grad cK el gradiente de la concentración cK , esconde una serie de interrogantes.
Qué es K, una sustancia, un componente, una especie, un ión, etc.? Cómo se mide
JK y respecto de qué sistema de referencia? Qué debe entiendese por DK ?
A continuación trataremos de responder y aclarar estas cuestiones.
1.2. Sistema de referencia de volumen …jo y convección.
1.2.1. Difusión y convección.
El transporte por difusión es un fenómeno típico de mezclas o soluciones. El sistema
más simple en el cual se lo observa es, entonces, binario. El observador …ja su atención,
en general, en uno de los dos componentes de esta mezcla o solución binaria, en aquel
por el cual tiene especial interés, cualquiera que éste sea. Sigue su ‡ujo desde la (región
de) concentración mayor hacia la concentración menor y opera en consecuencia. Sin
embargo, si hay un gradiente de concentración de uno de los dos componentes tiene
que haber también un gradiente en sentido contrario para el otro componente, pues
si en una región la concentración de uno de ellos es mayor la del otro es menor y
si en otra su concentración es menor allí la del otro será mayor. Y, por lo tanto,
tiene que haber también un proceso difusional para ese otro componente y su ‡ujo
será forzosamente en sentido contrario al ‡ujo del primer componente ya que sus
gradientes de concentración son contrarios.
De aqui se concluye que el proceso difusional es, en realidad, compuesto e involucra al menos los ‡ujos o transporte de dos sustancias simultáneamente. Es, entonces,
un proceso en el cual se observa el desplazamiento espontáneo relativo entre sí de, al
menos, dos sustancias. Y esto es siempre un proceso local, que ocurre ya en un punto
dado y dentro de un elemento de volumen del sistema, siempre y cuando exista allí la
necesaria inhomogeneidad de concentraciones, es decir, los correspondientes gradiente
de concentración. Y ello ocurre independientemente de cualquier otra condición del
sistema, al cual consideraremos por ahora como isotérmico e isobárico. Una condición adicional puede ser que ese elemento de volumen, dentro del cual tiene lugar
ese proceso (mutuo) de difusión, se desplace a su vez en el espacio como un todo.
Ese movimiento es, en general, observable desde afuera del sistema y se denomina
convección. Respecto de cada sustancia ambos procesos se superponen y la velocidad
total es la suma vectorial de ambas contribuciones. Por lo tanto, es natural referir la
velocidad o el ‡ujo difusional de una sustancia a la velocidad convectiva común de
todos los componentes del elemento de volumen en cuestión.
En general la convección se produce por causas externas, p.ej. por diferencias de
presión y/o por agitación, y entonces se la denomina convección forzada, o a consecuencia de los procesos de transporte propiamente dichos que ocurren dentro sistema,
que causan, por ej., diferencias espaciales de densidad, y entonces se la denomina
convección libre o natural.
Convección puede ocurrir ya en sistemas monocomponente o puros. Por convección
la cantidad de sustancia transportada a través de un plano solidario con la celda en
el tiempo dt y por el área dq es c £ v cvx £ dt £ dq , donde c es la concentración molar
de la sustancia y v cvx la velocidad convectiva relativa a la celda y común a todas las
partículas transportadas y contenidas en el volumen transferido. El volumen asociado
es evidentemente V¹ £ c £ v cvx £ dt £ dq , donde V¹ (= 1=c) es el volumen molar de
la sustancia en cuestión. Entonces la densidad de ‡ujo de volumen c JV relativo a la
celda, es decir, la cantidad de volumen transferida por unidad de tiempo y unidad de
área, es directamente
(1.2)
c JV = v cvx
o sea, (la densidad de) el ‡ujo de volumen c JV está directamente dado por la velocidad
de convección vcvx . O, en otras palabras, la aparición de un ‡ujo de volumen es la
característica del fenómeno de transporte de materia por convección.
Este concepto se puede extender fácilmente a sistemas multicomponentes. El ‡ujo
de volumen c JV tendrá entonces una contribución de cada componente K igual a
V K cK v K , siendo VK su volumen parcial molar, cK su concentración y su velocidad
v K : Queda
X
(cK VK )vK = w
(1.3)
c JV =
K
donde w es la velocidad media del elemento de volumen de…nida ya en secciones
anteriores.
Si el único proceso de transporte es el convectivo las velocidades de todos los
componentes serán iguales a la velocidad convectiva [8 vK = v cvx ] y queda
X
X
(cK VK )vK =[
cK VK ] vcvx = v cvx
(1.4)
c JV =
K
|
K
{z
=1
}
Por lo tanto, se puede identi…car la velocidad de convección vcvx con la velocidad media
w del elemento de volumen.
vcvx = w
(velocidad de convección)
2
(1.5)
Y, por el contrario, la ausencia de movimiento de volumen (w = 0) indicará la ausencia
de movimiento convectivo.
En consecuencia, la velocidad vK de cada componente K respecto de la celda se
puede desdoblar en una contribución relativa a la velocidad media de volumen y otra
debida a la convección:
vK
=
(v K ¡ w)
vel:relativa a la celda ve l:relativa de volu men f ijo
+
w
vel:convectiva
(1.6)
y multiplicando por cK se obtienen las respectivas contribuciones al ‡ujo ’absoluto’
c JK (relativo a la celda) del componente K, esto es:
cJ K
= cK vK = cK (v K ¡ w) + cK w =
|{z}
f lujo relativo a la calda
w JK
+
|{z}
f lujo dif usivo
cvx JK
| {z }
f lu jo convectivo
(1.7)
O sea, el ‡ujo c J K está constituído por dos contribuciones, una difusiva y otra
convectiva. Y, de acuerdo con todo lo dicho más arriba, hemos identi…cado como
el ‡ujo difusivo a la parte del ‡ujo de K relativa a la velocidad media del elemento de
volumen, a saber
‡ujo difusivo
(1.8)
w JK ´ c K (v K ¡ w)
w JK
describe así el movimiento relativo de los componentes entre si dentro del elemento de volumen, independientemente si este elemento se mueve o no. Consecuentemente se denomina al SR de volumen …jo como el sistema de referencia de Fick o
sistema de referencia de difusión. Y el ‡ujo en la ley de Fick debe medirse lógicamente respecto de este SR si se quiere caracterizar adecuadamente al fenómeno de
difusión.
1.2.2. Flujos y fuerzas empíricas para difusión.
Tanto las fuerzas como los ‡ujos en difusión se plantean siempre para las sustancias
que migran en forma independiente (SMI), aunque este concepto no se aclare siempre
en los textos y que se analizará en la sección siguiente. Como ya se ha visto el SR de
difusión es la velocidad media w del elemento de volumen y al ser éste un SR interno
no todos los ‡ujos son independientes. Tenemos:
X
w=
cK V K v K ) w JK = cK (v K ¡ w) y ! K = cK V K
(1.9)
K
X !K
cK
wJ K
=0
K
)
P
K
(1.10)
VK w J K = 0
Por su parte, las fuerzas empíricas de la difusión, o sea, los gradientes de concentración. tampoco son todas independientes. Teniendo en cuenta la de…nición de
volumen de mezcla y la relación de ec. de Gibbs-Duhem para los volúmenes parciales
molares tenemos:
X
X
X
X
V =
nJ VJ ) 1 =
cJ VJ ) 0 =
cJ dVJ +
V J dcJ
(1.11)
J
J
como por G.D.
J
X
cJ dV J = 0
J
3
)
J
X
J
V J dcJ = 0
P
)
J
(1.12)
V J gradcJ = 0
Entonces, para los ‡ujos y fuerzas empíricas de difusión valen las siguientes condiciones generales de clausura a T y P constantes:
P
J
VJ
w JJ
=0
y
P
J
V J gradcJ = 0
(T y P ctes.)
(1.13)
1.2.3. Sustancias que migran independientement (SMI).
La segunda pregunta a contestar es cuales son las ’sustancias’ que migran por difusión
y a las cuales se debe aplicar la ley de Fick y las condiciones dadas por (1.13). En
otras palabras, se trata de determinar las ’sustancias que migran independientemente’
(SMI) y éstas no tienen porqué coincidir con especies o componentes del sistema en
el sentido de la regla de las fases (RdlF). Algunos ejemplos de sistemas binarios (en
el sentido de la RdlF), algunos conteniendo más de dos especies, permitirán …jar
conceptos.
(a) Metanol-benceno. Sea una mezcla líquida de dos sustancias que son líquidas
en estado puro, p.ej. la mezcla de metanol-benceno. Si en esta mezcla hay inhomogeneidades de composición es obvio que ambas sustancias difunden en sentido
contrario en forma espontánea para reducirlas. En este caso no hay dudas y las SMI
son dos y los conceptos de SMI para especies y para componentes según la RdlF son
coincidentes. Estas consideraciones también valen si la mezcla fuese gaseosa (mezcla
de vapores).
(b) Glucosa-agua. En una inhomogénea solución acuosa de glucosa se dirá que
difunde glucosa desde su concentración mayor a su concentración menor y debe aceptarse que el solvente agua difunde simultáneamente en sentido contrario. Las conclusiones son entonces las mismas que en el caso anterior; las SMI son dos y no hay
problema de indenti…carlas como sustancias, especies o componentes de la RdlF.
(c) Cloroformo-dióxido de nitrógeno. Sea ahora la mezcla inhomogénea (gaseosa
o líquida) de cloroformo-dióxido de nitrógeno. Es conocido que aqui existe la asociación a tetróxido de nitrógeno según 2 N2 O ¿ N4 O 2. Tenemos entonces un sistema
binario (RdlF) inhomogéneo con tres especies y solo una concentración independiente, p.ej. la fracción molar de cloroformo. Es evidente que, por un lado, difundirá
cloroformo, pero qué especie o especies difunden en sentido contrario?. Difundirán
tanto N2 O como N4 O 2 , pero lo harán en forma independiente? Consideremos que
se veri…ca que el proceso de asociación está en equilibrio en todo punto espacial y
en todo momento (equilibrio químico local) aunque el sistema sea inhomogéneo. Entonces, si el monómero difunde más rápido que el dímero, se producirá localmente un
exceso de monómero y habrá asociación para recuperar el equilibrio, y si el dímero es
más rápido habrá localmente un exceso de éste y se producirá disociación del mismo
para mantener el equilibrio. El resultado es que la velocidad del componente presenta
una velocidad promedio en número de ambas especies. Entonces para la difusión hay
solo dos SMI, el cloroformo y N2 O ó N4 O2 , para este sistema binario de tres especies
moleculares.
Debe entenderse bien que este resultado es consecuencia directa de la suposición
del equilibrio químico local. Esta suposición demanda que las reacciones de asociación
4
y de disociación sean mucho más rápidas que el proceso de difusión y, por lo tanto, el
equilibrio se recupera instantáneamente de cualquier apartamiento ocasionado por la
difusión de las moléculas involucradas. Por su parte, si la suposición no es aplicable
y tanto las velocidades del proceso químico como del difusional son del mismo orden
de magnitud debe aceptarse que son tres las SMI, y deben tenerse en cuenta estos
hechos en las ecuaciones de balance del tipo que deban plantearse, incluyendo términos
correspondientes a la reacción de asociación. En conclusión la suposición del equilibrio
local simpli…ca mucho, como se verá, los planteos para describir el proceso difusional.
(d) Solución acuosa de un electrólito simétrico. Sea ahora una solución acuosa de un electrólito simétrico. Es un sistema binario de dos componentes (RdlF) y/o
de un componente molecular (agua) y dos constituyentes iónicos, y de cuatro especies,
si se considera al electrolito como parcialmente disociado (solvente, catión, anión y
molécula sin disociar). Y hay una sola variable de concentración independiente, la
molalidad m del electrólito. Es evidente que el agua difunde ba jando su propio gradiente de concentración, es decir, en contra del gradiente del electrólito, pero qué especie
difunde según este gradiente, el electrólito como tal (y cómo debe entenderse esta denominación), los constituyentes iónicos o las especies iónicas y la molécula sin disociar?
Es evidente también que el observador presta más atención al comportamiento del soluto electrolítico que al del solvente y debemos dar una respuesta no-ambigua. Hay
dos condiciones adicionales a considerar: a) experimentalmente se observa que por difusión pura de un ’componente’ electrolítico no circula corriente eléctrica, aunque es
evidente que hay movimiento de los portadores de cargas eléctricas, y b) el equilibrio
químico local para el proceso de diso ciación del electrólito. La primera condición vale
tanto a nivel de constituyente iónico y de especies, y, de acuerdo con lo visto en el
capítulo de conducción eléctrica, podemos escribir:
I = 0 =zc cc vc + za ca va =z+ c+ v+ + z¡ c¡ v¡
|
{z
} |
{z
}
c on st . ió nic os
(1.14)
esp ec ie s ión ica s
Teniendo en cuenta la condición de electroneutralidad a ambos niveles (zc cc = ¡z a ca ;
z +c+ = ¡z¡ c¡ ) la conclusión es directa: las velocidades difusionales de los dos portadores de carga involucrados a cada nivel son iguales, esto es,
v dif
= vadif ;
c
dif
dif
v+ = v¡
(difusión)
(1.15)
Por esto hay una sola velocidad difusional independiente, que a nivel de constituyente iónico la tomamos como v2 , la velocidad difusional del electrólito, o sea, del
componente 2 del sistema. A nivel de especies tenemos que considerar también la
condición de equilibrio local. Si los iones son más veloces que la ’molécula’ sin disociar habrá un proceso de asociación y si, por el contrario, esta ’molécula’ es más
veloz que los iones habrá espontáneamente un proceso de disociación, siempre para
mantener en equilibrio (local) a este proceso. Por lo tanto, tenemos, por un lado, la
velocidad vn de la ’molécula’ n sin disociar y, por otro, las velocidades difusionales de
los dos iones, que deben ser iguales ya que, por lo ya dicho, no se transporta carga
eléctrica por difusión. Estas últimas las tomamos como v e ; la velocidad difusional de
la ´parte´ iónica (electrolítica) del componente 2. Entonces a nivel de especies también hay una sola velocidad independiente v 2 , que será ahora un promedio en número
entre v n y ve : Por lo tanto, queda
v2 ´ vcdif = v dif
;
a
dif
v n ; ve ´ v+
= vdif
¡ ;
5
v2 = f (ve ; v n ) (difusión)
(1.16)
Debemos concluir también en este caso que hay solamente dos sustancias que migran
en forma independiente (SMI) por difusión.
En general concluímos también que tanto la condición de ’no transporte de carga
por difusión’ como cada condición de equilibrio químico local disminuyen, cada una
en uno, el número de sustancias que migran independientemente.
(e) Ácido sulfúrico-agua. Consideremos ahora la solución de un electrólito nosimétrico, p.ej. el caso ya analizado del ácido sulfúrico en el capítulo de conducción
eléctrica. El sistema es binario, de dos constituyentes iónicos y de cinco especies
2¡
+
iónicas y moleculares (H2 O, H2 SO 4 , HSO¡
4 , SO 4 , H ). Por las tres condiciones,
la de no-circulación de corriente eĺéctrica, y los dos equilibrios de disociación, que
suponemos rápidos, de este ácido, hay también aquí solo dos SMI, una es el solvente
y la otra el electrólito estequiométricamente considerado.
(f ) KHSO4 -agua. Sea ahora la solución acuosa de un electrólito ternario, p.ej.
KHSO4 . Hay dos componentes (RdlF), tres constituyentes iónicos y siete especies
2¡
+
+
(H2 O, KHSO 4 , H2 SO4 , HSO ¡
4 , SO4 , H , K ). Tenemos nuevamente las tres condiciones de contorno del caso (e) y una condición de electroneutralidad, y, por lo tanto,
hay aquí tres sustancias que migran en forma independiente por difusión (como H2 O,
K 2 SO4 y H2 SO 4 ). Por difusión no se lesiona la condición de electroneutralidad, pero
otras condiciones sí. Asi para el equilibrio (la solución homogénea), es decir, en ausencia de gradientes de concentración, vale las condiciones cK = cH = cSO4 , a nivel de
constituyentes iónicos, por la preparación del sistema (se agrega KHSO 4 ) y hay una
sola variable de concentración. Fuera del equilibrio, por difusión, estas condiciones se
rompen y se reducen a una sola, a saber cK +cH = 2 cSO4, y entonces se debe describir
el proceso difusional considerando el movimiento difusional de tres sustancias.
En conclusión, en este caso la cantidad de variables que describen el estado de
equilibrio y la de las que describen el estado de no-equilibrio no coinciden y esto debe
tenerse como una característica importante del fenómeno difusional. Siempre debe
establecerse correctamente la cantidad de SMI a considerar. No todo sistema binario
tiene solo dos SMI, pero toda solución de un electrolito de dos constituyentes iónicos
es de esta clase. En cambio, el caso tratado del sulfato ácido de potasio se comporta,
desde el punto de vista difusional, como la solución mezcla de NaCl-KCl. Ambos son,
difusionalmente hablando, ternarios, aunque el primero es binario desde el punto de
la RdlF y el segundo no, ya es que ternario también para esta regla.
Entonces, como conclusión …nal, debe decirse que la ley de Fick debe aplicarse
siempre para SMI.
1.3. Difusión en un sistema binario.
Para la difusión en un sistema binario (dos SMI) vale según (1.13):
V1
w J1
+ V2
wJ 2
=0
y
V1 grad c1 + V 2 grad c2 = 0
(1.17)
y se tiene solo un ‡ujo y un gradiente independientes. Ya que la elección de qué componente se toma como independiente es completamente arbitraria, se puede escribir
6
Datos de coeficientes de difusión
Gases
Líquidos
Polímeros
Sólidos
D = 1,0 cm 2/s
1,28 cm2/s H2(g) 1 atm 273 K
0,70 cm2/s O 2(g)-H2 (g) 1 atm 273 K
D = 0,1 cm 2/s
0,18 cm2 /s O 2(g) 1 atm 273 K
0,20 cm2/s O 2(g)-N2(g) 1 atm 285 K
0,18 cm2/s N2(g) 1 atm 273 K
0,088 cm2/s tolueno-aire 1 atm 293 K
D = 1,0.10-5 cm 2/s
0,8.10-5 cm 2/s H20-EtOH(x=0,1) 298 K
1,2.10-5 cm 2/s H20-MgClý(m=0,001) 298 K
6.10-5 cm 2/s H20-NaCl(m=0,001) 298 K
3,2.10-5 cm 2/s Bz-n-hept.(x=0.5) 298 K
2,3.10-5 cm 2/s H20 298 K
2,2.10-5 cm 2/s Benceno 298 K
1,9.10-5 cm 2/s D20 298 K
D = 1,0.10-6 cm 2/s
4,7.10-6 cm 2/s H20-sacarosa 298 K
6,0.10-6 cm 2/s H20-MgSO4(m=0,2) 298 K
7,9.10-6 cm 2/s Na-Hg 283 K
D = 1,0.10-7 cm 2/s
6,1.10-7 cm 2/s H20-seroalbúmina 298 K
D = 1,0.10-6 cm 2/s
1,3.10-6 cm 2/s H20 en PVA 298K
1,8.10-6 cm 2/s H2 en p-butadieno 293 K
2,0.10-6 cm 2/s Tol.en p-estireno 298 K
D = 1,0.10-7 cm 2/s
2,4.10-7 cm 2/s N2 en p-butadieno 293K
D = 1,0.10-8 cm 2/s
1,3.10-8 cm 2/s Acetona en Ac-Celul. 293K
D = 1,0.10-10 cm 2/s
0,9.10-10 cm 2/s Bz en PVAc 313 K
3,5.10-10 cm 2/s H2 en SiO 2 473 K
D = 1,0.10-13 cm 2/s
4,6.10-13 cm 2/s H2 en Pyrex 293 K
D = 1,0. 10-5 cm 2/s
1,7.10-5 cm 2/s Cu en AgI 500 K
D = 1,0. 10-7 cm 2/s
2,4.10-7 cm 2/s Cu en AgCl 511 K
D = 1,0. 10-10 cm 2/s
2,1.10-10 cm 2/s Na en AgCl 300°C
3,2.10-10 cm 2/s Au en Ag 770°C
6,8.10-10 cm 2/s Cr en Fe 1150°C
D = 1,0. 10-11 cm 2/s
5,8.10-11 cm 2/s Zn en Cu 350°C
D = 1,0. 10-13 cm 2/s
1,5.10-13 cm 2/s Cu en Au 300°C
D = 1,0. 10-16 cm 2/s
4,9.10-16 cm 2/s Pb en PbI2 410 K
la ecuación de la ley de Fick tanto para uno como para el otro componente:
wJ 1
= ¡D1 grad c1
y
w J2
= ¡D2 grad c2 ;
(1.18)
Ambas relaciones se vinculan simplemente según
V1
w J1
= ¡V 2
= V 1 (¡D1 grad c1 ) = D1 (¡V 1 grad c1 ) =
w J2
= ¡V 2 (¡D2 grad c2 ) = ¡D2 (¡V 2 grad c2 )
(1.19)
Se concluye que los dos coe…cientes D1 y D2 son idénticos y se de…ne un solo coe…ciente
de difusión según
D1 = D2 ´ D > 0:
(1.20)
Entonces, para un sistema binario, existe un solo coe…ciente de difusión mutua o
de interdifusión D, que no puede adjudicarse a un componente en particular, sino
que corresponde al sistema. Correspondientemente, la ley de Fick debe formularse en
las siguientes formas equivalentes, ya que ambos componentes se mueven en el proceso
difusional,:
o¶
(1.21)
w J2 = ¡D grad c 2
w J 1 = ¡D grad c 1 ;
usándose usualmente la del componente minoritario (soluto), muchas veces de solubilidad limitada, para el cual eligimos el índice 2.
Las dimensiones de D son las siguientes:
fDg =
ff lujog
mol cm ¡2 s¡1
=
= cm2 =s (usual) o¶ m 2 =s (SI)
fgrad cg
[mol cm ¡3 ]=cm
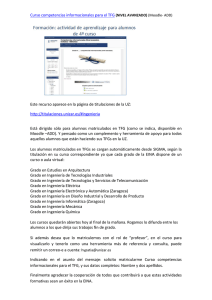
Valores típicos son:
gases: D » 0:1 ¡ 1 cm 2 =s (marcada dependencia con P y T)
líquidos: D » 1 £ 10 ¡5 ¡ 10 ¡6 cm2 =s (dependencia con T y P(en menor grado)
sólidos: D » 1 £ 10¡ 7 ¡ 10 ¡19 (¤ ) cm2 =s (dependencia con T y P(en menor
grado) [ ¤ ) : tomado como mínimo valor medible].
En la tabla adjunta se dan ejemplos para sistemas de distinta naturaleza …sicoquímica.
Para ver qué signi…can estos valores se puede calcular la velocidad con que se
mueven las partículas por difusión. Sea una concentración unitaria (c2 =1 mol/dm3 )
y una diferencia de concentración unitaria (¢c2 =1 mol/dm3 ) que se extiende sobre
una distancia unitaria (¢x=1dm), esto es, un gradiente de gradc2 = ¢c2 =¢x= 1 £
3
3
(mol/dm
)/dm= 0.1£(mol/dm
)/cm: Entonces tenemos: (v 2 ¡w)= jD £ (grad c2 )=c2 j
¯
¯
2
¡ 1¯
¯
= D(cm =s) £ 0:1 cm = j0:1 £ Dj cm/s. Usando los valores arriba indicados resulta que para gases la velo cidad es de 0.1 cm/s y para líquidos de 10 ¡6 cm/s. Estas
velocidades son mucho menores que la velocidad media de agitación térmica y no
’perturban’ el equilibrio de distribución de velocidades.
Por estos ba jos valores los procesos difusionales, al igual que las migraciones generadas por un campo eléctrico (ver capítulo de conducción eléctrica), son movimientos furtivos (sigilosos o reptantes) (creeping motions) ya que, en general, no son observables a simple vista. A diferencia del movimiento direccionado en un campo eléctrico el movimiento difusional es caótico, es decir, al azar (movimiento browniano)
en cualquier dirección. Tiene, sin embargo, un resultado neto de ‡ujo ya que, en
promedio temporal, más partículas se trans…eren de la región de mayor concentración
a la de menor concentración que en sentido inverso. (Ver capítulo siguiente).
8
El coe…ciente D es siempre positivo y depende en general de la concentración (c2 ) o
composición (x2 ) del sistema, de la temperatura y de la presión (en menor grado).
A grandes diluciones D es en general constante y presenta el siguiente límite para
c2 ! 0 :
1(1)
D(c2 ) ) lim D = D2
(1.22)
c2 !0
donde el supraíndice (1) indica el medio en el cual difunde el soluto 2.
Para sistemas binarios de componentes miscibles en todas las proporciones (0 ·
x 2 · 1) este límite se encuentra en ambos extremos del rango de composición:
1(1)
lim D = D2
x2 !0
1(2)
( D(x 2 ) ) lim D = D1
x 2!1
(1.23)
Los valores límites se adjudican a los componentes en situación de dilución in…nita
(situación de vestigio), adjudicación que es físicamente lógica y que tiene también
fundamento teórico (ver, más adelante, la interpretación del coe…ciente de difusión).
Para ilustrar estos efectos en las láminas adjuntas se presentan ejemplos de la
dependencia con la concentración del coe…cientes de inter -difusión para distintos sistemas …sicoquímicos.
La primera presenta los datos para dos mezclas de solventes, benceno-ciclohexano
(R.Mills J.Phys.Chem. 69(1965)3116) y benceno n-heptano (K.R.Harris, C.K.Pua y
P.J.Dunlop J.Phys.Chem. 74(1970)3518). Las …guras son las originales de los trabajos citados e incluyen tanto los datos de inter difusión como los de intra difusión
(difusión de moléculas marcadas) para ambos componentes en función de la composición (fracción molar) de las mezclas. Obsérvese que para la interdifusión se cumplen
los límites señalados por (1.23). La característica de la intradifusión y sus diferencias
con la interdifusión se explicarán en un capítulo posterior (Parte 3c).
En la segunda lámina se presentan datos de difusión de soluciones. La primera
…gura corresponde a soluciones acuosas de solutos moleculares (no-electrolitos): urea,
tiourea, ¯-alanina, mannitol y sucrosa. La …gura (7.19) corresponde al libro “Di¤usion
in liquids. A theoretical and experimental study.” por H.J.V.Tyrrell y K.R.Harris,
Butterworths, 1984. En esta …gura también se presentan datos de interdifusión (símbolos llenos) y de intradifusión (símbolos vacios) en función de la molaridad c2 del
soluto. Salvo para el caso de tiourea los valores de intradifusión son siempre menores
a los de interdifusión. Obsérvese que se cumple el límite indicado por (1.22).
La segunda …gura corresponde a soluciones acuosas de electrolitos de distintas
valencias. Se representa el valor del coe…ciente de interdifusión relativo a su valor de
dilución in…nita (D± ) en función de la raíz cuadrada de la molaridad c2 de las sales.
La …gura (12) corresponde al libro “Thermodynamics of Irreversible Processes.” por
R.Haase, Addison-Wesley, 1969 (las ecs.(40) y (43) que se citan en la leyenda se
discuten en el capítulo de difusión de electrolitos de la presente serie de textos (Parte
p
3c)). Obsérvese tanto la ley lineal en c2 a grandes diluciones como el efecto de las
cargas eléctricas de los iones, ambos características generales de las propiedades de
soluciones electrolítcas.
Finalmente en la tercera lámina se presentan dos casos especiales para interdifusión. La primera …gura ilustra la interdifusión en soluciones de polímeros; la …gura
(2.9) corresponde al libro “Di¤usion. Mass transfer in ‡uid systems.” por E.L.Cussler,
Cambridge Univ. Press, 2da. edición 1997. Se presentan datos tanto en la región
10
diluída (soluciones ‡uídas de macromoléculas) como en la regíon muy concentrada
(comportamiento típico de membranas) en función de la fracción en peso del polímero.
Obsérvese la marcada dependencia con la concentración en ambos casos. Los sistemas
diluídos corresponden a poliestireno en tolueno y en ciclohexano, respectivamente, y
los sistemas ‘membrana’ tratan de benceno en goma natural, metilacetato en polimetilacetato y cloruro de alilo en poliacetato de vinilo (repárese en la forma de describir
los sistemas, nombrándose el componente minoritario en primera instancia).
La segunda …gura presenta interdifusión en cercanías de un punto crítico en función
de la temperatura. El sistema es la mezla equimolar de n-hexano-nitrobenceno, que
presenta un punto crítico superior de miscibilidad a 19.9§0.1 ± C: Al disminuir la
temperatura a composición constante el coe…ciente de interdifusión se anula en el
punto crítico. Este efecto se debe al comportamiento del factor termodinámico de la
difusión (ver capítulo subsiguiente) en puntos críticos. La …gura (11) corresponde al
libro de Haase citado más arriba.
1.4. Difusión en sistemas multicomponentes.
Por (1.13), esto es,
X
VJ
w JJ
=0
X
y
J
V J grad cJ = 0
J
si hay Q componentes (SMI) solo Q-1 ‡ujos independientes y Q-1 gradientes de concentración son independientes. Para estos la experiencia indica la siguiente generalización
de la ley de Fick:
P
(‡ujos y gradientes independientes)
(1.24)
wJ J = ¡
K DJ K grad c K
es decir, los ‡ujos difusionales independientes dependen de todos los gradientes de
concentración independientes, generalización que es con…rmada por la teoría (ver más
adelante). Hay, por lo tanto, dos tipos de coe…cientes de difusión: los directos, principales o diagonales DJ J , que describen la dependencia del ‡ujo de un componente de su
propio gradiente de concentración, y los cruzados, de interacción o de acoplamiento
D JK , que describen la in‡uencia de los gradientes de otros componentes sobre el
‡ujo de un componente dado. Los coe…cientes principales DJ J son siempre positivos,
mientras que los de acoplamiento pueden presentar cualquier signo. Para estos últimos
no vale una ley de simetría, pero la teoría termodinámico-fenomenológica (mediante
las relaciones de reciprocidad de Onsager) demuestra que están relacionados entre sí
y solo la mitad son independientes.
Así para un sistema ternario las ecuaciones de ‡ujos difusionales son:
wJ 2
=
D22 grad c2 + D23 grad c3
wJ 3
=
D32 grad c2 + D33 grad c3
(1.25)
donde se ha tomado al componente 1 (arbitrariamente) como el componente dependiente. Aqui
D22 ; D33 > 0; D23 6= D32
(1.26)
La descripción general de interdifusión en sistemas multicomponentes se desarrolla
en el curso de FISICOQUÍMICA ESPECIAL.
____________________
13
Q FI I- 2M 4C 2 - F I - U BA ; D r.E.O .T im me rm an n
2. La naturaleza física de la difusión.
2.1. Difusión y movimiento browniano.
El fenómeno de difusión es un fenómeno escalar. Pues, aunque la ley de Fick (1.21) (y
también (1.24)) incluye ‡ujos y gradientes de concentración que son magnitudes con
propiedades direccionales, es decir, con caracteñisticas vectoriales, no existe ninguna
fuerza efectiva real cuyo efecto resultante sea un ‡ujo neto de materia en cierta dirección. Una molécula no ‘siente’ o ‘sabe’ que está ubicada dentro de una inhomogeneidad espacial de concentración, es decir, que está unbicada dentro de un gradiente
de concentración. Por lo tanto surge inmediatamente la pregunta acerca de la real
naturaleza física de este fenómeno de transporte. La explicación la dieron Maxwell y
Boltzmann mediante la Teoría Cinético-Molecular de la materia y, en particular, de
los gases, cuyo postulado básico es la existencia de la agitación (movimiento) térmica
de las moléculas.
La existencia de la agitación o movilidad térmica de las moleculas es ampliamente
con…rmada por la experiencia y por todo lo que enseña la física y la química clásicas.
Así es la agitación térmica la que origina la ‘fuerza impulsora’ que lleva un gas a ocupar
espontáneamente todo el volumen del recipiente que lo contiene y ella también es la
que origina la tendencia espontánea de igualar la concentración en todo el volumen
de cualquier sistema monofásico, o sea, la agitación térmica es la que ‘impulsa’ todo
aquello que macroscópicamente se manis…esta por lo que se denomina genericamente
como difusión.
a). Movimiento al azar y movimiento browniano. Considerando el comportamiento de una sola partícula, el movimiento térmico le da una velocidad media
que decrece al aumentar la masa (m) de la partícula, de tal forma que, a temperatura
dada (T) y en ausencia de campos externos, la energía cinética es la misma para todas las partículas. La velocidad media (u) en cierta dirección está dada por mu2 =kT,
donde k (=R/NAv ) es la constante de Boltzmann, R la constante de los gases y NAv
la constante de Avogadro. Por otra parte, aún teniendo esta velocidad media toda
partícula individual debe cambiar frecuentemente de dirección y de velocidad debido
a las colisiones con otras partículas y con las paredes del recipiente. Por lo tanto, cada
partícula sigue en realidad un derrotero en zig-zag muy complicado e irregular, muy
difícil de describir, cuya naturaleza está determinado exclusivamente por estas colisiones al azar. Si las partículas son lo su…cientemente grandes para ser distinguibles
su movimiento se denomina movimiento browniano, en memoria del botánico Brown
que lo describió por primera vez.
Estas dos manisfestaciones de la agitación térmica, difusión a nivel macroscópico
y movimiento browniano a nivel de partículas, están ambas íntimamente relacionadas
y dependen ambas de las características de las partículas. Veamos estas relaciones.
Como ya se ha dicho, el real movimiento de una partícula es el resultado puramente mecánico de las innumerables colisiones entre todas las partículas del sistema.
Cada colisión determina un cambio en la dirección del movimiento y un cambio en la
velocidad y hay billones de colisiones por segundo (véase detalles de la Teoría Cinética
de los Gases). Obviamente un movimiento cambiando tan rápidamente no se puede
seguir en detalle. Sin embargo se puede observar mediante un microscopio la posición
de ciertas partículas ‘distinguibles’ a intervalos de tiempo razonablemente espaciados.
14
Si estas posiciones se unen mediante lineas rectas se obtiene una representación de un
zig-zag completamente irregular, como debe esperarse dado el carácter al completo
azar de las colisiones moleculares.
En la lámina adjunta la …gura superior presenta en su parte (a) un tal zig-zag
del movimiento browniano en un plano experimentalmente obtenido mediante observaciones con microscopio por Perrin (1923) observando el movimiento de partículas
de gutagamba (pigmento gomoso natural amarillo). Si se conecta, por ejemplo, cada
décima posición observada se obtiene un zig-zag mucho más suave, tal como lo muestra la parte (b). Por otra parte, si las observaciones se hubieran hecho en intervalos de
tiempo diez veces menores, cada segmento del zig-zag original en (a) sería reemplazado
a su vez por un zig-zag de diez miembros, y el aspecto de la …gura sería aún mucho
más irregular. Por lo tanto, cualquiera de estas …guras representa la trayectoria de
una partícula solo mediante una gran sobresimpli…cación de su derrotero real.
Una suposición simple para describir estos movimientos es aceptar que la dirección
y la longitud de cada segmento del zig-zag es completamente independiente de las
del paso previo. Las direcciones son completamente al azar y las longitudes varían
irregularmente alrededor de un valor medio. Este tipo de movimiento se denomina
‘vuelo al azar’. Si se supone además que la longitud de los distintos segmentos es
siempre igual al valor medio el planteo se simplica más y se habla de un ‘camino al
azar’ de pasos iguales con direcciones al azar.
Si se restringe el movimiento a un plano se tiene un camino al azar bi-dimensional,
y si se lo restringe a un eje será uni-dimensional. En este último caso el movimiento
tendrá solo dos posibilidades direccionales, hacia la izquierda o derecha o hacia arriba o
aba jo, o una positiva y otra negativa, para cada paso. Para el caso bi-dimensional estas
posibilidades para cada paso ya son cuatro y seis para el camino tri-dimensional y las
trayectorias serán tanto más complejas cuantas más grados de libertad (dimensiones)
sean accesibles a la partícula. Asi la …gura de Perrin se puede considerar como la
proyección en un plano de la trayectoria tri-dimensional. A su vez, la proyección de
esta …gura sobre un eje resultará en una trayectoria al azar uni-dimensional mucho
más simple, como se puede observar a simple vista, ya que pesan solo pasos hacia
arriba y abajo o hacia derecha e izquierda.
Analizando con más detalle la caminata al azar uni-dimensional sus resultados
son los mismos que en la experiencia de arrojar una moneda al aire y resgistrando el
exceso de ‘caras’ (pasos hacia adelante) sobre ‘secas’ (pasos hacia atrás). La posición
más probable, luego de un considerable número de pasos, es siempre el origen, así
como un número igual de ‘caras’ y ‘secas’ es lo más probable. Posiciones extremas,
resultantes del caso que todos los pasos se toman en la misma dirección, son altamente improbables, y posiciones intermedias tienen probabilidades intermedias. La
distribución de posiciones alrededor del origen es simétrica ya que la chance de un
camino neto hacia adelante o hacia atrás (o de un exceso de ‘caras’ o de ‘secas’) es
la misma. A cada posición le corresponde una distancia desde el origen. Así una
distancia neta nula es la más probable, pero hay muchas distancia recorridas no-nulas
que tienen probabilidades …nitas no-nulas.
La distancia neta media cubierta en un camino al azar o, más exactamente, el
promedio de la distancia neta cubierta en cada uno de un gran número de caminatas
de este tipo, es, por cierto, cero, ya que estas distancias pueden ser tanto positivas
como negativas. Por su parte, el promedio de sus valores absolutos, o (la raíz de) el
promedio cuadrático de estas distancias netas, tienen valores …nitos. Estos valores los
llamaremos ‘distancias medias’ de aquí en adelante.
15
Por otra parte, la distancia media recorrida debe crecer con el tiempo, pero la
proporcionalidad es solamente con su raíz. Esto ha sido veri…cado experimentalmente
y las dos partes de la …gura de Perrin lo muestran cualitativamente. La longitud
media de los segmentos que unen las posiciones de la partícula es mayor en la parte
(b) que en la parte (a), pero no es diez veces mayor aunque corresponde a un número
de pasos diez veces mayor en tiempo.
b). Un análisis en detalle. Todas estas características terminan siendo también
las características de difusión, como se puede mostrar cualitativamente mediante la
…gura inferior de la lámina adjunta. Se trata de un esquema grá…co muy simple para
ilustrar como un movimiento al azar genera un ‡ujo neto de partículas si existe un
gradiente de concentración.
En la parte (a) el esquema indica que un sistema uni-dimensional presenta un
gradiente de concentración uniforme, con n partículas presentes al nivel cero, n + ¢n
a la distancia l debajo de ese nivel, y n ¡ ¢n a igual distancia l encima del mismo.
El gradiente de concentración es entonces
grad c =
n ¡ ¢n ¡ (n + ¢n)
¢n
=¡
2l
l
(2.1)
De acuerdo con Fick el número q de partículas que cruzan el nivel cero hacia arriba
en el tiempo t y por el área A es
q = ¡D (grad c) t A = ¡D (¡
¢n
¢n
)tA=D t
A
l
l
(2.2)
Calculemos ahora ese mismo número según un proceso al azar. Consideraremos
solo la componente vertical del movimiento de las partículas, que suponemos igual
para todas ellas de tal manera que cada una viaja la distancia media l hacia arriba o
hacia aba jo en el tiempo t. Debido al carácter al azar de esos movimientos la mitad
de las partículas presentes en cada nivel se mueven hacia arriba y la otra mitad se
mueve hacia abajo, como se indica en la parte (c).
El resultado es que solamente la mitad de las partículas que se encuentran a
distancias l o menores cruzarán el plano cero en un u otro sentido. Por aba jo del
plano de referencia el número de partículas a distancias l o menores está dado por el
producto del volumen l £ A por la concentración media (n + ¢n=2) (ver parte (b) de
!
la …gura). Entonces el número q que cruza el plano cero desde abajo hacia arriba en
el tiempo t y por el área A es la mitad de ese producto:
!
q=
1
l A (n + ¢n=2)
2
(2.3)
Ã
Similarmente el número q que cruza ese plano desde arriba hacia aba jo en ese mismo
tiempo t y por el mismo área A es
Ã
q=
1
l A (n ¡ ¢n=2)
2
(2.4)
ya que la concentración media encima del plano cero es (n ¡ ¢n=2).
El resultado neto es q, la diferencia entre estos dos números. Vale
!
Ã
q = q ¡ q=
17
l ¢n
A:
2
(2.5)
Comparando este valor de q con el dado por (2.2) según la ley de Fick resulta
D t
¢n
l ¢n
A=
A
l
2
(2.6)
y de aqui el valor de D es simplemente
D=
l2
;
2t
(2.7)
relación que indica que el coe…ciente de difusión está directamente proporcional al
cuadrado de la distancia media recorrida e inversamente proporcional al tiempo de
difusión. O, reescribiendo (2.7) como
p
l = 2Dt
(2.8)
se concluye que la distancia difusional efectivamente cubierta es proporcional a la raíz
del tiempo transcurrido, tal como se dedujo cualitativamente más arriba.
Esta relación se conoce como ley de Einstein para la difusión y el movimiento
browniano. Una deducción más rigurosa se da en la sección siguiente.
2.2. Interpretación estadística de la difusión. Ley de Einstein.
(a) Interpretación estadística. Einstein (1905) dió una interpretación estadística del coe…ciente de difusión, interpretación que resulta fundamental para entender
la naturaleza molecular de un proceso difusional y, en general, del movimiento browniano (A.Einstein Ann.Physik 17(1905)549; A.Einstein ”Investigations on the Theory of the Brownian Movement”, Metheun and Co., 1926, Dover, 1956; A.Einstein
Z.Elektrochem. 14(1908)235).
Existen varias deducciones, pero la más directa y menos cuestionable se deriva de
la distribución espacial uni-dimensional y temporal debida a un proceso difusional de
la concentración c(x,t) de una sustancia, cuya cantidad total M estaba ubicada en el
origen (x=0) al tiempo inicial t=0 (solución para una fuente puntual según la 2da.
ley de Fick; ver capítulo 5). Esta distribución es la siguiente::
M
c(x; t) = p
exp(¡x2 =4Dt)
2 ¼Dt
(2.9)
¿Puede usarse esta ecuación para contestar la pregunta acerca de qué distancia
recorrerá una cierta molécula en el tiempo t? La pregunta, así formulada, no tiene
sentido; la respuesta sería cualquier distancia entre -1 6x6 +1: Pero si se repite
muchas veces la observación, sí puede preguntarse acerca de la distancia media recorrida por dicha partícula en el tiempo t.
La probabilidad de encontrar la partícula entre las distancias x y x+dx al tiempo
t de la posición x=0 que ocupaba a t=0 se obtiene normalizando a (2.9) respecto de
todo el rango de la coordenada espacial x (para que la probabilidad de encontrar la
molécula en cualquier valor de x sea unitaria). Vale:
Z
+1
c(x; t) dx = M
¡1
18
y entonces se tiene:
c(x; t):dx
1
P (x):dx = R +1
= p
exp(¡x 2 =4Dt):dx
2
¼Dt
c(x; t) dx
¡1
La distancia media recorrida será
Z +1
Z +1
1
x¹ =
x:P (x):dx = p
x: exp(¡x 2 =4Dt):dx = 0
2 ¼Dt ¡1
¡1
(2.10)
(2.11)
(Para esta integral especial y otras que se usan más abajo ver sección 5.2.1). Esto
signi…ca que la distancia media recorrida es nula, lo cual es físicamente lógico (ver
sección anterior) pues las probabilidades de desplazarse hacia x>0 y hacia x<0 son
iguales.
Para conocer el recorrido real efectuado por la molécula sin considerar el sentido
hacia el cual se desplaza debemos analizar, por lo ya dicho también en la sección
anterior, la distancia cuadrática media recorrida x 2 . Se obtiene:
x2
=
=
)
Z
+1
1
2
Z
+1
x :P (x):dx = p
x2 : exp(¡x2 =4Dt):dx =
2 ¼Dt ¡1
¡1
p
Z +1
1
1
¼
p (4Dt)
y 2: exp(¡y 2 ):dy = p (4Dt)
= 2Dt
¼
¼
2
¡1
(2.12)
x 2 = 2Dt
Y de aquí surge la fórmula estadística de Einstein para el coe…ciente de difusión:
D = x2 =2t
(2.13)
(E instein)
relación que coincide con (2.7). Por lo tanto, la distancia cuadrática media recorrida
en el tiempo t es
dis tan cia difusional = xdif =
p
x2 =
p
2Dt
(2.14)
p
y esto signi…ca que el camino difusional medio recorrido es proporcional a t, tal
como ya se mencionó en la sección anterior. O sea, para recorrer difusionalmente
una distancia grande una molécula necesita mucho más tiempo que para recorrer,
proporcionalmente, distancias cortas.
Estas características quedan bien explícitas tomando como velocidad de difusión
v dif simplemente a
vdif ´ x dif = t
(2.15)
Entonces de (2.14) surge que
velocidad difusional = vdif
2D
=
=
x dif
r
2D
t
(2.16)
o sea, la velocidad difusional disminuye tanto a mayor distancia difusional recorrida
como a mayor tiempo de difusión, ya que dicha velocidad es inversamente proporcional
tanto a la distancia recorrida como a la raíz cuadrada del tiempo de difusión.
19
Una interpretación complementaria de D es la siguiente. Considérese que la
partícula avanza mediante saltos de longitud r y que la frecuencia de saltos es ¡
(=(nro. de saltos n)/(tiempo t)=n/t). Entonces
D=
x2
n:r2
r 2 :¡
=
=
2t
2:t
2
(2.17)
esto es, D es proporcional al cuadrado de la distancia de salto y a la frecuencia de los
saltos.
(b) Interpretación probabilistica. Por otra parte, la interpretación probabilística dada de la difusión es completamente congruente ya que la solución de la
fuente puntual (2.9)-(2.10) tiene la forma exacta de la distribución normal de Gauss:
P (x) = p
1
2¼¾ 2
exp[¡
(x ¡ ¹)2
]
2¾ 2
(2.18)
R +1
R +1
siendo ¹ el valor medio (= ¡1 x:P (x):dx) y ¾ 2 es la variancia (= ¡1 (x ¡ ¹)2
:P (x):dx).
Con ¹ = 0 queda, con ¾ 2 =x 2 ,
1
P (x) = p
2¼x2
exp[¡
x2
2x2
]
(2.19)
y comparando esta expresión con la solución difusional surge inmediatamente la
ecuación de Einstein, x2 = 2Dt:
Se puede demostrar que la fórmula (2.18) está directamente relacionada con el
movimiento al azar. Una formulación simple que lo muestra se da en la sección
siguiente.
(c) Análisis probabilístico de la caminata al azar. Analizaremos una caminata al azar unidereccional considerando pasos de igual longitud l y de igual duración
(intervalo) temporal ¿ . La cuestión es calcular la probabilidad que la partícula se
encuentre a la distancia x del origen luego de un tiempo t. En ese tiempo habrá
efectuado N pasos con N = t=¿ . Si N + de estos pasos fueron hacia la derecha y N ¡
son los pasos hacia la izquierda (N + + N ¡ = N ), entonces la distancia neta x desde
el origen es proporcional al número ‘efectivo’ de saltos s = N + ¡ N ¡ . Por lo tanto,
para llegar a x, vale
N+ =
1
(N + s)
2
y
N¡ =
1
(N ¡ s)
2
donde s = x=l:
(2.20)
(2.21)
El número total de diferentes formas de hacer una caminata de N pasos es 2N ,
ya que cada paso puede efectuarse hacia la derecha o la izquierda. Por su parte, el
número de formas de realizar la caminata en las cuales se efectúan exactamente N+
hacia la derecha es igual al número W de formas de elegir N+ objetos de un total de
N independientemente del orden de estos pasos en la secuencia de pasos:
W =
N!
N+ ! (N ¡ N+ )!
20
(2.22)
Como ejemplo consideremos una caminata de 4 pasos, la cual se puede efectuar
de 16 formas distintas. Hay 6 formas de tomar 2 pasos hacia la derecha y 2 hacia la
izquierda (6=4!/2!2!), y la probabilidad que la partícula esté nuevamente en el origen
luego de 4 pasos es 6/16. Por otra parte, la probabilidad que la partícula esté a la
distancia x=+4.l del origen es solamente 1/16, ya que todos los pasos deben hacerse
hacia la derecha y 4!/4!0!=1. El esquema completo de las distintas secuencias de
pasos es la siguiente:
¡¡ ¡¡
¡¡¡+
¡¡+ +
¡ +++
¡ +¡¡
¡++ ¡
+ +¡+
¡ ¡+¡
+ ¡¡¡
¡+¡ +
+¡+ ¡
+¡¡ +
+++ +
+ ¡++
+ ++¡
(2.23)
+ + ¡¡
Volviendo al caso general la probabilidad P(s) de estar en x (=s.l) luego de N
pasos es
número de formas con N+ hacia la derecha
=
número¸total de·formas
·
¸
N!
N!
=2 N = 1
=2N (2.24)
N + ! (N ¡ N + )!
( 2 (N + s))! ( 12 (N ¡ s))!
P (s) =
=
Esta fórmula es general y para evaluarla, como toda fórmula probabilística vale
para grandes números, es aplicable la fórmula de Stirling para los factoriales,
ln N ! = (N + 12 ) ln N ¡ N + ln (2¼)1=2 ;
(2.25)
Entonces se obtiene:
ln P (s)
= ln N ! ¡ ln( 12 (N + s))! ¡ ln( 12 (N ¡ s))! ¡ N ln 2 =
=
1
2
ln (2=¼N ) ¡ 12 (N + s + 1) ln(1 +
s
N
) ¡ 12 (N ¡ s + 1) ln(1 ¡ Ns ):
(2.26)
Los términos logarítmicos se pueden aproximar mediante
ln (1 § z) t §z ¡ z2
ya que siempre s<<N. La expresión anterior se simpli…ca entonces a:
ln P (s) =
1
2
s2 1 s2
ln (2=¼N )¡
+
N 2 N2
1
2
)
P (s) =
µ
2
¼N
¶1=2
exp
µ
¡ 12
s2
N
¶
; (2.27)
donde se ha despreciado el término s2 =N 2 .
La ec.(2.27) da la probabilidad P(s) para s saltos ‘efectivos’. Para obtener la
probabilidad P(x) para la distancia x (=s.l) debemos reconocer que s es una magnitud
par (la magnitud s (= N+ ¡ N ¡) varía de a dos ya que si un salto no es hacia la
derecha lo es hacia la izquierda). Por lo tanto, P(x) corresponde a x comprendido
entre s.l y (s+2).l, o sea, dx=2l.ds y vale
P (x) dx = P (s) ds = P (s) dx=2l
21
y resulta
P (x) =
µ
1
2¼l2 N
¶1=2
exp
µ
x2
¡ 12 2
l N
Recordando además que N = t=¿ se obtiene …nalmente:
µ
¶
³ ¿ ´1=2
¿ x2
P (x) =
exp ¡ 2
2¼l2 t
2l t
¶
(2.28)
(2.29)
expresión que es exactamente del tipo gaussiano dado por (2.19)y por2.10.. Por lo
tanto, comparando con (2.19), o calculando directamente x 2 , se deduce
Z 1
2
x =
x 2 P (x) dx = l2 t=¿ (= 2Dt)
¡1
donde la última relación se ha escrito según (2.13). De aquí se deduce nuevamente
D=
l2
;
2¿
la expresión primaria (2.7) de Einstein para D (Recuérdese las de…niciones de l y ¿
utilizadas en esta sección).
Con lo presentado aquí queda demostrado la naturaleza probabilístico-estadística
de la caminata al azar y del proceso difusional y su íntima connección.
2.3. Propiedades del co e…ciente de difusión en función de las características
de las partículas.
2.3.1. Gases.
Las características escalares y estadísticas descriptas en las secciones anteriores para
el fenómeno de difusión se con…rman (o se derivan) principalmente a partir de las
propiedades generales de gases, especialmente sus propiedades de transporte (difusión,
conducción térmica, viscosidad). De estas propiedades se derivan también dependencias del coe…ciente de difusión con las características moleculares (tamaño y masa) de
las partículas que difunden.
Asi, es clásica la observación de Graham que la velocidad de efusión de un gas
(escape de un gas a través de un agujero pequeño en la pared del recipiente que lo
contiene) es inversamente proporcional a la raíz de la masa m de las moléculas del
gas (ley de Graham):
1
v(ef usi o¶n) / p ;
(2.30)
m
es decir, partículas más pesadas efunden (difunden) más lentamente que partículas
más ligeras.
La Teoría Cinética de los Gases explica perfectamente esta y otras propiedades
de transporte de los gases (ver capítulo correspondiente). Así para el coe…ciente de
difusión Di de un gas puro i esta teoría entrega la siguiente expresión fundamental:
r
1
RT RT 1
Di =
(gas puro)
(2.31)
2
¼di ¼M i N Av P
22
Esta fórmula señala que el coe…ciente de difusión de las partículas del gas i es a)
inversamente proporcional a la raíz de las masa molar Mi (ley de Graham), b) inversamente proporcional al cuadrado del diámetro di de las moléculas, c) inversamente
proporcional a la presión P del gas, d) directamente proporcional a la potencia 3/2
de la temperatura termodinámica T del gas. Entonces la difusión gaseosa será más
lenta para partículas más grandes y más pesadas, y a mayor presión (más colisiones),
pero se hace más rápida a mayor temperatura.
La fórmula (2.31) corresponde a un gas puro y por ello el coe…ciente Di se denomina
coe…ciente de autodifusión del gas i. Se introduce esta denominación para diferenciar
este proceso del fenómeno de (inter-)difusión en mezclas de gases. En este último
proceso interdifunden (se mezclan) expontáneamente al menos dos gases a presión P y
temperatura T dadas, y aparecen colisiones entre partículas de distintas características
físicas. Para el coe…ciente de interdifusión D que caracteriza este proceso la teoría
entrega la siguiente expresión (fórmulas de Meyer y de Stefan-Maxwell) (xi: fracción
molar):
D
=
=
x 2 D1 + x1 D2 =
s
1 1
RT RT 1
2
2 ¼d12 ¼¹12 NAv P
[6= f (x)]
donde
d12 ´ r1 + r2
(2.32)
(M eyer)
(Stef an ¡ M axwell)
1
1
1
´
+
¹12
M1
M2
y
(2.33)
(2.34)
d 12 es el diámetro de choque entre moléculas distintas de radios r 1 y r 2 , y ¹12 la
masa molar reducida de la mezcla de los gases 1 y 2, mientras P y T son propiedades
de estado de la mezcla. Se observa que en D se mantiene la proporcionalidad con
la inversa de tamaño y masa de las partículas, aunque ahora combinando en forma
especial las propiedades de ambos componentes de la mezcla gaseosa, pero D es, según
la fórmula de Stefan-Maxwell, independiente [6= f(x)] de la composición de la mezcla,
un hecho veri…cado experimentalmente.
2.3.2. Fases condensadas. Movilidad y fricción en difusión.
(a) Difusión molecular. Para sistemas condensados la interpretación del coe…ciente de difusión se debe plantear en forma distinta, más hidromámica, ya que no
es aplicable a la Teoría Cinética.
De acuerdo con (1.21) y (1.22) se puede escribir la ley empírica de Fick para el
caso de una sustancia 2 a dilución in…nita en un medio (solvente) de índice 1 de la
siguiente manera simple:
J2 = c2(v2dif ¡ v1 ) = ¡D±2 grad c2
(2.35)
(F ick)
donde D±2 es el coe…ciente de interdifusión en esa situación:
D±2 ´ lim D
c 2!0
1(1)
(= D2
(2.36)
)
De aqui se deriva para la velocidad de difusión:
v dif
¡ v1 = ¡D2±
2
grad c2
1 dc2
D±
= ¡D±2
= 2
c2
c2 dx
RT
23
·
¡RT
d ln c2
dx
¸
(2.37)
donde para obtener la última expresión se ha multiplicado y dividido por RT y reagrupado. Esta última expresión se puede comparar con la relación general del movimiento
uniforme, por la cual la velocidad es proporcional a la fuerza impulsora, es decir,
v2dif ¡ v 1 = B2 X2dif
(2.38)
donde X2dif indica la fuerza impulsora de difusión y la movilidad difusional molar B2
es la constante de proporcionalidad correspondiente, de…nida según
B2 ´
v dif
¡ v1
2
(2.39)
dif
X2
Comparando (2.37) y (2.38) se deduce explicitamente que la fuerza impulsora molar
de difusión es
d ln c2
RT dc2
X2dif ´ ¡RT
=¡
(2.40)
dx
c2 dx
(verifíquese dimensiones) y entonces queda la siguiente expresión general para el coe…ciente de difusión en esta situación:
D2± = RT B±2 ;
(2.41)
donde se introducido el supraíndice (± ) en B2 .
Esta expresión se puede adjudicar a Einstein, aunque éste utilizó la formulación
inversa de (2.38). Introduciendo el coe…ciente de fricción molar F2 escribe (2.38) como
³
´
X2dif = F2 v2dif ¡ v 1
(2.42)
y, por lo tanto, vale
F2 =
1
B2
(2.43)
Combinando (2.43) con (2.41) se obtiene la otra fórmula muy conocida de Eisntein
para el coe…ciente de difusión:
D±2 =
RT
F 2±
(= RT B±2 )
(Einstein)
(2.44)
Esta relación señala que D es inversamente proporcional a la resistencia (fricción) que
sufre la partícula en el medio en que se mueve. La misma se torna aún más útil si
se la combina con alguna expresión explícita de F 2 como, por ejemplo, la relación de
Stokes para el movimiento de una esfera sólida en un medio viscoso:
F 2 = N Av 6¼ ´ 1 r2
(2.45)
siendo ´ 1 la viscosidad del medio y r2 el radio de la esfera. Con (2.44) y (2.45) resulta
la fórmula de Eisntein-Stokes:
D2± =
RT =N Av
kT
=
6¼ ´ 1 r2
6¼ ´ 1 r2
(E instein ¡ Stokes)
(2.46)
(k(=R=NAv ) constante de Boltzmann), donde r2 es ahora el radio de la partícula
que difunde. La fórmula (2.46) es de gran aplicación en la literatura para estimar
coe…cientes de difusión en estas condiciones (dilución in…nita) si no se tienen otros
24
datos. D2± es entonces en medios ‡uidos condensados proporcional a la inversa del
radio de la partícula que difunde y también invesamente proporcional a la viscosidad
del medio en el cual se mueve.
Una aplicación clásica de ambas ecuaciones de Einstein, (2.13) y (2.44)-(2.46),
la realizó Perrin (J.Perrin “The atoms”, Constable and Co.Ltd, 1923) para evaluar
el movimiento browniano de partículas de gutagamba dado por la …gura dada más
arriba. Combinando ambas ecuaciones resulta:
l2
RT =NAv
=
4t
6¼ ´ 1 r2
(2.47)
y en esta relación todas las magnitudes son medibles salvo la constante de Avogadro
N Av : Despejando de aquí N Av se tiene
NAv =
RT 4t
6¼ ´ 1 r2 l 2
(2.48)
y mediante esta fórmula Perrin obtuvo de sus observaciones de microscopio valores
correctas de NAv del orden de v 1023 ; resultado que señala la realidad física de las
relaciones presentadas aquí.
Sin embargo varias observaciones deben hacerse respecto de todas estas relaciones,
las cuales deben considerarse como ecuaciones ideales para difusión. Así la fuerza
impulsora (2.40) es una expresión ideal (para solución diluída ideal); según la TPI
(ver capítulos siguientes) la fuerza impulsora real es el gradiente de potencial químico
correspondiente. Por su parte, la ec.(2.44) vale para un medio puro (solvente dado);
se demuestra que para medios complejos conteniendo varias sustancias (p.ej. otros
solutos a concentraciones …nitas) en esta relación debe reemplazarse el coe…ciente
de fricción f 2 por una sumatoria de los coe…cientes de fricción del soluto 2 con las
distintas especies moleculares k presentes en el medio, esto es,
X
F2 )
F 2k
(2.49)
k
En cambio, (2.41) no se modi…ca y la in‡uencia de las distintas especies presentes
sobre la movilidad de difusión es dada por (2.49) según (2.43).
Por otra parte, los coe…cientes númericos en muchas de estas relaciones no son
completamente exactos; en particular el valor 6¼ en la relación (2.45) de Stokes es
discutible ya que, por un lado, es una ley macroscópica (movimiento en un medio
continuo) que se aplica a nivel microscópico, nivel en el cual el medio (solvente) es
discreto, y, por otro, muchas partículas no tienen forma esférica. Se recomienda
la lectura del artículo ”Molecular volumes and the Stokes-Einstein equation.” de
J.T.Edward, J.Chem.Ed. 47(1970)261-270. (Ver …guras y texto de Sección 3.3.2).
Todas las relaciones anteriores valen para partículas que difunden sin interaccionar
(salvo por colisiones) con otras partículas, especialmente a dilución in…nita.
(b) Difusión de especies iónicas. Por su parte la aplicación de estos conceptos
a sistemas con partículas que interaccionan es más compleja. Esto vale especialmente
para soluciones que contienen iones, es decir, especies cuyas cargas eléctricas generan interacciones de largo alcance. El caso más simple corresponde al caso (d) de
la sección 1.2.3, es decir, a una solución de un solo electrolito (sal) binario simétrico
como soluciones acuosas de NaCl o CuSO4 . Como ya se ha mencionado allí, el hecho
25
macroscópico a tener en cuenta es que por difusión no se transportan cargas eléctricas (ec.(1.14)) y la consecuencia es que los dos tipos de iones difunden a la misma
velocidad (ec.(1.15)). El coe…ciente de difusión corresponde a la sal en cuestión y
este coe…ciente es función de las movilidades iónicas propias de los dos iones que la
constituyen. A dilución in…nita la fórmula para electrolitos 1:1 se debe a Nernst:
D± = 2
RT o ¸ ±c o¸ ±a
[
]
F 2 o ¸ ±c + o ¸±a
(N ernst 1888)
(2.50)
El hecho macroscópico que por difusión no se transportan cargas eléctricas, razón
por la cual los dos iones difunden a la misma velocidad efectiva, tiene su contraparte
microscópica. En presencia de inhomogeneidades de concentración del electrolito, si
sus cationes y aniones se mueven con distintas velocidades los centros espaciales de
cargas catiónico y aniónico ya no serán coincidentes e instantáneamente aparecerá
un potencial eléctrico que se opone a esa separación de cargas. Este potencial se
denomina potencial de difusión, un concepto también introducido por Nernst (1888))
(ver capítulo de difusión de electrolitos). El mismo frena al ión más rápido y acelera al
ión más lento y determina entonces localmente que ambos tipos de iones se muevan por
difusión con la misma velo cidad, y consecuentemente un solo coe…ciente de difusión,
dado por (2.50) a dilución in…nita, caracteriza estos sistemas.
Finalmente debe señalarse que en la literatura y los libros de texto se introduce un
coe…ciente de difusión Di± para iones según una relación llamada de Nernst-Einstein,
a saber,
±
D±i
o ¸i
=
(Nernst-Einstein)
(2.51)
RT
jzij F 2
relación que formalmente supone que el mecanismo difusional y el mecanismo migratorio eléctrico de un ión son idénticos. Esta conclusión es errónea. Aunque la ec.(2.51)
sea formalmente correcta, el coe…ciente de difusión iónico Di± no tiene sentido físico
ya que los iones no difunden como tales, ya que este movimiento está condicionado
por el potencial de difusión, según lo visto más arriba. (Mayores detalles al respecto
se dan en el capítulo de difusión de electrolitos.).
2.3.3. Interpretación por correlación de velocidades.
A la relación (2.13) de Einstein y al coe…ciente de difusión se le puede dar todavía
otra interpretación general muy interesante. Para presentarla se reescribe (2.13) más
explícitamente de la siguiente forma.
D = lim
t!1
< (x(t) ¡ x(0))2 >
2t
(2.52)
donde x(t) es la posición de la partícula al tiempo t si al tiempo t=0 estaba en x(0).
<...> indica ahora un promedio sobre todo el conjunto de partículas en el intervalo
de tiempo t y se toma ese promedio para tiempos su…cientemente grandes.
Formalmente la distancia (x(t) ¡ x(0)) está dada por la siguiente integral:
¢x(t) = x(t) ¡ x(0) =
26
Z
t0=t
t0=0
v(t0 ):dt0 ;
(2.53)
donde v(t) es la velocidad de la partícula, y, por lo tanto, la distancia cuadrática
media viene dada por la siguiente integral doble:
< (x(t) ¡ x(0))2 > =
Z
t00 =t
t00 =0
Z
t0 =t
t0 =0
< v(t0 ) ¢ v(t00 ) > dt0 dt00
(2.54)
En esta fórmula aparece el promedio del producto escalar de las velocidades de la
partícula a tiempos t’ y t”, función que se denomina función temporal de correlación
de velocidades,:
F (t) ´ < v(t0 ) ¢ v(t00 ) > :
(2.55)
Para precisar el signi…cado de este producto escalar de los valores de la velocidad
de una partícula a dos tiempos distintos se debe tener en cuenta que la velocidad de
la partícula cambia a raíz de las colisiones con otras partículas y que colisiones bien
separadas en el tiempo son estadísticamente independientes, y que en esas condiciones
ese producto es nulo. Contrario sensu, ese pro ducto, es decir, la ‘correlación’ entre
valores de la velocidad a dos tiempos t0 y t00 solo será no-nulo para intervalos de
tiempo del orden de la duración ¿ c de una colisión o, a lo sumo, de dos o tres colisiones
seguidas, o sea, para intervalos de tiempo muy cortos. Esto es, este producto es en
realidad sólo una función de la diferencia ¿ = t00 ¡t0 ; el intervalo de tiempo considerado,
y esta función es muy aguda y …nita alrededor de ¿ = 0 y nula para j¿ j > ¿ c :
Además, al tratarse de un conjunto de partículas en equilibrio esta función de
correlación es independiente de la escala de t (eje de tiempo) e invariante con la
inversión del tiempo, es decir, es una propiedad estacionaria del sistema, o sea,
<
=
v(t0 ) ¢ v(t00 ) > = < v(0) ¢ v(t00 ¡ t0 ) > =
< v(0) ¢ v(t0 ¡ t00 ) > = < v(0) ¢ v(¿ ) >
(2.56)
Esta propiedad permite precisar el signi…cado físico de (2.54). Para introducirla es
conveniente cambiar las variables de integración por ¿ = t00 ¡ t0 y # = t0 + t00 y se
obtiene
Z t00 =t Z t0 =t
Z ¿ =t Z #=2t
0
00
0
00
< v(t ) ¢ v(t ) > dt dt =
< v(0) ¢ v(¿ ) > d¿ d# =
t 00 =0
t0 =0
¿ =t
Z
¿ =0
<
v(0) ¢ v(¿ ) > d¿
Z
¿ =0
#=2t
#=0
Z ¿ =t
d# = 2t
#=0
¿ =0
< v(0) ¢ v(¿ ) > d¿
(2.57)
(el jacobiano del cambio de variables es unitario). Con este resultado se deduce
inmediatamente de (2.54) y (2.52) que
< (x(t) ¡ x(0))2 >
D = lim
=
t!1
2t
Z
¿ =1
¿ =0
< v(0) ¢ v(¿ ) > d¿
(2.58)
R
La integral F (¿ )d¿ ; denominada precisamente integral temporal de correlación de
velocidades, opera sobre todo el rango del intervalo de correlación y, por lo dicho más
arriba acerca de la función F(¿ ), su integral es …nita y toma rápidamente, para ¿ >
¿ c ,un valor constante, valor que depende solamente del mecanismo de las colisiones
moleculares o, más generalmente, del mecanismo del movimiento de las partículas.
La fórmula (2.58) se conoce como fórmula tipo Green-Kubo, por los autores (Green
(1956), Kubo (1957)) que la formularon por primera vez. Parecidas fórmulas se
27
pueden plantear para las conductividades térmica y eléctrica, y, por la Teoría de
Respuesta Lineal (Termodinámica Estadística de No-Equilibrio), se puede generalizar
esta formulación para los coe…cientes fenomenológicos de conductancia ! Lij (RaineriTimmermann (1989)).
____________________
28
Q FI I- 2M 4C 2 - F I - U BA ; D r.E.O .T im me rm an n
3. Descripción fenomenológica de la difusión.
3.1. Flujos y fuerzas para transporte de materia.
En la Parte I, secciones 4 y 5, se ha discutido en general las fuerzas y ‡ujos fenomenológicas que surgen del balance de entropia en sistemas continuos y que determinan la función de disipación. Especializando estas consideraciones para el transporte
de materia, y especialmente para el caso de difusión, estas fuerzas quedan reducidas
al gradiente isotérmico-isobárico del potencial químico,
(3.1)
XJ = ¡gradT ;P ¹J ´ YJ
fuerza para la cual se reserva el símbolo Y J . En condiciones isotérmicas e isobáricas
y en equilibrio mecánico para estas fuerzas vale la siguiente relación, que coincide con
la conocida ecuación de Gibbs-Duhem para los potenciales químicos,:
X
X
cJ YJ =
cJ (¡gradT ;P ¹J ) = 0 (eq.mec. y ec. Gibbs-Duhem)
(3.2)
J
J
o sea, para N componentes (SMI) hay solo (N-1) fuerzas independientes.
En equilibrio mecánico la función de disipación ª resulta independiente del SR en
que se expresan los ‡ujos y para el presente caso tenemos
X
X
!J cQ
ªdif =
con ! Y J = YJ ¡
YQ
(3.3)
! JJ Y J =
!J J !YJ
cJ ! Q
J
J 6=Q
expresión de la cual ya se ha eliminado el ‡ujo dependiente (J=Q)(ver Parte I ec.5.32).
Recordemos que la relación general de vínculo entre ‡ujos es
X !J
(I-ec.5.6)
(3.4)
! JJ = 0
cJ
J
Para el SR natural de difusión, el de volumen …jo, vale
X
VJ w JJ = 0 y ! J = cJ V J ;
(3.5)
J
y reemplazando estas relaciones en las expresiones precedentes se obtiene (con Q=1)
ªdif =
P
J6= 1 w JJ w YJ
con
w YJ
´ (¡gradT ;P ¹J ) ¡
VJ
(¡gradT ;P ¹1 ) (3.6)
V1
siendo entonces w Y J la fuerza fenomenológica independiente de la difusión, magnitud
que no es simple sino una diferencia de gradientes de potenciales químicos.
La alternativa es el SR de especie, donde elegimos como especie de referencia al
solvente (Q=1). Entonces
1J1
=0
con
(3.7)
! J = 0 (J 6= 1); ! 1 = 1
y ªdif toma la forma simple siguiente:
P
ªdif = J 6=1 1 JJ (¡gradT ;P ¹J ) con
1 JJ
´
w JJ
¡
cJ
c1
w J1
= c1 (v J ¡ v1 )
(3.8)
y para este SR la fuerza es simplemente
1 YJ
´ Y J = ¡gradT ; P ¹J
29
(3.9)
3.2. Ecuaciones fenomenológicas (de conductancia) para la difusión.
Ambas alternativas (conductancia: ‡ujos en función de fuerzas, o resistencia: fuerzas
en función de ‡ujos) se pueden utilizar para formular las ecuaciones fenomenológicas
(EF) para el transporte difusional.
En el formalismo de conductancia se tiene, siempre con J; K 6= 1 (componente 1
como dependeiente):
(a) SR de volumen …jo :
w JJ
=
P
K 6=1 w LJ K
[(¡gradT ;P ¹K ) ¡
VK
(¡gradT ;P ¹1 )]
V1
(3.10)
donde los coe…cientes fenomenológicos (CF) tienen las siguientes propiedades (ver
ec.I-5.40):
p
(3.11)
w LJ J > 0;
w LJ K = w LK J ·
w LJ J ¢ w LK K
(b) SR de solvente o especie …ja (componente 1):
1 JJ
=
donde
1 LJ J
> 0;
1 LJ K
=
1 LK J
P
K 6=1 1 LJK
·
p
1 LJ J
¢
(¡gradT ;P ¹K )
1 LK K
( 1 L11 =
(3.12)
1 L1K
=
1 LJ1
´ 0)
(3.13)
3.3. Interpretación fenomenológica del coe…ciente de difusión (sist.binarios).
3.3.1. Descripción general.
Por todo lo visto se puede expresar el ‡ujo difusional w J2 del soluto tanto en una
formulación empírica (ley de Fick) como en una formulación fenomenológica y corresponde establecer la relación entre ambas. Entonces w J2 vale:
w J2
= ¡D grad c2 = ¡
|
{z
}
|
e xp r.e m p íric a
w L22
V2
(gradT ;P ¹2 ¡
gradT ;P ¹1 )
V1
{z
}
(3.14)
e xp r.f en om e n ológ ica
utilizando la formulación de conductancia. (La correspondiente de resistencia se desarrolla en la sección 2.4)
Recordando las relaciones termodinámicas auxiliares usuales,
c1 gradT ;P ¹1 + c2 gradT ;P ¹2 = 0
y
1 = c1 V 1 + c2 V2 ;
(3.15)
la fuerza fenomenológica w Y 2 toma la forma simple siguiente (nota: argumento solo
válido para sistemas binarios):
¡ wY2
=
=
V2
gradT ; P ¹1 =
V1
c2 V 2
gradT ; P ¹2
(1 +
) gradT ; P ¹2 =
c1 V 1
c1V 1
gradT ;P ¹2 ¡
30
(3.16)
Con estas relaciones la expresión del ‡ujo del soluto en una solución o mexcla
binaria queda:
w J2
gradT ; P ¹2
= ¡D grad c2 = ¡ w L22
|
{z
}
c V
|
{z 1 1 }
ex p r.e mp íric a
(sist:binarios)
(3.17)
e xp r.fe n om e n ológ ica
donde la primera es la clásica expresión empírica de Fick y la segunda la formulación
termodinámico-fenomenológica más directa. La primera indica que la fuerza impulsora es el gradiente de la concentración c2 y la segunda que dicha fuerza es el gradiente
del potencial químico ¹2 del soluto dividido por la fracción de volumen c1 V1 del solvente.. Los respectivos coe…cientes de proporcionalidad con el ‡ujo w J2 del soluto son
distintos y es evidente que si se puede derivar la relación entre dichas fuerzas también
se podrá formular la relación entre esos coe…cientes, el coe…ciente de difusión D y el
fenomenológico w L22 :
Se sabe que el potencial ¹2 depende de la concentración c2 y esa dependencia se
puede explicitar de la siguiente manera completamente general
·
¸
d¹2
(c)
(c)
gradT ;P ¹2 = ¹22 grad c2 con ¹22 ´
(sist:binarios)
(3.18)
dc2 T ;P
( c)
donde la derivada ¹22 expresa esa dependencia. Con esta relación la expresión del
‡ujo del soluto queda:
wJ 2
= ¡D grad c2 = ¡
w L22
gradT ;P ¹2
= ¡[
c1 V1
(c)
w L22
¹22
] grad c2
c1 V1
(3.19)
Por comparación resulta la siguiente expresión para D:
( c)
D=
w L22
¹22
=
c1 V 1
w L22
c2
(c)
[c2 ¹22 ]
c1 V1
(3.20)
En la segunda expresión se ha multiplicado y dividido por c2 para introducir la movilidad fenomenológica w B22 según
w B22
´
w L22
c2
(3.21)
(> 0);
y entonces resulta la siguiente relación fundamental para el coe…ciente de difusión:
(c)
D=
w B22
[c2 ¹22 ]
c1 V1
(3.22)
Esta importante ecuación da la interpretación fenomenológica fundamental para
D. Muestra que este coe…ciente empírico de transporte es una magnitud compuesta,
integrada por dos factores, uno cinético (de transporte), la movilidad w B22 , y otro
(c)
termodinámico, [c2 ¹22 ]=(c1 V1 ), integrado por varios parámetros termodinámicos:
Este último factor se conoce como factor termodinámico de la difusión (FTD) y tiene
un efecto importante y determinante sobre el comportamiento con la concentración
de D. Por lo tanto, como conclusión completamente general se obtiene:
coef. de difusión
= movilidad difusional
31
£
factor termodinámico
(3.23)
Por (3.11) la movilidad difusional w B22 dada por (3.21) es siempre positiva ; por
su parte, el FTD es también siempre positivo (ver I-3.44) para fases (materialmente)
estables. Por lo tanto, todas las magnitudes que, según (3.22), determinan el coe…ciente de interdifusión D son todas positivas, y en consecuencia también D es siempre
positivo para fases estables:
D>0
(f ases estables)
(3.24)
El factor termodinámico de la difusión, FTD, aparece en (3.22) por el planteo
termodinámico-fenomenológico usado en (3.14), el cual, como se ha visto, se deriva
directamente del 2do. Principio. Su papel en la interpretación del comportamiento de
D es importante, como ya se ha dicho, y el mismo está integrado exclusivamente por
parámetros termodinámicos dados por la Termodinámica de Equilibrio (recuérdese el
postulado del equilibrio local). Las características del FTD se analizan en detalle más
adelante y en los Apéndice I y II.
Es conveniente tratar en primera instancia las propiedades de D para sistemas
termodinámicammente ideales.
3.3.2. Sistemas ideales. Relaciones de Einstein y de Stokes-Einstein.
Los sistemas termodinámicos denominados ideales son de dos tipos: a) las soluciones
diluídas ideales, que siguen una ley tipo Henry, y b) las mezclas ideales, que siguen
leyes tipo Raoult.
Soluciones diluídas ideales. Para estas soluciones el potencial químico de cada
soluto responde a expresiones de estado tipo de dilución in…nita (estado Henry) como,
p.ejemplo, la siguiente en la escala de molaridades:
¹2 = ¹¦2 + RT ln
c2
cy2
(sol:dil:ideales; c2 ! 0)
(3.25)
donde ¹¦2 es el potencial tipo molar del soluto y cy2 = 1 mol=dm3 : De aqui
d¹2
RT
jT ;P =
dc2
c2
(3.26)
y sustituyendo en (3.18) resulta para la fuerza impulsora termodinámica la siguiente
expresión simple:
µ
¶
d¹2
RT
gradT ;P ¹2 =
jT ;P grad c2 =
grad c2
(3.27)
dc2
c2
expresión que coincide con la dada por (2.40) sobre la base de una discusión cualitativa. Por otra parte, sustituyendo (3.26) en la primera expresión de (3.20) y reagrupando se deduce
µ
¶
RT
RT
w L22
D=
=
(3.28)
w B22
c1 V 1
c2
c1 V1
donde se ha introducido la movilidad fenomenológica (3.21). Esta fórmula vale especialmente para soluciones muy diluídas (c2 ! 0; c1 V 1 ! 1) y entonces se debe escribir
32
(ver ec.(1.22)):
D±2
´ lim c2!0 D
(=
1(1)
D2
)
= RT
µ
w L22
c2
¶±
±
= RT 1 B22
(3.29)
donde se ha introducido el supraíndice (± ) para indicar c2 ! 0: Además en esa
situación w ! v1 y se ha sustituído w B ±22 ! 1 B±22 , la movilidad referida al sol±
vente (índice 1), y 1 B22
:es la movilidad a dilución in…nita del soluto 2 en el medio
(solvente) 1. Esta expresión (3.29) es una ley límite general y es la justi…cación
termodinámico-fenomenológica de la relación (2.41) de Einstein.
Las relaciones precedentes corresponden al nivel molar y es adecuado expresarlas a
nivel molecular. Hemos utilizado las siguientes expresiones (índice 1 para el solvente):
v 2 ¡ v1 =
1 L22
c2
(¡gradT ; P ¹2 ) =
1 B22
(¡gradT ;P ¹2 ) con
1 B22
=
donde, como ya se ha visto, la de…nición de la movilidad molar es
v2 ¡ v1
movilidad difusional molar: 1 B22 =
¡gradT ;P ¹2
1L 22
c2
(3.30)
(3.31)
Para obtener movilidades moleculares debe dividirse la fuerza molar (¡gradT ;P ¹2 )
por el número de Avogrado N Av para obtner una fuerza por molécula y entonces se
obtiene
v2 ¡ v 1
movilidad difusional molecular: 1 b 2 = NAv 1 B22 =
(3.32)
¡gradT ; P ¹2
[
]
N Av
Con R=N Av k (k: cte. de Boltzmann) la expresión (3.29) de D toma la forma
siguiente simple (2.44) de Einstein:
D±2 =
RT
kT
N Av 1 B±22 = kT 1 b ±2 = ±
NAv
f2
(3.33)
donde la tercera relacion surge de (2.43) con f2 (=F2 =N Av ), el coe…ciente de fricción
molecular. La fórmula de Einstein (quién no la dedujo, como ya se dijo, con la
formulación termodinámica irreversible dada aquí, ya que no estaba desarrollada en
esa época) establece entonces la siguiente regla general
kT
coef: f ricci¶
o n molecular
(3.34)
Como ya se señaló en la sección (2.3.2) la relación de Einstein se puede combinar
con la ley de Stokes y se obtiene la conocida relación de Stokes-Einstein:
coef: difusi¶on l¶imite = kT £ movilidad molecular =
) (Einstein):
D±2 =
kT
kT
=
f2±
6¼´ o r2
(Stokes-Einstein)
(3.35)
Y de aqui se obtiene una clásica regla de invariancia para el coe…ciente de difusión,
equivalente a la regla de Walden para la conductividad equivalente,:
D± ´ o
= cte:
T
[Walden : ¤ ± ´ o = cte:]
33
(3.36)
donde ´ o es la viscosidad del solvente puro.
Para la ley de Stokes-Einstein valen las mismas observaciones que fueron hechas
para la aplicación de la ley de Stokes a las conductividades iónicas (ver Parte IIb,
sección 2.4). La discusión se centra en qué valor debe usarse para r2 y cual es el
valor numérico a aplicar en lugar de 6¼ para el caso de partículas no-esféricas. Se
recomienda la lectura del artículo ”Molecular volumes and the Stokes-Einstein equation.” de J.T.Edward aparecido en J.Chem.Ed. 47(1970)261-270.
En la lámina adjunta se dan algunas de las …guras del artículo de Edwards. La
primera señala el factor de corrección a aplicar para los casos en que las dimensiones
de la partícula no son esféricas. Si dos dimensiones son del mismo orden y la tercera
tiende a ser (a) bastante menor o (b) bastante mayor, se obtienen para la partícula
con…guraciones que tienden a (a) una forma de disco (oblate) o (b) una forma de
cigarro (prolate), y la fricción con el medio se di…culta y debe aplicarse el factor
indicado por la …gura. Por otra parte, si el tamaño de la partícula que difunde pasa
a ser del mismo orden que las partículas del solvente las bases macroscópicas (medio
continuo) ya no se cumplen y el factor 6 en la fórmula de Stokes ya no es seguro.
Edwards analiza coe…cientes de difusión de distintas sustancias, cuyo radio de van
der Waals se conoce, en dos solventes, tetracloruro de carbono (segunda …gura) y
agua (tercera …gura). Las …guras presentan el número n (6= 6) de Stokes a utilizar en
la expresión de Stokes:
n = D ¼´ o r2 =kT
(3.37)
en función de los radios de las partículas que difunden y se observa en ambos casos
que n<6 para radios menores que 6 Å
Mezclas ideales. Para estas mezclas de componentes completamente miscibles el
potencial químico de cada componente (i=1,2) responde a la expresión correspondiente al estado tipo de componente puro (estado Raoult):
¹i = ¹²2 + RT ln x 2
(3.38)
(mezclas ideales)
donde ¹²2 es el potencial del componente puro. De aqui (i = 1; 2; j = 2; 1)
µ
¶
d¹i
RT
d¹i
d¹i dxi
RT V¹ 2
x j RT
jT ;P =
)
ci
= ci
= ci
=
²
dx i
xi
dci
dxi dci
x i Vj
cj V j²
(3.39)
donde se ha utilizado las siguientes relaciones para mezclas ideales (con x i = ciV¹ ):
xi
xi
ci = ¹
=
²
V (xi )
x1 V 1 + x 2 V2²
)
V j²
cj V j²
dci
= ¹2 =
dxi
V
xj V¹
(3.40)
siendo V i² es el volumen molar del componente i puro.
Sustituyendo en (3.22) queda
id
D (x)
µ
=
w B22
(c1 V1² )
¶
(c)
[c2 ¹22 ]
=
µ
w B22
(c1 V 1² )
¶id
x 1 RT
=
c1 V1²
µ
w B11
(c2 V2² )
¶ id
x2 RT
c2 V 2²
(3.41)
expresión que se ha escrito para ambos componentes (intercambiando subíndices), ya
los dos son equivalentes en mezclas binarias.
El supraíndice (id ) indica situación ideal, indicación que introduce un problema.
Se ha supuesto idealidad termodinámica, que se sabe describir (ec.(3.38)), pero, al
35
Fórmulas de estimación del coeficiente de difusión.
Stokes-Einstein
k T 1
Do(B)
(SE) =
A
6π ηB rA
a) Wilke C.R. and Chang P
T ΦBMB
Do(B)
= 7.4*10 −8
A
ηB VA0.6
r A = molecular radius of solute A
ηB = viscosity of solvent B
b) Sitaraman R., Ibrahim. S.H., Kuloor N.R
0.93
 M 0.5 T ∆L1 / 3 
D
= 5.4*10  B 0.5 B0.3 
 ηB VA ∆L A 
c) King C.J., Hsueh L., Mao K.-W
o(B)
A
−8
Do(B)
= 4.4*10 −8
A
T
ηB
 VB 
V 
 A
1/6
 ∆HB 
 ∆H 
 A
1/2
d) Edwards J.T.
k T 1
6 o(B)
Do(B)
=
=
D A (SE)
A
n SE π ηB rA n SE
e) Tyn M.T. and Calus W.F
1/6
T  VB 
ηB  VA2 
f) Hayduk W., Minhas B.S.
1.47
1
−8 T
Do(B)
=
13.3*10
A
−ε
ηB VA0.71
Do(B)
= 8.93*10 −8
A
 PB 
P 
 A
0.6
J.Chem.Eng.Data 10(1965)348
∆Hi = molar heat of vaporization at the
normal boiling point
J.Chem.Ed. 47(1970)261-270
nSE(r A) = Stokes-Einstein number
J.Chem.Eng.Data 20(1)(1975)105
P i = parachor
Can.J.Chem.Eng. 60(1982)295
(1) normal paraffin solutions
(ε = 10.2/VA – 0.791)
(1)
DoA( w ) = 1.25*10 −8 ( VA−0.19 − 0.292 )
AIChE Journal 1(1955)264
Φ B = association factor of solvent B
M B = molar mass of solvent B
VA = molar volume of solute A
J.Chem.Eng.Data 8(1963)198
∆Li = specific heat of vaporization at the
normal boiling point
T1.47
(2)
η−wε
T1.29 1 PB0.5
(3)
η0.92
VB0.23 PA0.42
B
g) L.Hao and D.G.Leaist
27.8*10−5
o(x)
DA =
VA0.653
h) Bosma J.C. and Wesslingh J.A.
Do(B)
= 1.55*10 −8
A
(2) solutes in aqueous solutions
(ε = 9.58/VA – 1.12)
(3) nonaqueous ( nonelectrolyte) solutions
J.Chem.Eng.Data 41(1996)210
(x) = solvent: carbon tetrachloride
Trans.Inst.Chem.Eng. 77(1999)325
cited by Kooijman (j) (size ratio effect; “Estimation of
diffusion coefficients in dilute liquid mixtures”)
i) R.Niesner and A.Heintz
Dos ( w ) = 7.4*10 −12
T
ηw
j) H.A.Kooijman
Do(B)
= A 0 [1 − φ A ]
A
set
A0 AA
set 1: 2.50 0
set 2 3.53 1
set 3 1.58 1
Φw Mw
Vs0.6
J.Chem.Eng.Data 45(2000)1121
w=water Φ w=1.61
Ind.Eng.Chem.Res. 41(2002)3326
(SE) based on R(volume) and Q (surface area)
[1 − φ B ] θAABR Do(B)
A
UNIQUAC parameters
AB AR
A0 = Stokes-Einstein number
0
0
AA, AB = nonroundness corrections
1
0
AR = solute/solvent size ratio
1/3
1
AA
AB
E.O.T. - 2004 - FI - UBA
contener la ec.(3.41) (ver también (3.23)) magnitudes cinéticos (o de transporte),
es evidente que para de…nir completamente D id hace falta también especi…car una
idealidad de transporte (o de difusión).
Para de…nir una idealidad de este tipo corresponde tener en cuenta que estas
mezclas presentan dos valores limites correspondientes a ambos extremos del rango
de composición ya señalados antes (ver ec.(1.23)), o sea,
1(1)
D2
1(2)
= lim D ( D(x) ) lim D = D1
x2!0
x1!0
y para ambos límites valen expresiones tipo (3.29). Entonces se tiene
µ
¶
w B22
D1(1)
=
lim
D
=
RT
= RT 1 B±22 (a)
2
x2!0
c1 V 1 c 2!0
µ
¶
1(2)
w B11
D1
= lim D = RT
= RT 2 B±11 (b)
x1!0
c2 V 2 c 1!0
(3.42)
(3.43)
±
siendo j Bii
la movilidad del soluto i a dilución in…nita en el medio j. Sobre esta
base, y con consideraciones no muy convincentes, se propuesto una forma muy simple
conocida como fórmula de Hartley-Crank:(1949):
1(1)
DH C (x) = D2
1(2)
x1 + D1
x2
(Hartley ¡ Crank)
(3.44)
La ec.(3.44) tiene la misma forma ya propuesta por Meyer (1899) (ver ec.(2.32)) para
interdifusión en gases y por Darken (1948) para interdifusión en sólidos (metalurgia).
La relación (3.44) supone que el coe…ciente de interdifusión D varía en forma lineal
con la fracción molar, aunque ya se ha visto que, por argumentos de la Teoría Cinética
de los Gases, para mezclas gaseosas binarias D es independiente de la composición
(ver ec.(2.33)).
La fórmula de Hartley-Crank se puede analizar de la siguiente manera mediante los
argumentos desarrollados aquí. Se puede demostrar (ver sección siguiente, ec.(3.84))
que las movilidades difusionales w Bii en el SR de volumen …jo (w ´ c1 V 1 v1 + c2 V2 v 2 )
están relacionadas con las movilidades u Bii en el SR molar (u ´ x1 v 1 + x 2 v2 ) simplemente por
w B22
u B22
w B11
u B11
=
;
=
(3.45)
(c1 V 1 )2
x 21
(c2 V 2 )2
x 22
Sustituyendo estas relaciones en (3.41) queda
id
D (x) =
µ
u B22 (x)
x1
¶ id
RT =
µ
u B11 (x)
x2
¶id
RT
(3.46)
o sea, vale
D id (x) = RT B id (x)
(3.47)
donde B(x) es genéricamente el término cinético de la interdifusión, el cual para casos
ideales está de…nido por
id
B (x) ´
µ
u B22 (x)
x1
¶ id
36
=
µ
u B11 (x)
x2
¶ id
(3.48)
(Recuérdese que en (3.47) el término termodinámico es simplemente RT).
Obsérvese que por (3.48) las dos movilidades u Bii (i=1,2) no son independientes.
Por su parte, estas movilidades difusionales molares u Bii varían entre los siguientes
límites:
x2 !0
lim
(u!vj )
RT
u Bii
1(j)
= RT j Bii
1(j)
= Di
y
xi!1
lim
(u !v i)
RT
u Bii
=0
(3.49)
( u Bii se anula en xi = 1 pues entonces u = vi y i Bii ´ 0, ya que la movilidad de
la especie i medida respecto de sí misma es idénticaamente nula). Por lo tanto, aún
las movilidades ideales dependen de la composición y la más simple dependencia que
puede plantearse para movilidades difusionales molares ‘ideales’ es una relación lineal
según
1(j)
id
RTu Bii
(x) = Di
(1 ¡ xi )
(i = 1; 2)
(3.50)
Esta relación cumple con (3.49) y debe cumplir además con (3.48). Entonces surge
inmediatamente la siguiente restricción para este comportamiento ideal:.
1(1)¡id
D2
1(2) ¡id
(3.51)
= D1
Sustituyendo (3.51) en (3.44) queda
Did = cons tan te 6= f (x)
(3.52)
Asi, el coe…ciente de interdifusión D de las mezclas ‘ideales’ es independiente de la
composición, tal como se observa para mezclas gaseosas ideales (ver fórmula de StefanMaxwell), y las movilidades difusionales ‘ideales’ varían linealmente con la fracción
molar.
Para fases condensadas es interesante analizar la condición (3.51) en términos de la
ley (3.35) de Einstein-Stokes.: Para que se pueda cumplir (3.51) ambos componentes
(solventes) deben presentar igual tamaño molecular e igual viscosidad, una condición
muy severa, o al menos que el producto (r £ ´) sea el mismo para ambos solventes,
una condición también muy exigente. Por el contrario, es lógico pensar que distintos
tamaños y viscosidades determinen comportamientos no-ideales para las mezclas (ver
ejemplos dados en la sección 1.3), y, por lo tanto, debe concluirse que la fórmula (3.44)
de Hartley-Crank no debe considerarse una fórmula ideal, sino más bien una primera
desviación simple de la idealidad del transporte difusional dada por (3.50)-(3.51) (ver
sección siguiente).
Experimentalmente se encuentra que ni siquiera (3.44) no se cumple para sistemas
condensados termodinámicamente ideales, aunque se la utiliza cuando no hay otra
información disponible. Así se han propuesto algumas modi…caciones empíricas a
(3.44). Sobre la base de la ley de Stokes se ha propuesto lo siguiente:
1(1)
´ Did = ´ 1 D2
1(2)
x1 + ´ 2 D1
x2
(3.53)
(aproximación de Gordon ) donde ´ es la viscosidad de la mezcla y ´ 1 y ´ 2 las de los
líquidos puros. Otra alternativa es reemplazar en (3.44) las fracciones molares por
fracciones de volumen (xi ! Ái = ci Vi² ) y se tiene
1(1)
Did = D2
1(2)
Á1 + D1
37
Á2
(3.54)
También se ha sugerido como alternativas promedios geométricos (ec.de Vignes) como
³
´ x1 ³
´ x2
1(1)
1( 2)
D id = D2
D1
³
´Á 1 ³
´Á2
1(1)
1(2)
y=o D id = D2
D1
(3.55)
Todas estas propuestas de idealidad de transporte presuponen que D se puede
expresar en función directa de las propiedades de cada componente, en este caso, su
movilidad a dilución in…nita en el otro componente. Esto ultimo es característica
esencial de la interdifusión, ya que D es una propiedad del sistema, es decir, de ambos
componentes en común.
Finalmente, si todas estas suposiciones para las idealidades de ambos tipos no
se cumplen se debe emplear la formulación general,(3.22), cuyas caracteristicas se
discuten en la sección siguiente.
3.3.3. Sistemas reales.
Para sistemas binarios reales se debe aplicar la fórmual general (3.22), que, escrita
para ambos componentes, es
D=
w B22
w B11
( c)
[c2¹22 ] =
c1 V1
(c)
[c1 ¹11 ]
c2 V2
(3.56)
Se ha analizado anteriormente aspectos idealizados y para sistemas reales es conveniente dar a esta ecuación formas más prácticas. Esto signi…ca trabajar tanto sobre
los aspectos cinéticos (movilidades) como sobre los aspectos termdinámicos (factores
termodinámicos de la difusión).
Cambio de factor termodinámico. La variable de concentración molar c2 no es
una variable de concentración muy adecuada ya que varía con T y P. Es conveniente
cambiarla por la molalidad m 2 que no presenta ese inconveniente. Entonces se tiene:
·
¸
·
¸
·
¸
·
¸
@¹2
@¹2
@m 2
@m2
(c)
( m)
¹22 ´
=
=
¹
(3.57)
@c2 T ;P
@m 2 T ;P @c2 T ;P
@c2 T ;P 22
donde
(m)
¹22
·
@¹2
´
@m 2
¸
(3.58)
T ;P
y, por lo tanto,
(c)
c2 ¹22
c2
=[
m2
·
@m2
@c2
¸
(m)
] [m2 ¹22 ] =
T ;P
1
( m)
[m 2 ¹22 ]
c1 V1
(3.59)
donde hemos usado para [@m 2 =@c2 ]T ;P la relación dada en el Apéndice I. La expresión
(c)
(m)
(3.59) da la relación entre [c2 ¹22 ] y [m 2 ¹22 ], el factor termodinámico de la difusión
en la escala molal.
Por su parte, para mezclas es conveniente traba jar el FTD en la escala racional de
fracciones molares. Adaptar el FTD a la escala de fracción molar x 2 se puede efectúar
partiendo del FDT molal. Se obtiene:
·
¸
·
¸
@¹2
@x 2
@¹2
(m)
(x)
(x)
m 2 ¹22 = m 2
= x 1 [x2 ¹22 ] con ¹22 ´
(3.60)
@x 2 T ; P @m 2
@x 2 T ;P
38
donde se ha usado para @x 2 =@m 2 la relación dada en el Apéndice I.
Por lo tanto se tienen tres alternativas para el FTD:
(c)
(m)
(x)
(3.61)
(c1V 1 ) c2 ¹22 = [m 2 ¹22 ] = x1 [x 2 ¹22 ]
Los FTD están directamente relacionados con la variación con la concentración
de los correspondientes coe…cientes de actividad (Ver Apéndice I I) ya que aquellos
están de…nidos como derivadas del potencial químico respecto de la concentración.
Explicitamente vale en las distintas escalas:
·
¸
@ ln y 2 )
(c)
(c)
(c)
c2 ¹22 = RT ¡2
donde ¡2 ´ 1 +
(3.62)
@ ln c2 T ;P
·
¸
@ ln °2 )
(m)
(m)
(m)
m 2 ¹22
= RT ¡2
donde ¡2 ´ 1 +
(3.63)
@ ln m 2 T ;P
·
¸
@ ln f2 )
(x)
(x)
(x)
x2 ¹22 = ¡RT 2
donde ¡ 2 ´ 1 +
(escala Raoult)
(3.64)
@ ln x 2 T ;P
·
¸
@ ln f20 )
(x)
(x)
(x)
x2 ¹22 = RT ¡2
donde ¡ 2 ´ 1 +
(escala Henry)
(3.65)
@ ln x 2 T ;P
siendo y2; ° 2 , f2 y f02 los coe…cientes de actividad del componente 2 en las distintas
escalas (ver Apéndice II). Las funciones ¡ señalan que los FTD dependen directamente (y solamente) de las variaciones de los coe…cientes con la concentración. Por
la normalización de estos coe…cientes de actividad valen los siguientes límites para los
FTD:
(c)
lim c2 ¹22
c 2!0
( m)
lim m 2 ¹22
m2!0
(x)
lim x2 ¹22
x2!1
(x)
lim x2 ¹22
x2!0
=
RT
ya que
=
RT
ya que
=
RT
ya que
=
RT
ya que
(c)
(3.66)
lim ¡ 2 = 1
c 2!0
(m)
lim ¡ 2
c 2!0
(x)
(escala Raoult)
(3.68)
(x)
(escala Henry)
(3.69)
lim ¡ 2 = 1
c 2!1
lim ¡ 2 = 1
c 2!0
(3.67)
=1
o sea, el valor límite de los FTD es siempre RT.
En el caso de la escala racional las expresiones son simétricas para ambos componentes:
( x)
(x)
(x)
(x)
x 2 ¹22 = x 1 ¹11 y ¡2 = ¡1
(3.70)
como se puede veri…car fácilmente. Estas funciones tienen la peculiaridad de tener
los dos límites unitarios ya señalados:
·
¸
·
¸
@ ln f2
@ ln f 20
(x)
(x)
(x)
1 = lim ¡ 2 ( ¡ 2 ´ 1 +
=1+
) lim ¡ 2 = 1 (3.71)
x2!1
@ ln x 2 T ;P
@ ln x2 T ;P
x2!0
|
{z
}
|
{z
}
escala de Rao ult
escala de H enr y
ya que los coe…cientes de actividad de Raoult y de Henry tienden ambos a valores
constantes (interconvertibles) en ambos extremos del rango de composición.
Estas relaciones se deben introducir tanto en (3.22) como en (3.56). Para difusión
de solutos se obtiene:
"
#
·
¸
w B 22
(c)
w B22
(m)
D=
[c2 ¹22 ] =
(solutos)
(3.72)
2 [m 2 ¹22 ]
c1 V1
(c1 V 1 )
39
ya que la escala molal es la más práctica para solutos. En cambio para mezclas de
solventes, en las cuales ambos componentes tienen trato equivalente, la escala racional
es la más adecuada y se deriva:
D=
"
w B22
2
(c1 V 1 )
x1
#
(x)
[x 2 ¹22 ]
=
"
w B11
2
(c2 V 2 )
#
(x)
x 2 [x 1 ¹11 ]
(3.73)
(mezclas)
Se observa que la introducción de distintas formas del FTD modi…ca el término de
movilidades. Es conveniente analizar si estos términos responden a movilidades expresadas en sistemas de referencia (SR) más adecuados.
Cambio de movilidad. La ecuación (3.72) se puede simpli…car transformando la
movilidad w B22 del SR de volumen …jo a la del SR de solvente …jo 1 B22 . La relación
de transformación se obtiene mediante la relación entre los ‡ujos w J 2 y 1 J 2 :
wJ 2
=
=
=
c2 (v 2 ¡ w) = c2 (v2 ¡ (c1 V 1 v1 + c2 V 2 v2 ) =
c2 (v 2 ¡ v 1 + v1 (1 ¡ c1 V 1 ) ¡ c2 V2 v 2 ) =
(1 ¡ c2 V 2 ) c2 (v 2 ¡ v 1 ) = c1 V 1 1 J 2
)
w J2
= c1 V1 1 J2 , (3.74)
y con esta relación se obtiene las siguientes conecciones entre los CF y las respectivas
movilidades:
wJ 2
=¡
w L22
grad ¹2
= c1 V 1 1 J2 = ¡(c1 V 1 ) 1 L22 grad ¹2
c1 V 1
(3.75)
Por lo tanto
w L22
= (c1 V1 )2 1 L22
y
w B22
= (c1 V 1 )2 1 B22
donde
1 B 22
´
1 L22
c2
(3.76)
y de (3.72) se obtiene
(m)
(m)
D = [1 B22 ] [m 2 ¹22 ] = RT 1 B22 ¡2
(solutos)
(3.77)
donde se ha utilizado también (3.63). La nueva expresión en la escala molal es llamativamente simple.
Por su parte, para discutir las características de la difusión en mezclas binarias
completamente miscibles, ya sean líquidas o gaseosas, para las cuales la variable (termodinámica) natural es la fracción molar, para los fenómenos de transporte en estos
sistemas el sistema de referencia natural es el SR molar, o sea,
u = x1 v 1 + x 2 v2
(3.78)
Para introducir este SR se opera de la misma forma que antes. Partiendo de la
de…nición de la velocidad media molar u se obtiene (x 1 + x 2 = 1)
u
´
)
x 1 v1 + x 2 v2 = v 2 ¡ x1 (v 2 ¡ v 1)
v 2 ¡ u = x 1 (v 2 ¡ v1 )
(3.79)
Entonces la relación entre ‡ujos es
u J2
= c2 (v 2 ¡ u) = x 1 c2 (v 2 ¡ v 1) = x 1 1 J 2
40
(3.80)
y para la relación entre las EF en ambos SR (ver Parte I, sección 4 y 5) se obtiene:
x 1 1 J2
= x 1 [1 L22 (¡gradT ;P ¹2 )] =
u J2
=
uL 22
[(¡gradT ;P ¹2 ) ¡ (¡gradT ;P ¹1 )]
(3.81)
Recordando la ec. de Gibbs-Duhem (x1 dT ;P ¹1 +x 2 dT ;P ¹2 = 0) se deduce …nalmente:
u J2
= x 1 [1 L22 (¡gradT ;P ¹2 )] =
u L22
[
¡gradT ;P ¹2
]
x1
(3.82)
y de aqui:
u L22
= x21 1 L22
y
u B22
= x21 1 B22
donde
u B22
´
u L22
c2
Reemplazando en (3.73), teniendo en cuenta (3.76), se encuentra:
·
¸
·
¸
u B22
(x)
u B 22
(x)
D =
[x 2¹ 22 ] =
RT ¡ 2
x1
x1
·
¸
·
¸
u B11
(x)
u B 11
(x)
=
[x 1¹ 11 ] =
RT ¡ 1
(mezclas)
x2
x2
(3.83)
(3.84)
donde la expresión para el componente 1 se ha escrito por simetría, y además se ha
utilizado también las relaciones (3.64), (3.65) y (3.70). Además
(3.85)
x 2 u B22 = x 1 u B11
(verifíquese).
Las fórmulas (3.56), (3.77) y (3.84) señalan que a cada SR le corresponde un FTD
adecuado. Resumiendo se tienen las siguientes expresiones generales y equivalentes
para D para un sistema binario:
D
w B22
=
(c)
w B11
( c)
[c1¹11 ]
c1 V1
c2 V2
u B22
(x)
u B11
(x)
[x2 ¹22 ] =
[x1 ¹11 ]
x1
x2
=
=
1 B22
[c2 ¹22 ] =
(m)
[m 2 ¹22 ] =
2 B11
(a)
(b)
(m)
[m1 ¹11 ]
(c)
(3.86)
donde la última expresión también se ha escrito por simetría.
Las expresiones generales (3.86) conducen a la siguiente relación límite, respetando
los límites de las magnitudes involucradas que ya se han visto antes,:
1(1)
limc2!0 D = D2
= RT
1(1)
w B22
= RT
1(1)
u B22
1(1)
= RT 1 B22
(3.87)
convalidando (3.34). Se observa que las movilidades fenomenológicas en los distintos
SR son iguales en el límite de dilución in…nita. La expresión dada es generalizable
para dilución in…nita en cualquier medio soporte S y para cualquier especie K (usando
ahora el índice o para el solvente):
1( S)
lim cK!0 D = DK
41
1(S)
= RT o BK K
:
(3.88)
Es evidente que la dependencia con la composición de estos FTD determina en
buena parte el comportamiento del coe…ciente de interdifusión D. A mayor desviación
de la idealidad se observa un comportamiento más complejo, aunque debe diferenciar
-se la idealidad de equilibrio (coe…cientes de actividad unitarios) de la idealidad de
transporte (movilidades lineales en fracciones molares).
Concordantemente para mezclas condensadas vale para ambos extremos:
1(1)
1( 1)
RT 1 B22 = D2
|
{z
u!v1
1(2)
= lim D ( D(x 2 ) ) lim D = D1
x2!1
} x2!0
|
1(2)
= RT 2 B11
{z
u!v2
(3.89)
}
y ambos valores extremos son …nitos y distintos y corresponden al componente en
situación de vestigio.
En este contexto es adecuado volver a analizar la fórmula (3.44) de Hartley-Crank.
Considerando las fórmulas (3.84) reescritas de la siguiente manera (recordar (3.70))
·
¸
·
¸
D(x)
u B22 (x)
u B11 (x)
= RT
= RT
(3.90)
(x )
x1
x2
¡ (x)
1
e introduciendo el término cinético genérico B(x) de…nido ya en (3.48),
B(x) ´
u B22 (x)
x1
u B11 (x)
=
x2
(3.91)
;
se puede formular (3.90) como
D(x)
(x)
¡1 (x)
= RT B(x) (x1 + x2 ) = RT
u B22 (x)
+ RT
u B11 (x)
(3.92)
Esta relación señala que RT B(x); la parte cinética de coe…ciente de interdifusión
D, es decir, D corregido por el FTD racional, puede tomarse como la suma de las
movilidades racionales de ambos componentes.
Se observa que, por una parte, de (3.92) con (3.50) y (3.48) se obtiene las relaciones
ideales (3.51) y (3.52). Por otra parte, para mezclas reales vale (3.89) y no (3.51) y,
por lo tanto, debe ampliarse la propuesta ideal (3.50) para mezclas reales. Toda
ampliación debe preservar los límites (3.49) y (3.85) y la más simple es agregar un
término mixto en x1 x 2 ; o sea,
RTu B22 (x)
RTu B11 (x)
1( 1)
=
D2
=
1( 2)
D1
x2
x1 + d2 x1 x 2
(3.93)
+ d1 x1 x 2
Recordando (3.85) (o (3.91)) se deduce enseguida que las constantes d1 y d2 están
relacionadas según
1(1)
1(2)
d2 = D2
¡ D1
(´ ¢D1 ) = ¡d1
(3.94)
y entonces (3.93) se pueden reescribir como
RT u B22 (x)
= x 1 fD2
1( 1)
x1 + D1
1( 2)
RT u B11 (x)
= x 2 fD1
1( 2)
x2 + D2
1( 1)
42
1(1)
x2 g = x1 D2
1(2)
x1 g = x2 D1
¡ ¢D1 .x 1 x2
+ ¢D1 ,x 1 x2
(3.95)
Finalmente sustituyendo estas expresiones en (3.92) se obtiene
D(x)
(x)
¡ 1 (x)
1(1)
= RT B(x)HC = DH C (x) = D2
1(2)
x 1 + D1
x2
(3.96)
La ec.(3.96) señala que la fórmula de Hartley-Crank vale para mezclas condensadas
levemente reales ( mezclas regulares), para las cuales las movilidades difusionales presentan, según (3.93), una leve desviación de la idealidad (3.50) de difusión. (Obsérvese
que con d2 =d 1 =0=¢D1 se obtiene idealidad.).
A nivel termodinámico la más leve desviación de la idealidad (3.38) está dada por
las mezclas también denominadas regulares. Para éstas los coe…cientes de actividad
racionales están dadas simplemente por
RT ln f 2 = Ax 21 ;
RT ln f1 = Ax22
(A 6 2RT )
(3.97)
(A es la constante de Porter) y el FDT vale entonces (verifíquese)
(x)
(x)
¡2 = ¡1 = 1 ¡
2 A x1 x2
RT
(mezclas regulares)
(3.98)
Combinando (3.96) y (3.98) se deriva para D en estas mezclas:
1(1)
D(x) = [D2
1(2)
x1 + D1
x2 ][1 ¡ 2(A=RT )x 1 x2 ]
(3.99)
la expresión real más simple para el coe…ciente de interdifusión D. Experimentalmente
se encuentra que prácticamente ningún sistema cumple con esta relación, es decir, que
las desviaciones de los sistemas reales son más fuertes que lo predicho por (3.99).
Finalmente corresponde señalar que hay todavía otra propuesta o alternativa para
interpretar el coe…ciente de interdifusión D vía una ecuación tipo Hartley-Crank. La
misma trata de relacionar D con los coe…cientes de intradifusión D¤i (i=1,2) de ambos
componentes según
¤
¤
D(x)=¡(x)
1 (x) = RT B(x) = D2 (x) x 1 + D1 (x) x2
(3.100)
una relación que tampoco ha encontrado mucha aplicación, en parte porque requiere
conocer datos de los tres coe…cientes de difusión involucrados, lo cual no es siempre
el caso. Ya que todavía no se ha discutido en los presentes escritos el fenómeno de
intradifusión se deja el análisis más detallado de (3.100) para el capítulo correspondiente.
3.3.4. Ejemplos experimentales.
a) Sistema benceno-ciclohexano. En las láminas adjuntas se analiza el coe…ciente de interdifusión D del sistema benceno-ciclohexano tanto en la escala racional,
en función de las ecs.(3.84), como en la escala molal, en función de la ec.(3.77) y/o
(3.86c). Se observa que D no es lineal en la composición, o sea, que no vale la ec. de
Hartley-Crank.
43
Escala racional. En la primera lámina en su linea superior se dada el FTD en la
escala racional (fracción molar), que es simétrico (ver ec.(3.64)) y veri…ca los límites
dados por (3.68). Los coe…cientes de actividad de los componentes responden bien
a las ecs. de van Laar. En la …gura siguiente se dan las movilidades de ambos
componentes en el SR molar dadas por (3.90), que están relacionadas según (3.85) asi
como el término cinético genérico dado por (3.92). Los límites correspondientes (ver
(3.49)) se cumplen tanto a dilución in…nita (ver ecs.(3.89)) como para xi ! 1: En este
último caso u ! v i y el límite de uB ii es cero, ya que esta movilidad del componente
i termina midiéndose respecto su propia velocidad, y entonces esta movilidad es nula
por de…nición.
En la …gura también está representada la fórmula lineal (3.44) de Hartley-Crank
y las movilidades correspondientes dadas por las ecs.(3.95) (lineas de guiones). Se
observa que no representan los datos experimentales.
En la segunda láimina se dan más detalles. Se repiten las dos primeras …guras. Además se han analizado las movilidades difusionales racionales ampliando
las ecs.(3.95) de la siguiente manera, agregando otro término de tipo x 1 x2 , ahora de
naturaleza empírica,
RT
u B22 (x)
=
RT
u B11 (x)
=
x1 DH C + g(x):x 21 x 2 = D21(1):x 1 ¡ ¢D1 .x 1 x2 + g(x):x 21 x2
1(2)
x2 DH C + g(x):x 1 x 22 = D1
:x 2 + ¢D1 .x 1 x2 + g(x):x 1 x22
(3.101)
donde la función g(x) representa la desviación a la ec.(3.96), esto es,
D(x)
(x)
¡ 1 (x)
= RT B(x) = RT B(x) HC + g(x):x1 x 2
(3.102)
Experimentalmente la función g(x) se obtiene directamente según
g(x) =
D=¡(x) ¡ D HC
x1 x 2
(3.103)
Esta función g(x) representa, como es uso en general en Termodinámica, una función
de exceso sobre cierta función tomada como referencia (o ideal), es este caso, D HC :
La función exceso g(x) está representada en la tercera …gura. En el presente caso
se observa que g(x) se puede considerar constante (g = 1:24 £ 10 ¡5 ) y responde a las
siguientes relaciones:
g
con
1(1)
D2
=
=
1(2)
0:66 £ D1
2:105 £ 10
¡5
1( 1)
(3.104)
= 0:59 £ D2
2
cm =s;
1(2)
D1
= 1:882 £ 10
¡5
2
cm =s:
Introduciendo estas condiciones en (3.101) queda, recordando (3.96),
1(1)
RT
u B22(x)
= x 1 [DHC + g:x 1 x2 ] = x 1 [D2
¡ (¢D 1 ¡ g:x1 ):x 2 ]
RT
u B11(x)
= x 2 [DHC + g:x 1 x2 ] = x 2 [D1(2)
+ (¢D 1 + g:x2 ):x 1 ] (3.105)
1
o sea, la constante g determina las desviaciones de las movilidades respecto del comportamiento de referencia de Hartley-Crank.
44
Interdiffusion in Benzene(1)-cycloHexane(2)
Diffusion coefficients
Rational thermod. factor
1,0
D1* (Bz)
RT B(x)
D (cm 2 s-1) *10 5
2,2
D 2* ( cHx)
2,0
1,8
Dv(Bz-cHx)
1,6
Γ(x) (ratonal thermod.factor)
2,4
0,9
Bz(1)
cHx(2)
0,8
0,7
(i=1,2)
1,4
0,0
0,2
0,4
0,6
0,8
0,6
0,0
1,0
0,2
0,4
0,6
0,8
1,0
x 1(Benzene)
x 1(Benzene)
g(x)
Rational interdiffusional mobilities
2,0
2,5
2,0
g(x)*105
RT.uBii *10
5
1,5
1,0
1,5
cHx(2)
Bz(1)
1,0
0,5
(i=1,2)
0,5
0,0
0,2
0,4
0,6
x 1 (benzene)
0,8
1,0
0,0
0,0
0,2
0,4
0,6
0,8
x 1(Benzene)
eot (2003)
1,0
D (cm^2 s-1) *10^5
1.4
0.0
1.6
1.8
2.0
2.2
2.4
0.2
0.6
0.8
*(
D2 cHx)
*( Bz)
x1(Benceno)
0.4
D v(Bz-cHx)
D1
1.0
x)
Diffusion coefficients
(racional thermod.
(
Γi
m)
(molal thermod. fa
(
Γi
0.0
0.0
0.2
0.4
0.6
0.8
1.0
0.6
0.0
0.7
0.8
0.9
1.0
0.6
x1(Benceno)
0.4
(i=1,2)
0.8
cHx(2)
0.2
x1(Benceno)
0.8
cHx(2)
0.6
(i=1,2)
0.4
Bz(1)
Molal thermod. factors
0.2
Bz(1)
Racional thermod. factors
1.0
1.0
RT.ubii *10^5
RT.jbii *10^5
10
cHx(2)
0.2
0.4
0.6
x1(Benceno)
(i=1,2; j=2,1)
0.0
-2
10 -1
10 0
10 1
10 2
10 3
10 4
0.6
x1(Benceno)
0.4
(i=1,2)
0.8
Bz(1)
0.8
Bz(1)
Interdiffusional mobilities
0.2
cHx(2)
-0.5
0.0
0.0
0.5
1.0
1.5
2.0
2.5
3.0
1.0
1.0
Racional interdiffusional mobilities
Utilizando estos valores se han calculado las movilidades según (3.101). Estas
movilidades representan bien los valores experimentales (lineas llenas) según se observa en la cuarta …gura, donde también está dado el término genérico RT.B(x) (ec
(3.92)). También reproduce bien el coe…ciente D (linea llena) en la …gura principal,
calculado mediante (3.90) con (3.101) y el FTD dado en la linea superior.
El comportamiento de D de éste sistema es relativamente simple; las movilidades
difusionales no se apartan mucho de una linealidad. En parte se podía esperar este
resultado ya que ambos componentes son químicamente bastante semejantes. Por su
parte, esto no es el caso para el caso agua-etanol, que se analiza en la lámina siguiente
(ver más aba jo).
Escala molal. En la linea inferior de la primera lámina de éste sistema se analiza
los FDT en la escala molal (ver ec.(3.63)). Su dependencia con la composición es
mucho más marcada, variando según
(m) (3:71)
RT = lim mi ¹ii
(m)
( mi ¹ii
xi!0
(m)
) lim m i¹ii
xi!1
= 0;
(3.106)
donde para el límite x i ! 1 desaparece el otro componente que ‘hace’ de solvente y
entonces limxi !1 m i = 1:
En la …gura siguiente se dan en grá…co semi-logarítmico las movilidades según
(3.77) en el SR de Hittorf, o sea, de especie, siendo la especie de referencia el otro
componente de la mezcla. Estas movilidades se obtienen directamente por el cociente
(m)
D=[m i¹ii ] según (3.86). Por otra parte, estas movilidades están relacionadas con
las movilidades racionales según (3.81), a saber,
1 B22
=
u B22
x 21
B(x)
x1
=
y
2 B11
=
u B11
x 22
=
B(x)
x2
(3.107)
(usando también (3.91)) y presentan una dependencia con la composición completamente distinta. Introduciendo aquí las ecs.(3.101) queda más explictamente
RT 1 B22
=
RT 2 B11
=
DH C + g:x 1 x2
x2
1(1)
1(2)
= D2
+ (D1
+ g:x 1 )
x1
x1
DH C + g:x 1 x2
x1
1(2)
1(1)
= D1
+ (D2
+ g:x 2 )
x2
x2
(3.108)
donde se ha utilizado (3.96). Se oberva que la dependencia con la composicíón es
ahora hipergólica y estas movilidades crecen mardamente con la composición. Los
límites correspondientes a dilución in…nita son …nitos (ver ec.(3.87)); en cambio en
el límite x i ! 1 estas movilidades divergen a +1 ya que desaparece la especie de
referencia. Este valor límite es también consistente con el valor límite del FDT en esa
situación (ver (3.106)) ya que
lim D = f inito =
xi!1
lim
[mi ¹(m)
] £ [ j Bii ] = 0 £ 1
| {zii }
|{z}
xi!1(xj !0)
!0
(= D1(i)
):
j
(3.109)
!+1
b) Sistema agua-etanol. En la lámina siguiente se analiza el sistema agua-etanol.
En el grá…co de la parte superior izquierda se da el coe…ciente de interdifusión correspondiente, el cual, aunque sus valores límites son bastante parecidos, se aparta
47
Water(1)-Ethanol(2)
1,2
rationa thermod. factor
Dv (cm2 s-1)
1,5
1,0
0,5
o
25 C
0,0
0,0
0,2
0,4
0,6
0,8
1,0
0,8
0,6
0,4
0,0
0,0
1,0
o
40 C
0,2
0,2
x2 (ethanol)
0,4
0,6
0,8
1,0
x2 (ethanol)
1,5
4
0
1,0
g(x)*10^5
RT uB *10^5
2
0,5
-2
-4
-6
-8
0,0
0,0
0,2
0,4
0,6
0,8
-10
0,0
1,0
glin=-2.91+4.52*x2
gprb=-5.59+17.4*x2-11.9*x2
0,2
x2 (ethanol)
0,4
0,6
2
0,8
1,0
x2 (ethanol)
1,5
Pv, P1, P2 (mmHg)
RT uBii (i=1,2)
120
1,0
0,5
0,0
0,0
0,2
0,4
0,6
x2 (ethanol)
0,8
1,0
90
60
40 oC
30
0
0,0
0,2
0,4
0,6
0,8
x2 (ethanol)
eot (2004)
1,0
marcadamente de la linealidad en las mezclas. En la parte superior derecha están
gra…cados los coe…cientes de actividad de ambos componentes, obtenidos de datos de
equilibrio líquido-vapor. En estos datos se ha calculado el FTD, representado en la
parte media a la izquierda. Por otra parte en la parte media derecha está gra…cado
la función difusional de exceso g(x) (calculada según (3.103)), función que es ahora
parabólica en la composición. Finalmente en la parte inferior se ha gra…cado a la
izquierda el término cinético genérico RTB(x), tanto por sus valores experimentales
como por la curva calculada con la función g(x), y en la parte derecha las movilidades
difusionales racionales de ambos componentes. Se observa que estas movilidades dependen marcada y peculiarmente con la composición.
Todas estas características, típicas para la descripción de la interdifusión dada
por la TPI, surgen de la relación general (3.23) que señala a D como una magnitud
compuesta:
coef. de difusión
= movilidad difusional
£ factor termodinámico
(ec:(3:23))
Al respecto debe destacarse que D es la magnitud experimentalmente determinable,
y entonces las distintas movilidades de difusión que se quieran utilizar son solamente
accesibles si se tiene además información de Termodinámica de Equilibrio, es decir,
si se conocen los factores termodinámicos FDT correspondientes. Ambas magnitudes
determinan el comportamiento de D y si se hacen modelos teóricos los mismos deben
abarcar las dos magnitudes, lo cual no ocurre en general con modelos que se encuentran en la literatura. Es más, en general se pasa por alto o se ‘olvida’ el aspecto
termodinámico de la difusión; al respecto véase la sección 2.5.1.
c) Otros sistemas. Las láminas siguientes contienen un análisis similar para los
sistemas acetona-clooformo y octano-docenao.
3.3.5. Difusión en puntos críticos.
Un caso termodinámico especial permite ilustrar la importancia e incidencia del FDT.
Se trata del comportamiento del coe…ciente de interdifusión en un punto crítico, punto
en el cual D se anula, tal como se muestra en la …gura (11) dada en la tercera
lámina de la sección 1. Este comportamiento está exclusivamente determinado por
el FDT, ya que la movilidad difusional es …nita en este punto (la agitación térmica
de las moléculas no se anula o ‘congela’ en un estado crítico). Se demuestra en
(x)
Termodinámica de Equilibrio que para un sistema binario las derivadas ¹ii (i = 1; 2)
son siempre positivas en una fase o región estable o metaestable (y por ello los FDT son
también siempre positivos para estas fases) y son negativas para fases inestables. Por
lo tanto, en el límite de estabilidad (linea spinodal) entre fases estables e inestables
estas derivadas se anulan, y el punto crítico de miscibilidad se encuentra sobre la
linea de estabilidad. En consecuencia los FDT son nulos en el límite de estabilidad
y particularmente en los puntos críticos. Esta consideración termodinámica explica
fácilmente el comportamiento de D en estos puntos, tal como lo muestra la …gura
mencionada. En cambio, sin recurrir a estos argumentos tanto de equilibrio como de
no-equilibrio dicho comportamiento sería muy difícil de explicar. Y todo ello habla a
favor de la linea general de descripción de la difusión dada aquí.
49
Chloroform(1)-Acetone(2)
4,5
2,0
rationa thermod. factor
Dv +10^5
4,0
3,5
3,0
2,5
2,0
0,0
0,2
0,4
0,6
0,8
1,5
1,0
0,5
0,0
0,0
1,0
0,2
x2 (acetone)
3,0
glin=-2.5
-2.5*(x1-x2)
2,5
-2.5*(x1-x2)
-0.7*(x1-x2)^2
g(x)*10^5
RT uB *10^5
3,5
gprb=-2.3
0,2
0,4
0,6
0,8
1,0
3
2
1
0
-1
-2
-3
-4
-5
-6
-7
0,0
0,2
x2 (acetone)
1,0
0,4
0,6
0,8
1,0
250
3,0
Pv, P1, P2 (mmHg)
RT uBii *10^5 (i=1,2)
0,8
x2 (acetone)
4,0
2,0
1,0
0,0
0,0
0,6
x2 (acetone)
4,0
2,0
0,0
0,4
0,2
0,4
0,6
x2 (acetone)
0,8
1,0
200
150
25oC
100
50
0
1,0
0,8
0,6
0,4
0,2
0,0
x1 8chloroform)
eot (2004)
Octane(1)-Dodecane(2)
(molar fraction scale)
1,5
Rational therm. factor
Dv (cm^2 s^-1)
2,0
1,5
1,0
0,5
0,0
0,0
0,2
0,4
0,6
0,8
1,0
0,5
0,0
0,0
1,0
0,2
x2 (dodecane)
g(x)
1,5
1,0
0,5
0,2
0,4
0,6
0,8
1,0
0,0
1,0
0,2
0,4
0,6
0,8
1,0
0,8
1,0
x2 (dodecane)
1,2
Rational therm. activiti
2,0
1,5
RtuBii
0,8
0,2
0,1
0,0
-0,1
-0,2
-0,3
-0,4
-0,5
-0,6
x2 (dodecane)
1,0
0,5
0,0
0,0
0,6
x2 (dodecane)
2,0
0,0
0,0
0,4
0,2
0,4
0,6
x2 (dodecane)
0,8
1,0
1,0
0,8
0,6
0,4
0,2
0,0
0,0
0,2
0,4
0,6
x2 (dodecane)
eot (2004)
Octane(1)-Dodecane(2)
(volume fraction scale)
1,5
Rational therm. factor
Dv (cm^2 s^-1)
2,0
1,5
1,0
0,5
0,0
0,0
0,2
0,4
0,6
0,8
1,0
0,5
0,0
0,0
1,0
0,2
xv2 (dodecane)
g(v)
RTB(x)
1,5
1,0
0,5
0,2
0,4
0,6
0,8
1,0
0,0
1,0
0,2
0,4
0,6
0,8
1,0
0,8
1,0
xv2 (dodecane)
1,2
Rational therm. activiti
2,0
1,5
RtuBii
0,8
0,2
0,1
0,0
-0,1
-0,2
-0,3
-0,4
-0,5
-0,6
xv2 (dodecane)
1,0
0,5
0,0
0,0
0,6
xv2 (dodecane)
2,0
0,0
0,0
0,4
0,2
0,4
0,6
xv2 (dodecane)
0,8
1,0
1,0
0,8
0,6
0,4
0,2
0,0
0,0
0,2
0,4
0,6
xv2 (dodecane)
eot (2004)
3.4. Formulación de resistancia para difusión.
Como ya se ha visto en la Parte I, existe como alternativa a la formulación fenomenológica de conductancia el planteo de resistencia, planteo que es completamente
equivalente. Mediante las ecs. I-5.69-71 se pueden escribir para un sistema binario
las ecuaciones de transporte de la siguiente manera:
X2
= R21 c1 v1 + R22 c2 v2
X1
= R11 c1 v1 + R12 c2 v2
(3.110)
donde R ij (i,j=1,2) son los coe…cientes fenomenológicos de resistencia, para quienes
valen las siguientes relaciones
c1 R11 + c2 R21
=
0
c1 R21 + c2 R22
=
0
con
(3.111)
RRO
(3.112)
R12 = R21
Y estas ecs. se pueden transformar en el planteo de fricción mediante las ecs. I-5.7576. Se obtiene:
X2
X1
= F 21 (v2 ¡ v 1 )
(3.113)
= F 12 (v1 ¡ v 2 )
donde los coe…cientes de fricción Fij están dados por
F21 = ¡R21 c1
y
F 12 = ¡R12 c2
(3.114)
Es conveniente recordar que estos coe…cientes fenomenológicos son independientes del
sistema de referencia en que se formulan los ‡ujos de los componentes.
Pasando especí…camente al transporte por difusión se deben adaptar estas ecuaciones al caso y compararlas con las ecs. empíricas de Fick.
Las fuerzas correspondientes están dadas por (3.1). Para el caso binario se puede
usar directamente las expresiones tipo (3.18) para las fuerzas:
dif
=
dif
Y 2 = ¡gradT ;P ¹2 = ¡¹22 grad c2
=
Y 1 = ¡gradT ;P ¹1 = ¡¹11 grad c1 :
X2
X1
( c)
( c)
(3.115)
Sustituyendo estas expresiones en (3.113) y multiplicando la primera por c2 y la
segunda por c1 resulta:
(c)
¡c2 ¹22 grad c2
=
F21 c2 (v2 ¡ v1 )
grad c1
=
F12 c1 (v1 ¡ v2 )
(c)
¡c1 ¹11
(3.116)
En los miembros derechos de estas relaciones aparecen los ‡ujos 1 J 2 y 2 J1 ; respectivamente. Por (3.74) estos ‡ujos se pueden convertir en los ‡ujos en el SR de Fick.
Queda:
(c)
¡c2 ¹22 grad c2
= F 21
w J 2=(c 1 V 1 )
grad c1
= F 12
w J 1=(c 2 V 2 )
¡c1 ¹(c)
11
53
(3.117)
y reagrupando se deduce:
wJ 2
=
wJ 1
=
(c1 V 1 )
c2 ¹(22c) grad c2 = ¡D grad c2 ;
F 21
(c2 V 2 )
( c)
¡
c1 ¹11 grad c1 = ¡D grad c1 ;
F 12
¡
(3.118)
donde se ha introducido explícitamente las expresiones empíricas de Fick, teniendo
en cuenta a (1.20). Comparando se obtiene la expresión del coe…ciente de difusión D
en función de los coe…cientes de fricción binarios:
D =
(c1 V 1 )
(c2 V 2 )
(c)
(c)
c2 ¹22 =
c1 ¹11
F 21
F 12
(3.119)
En estas expresiones aparecen, como debía esperarse, los factores termodinámicos
de la difusión, aquí en la escala c. Como se ha visto en las secciones anteriores, estos
factores se pueden expresar en forma más práctica. Utilizando (3.59) y (3.92) se
encuentran expresiones equivalentes, y eventualmente más simples:
(m)
D
(m)
=
m 2 ¹22
m 1 ¹11
=
=
F 21
F 12
=
x 1 (x2 ¹22 )
x 2 (x 1 ¹11 )
=
F 21
F12
( x)
(a)
(x)
(3.120)
(b)
Estas expresiones para D son completamente equivalentes a las obtenidas antes
en función de movilidades. Mientras estas últimas dependen de los SR utilizados
para los ‡ujos, en las ecs. (3.119)-(3.120) aparecen siempre los mismos coe…cientes de
fricción F 21 y F 12 , ya que estos son independientes de estos sistemas. Comparando
las ecs.(3.119)-(3.120) con las ecs.(3.86) obtenidas antes se deducen las siguientes
relaciones entre ambos tipos de coe…cientes de transporte:
D
(m)
m2 ¹22
D
(m)
m1 ¹11
=
1
w B22
=
=
F21
(c1 V 1 )2
1 B22
=
uB 22
x21
(a)
=
1
w B11
=
=
F12
(c2 V 2 )2
2 B11
=
uB 11
x22
(b)
(3.121)
Es evidente nuevamente que las más simples son los factores termodinámicos en
la escala m y las movilidades en el SR de referencia de Hittorf ( de especie). Ya que
(ver ecs.(3.114) y (3.112))
F 21 =c1 = F 12 =c2
(3.122)
las relaciones (3.121) son interconvertibles (ver p.ej. (3.85)). En las …guras dadas de
movilidades sus inversas dan directamente los coe…cientes de fricción binarios.
Finalmente corresponde analizar los valores límites de F 21 y F 12 ; en analogía con
las expresiones (3.87) y (3.89). Se obtiene, respetando los límites correspondientes de
los factores termodinámicos (ecs.(3.66)-(3.69)),
1(1)
limc 2!0 D = D2
=
RT
1(1)
F 21
[= RT
1(1)
w B22
54
= RT
1(1)
u B22
1(1)
= RT 1 B22
] (3.123)
y
1(2)
limc 1!0 D = D1
=
RT
1(1)
F 12
[= RT
1(2)
w B11
= RT
1(2)
u B11
1(2)
= RT 2 B11
] (3.124)
expresiones que generalizan las ecs.(3.87) y (3.89).
Se observa que a dilución in…nita los coe…cientes de interdifusión son inversamente
proporcionales a la fricción de la especie correspondiente con las moléculas del medio.
Esta conclusión es generalizable, en analogía con (3.88), a medios compuestos:
limcK!0 D = D1(S)
= P
K
RT
1(S)
J 6=K F KJ
1( S)
[= RT o BK
K ]
(3.125)
es decir, si en el medio hay varios componentes las fricciones con cada una de ellas se
suman para determinar el coe…ciente de difusión a dilución in…nita.
Observaciones …nales. Todo lo visto señala en forma exhaustiva que la interpretación integral del coe…ciente de difusión empírico de Fick se logra mediante la
TPI. Como ya se ha dicho, el coe…ciente de interdifusión D es la magnitud experimentalmente medible, y el acceso a las movilidades difusionales para hacer un análisis
más profundo solo se logra mediante el conocimiento adicional de los FTD, magnitudes experimentales correspondientes a la Termodinámica de Equilibrio. Estos datos
no son siempre accesibles y, por lo tanto, es comprensible que en la literatura se utilice tanto la interpretación de Einstein de D, aproximación que signi…ca suponer que
FDT¼RT.
3.5. Otras expresiones de la ley de Fick.
En la literatura práctica se utilizan a menudo otras expresiones de la ley de Fick.
Todas ellas se pueden derivar de una expresión general para esta ley que se debe a de
Groot y col. (1953) , expresión que da el ‡ujo difusional en cualquier SR conservando
D como de…nido en el SR de volumen …jo. La ecuación de de Groot es la siguiente:
! Ji
= ¡D
1 ¡ !i
grad x i
(1 ¡ x i)V¹
(i=1,2)
(3.126)
donde V¹ es el volumen molar del sistema. Aplicaremos este relación a los distintos
SR.
SR de volumen …jo: ! = w
Vale
w Ji
=
)
(! i = ciV i;
ci = ni =V = xi =V¹ ) :
1 ¡ ci V i
grad x i (i = 1; 2)
(1 ¡ x i )V¹
cj Vj
grad x i
(i = 1; 2;
w Ji = ¡D
x j V¹
¡D
55
j = 2; 1)
o sea
wJ 2
V1
c2
= ¡D ¹ 2 grad x 2 = ¡D grad c2 = ¡D (c1 V 1)
grad m 2
V
m2
(a)
wJ 1
V2
c1
= ¡D ¹ 2 grad x 1 = ¡D grad c1 = ¡D (c2 V 2)
grad m 1
V
m1
(b)
(3.127)
Queda así expresada la ley original de Fick en función de gradientes de concentración
dados en las distintas variables de concentración usuales. Se han utilizado aquí las
relaciones dadas en el Apéndice I.
SR de especie …ja: 1) ! = v1 (!1 = 1)
y 2) ! = v 2
Las expresiones de los ‡ujos difusionales son ahora
(! 2 = 1) :
1 J2
= ¡D
1
c2
D
grad x2 = ¡D
grad m2 = ¡
grad c2
¹
x1 V
m2
c1 V1
(a)
2 J1
= ¡D
1
c1
D
grad x1 = ¡D
grad m1 = ¡
grad c1
x2 V¹
m1
c2 V2
(b)( 3.128)
SR molar: ! = u
Aqui tenemos
(! i = xi )
1
= ¡D ¹ grad x i
V
expresiones que suelen escribirse como
u Ji
u J1
= ¡Dm1 grad x 1
uJ2
(i = 1; 2)
= ¡Dm2 grad x 2
(3.129)
(3.130)
donde los nuevos coe…cientes se denominan difusividades molares. Se deduce inmediatamente que ambas difusividades son iguales y que su relación con D es la siguiente:
difusividad molar
1
Dm1 = Dm2 = D(x 2 ) ¹
V (x 2)
(3.131)
La dependencia con la composición de estas difusividades puede ser más compleja que
la de D. (Por estas de…niciones puede verse, p.ej., McCabe y Smith ”Unit operation
of chemical engineering” McGraw-Hill 1956, 1967)
SR baricéntrico: ! = v
(! i = ½i =½)
¹ V¹ ]
[½i=ci Mi; (½i =½)=(x iV¹ )= (ciM i )=(xi V¹ ½)= M i=(V¹ 2 ½)= M i= M
Las correspondientes expresiones de los ‡ujos difusionales son en general
v Ji
= ¡D
1 ¡ ½i=½
grad xi
(1 ¡ x i)V¹
(i = 1; 2)
(3.132)
y especí…camente
vJ1
= ¡D
½2 =½
M2
grad x 1 = ¡D ¹ ¹ grad x 1
¹
x2 V
MV
56
vJ2
M1
= ¡D ¹ ¹ grad x2 (3.133)
MV
¹ es la masa molar media del sistema.
donde M
En este SR se suele operar con los ‡ujos másicos v Ji¤ en vez de los ‡ujos molares
y se tiene
¤
vJ1
= M1 v J 1 = ¡D
Ya que v J 1¤ = ¡ v J2¤
tamente
M1 M2
grad x 1
¹ V¹
M
y
¤
vJ1
¤
v J2
M2 M 1
grad x2
¹ V¹
M
(3.134)
es usual que se escriba direc-
= M 2 v J2 = ¡D
grad x 1 = ¡grad x 2
= ¡D¤1 grad x 1
¤
v J2
= ¡D¤2 grad x 2
(3.135)
donde se de…nen los nuevos coe…cientes D¤i como difusividades másicas. Se deduce
enseguida que ambas difusividades, como en el caso anterior, son iguales y su relación
con D es la siguiente:
difusividad másica
M1 M2
D¤1 = D¤2 = D(x2 ) ¹
M (x2 ) V¹ (x2 )
fDi¤ g = g=s cm (3.136)
Igual que en el caso anterior, la dependencia con la concentración y/o composición
puede ser más compleja que la de D.
Finalmente es conveniente introducir en (3.135) la variable ‘natural’ de composición correspondiente a ‡ujos másicos, la fracción másica  i. Para sistemas binarios
se tiene
½
x iMi
Âi = i =
; (i = 1; 2) (Â 1 + Â2 = 1):
(3.137)
½
x 1 M1 + x 2M 2
Siendo la relación entre gradientes de Âi y de x i es la siguiente (caso binario)
µ
¶
dÂi
grad Âi =
grad x i (i = 1; 2),
(3.138)
dx i
de (3.137) se obtiene
dÂi
M1 M2
=
dx i
(xi Mi + (1 ¡ x i)M j )2
(i = 1; 2; j = 2; 1)
(3.139)
y, por lo tanto, vale
grad  i =
M1 M2
grad xi
¹ (x i)2
M
(i = 12),
(3.140)
¹ (x i) = x iMi + (1 ¡ xi )Mj ). Sustituyendo (3.140) en (3.135) con (3.136) resulta:
(M
¤
vJi
¹ (x i) M1 M2
M
= ¡D(xi ) ¹
¹ (x i) 2 grad x i )
V (xi ) M
¤
v Ji
= ¡D ½ grad  i
(i = 1; 2) (3.141)
¹ =V¹ ): La expresión (3.141) es sumamente simple y práctica, y al producto D ½
(½ = M
también se lo suele denominar ‘difusividad másica’, que no debe confundirse con la
dada por (3.136).
57
Acotación …nal. Aunque es mucho el material presentado no debe olvidarse que
vale solo para sistemas binarios y que en realidad hay un solo coe…ciente de difusión
(D) para cada concentración y/o composición y que todo lo demás son variaciones,
algunas más prácticas que otras, alrededor de esta magnitud.
Además se debe acotar que todos estos resultados valen también para componentes
electrolíticos, aunque su interpretación según la TPI es más compleja (presencia de
al menos dos constituyentes iónicos o especies iónicas cargadas eléctricamente) y se
desarrollará por separado más adelante.
3.6. Difusión en sistemas multicomponentes.
Se desarrolla en el curso de FISICOQUÍMICA ESPECIAL. (Ver sección 1)
58
3.7. Apéndice I. Relaciones entre variables de concentración:
3.7.1. Relaciones para sistemas binarios a T y P constantes.
En el campo de difusión es muy conveniente expresar y interconvertir los gradientes
de concentración entre las variables de concentración usuales. Las variables de concentración usuales son:
f racci¶
o n molar
molalidad
x2
m2
´
n2 =n
´
n2 =(n1 M 1 ) = x 2 =(x1 M 1 ) = c2 =(c1 M 1 )
molaridad
c2 ´ n2 =V = x 2 =V¹
(3.142)
P
donde n es el número total de moles (n= in i), M 1 la masa molar del solvente
({Mi }=kg/mol) y V¹ (= V =n) el volumen molar del sistema. Las relaciones entre
estas variables se deducen a continuación.
Fracción molar vs. molalidad: La relación entre estas variables es
x2 =
m 2 M1
1 + m 2M 1
x1 =
1
1 + m 2 M1
(3.143)
y por derivación se obtienen la siguiente relación entre gradientes:
grad x2 =
M1
grad m2
(1 + m 2 M1 )2
)
grad x2 =(x1 x 2 ) = grad m 2 =m2
Fracción molar vs. molaridad: A partir de la relación x i = ci V¹
sistemas binarios
grad x i
=
)
(3.144)
se obtiene para
@V¹
V¹ grad ci + ci grad V¹ = V¹ grad ci + ci
grad xi
@xi
@ V¹
(1 ¡ ci
) grad x i = V¹ grad ci
@x i
(3.145)
Para resolver esta relación se necesita la expresión termodinámica para la derivada
indicada. La misma surge de la relación entre el volumen molar y los volumenes
parciales molares, esto es,
V¹ = x 1 V 1 + x 2V 2 = V 2 + (V 1 ¡ V 2 )x1
y diferenciando, recordando que
)
=
Con (
P
i ci
=
(ec. de Gibbs-Duhem), resulta
dV¹ = V 1 dx1 + x 1 dV 1 + V2 dx 2 + x 2 dV2 =
@ V¹
(V 1 ¡ V 2 )dx 1 )
= V1 ¡ V2
@x1
=) c1 + c2 = 1= V¹
)
x 1 dV1 + x2 dV 2 = 0
y
1 = c1 V 1 + c2 V2
(3.146)
y esta relación se deduce
@ V¹
= 1 ¡ c1 (V 1 ¡ V 2 ) = 1 ¡ c1 V 1 + c1 V 2
@x 1
@ V¹
(c1 + c2 )V2 = V 2 = V¹ )
1 ¡ c1
= V 2 = V¹
@x 1
1 ¡ c1
59
(3.147)
Por lo tanto, la relación entre gradientes es
(V2 = V¹ 2 ) grad x1 = grad c1
(V 1 = V¹ 2 ) grad x2 = grad c2
(3.148)
Molaridad vs. molalidad: La relación entre molaridad y molalidad es
m 2 = c2 =(c1M 1 )
(3.149)
relación que, con las siguientes fórmulas auxiliares
½ = (n1 M1 + n2 M2 )=V = c1 M 1 + c2 M 2 = c1 M 1 (1 + m2 M 2 )
V 1 grad c1 = ¡V 2 grad c2
(3.150)
(3.151)
(½=densidad), toma las siguientes expresiones más prácticas:
)
m 2 = c2 =(½ ¡ c2 M2)
c2 = ½ m 2 =(1 + m2 M 2 )
y
(3.152)
Diferenciando la relación inicial se obtiene:
grad m2
= grad c2 =(c1 M 1 ) ¡ c2 M 1 grad c1 =(c1 M 1 )2
c2 V2
1 m2
= (1 +
) grad c2 =(c1 M 1 ) =
grad c2
c1 V1
c1 V 1 c2
(3.153)
y entonces resulta
)
grad m2 =m 2 = [grad c2 =c2 ]=(c1 V 1 )
(3.154)
3.7.2. Relaciones para sistemas multicomponentes a T y P constantes.
En el caso de más de dos componentes es conveniente tomar para el componente cuya
concentración no es independiente, en el general el solvente, el índice o. Las variables
de concentración usuales son entonces:
f racci¶on molar
xi
molalidad
mi
´
ni=n
´
ni=(no M o ) = x i =(x o M o ) = ci =(co M o )
molaridad
ci ´ ni=V = x i= V¹
(3.155)
P
donde siguen siendo n el número total de moles (n= ini ), Mo la masa molar del
solvente ({M k }=kg/mol) y V¹ (= V =n) el volumen molar del sistema. Las relaciones
entre todas las variables independientes de estos tipos se deducen a continuación.
Fracción molar - molalidad: Las relaciones entre estas variables son
mi = xi =x o M o =
y
xi =
no +
n
Pi
k6= o nk
=
1+
1
x
Pi
M o 1 ¡ k6=o xk
n =n
Mo m i
Pi o
P
) xi =
n
=n
1
+
M
k
o
o
k6=o
k6=o m k
60
(3.156)
(3.157)
con
P
k
xk = 1 y m o = 1=Mo (la molalidad del solvente es constante).
Fracción molar - molaridad: Aqui las relaciones son:
ci = xi =V¹ = P
xi
x
xi
Pi
P
P
=
=
x o V o + k6=o xk V k
(1 ¡ k6=o x k )Vo + k6= o xk V k
k x kVk
o sea
ci =
Vo +
y la inversa es
ci
x i = ci V¹ = P
k ck
=
o sea
co +
P
c
Pi
=
k6= o c k
xi =
1¡
xi
k6= o xk (V k ¡ V o )
P
1
Vo [1
¡
P
(3.158)
ci
P
c
k6=o k Vk ] +
k6=o c k
Vo ci
k6=o c k (V k ¡ V o )
(3.159)
P
P
donde se ha usado la de…nición V¹ = V =n = V = k xk = 1= k ck :
Por lo visto, en estos casos se necesita la información de todos los volúmenes
parciales molares Vk ; información que se obtiene analizando ½ = ½(ck ) = ½(xk)
(½=densidad) mediante el método general de determinación de propiedades parciales
molares (ver textos de Termodinámica Química).
Molaridad vs. molalidad: De la expresión de…nitoria general, m i = ci=(coM o ); se
deduce, recordando que
X
X
X
½=
ck Mk = co Mo +
ck M k ) coM o = ½ ¡
ck M k ;
(3.160)
k
k6=o
k6=o
queda
mi =
½¡
Y de ci = m i co Mo ; con
co Mo
=
)
½¡
X
k6=o
P
ci
k6=o c k M k
(3.161)
X
ck Mk = ½ ¡ (
m k Mk ) co M o
co M o = ½=(1 +
X
k6=o
m k M k );
(3.162)
k6=o
resulta
ci =
1+
m ½
P i
k6=o m k M k
61
(3.163)
3.8. Apéndice II. Factores termodinámicos
3.8.1. Repaso de de…niciones.
Para lograr expresiones directas de los factores termodinámicos de la difusión en las
distintas escalas del potencial químico (que utilizan, además, distintas variables de
concentración) y las relaciones entre ellos deben recordarse las expresiones usuales del
potencial químico. Estas son:
para solvente:
fracción molar
¹i = ¹²i + RT ln f ix i
(escala de Raoult)
0
= ¹1
i + RT ln f i xi
(escala de Henry)
(3.164)
para soluto:
fracción molar ¹i
molalidad
¹i
=
molaridad
¹i
=
¹ª
i + RT
¹¦i + RT
ln °i m i=my
ln yi ci=cy
(m y = 1 mol/kg solvente)
(cy = 1 mol/dm3 )
(3.165)
donde las constantes son los potenciales quíimicos del estado tipo en la escala respectiva,
estado tipo de solvente ¹²i (x i = 1)
(3.166)
y estados tipo de soluto
ª
y
¦
y
¹1
i (xi = 1); ¹i (mi = m ); ¹i (ci = c )
(3.167)
y los coe…cientes de actividad según la escala son: fi ;
, respectivamente.
Para estos últimos valen los siguientes límites (estados o rangos de referencia)
mezcla ideal:
lim fi = 1
lim ln fi = 0
(3.168)
fi0 ; ° i; y i
xi !1
solución ideal diluída:
xi!1
lim f i0
=
1
lim ° i
=
1
lim y i
=
1
xi!0
m i!0
c i!0
lim ln f i0 = 0
xi !0
lim ln °i = 0
m i!1
lim ln y i = 0
c i!0
(3.169)
3.8.2. Factores termodinámicos.
Se denominan factores termodinámicos de la difusión (FTD) al producto de las
derivadas del potencial químico de un componente respecto de una variable dada
de concentración multiplicadas por esas variables. Para explicir la derivada se toma
la expresión del potencial químico en la escala de la variable de concentración y/o
composición respecto de la cual se va a derivar. Asi se tiene
·
¸
·
¸
·
¸
@¹2
@ ln(c2 y 2 )
RT
@ ln y2 )
( c)
¹22 ´
= RT
=
[1 +
]
@c2 T ;P
@c2
c2
@ ln c2 T ;P
T ;P
(c)
)
(m)
¹22
´
)
(c)
(3.170)
c2 ¢ ¹22 = RT ¡ 2
·
@¹2
@m 2
¸
= RT
T ;P
(m)
m 2 ¹22
= RT
·
@ ln(m2 ° 2 )
@m 2
(m)
¡2
¸
=
T ;P
·
¸
RT
@ ln ° 2 )
[1 +
]
m2
@ ln m2 T ;P
(3.171)
62
(x)
¹22
´
·
)
@¹2
@x 2
¸
T ;P
·
@ ln(x 2 f2 )
= RT
@x 2
(x)
¸
T ;P
·
¸
RT
@ ln f 2 )
=
[1 +
]
x2
@ ln x2 T ;P
( x)
(3.172)
x 2 ¹22 = RT ¡2
donde
¸
@ ln f2 )
@ ln x2 T ;P
T ;P
T;P
(3.173)
Para la escala de fracción molar puede tomarse también la escala de Henry para el
potencial químico; las expresiones resultantes son equivalente ya que los coe…cientes
de actividad de Raoult y de Henry son proporcionales entre si.
Para interconvertir los FTD se recurre a la operación matemática simple de cambio
de función en una derivada y para las relaciones entre las variables se utilizan las
ecuaciones derivadas en el Apéndice I. Asi se obtiene
·
¸
·
¸
·
¸
·
¸
@¹2
@¹2
@m 2
1 m 2 @¹2
1 m 2 (m)
( c)
¹22 ´
=
=
=
¹
@c2 T ;P
@m 2 T ; P @c2 T ; P
c1 V 1 c2 @m 2 T ; P
c1 V1 c2 22
(c)
¡2 ´ 1 +
·
@ ln y2 )
@ ln c2
¸
(m)
;
¡2
´1+
(c)
) c2 ¢ ¹22 =
·
@ ln ° 2)
@ ln m 2
¸
;
(x)
¡2
´ 1+
1
(m)
[m2 ¢ ¹22 ]
c1 V1
·
(3.174)
y
(m)
¹22 ´
·
@¹2
@m 2
¸
=
T ;P
·
@¹2
@x2
¸
T;P
·
@x 2
@m 2
(m)
¸
=
T;P
·
¸
x1 x 2 @¹2
x 1 x2 (x)
=
¹
m 2 @x 2 T ;P
m2 22
(x)
) m 2 ¢ ¹22 = x1 [x 2 ¢ ¹22 ]
y combinado estas dos fórmulas entre FTD se logra la restante:
x1
V¹
[x 2 ¢ ¹(22x)] =
[x 2 ¢ ¹ (x)
22 ]
c1 V 1
V1
___________________
) c2 ¢ ¹(c)
22 =
63
(3.175)