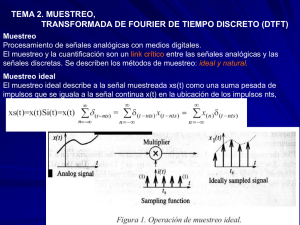
Muestreo

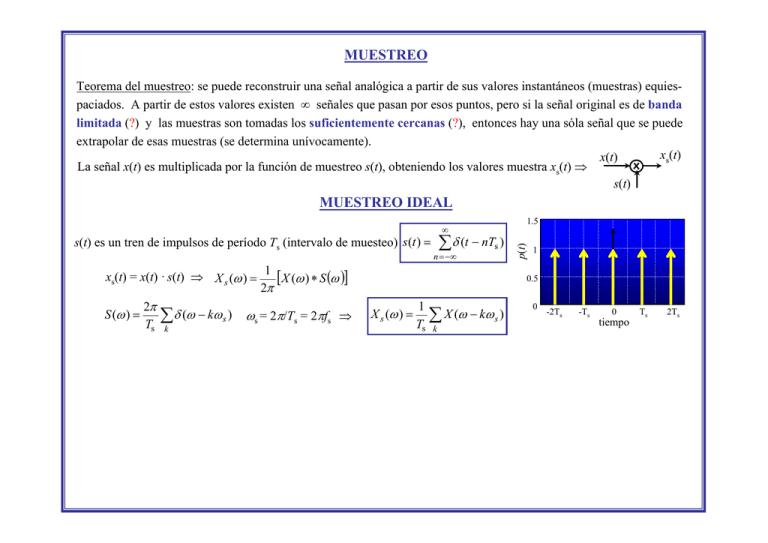
MUESTREO
Teorema del muestreo: se puede reconstruir una señal analógica a partir de sus valores instantáneos (muestras) equiespaciados. A partir de estos valores existen ∞ señales que pasan por esos puntos, pero si la señal original es de banda
limitada (?) y las muestras son tomadas los suficientemente cercanas (?), entonces hay una sóla señal que se puede
extrapolar de esas muestras (se determina unívocamente).
xs(t)
x(t)
La señal x(t) es multiplicada por la función de muestreo s(t), obteniendo los valores muestra xs(t) ⇒
s(t)
MUESTREO IDEAL
xs(t) = x(t) · s(t) ⇒ X s (ω ) =
S (ω ) =
2π
Ts
∑ δ (ω − kω s )
k
∑ δ (t − nTs )
n = −∞
1
[X (ω ) ∗ S (ω )]
2π
ωs = 2π/Ts = 2πfs ⇒
1.5
p(t)
s(t) es un tren de impulsos de período Ts (intervalo de muesteo) s (t ) =
∞
1
0.5
X s (ω ) =
1
∑ X (ω − kω s )
Ts k
0
-2Ts
-Ts
0
tiempo
Ts
2Ts
X(ω)
S(ω)
Xs(ω)
Xs(ω)
MUESTREO
Teorema del muestreo: se puede reconstruir una señal analógica a partir de sus valores instantáneos (muestras) equiespaciados. A partir de estos valores existen ∞ señales que pasan por esos puntos, pero si la señal original es de banda
limitada (?) y las muestras son tomadas los suficientemente cercanas (?), entonces hay una sóla señal que se puede
extrapolar de esas muestras (se determina unívocamente).
xs(t)
x(t)
La señal x(t) es multiplicada por la función de muestreo s(t), obteniendo los valores muestra xs(t) ⇒
s(t)
MUESTREO IDEAL
xs(t) = x(t) · s(t) ⇒ X s (ω ) =
S (ω ) =
2π
Ts
∑ δ (ω − kω s )
k
∑ δ (t − nTs )
n = −∞
p(t)
s(t) es un tren de impulsos de período Ts (intervalo de muesteo) s (t ) =
1.5
∞
1
[X (ω ) ∗ S (ω )]
2π
ωs = 2π/Ts = 2πfs ⇒
1
0.5
X s (ω ) =
1
∑ X (ω − kω s )
Ts k
0
-2Ts
-Ts
0
tiempo
Ts
2Ts
si ωs < 2ωm existe solapamiento (ALIASING). Si ωs ≥ 2ωm se puede recuperar X(ω) con un LPF ideal de ganancia Ts
fs = frecuencia de Nyquist
X(ω)
S(ω)
Xs(ω)
Xs(ω)
MUESTREO
Teorema del muestreo: se puede reconstruir una señal analógica a partir de sus valores instantáneos (muestras) equiespaciados. A partir de estos valores existen ∞ señales que pasan por esos puntos, pero si la señal original es de banda
limitada (?) y las muestras son tomadas los suficientemente cercanas (?), entonces hay una sóla señal que se puede
extrapolar de esas muestras (se determina unívocamente).
xs(t)
x(t)
La señal x(t) es multiplicada por la función de muestreo s(t), obteniendo los valores muestra xs(t) ⇒
s(t)
MUESTREO IDEAL
xs(t) = x(t) · s(t) ⇒ X s (ω ) =
S (ω ) =
2π
Ts
∑ δ (ω − kω s )
k
∑ δ (t − nTs )
n = −∞
p(t)
s(t) es un tren de impulsos de período Ts (intervalo de muesteo) s (t ) =
1.5
∞
1
[X (ω ) ∗ S (ω )]
2π
ωs = 2π/Ts = 2πfs ⇒
1
0.5
X s (ω ) =
1
∑ X (ω − kω s )
Ts k
0
-2Ts
-Ts
0
tiempo
Ts
2Ts
si ωs < 2ωm existe solapamiento (ALIASING). Si ωs ≥ 2ωm se puede recuperar X(ω) con un LPF ideal de ganancia Ts
fs = frecuencia de Nyquist
Teorema de Nyquist: si una señal de banda limitada es muestreada a una frecuencia de
por lo menos el doble de su máxima componente, ENTONCES es posible recuperarla
unívocamente (a partir de sus puntos muestra) con un filtro pasabajos ideal.
MUESTREO PRACTICO
¾La onda muestreadora está formada por pulsos que tienen amplitud y duración finitas.
¾Los filtros de reconstrucción prácticos difieren de los ideales (banda o zona de transición).
¾Los mensajes son limitados en tiempo ⇒ no pueden ser limitados en banda.
9 Pulsos: en general se emplea la técnica de muestreo y retención (Sample and Hold ≡ S&H) ⇒ Retenedor Orden Cero
x[t]
ROC
xp[t]
x(t)
s(t)
⎡
⎤
x p (t ) = ∑ x(nTs ) ⋅ p (t − nTs ) = p (t ) ∗ ⎢∑ x(nTs ) ⋅ δ (t − nTs )⎥
n
⎣n
⎦
xs(t)
p(t)
1
xp(t)
Ts
t
⎡
⎤
X p ( f ) = P( f ) ⎢ f s ∑ X ( f − kf s )⎥ = P ( f ) ⋅ X s ( f )
⎣ k
⎦
⇒ P(f) ‘pesa’al espectro de la señal muestreada y lo distorsiona en las frecuencias superiores ≡ efecto de apertura. Si el
efecto es muy grande se puede corregir por medio de un filtro ecualizador Heq(f) = 1/P(f) (si 1/τ >> W no es necesario).
Para el ROC:
p(t)
1
Ts
0 ≤ t ≤ Ts
∀t
⎧1
p (t ) = ⎨
⎩0
t
⎡ 2 sin (ω Ts / 2 )⎤
P (ω ) = e − jω Ts / 2 ⎢
⎥⎦
ω
⎣
X(ω)
Xp(ω)
Xs(ω)
P(ω)
Heq(ω)
⇒ H eq (ω ) = 1
P(ω )
1
-ωs /2
ωs /2
ω
MUESTREO PRACTICO
¾La onda muestreadora está formada por pulsos que tienen amplitud y duración finitas.
¾Los filtros de reconstrucción prácticos difieren de los ideales (banda o zona de transición).
¾Los mensajes son limitados en tiempo ⇒ no pueden ser limitados en banda.
9 Pulsos: en general se emplea la técnica de muestreo y retención (Sample and Hold ≡ S&H) ⇒ Retenedor Orden Cero
x[t]
ROC
xp[t]
x(t)
s(t)
⎡
⎤
x p (t ) = ∑ x(nTs ) ⋅ p (t − nTs ) = p (t ) ∗ ⎢∑ x(nTs ) ⋅ δ (t − nTs )⎥
n
⎣n
⎦
xs(t)
p(t)
1
xp(t)
Ts
t
⎡
⎤
X p ( f ) = P( f ) ⎢ f s ∑ X ( f − kf s )⎥ = P ( f ) ⋅ X s ( f )
⎣ k
⎦
⇒ P(f) ‘pesa’al espectro de la señal muestreada y lo distorsiona en las frecuencias superiores ≡ efecto de apertura. Si el
efecto es muy grande se puede corregir por medio de un filtro ecualizador Heq(f) = 1/P(f) (si 1/τ >> W no es necesario).
9 Filtros de reconstrucción reales: se recurre al empleo de bandas de seguridad ⇒ incrementar ωs
9 Señal NO limitada en banda: se debe asegurar que la señal no tenga componentes superiores a ωs/2 ⇒ se aplica un
filtro pasabajos en la entrada ≡ Filtro anti-aliasing (es el peor inconveniente porque modifica la información).
Submuestreo
Sea la señal x(t) = cos(ω0t)
muestreada a ωS constante
(ωS < 2ω0). Se analiza que
sucede a medida que ω0↑
Para ω0 > ωS/2 se produce el
traslape y la frecuencia original
original asume la identidad de
una frecuencia inferior (ωS - ω0).
Para ωS/2 < ω0 < ωS , a medida
que ω0↑ la frecuencia de salida
(ωS-ω0)↓ ≡ efecto estroboscópico
(uso: osciloscopio de muestreo,
voltímetro vectorial).
INTERPOLACION
Interpolación ≡ reconstrucción (aproximada ó exacta) de una función a partir de sus muestras.
Interpolación Orden Cero
1
1
0.5
0.5
Amplitud
Amplitud
¾ Retenedor de Orden Cero:
retiene el valor de la muestra
hasta la próxima. Es el más
simple.
Señal muestreada
0
0
-0.5
-0.5
-1
-1
¾ Interpolación Lineal: los
puntos adyacentes se conectan
con una línea recta.
600
700
800
900
1000 1100 1200 1300 1400
600
tiempo
1
1
0.5
0.5
0
-0.5
800
900
1000 1100 1200 1300 1400
tiempo
Interpolación Sinc
Amplitud
¾ Interpolación de mayor Orden:
los puntos se unen mediante
polinomios de grado mayor u
otras funciones matemáticas.
Amplitud
Interpolación Primer Orden
700
0
-0.5
-1
-1
¾ Interpolación Sinc: cada muestra
600 700 800 900 1000 1100 1200 1300 1400
600 700 800 900 1000 1100
corresponde al peso de una sinc
tiempo
tiempo
centrada en el instante de muestreo,
y los valores intermedios se otienen sumando las contribuciones de cada una de estas funciones.
1200 1300 1400
INTERPOLACION SINC
Para reconstruir espectralmente la señal se emplea un LPF ideal
Xr(ω)
⇒ Xr(f) = Xs(f)·H(f) con H(f) = rect [f /( 2fc)] y fc = fs/2
xr (t ) = xs (t ) ∗ h(t )
= h(t ) ∗ ∑ x(nTs ) ⋅ δ (t − nTs )
n
= ∑ x(nTs ) ⋅ h(t − nTs )
n
1
Tω
⎛ω t ⎞
hr (t ) = s c sinc⎜ c ⎟
π
⎝ π ⎠
0.5
Tω
⎡ω (t − nTs ) ⎤
xr (t ) = ∑ x(nTs ) s c sinc ⎢ c
⎥⎦
π
π
⎣
n
considerando fc = fs/2:
xr (t ) = ∑ x(nTs ) ⋅ sinc( f st − n )
n
0
-0.5
tiempo
Xs(ω)
H(ω)
CALCULO DE LA INTERPOLACION SINC
Para la implementación de la expresión xr (t ) = ∑ x(nTs ) ⋅ sinc( f st − n ) deben fijarse parámetros para sustiruir la variable
contínua t por su equivalente discreta:
n
¾ Cantidad de muestras por ciclo de la máxima componente de la señal ⇒ n_muestras
¾ Cantidad de valores a intercalar entre dos valores muestra consecutivos ⇒ n_puntos
¾ Cantidad de muestras a considerar como “historia” (valores pasados y futuros) de la señal ⇒ n_historia
Cada intervalo de muestreo debe dividirse en (n_puntos + 1) intervalos:
Reemplazando t por k·Δt (1 ≤ k ≤ n_puntos):
xr (k ⋅ Δt ) =
Debe agregarse otro índice para el desplazamiento
dentro del registro de valores adquiridos (j) ⇒
x • •
Ts
• Δt• x
Ts = (n_puntos+1)·Δt
⎡
⎤
k
− n⎥
x(nTs ) ⋅ sinc ⎢
n = − n_historia +1
⎣ n_puntos + 1 ⎦
n_historia
∑
xr ( jTs + k ⋅ Δt ) =
⎡
⎤
k
− n⎥
x(( j + n)Ts ) ⋅ sinc ⎢
n = − n_historia +1
⎣ n_puntos + 1 ⎦
n_historia
∑
%programa para reconstruir señales muestreadas
%reconstructor de orden cero
clear
n0=99;
f=10; %frecuencia
hist=4; %cantidad de sinc para reconstrución
d=0.2; % distancia entre puntos interpolados (0 y 1- 0.2 indica 5 puntos)
n=0:n0;
Y=[];
y=sin(2*pi*f*n/(n0+1));
subplot(2,2,1)
plot(y,'.')
title 'Puntos Muestra'
for k=1:n0+1,
for i=1:(1/d)-1;
y1(i)=y(k);
end
Y=[Y y1];
end
subplot(2,2,2)
plot(Y)
title 'Reconstructor de Orden 0'
%reconstructor sinc
Y5=[];
for k=1+hist:n0-hist,
for u=0:d:1-d;
sum=0;
for s=-hist:hist,
sum=sum+y(k+s)*sinc(u-s);
end
Y5=[Y5 sum];
end
end
subplot(2,2,4)
plot(Y5)
title 'Reconstructor sinc'
%reconstructor lineal
Y2=[];
for k=1:n0,
i1=1;
for i=1+d:d:2,
y2(i1)=(y(k+1)-y(k))*i-y(k+1)+2*y(k);
i1=i1+1;
end
Y2=[Y2 y2];
end
subplot(2,2,3)
plot(Y2)
title 'Reconstructor lineal'
CAMBIO DE LA FRECUENCIA DE MUESTREO
La señal de tiempo contínuo xc(t) puede representarse por una secuencia x[n] = xc[nTs]. Se quiere cambiar fs obteniendo
una nueva secuencia x’[n] = xc[nTs’]. El método indirecto sería:
x[n]
fs
xc(t)
DAC +
Filtro Interp.
x’[n]
ADC
fs’
(complejo!!)
¾ DIEZMADO por un factor entero: se disminuye la frecuencia de muestreo (“muestreándola” cada M valores).
xd[n] = x[nM] = xc[nMTs] ≡ compresor de frecuencia de muestreo
x[n]
⇒ xd[n] es la que se obtendría muestreando xc(t) con período Ts’= M·Ts
Ts
Recordando el espectro X(ω) de la secuencia x[n] (valores muestra): X (ω ) =
análogamente puede escribirse el espectro Xd(ω) para xd[n] : X d (ω ) =
↓M
xd[n]
Ts’= M·Ts
1
1
2π k
X (ω − kω s ) = ∑ X (ω −
)
∑
Ts k
Ts k
Ts
1
∑ X (ω −
T'
s r
2π r
Ts'
)=
1
MTs
∑ X (ω −
r
rω s
)
M
para que no exista solapamiento (ωs/M) ≥ ωmax ⇒ la frecuencia de Nyquist original debe ser M veces mayor !!
Ejemplo: si ωs = 4 ωmax , el máximo diezmado para no tener solapamiento es M = 2
Diezmado con M = 2.
Se verifica que no existe
solapamiento.
Si se quiere utilizar un M superior habrá que garantizar
x[n]
que la señal no tenga un contenido espectral mayor que
Ts
ωs/M mediante el empleo de un filtro pasabajos digital .
LPF
G =1
ωc=π/M
~
x [ n]
Ts
↓M
~
x d [ n] = ~
x [nM ]
Ts’= M·T
Sistema para reducir la frecuencia de muestreo en M
Diezmado con M = 3.
Aparece solapamiento.
Diezmado con M = 3 y
filtrado previo para evitar
el solapamiento.
¾ INTERPOLACION por un factor entero: se aumenta la frecuencia de muestreo (insertando L valores entre muestras).
⎧⎪ x[n / L]
xe [n] = ⎨
⎪⎩0
n = 0, ± L ,±2 L
≡
xe [n] = ∑ x[k ] ⋅ δ [n − kL]
k
en el resto
los valores intermedios se generan mediante una función de reconstrucción ≡ LPF de ganancia L y ωc = π/L
x[n]
Ts
xe[n]
↑L
Ts’= Ts/L
xi[n]
LPF
G =L
ωc=π/L
Ts’= Ts/L
xi[n] = x[n/L] = xc[nTs/L] ≡ expansor de frecuencia demuestreo
Sistema para incrementar la frecuencia de muestreo en L
El análisis en el dominio de la frecuencia se realiza mediante el cálculo de la Transformada de Fourier (TF), definida por:
X (ω ) = ∑ x[n] ⋅ e − jω n
n
⇒
⎛
⎞
X e (ω ) = ∑ ⎜ ∑ x[k ]δ [n − kL] ⎟e− jω n = ∑ x[k ] ⋅ e− jω Lu = X (ωL)
⎜
⎟
u ⎝ k
u
⎠
⇒ La Transformada de Fourier de la salida del expansor es una versión escalada en frecuencia de la T.F. de la entrada.
La fórmula de interpolación para xi[n] en función de x[n] es: hi [n] =
sen(πn / L)
πn / L
⎧⎪1 − n / L
En algunos casos se pueden utilizar funciones más simples, como la lineal: hi [n] = ⎨
⎪⎩0
n≤L
resto
Interpolación en el dominio de la frecuencia
CAMBIO DE LA FRECUENCIA DE MUESTREO POR UN FACTOR NO ENTERO
Es una combinación de las técnicas de diezmado e interpolación.
x[n]
xc[n]
↑L
Ts
Ts/L
LPF
G =L
ωc=π/L
xi[n]
Ts/L
LPF
G =1
ωc=π/M
Interpolador
x[n]
Ts
↑L
~
xi [n]
↓M
TsM/L
Ts/L
Diezmador
LPF
G =L
ωc=min(π/L, π/M)
Funciones utilizadas en Matlab®:
¾ DECIMATE: Resample data at a lower rate after lowpass filtering.
¾ INTERP: Resample data at a higher rate using lowpass interpolation
¾ RESAMPLE: Change the sampling rate of a signal.
↓M
~
xd [n]
~
xd [n]
TsM/L
LABORATORIO 1Muestreo
//Programa que efectua la conversión ADC - DAC
// Declaración de las variables
unsigned int VIK=0;
// Ajuste de los conversores ADC y DAC
void setup()
{
analogReadResolution(12);
analogWriteResolution(12);
}
// Lazo de ejecución continua
void loop()
{
VIK = analogRead(A0);
analogWrite(DAC0, VIK);
}