Invarianza galileana

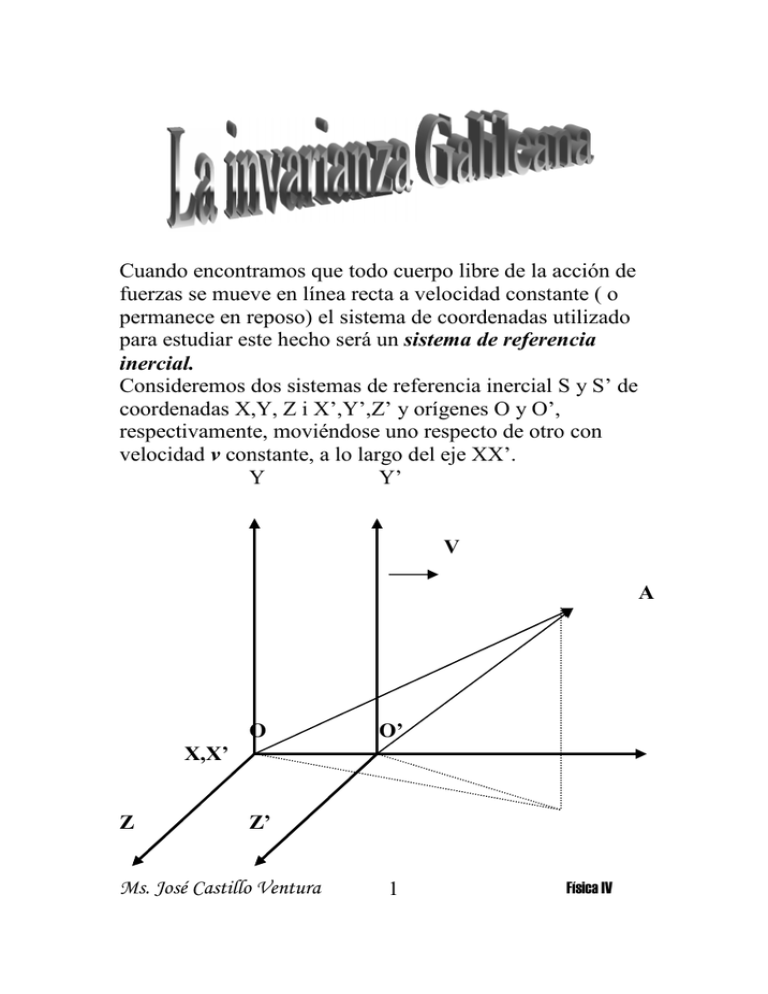
Cuando encontramos que todo cuerpo libre de la acción de
fuerzas se mueve en línea recta a velocidad constante ( o
permanece en reposo) el sistema de coordenadas utilizado
para estudiar este hecho será un sistema de referencia
inercial.
Consideremos dos sistemas de referencia inercial S y S’ de
coordenadas X,Y, Z i X’,Y’,Z’ y orígenes O y O’,
respectivamente, moviéndose uno respecto de otro con
velocidad v constante, a lo largo del eje XX’.
Y
Y’
V
A
O
O’
X,X’
Z
Z’
Ms. José Castillo Ventura
1
Física IV
En t = 0. O = O’

 

r = xi + yj + zk




r ' = x' i + y ' j + z ' k


v = vi
1.1
De la figura :
  
r = r '+v t ...1.2 Relación directa.
  
r ' = r - v t ... 1.3 Relación inversa
De 1.1 y 1.3 :




 

x' i + y ' j + z ' k = xi + yj + zk − vti ....4
x' = x − vt
y' = y
z' = z
t'= t
..1.5 Transformaciones
galileanas
Derivando las ecuaciones anteriores respecto a t’ = t
dx' dx
=
− v → v' x ' = vx − v
dt
dt
dy´' dy
=
→ v' y ' = vy ....
dt
dt
dz ' dy
=
→ v' z ' = vz
dt
dt
Ms. José Castillo Ventura
..1.6 Transformaciones de velocidad
2
Física IV
Al dividir 1.6 respecto al tiempo:
dvx ' dx'
=
− vt → ax ' = ax
dt
dt
dvy ' dvy
=
→ ay ' = ay
dt
dt
dvz ' dvz
=
→ az ' = az
dt
dt
...1.7 La aceleración permanece
INVARIANTE
Del resultado anterior podemos deducir que la aceleración
permanece invariante ante las transformaciones de Galileo, lo
cual implica que las leyes de la Física se cumplen en ambos
sistemas.
En el caso que la partícula A se mueva a lo largo del eje OX,
tendremos:
v' x ' = vx − v
v' y ' = vy = 0
...1.8
v' z ' = vz = 0
Considerando que la partícula se mueva paralelamente al eje
OY :
Teniendo en cuenta que en t=t’=0, ambos orígenes coinciden
(O = O’), entonces al alejarse S’ con velocidad v :
Ms. José Castillo Ventura
3
Física IV
Y
Y’
•
O’
X,X’
vy = v v ≡ Velocidad de A observada desde O
vy = 0 v' ≡ Velocidad de A observada desde O'
vz = 0
v' y ' = v
...1.9
vz ' = −v (Recordando que v' x ' = vx − v → v' x ' = −v
De la figura 1.2 :
(
)
v' = vx 2 + v 2
Ejemp 1: Dos trenes A y B se desplazan en rieles paralelos a
70 km/h y a 90 km/h, respectivamente. Calcular la velocidad
relativa de B respecto de A, cuando (a) se mueven en la
misma dirección; (b) cuando se mueven en direcciones
contrarias.
Solución:
Ms. José Castillo Ventura
4
Física IV
Como existe movimiento en un solo eje consideramos el
siguiente esquema:
Y
Y’
v
B
A
VA
XX’
V’B
VB
VA + V’B = VB
⇒
V’B = VB - VA
(a) Cuando se mueven en la misma dirección:
Sabemos que : V’ = V – v ⇒ V’B = VB - v = (90-70)km/h
V’B = 20 km/h.
(b) Cuando se mueven en direcciones opuestas :
Ms. José Castillo Ventura
5
Física IV
Y
Y’
XX’
v
B
A
VA
-V’B
-VB
VA – V’B = - VB Sabemos que: V’ = V – v ⇒ -V’ = - V + v
Luego: V’B = VB + v = (90 + 70) km/h
V’B = 160 km/h.
2.- Una partícula en un sistema esacionarioS1 tiene una
posición dada por x1 = 30t1 + 10t12 , donde t1 se expresa en
segundos y x1 en metros. Encuentre las expresiones para la
posición, velocidad y aceleración medidas por un
observador que se mueve en dirección x positiva a la
velocidad de 100 m/s. Suponga que t1 = t2 = 0 cuando los
sistemas S1 y S2 coinciden.
S1
x1 m
t1seg
Ms. José Castillo Ventura
6
Física IV
y1
y2
x2 = ?
v2 = ?
a2 = ?
v = 100 m/s
t1 = t2 (S1 = S2)
x1 = 30t1 + 10t12
vt
x2
x1, x2
x1
x1 = x2 + vt
x2 = x1 - vt ⇒ x2 = 30t + 10 t2 -100t
x2 = (10 t2 - 70 t) m
dx 2
= v 2 = (20t − 70)m / s
dt
dv 2
= a 2 = 20m / s 2
dt
Ms. José Castillo Ventura
7
Física IV