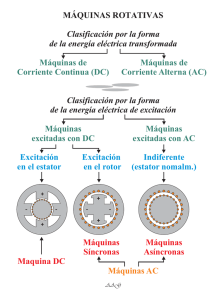
Estudio del control de velocidad y torque de un motor de inducción

PONTIFICIA UNIVERSIDAD CATÓLICA DE VALPARAÍSO - CHILE
ESCUELA INGENIERÍA ELÉCTRICA
ESTUDIO DEL CONTROL DE VELOCIDAD Y TORQUE DE UN MOTOR DE
INDUCCIÓN TRIFÁSICO APLICANDO LA TÉCNICA DE CONTROL
VECTORIAL INDIRECTO EN TENSIÓN CON Y SIN SENSOR DE
POSICIONAMIENTO
ANTONIO ALEJANDRO CASTILLO PIÑONES
INFORME FINAL DE PROYECTO
PRESENTADO EN CUMPLIMIENTO
DE LOS REQUISITOS PARA OPTAR
AL TÍTULO PROFESIONAL DE
INGENIERO CIVIL ELECTRÓNICO.
DICIEMBRE 2011
2
ESTUDIO DEL CONTROL DE VELOCIDAD Y TORQUE DE UN MOTOR DE
INDUCCIÓN TRIFÁSICO APLICANDO LA TÉCNICA DE CONTROL
VECTORIAL INDIRECTO EN TENSIÓN CON Y SIN SENSOR DE
POSICIONAMIENTO
INFORME FINAL
Presentado en cumplimiento de los requisitos
para optar al título profesional de
Ingeniero Civil Electrónico
otorgado por la
Escuela de Ingeniería Eléctrica
de la
Pontificia Universidad Católica de Valparaíso
Antonio Alejandro Castillo Piñones
Profesor Guía:
Sr. Domingo Ruiz Caballero.
Profesor Correferente 1: Sr. René Sanhueza Robles.
Profesor Correferente 2: Sr. Miguel López González.
DICIEMBRE 2011
3
ACTA DE APROBACIÓN
La Comisión Calificadora designada por la Escuela de Ingeniería Eléctrica ha
aprobado el texto del Informe Final del Proyecto de Titulación, desarrollado entre
el segundo semestre del 2009 y el segundo semestre del 2010, y denominado.
ESTUDIO DEL CONTROL DE VELOCIDAD Y TORQUE DE UN MOTOR DE
INDUCCIÓN TRIFÁSICO APLICANDO LA TÉCNICA DE CONTROL
VECTORIAL INDIRECTO EN TENSIÓN CON Y SIN SENSOR DE
POSICIONAMIENTO
Presentado por el Señor
Antonio Alejandro Castillo Piñones
Domingo Ruiz Caballero
Profesor Guía
Rene Sanhueza Robles
Segundo Revisor
Héctor Peña Mcleod
Secretario Académico
Valparaíso, Diciembre 2011
4
ESTUDIO DEL CONTROL DE VELOCIDAD Y TORQUE DE UN MOTOR DE
INDUCCIÓN TRIFÁSICO APLICANDO LA TÉCNICA DE CONTROL
VECTORIAL INDIRECTO EN TENSIÓN CON Y SIN SENSOR DE
POSICIONAMIENTO
Antonio Alejandro Castillo Piñones
Profesor Guía Sr. Domingo Ruiz Caballero
RESUMEN
Hasta hace algunos años el principal motor utilizado en procesos de
velocidad variable era el motor de corriente continua por su facilidad en la forma
de controlar la posición y la velocidad. Por otra parte el motor de inducción es el
más utilizado en procesos de velocidad constante, por su construcción simple y
robusta. Sin embargo, el modelo eléctrico que caracteriza su comportamiento
dinámico es fuertemente no lineal, multivariable y altamente acoplado lo que
naturalmente torna complejo el control de velocidad.
Con la llegada de la electrónica de potencia se abre una ventana para
entregar una solución a esta desventaja. Además integrando la aplicación de la
técnica de control vectorial se ha logrado extrapolar la técnica de control de los
motores de corriente continua al ámbito de los motores de inducción.
En el siguiente estudio, mediante el programa de simulación MATLABSIMULINK, se realizarán simulaciones del control vectorial aplicado a un motor
de inducción trifásico de baja tensión mediante un inversor multinivel hibrido
simétrico alimentado en tensión, realizando un estudio en donde se desarrollarán
aplicaciones de modulación PWM sinusoidal, PWM vectorial, muestreando la
velocidad del rotor y estimando, en base a los valores de tensión y corriente en
el estator, la velocidad del rotor.
5
ÍNDICE
INTRODUCCIÓN
Pagina
1
CAPÍTULO 1
LAS TRANSFORMADAS DE CLARK Y PARK
1.1 TRANSFORMACIÓN DE CLARK
1.2 TRANSFORMACIÓN DE PARK
2
2
2
6
CAPÍTULO 2
MODELO MATEMÁTICO MOTOR INDUCCIÓN JAULA DE
ARDILLA
2.1 MODELO DE LA MÁQUINA EN MARCO DE REFERENCIA
ARBITRARIO
2.2 PARÁMETROS DEL MOTOR DE INDUCCIÓN
2.3 ANÁLISIS MATEMÁTICO
2.4 SIMULACIONES EN MATLAB SIMULINK.
9
9
16
17
19
CAPÍTULO 3
EL CONTROL VECTORIAL
3.1 INTRODUCCIÓN AL CONTROL VECTORIAL
3.2 CONTROL DE CAMPO ORIENTADO
3.3 MODELO DE CONTROL A UTILIZAR
3.4 DEFINICIÓN DE LAS PLANTAS PARA LAZOS DE CONTROL
3.4.1 Plantas de corriente
3.4.2 Planta de velocidad
3.4.3 Planta de flujo
3.5 DISEÑO DE LOS CONTROLADORES APLICADOS
3.5.1 Controlador PI de corriente
3.5.2 Controlador PI de flujo
3.5.3 Controlador PI de velocidad
3.5.4 Controlador PI mas antiarrollamiento (Antiwindup)
3.6 SIMULACIÓN CONTROL VECTORIAL EN MATLAB-SIMULINK
3.6.1 Simulación a torque constante
3.6.2 Simulación del sistema a velocidad y torque variable
3.7 CONTROL VECTORIAL SIN SENSOR DE POSICIONAMIENTO
31
31
31
31
35
35
36
37
38
38
38
39
39
40
41
41
42
43
CAPÍTULO 4
EL ALGORITMO DE MODULACIÓN VECTORIAL
4.1 MODULACIÓN VECTORIAL
4.2 ALGORITMO DE MODULACIÓN VECTORIAL APLICADA A UN
INVERSOR DE DOS NIVELES
4.3 ALGORITMO IMPLEMENTADO EN MATLAB – SIMULINK
56
56
56
56
9
59
6
4.4 ALGORITMO DE MODULACIÓN VECTORIAL PARA UN
INVERSOR NPC DE TRES NIVELES DE TENSIÓN
4.5 ALGORITMO IMPLEMENTADO EN MATLAB SIMULINK PARA
UN INVERSOR NPC ALIMENTADO EN TENSIÓN
4.6 NUEVOS ALGORITMOS DE MODULACIÓN VECTORIAL
PARA INVERSORES MULTINIVEL
4.6.1 Algoritmo de modulación vectorial CSV-PWM
4.6.2 Obtención de las señales de referencia mediante
programación matemática
4.7 APLICACIÓN DE LA CSV-PWM EN UN INVERSOR
MULTINIVEL
4.7.1 Inversor multinivel hibrido simétrico
4.7.2 Implementación en simulink de la CSV-PWM
4.7.3 Aplicación del control vectorial mas modulación CSV-PWM
con un inversor multinivel hibrido simétrico
4.7.4 Comparación de las corrientes en el estator con diferentes
modulaciones e inversores
61
CONCLUSIÓN
80
BIBLIOGRAFÍA
81
APÉNDICE A
TIEMPOS DE CONMUTACIÓN
63
63
64
65
68
68
69
69
69
A-1
A-1
7
GLOSARIO DE TÉRMINOS
T : Torque electromotriz. [N-m]
K P : Constante de proporcionalidad. [-]
: Flujo magnético. [Wb]
I i : Corriente continúa en el inducido. [A]
M
I e : Corriente continúa en el campo. [A]
Ea : Tensión inducida. [V]
K v : Constante de proporcionalidad. [-]
r
: Velocidad mecánica rotor. [Rad/s]
Ns : Espiras por polo por fase.
k w : Factor de devanado. [-]
ia : Corriente sinusoidal fase a. [A]
ib : Corriente sinusoidal fase b. [A]
ic : Corriente sinusoidal fase c. [A]
I A : Amplitud de la corriente ia . [A]
I B : Amplitud de la corriente ib . [A]
I C : Amplitud de la corriente ic . [A]
Fm
Magnetomotriz : Distribución sinusoidal magnetomotriz. [N-m]
Fm : Amplitud de la fuerza magnetomotriz. [N-m]
F : Amplitud de la fuerza magnetomotriz en el eje alfa. [N-m]
F : Amplitud de la fuerza magnetomotriz en el eje beta. [N-m]
i
: Corriente en el eje alfa. [A]
i
: Corriente en el eje beta. [A]
i0
: Corriente de secuencia cero. [A]
T
0
T
0
: Transformada a ejes estacionarios.
1
: Transformada inversa de ejes estacionarios.
iq : Corriente en el eje de cuadratura. [A]
id : Corriente en el eje directo. [A]
Tdq 0 : Transformada en eje directo y cuadratura.
8
Tdq 0 1 : Transformada inversa en eje directo y cuadratura.
Ns : Número de vueltas efectivas del estator
Nr : Número de vueltas efectivas del rotor.
: Velocidad angular. [Rad/s]
: Velocidad angular sincrónica. [Rad/s]
e
qr
: Enlaces de flujo en el rotor en eje de cuadratura referido al estator. [Wb]
qr
: Enlaces de flujo en el rotor en eje de cuadratura. [Wb]
dr
: Enlaces de flujo en el rotor en eje directo referido al estator. [Wb]
dr
: Enlaces de flujo en el rotor en eje directo. [Wb]
i
qr
: Corriente en el rotor en el eje de cuadratura referido al estator. [A]
iqr
: Corriente en el rotor en eje de cuadratura. [A]
i
dr
: Corriente en el rotor en eje directo referido al estator. [A]
idr : Corriente en el rotor en eje directo [A]
L lr : Inductancia de dispersión del rotor referida al estator [H].
Llr : Inductancia de magnetización del rotor [H].
R r : Resistencia del rotor referida al estator [H].
Rr : Resistencia del Rotor [Ohm]
vqs
Rs
iqs
: Tensión en el estator en eje de cuadratura. [V]
: Resistencia en el estator.
: Corriente en el estator en eje de cuadratura. [A]
qs
ds
vds
ids
: Enlaces de flujo en el estator en eje de cuadratura. [Wb]
: Enlaces de flujo en el estator en eje directo. [Wb]
: Tensión en el estator en eje directo. [V]
: Corriente en el estator en eje directo. [A]
ds
: Flujo enlazado en el estator en eje directo. [Wb]
9
qs
: Flujo enlazado en el estator en eje de cuadratura. [Wb]
v0s
i0s
: Tensión de secuencia cero. [V]
: Corriente de secuencia cero. [A]
0s
v
: Flujo enlazado de secuencia cero. [Wb]
qr
r
: Velocidad angular eléctrica en el rotor. [Rad/s]
v
dr
v
0r
i
: Tensión en el rotor referida al estator en eje de cuadratura. [V]
: Tensión en el rotor referida al estator en eje directo. [V]
: Tensión de secuencia cero en el rotor referido al estator. [V]
0r
: Corriente de secuencia cero el rotor referido al estator. [A]
0r
: Flujo enlazado de secuencia cero referido al estator. [Wb]
Lls
: Inductancia de magnetizante del estator. [H]
Lm
: Inductancia mutua. [H]
Llr : Inductancia magnetizante del rotor. [H]
Ls : Inductancia en el estator. [H]
Lr : Inductancia en el rotor. [H]
Pin
: Potencia de entrada. [W]
vas : Tensión instantánea fase a. [V]
ias : Corriente instantánea fase b. [A]
vbs : Tensión instantánea fase b. [V]
ics : Corriente instantánea fase c. [A]
v
ar
: Tensión instantánea fase a en el rotor referida al estator. [V]
i
ar
: Corriente instantánea fase a en el rotor referida al estator. [A]
v
br
: Tensión instantánea fase b en el rotor referida al estator. [V]
i
br
: Corriente instantánea fase b en el rotor referida al estator. [A]
v
cr
: Tensión instantánea fase c en el rotor referida al estator. [V]
i
cr
: Corriente instantánea fase c en el rotor referida al estator. [A]
Tem : Torque electromagnético. [N-m]
10
P : Pares de polos.
: Enlaces de flujo por vuelta en el estator en eje de cuadratura. [Wb*Rad/s]
qs
b
: Velocidad angular base. [Rad/s]
qs
: Flujo enlazado en el estator en eje de cuadratura. [Wb]
ds
: Flujo por vuelta o espira en el estator en eje directo. [Wb*Rad/s]
ds
: Enlace de flujo en el estator en eje directo. [Wb]
0s
: Flujo por vuelta de secuencia cero. [Wb*Rad/s]
0s
: Enlaces de flujo de secuencia cero. [Wb]
: Flujo por vuelta en el rotor en eje de cuadratura referido al estator.
[Wb*Rad/s]
qr
qr
: Enlaces de flujo en el rotor en eje de cuadratura referido al estator. [Wb]
dr
: Flujo por vuelta en el rotor en eje directo referido al estator.
[Wb*Rad/s]
: Enlaces de flujo en el rotor en eje directo referido al estator. [Wb]
dr
: Flujo por vuelta de secuencia cero en el rotor referido al estator.
[Wb*Rad/s]
0r
: Enlaces de flujo de secuencia. [Wb]
0r
qm
qm
: Enlace de flujo magnetizante en eje de cuadratura. [Wb]
dm
dm
X ls
X
: Flujo magnetizante por vuelta en eje de cuadratura. [Wb*Rad/s]
: Flujo magnetizante por espira en eje directo. [Wb*Rad/s]
: Enlace de flujo magnetizante en eje directo. [Wb]
: Reactancia de dispersión del estator. [Ohm]
lr
: Reactancia de dispersión del rotor referida al estator. [Ohm]
X m : Reactancia de magnetización.
Xs
X
[Ohm]
: Reactancia del estator. [Ohm]
r
: Reactancia del rotor referida al estator. [Ohm]
qm
: Flujo por espira magnetizante en eje de cuadratura [Wb*Rad/s]
VsQ : Tensión en el estator en eje de cuadratura en marco de referencia
estacionario. [V]
VsD : Tensión en el estator en eje directo en marco de referencia estacionario. [V]
rmech : Velocidad mecánica del rotor. [Rad/s]
11
s
: Velocidad sincrónica del motor. [Rad/s]
ka : Coeficiente de proporcionalidad [-]
I a : Corriente de armadura. [A]
If
: Corriente de campo. [A]
(I f )
: Flujo de campo. [Wb]
vao : Tensión fase neutro inversor. [V]
vbo : Tensión fase neutro inversor. [V]
vco : Tensión fase neutro inversor. [V]
van : Tensión fase neutro carga. [V]
vbn : Tensión fase neutro carga. [V]
vcn : Tensión fase neutro carga. [V]
E: Tensión en el puente de continua. [V]
V1
: Vector activo de tensión 1. [V]
T1 : Tiempo de ciclo útil de vector V1 . [S]
V2
: Vector activo de tensión 2. [V]
T2 : Tiempo de ciclo útil de vector V2 . [S]
Vs
: Vector espacial de referencia. [V]
Ts : Periodo. [s]
T0 : Tiempo de ciclo útil vector nulo. [S]
S1 : Interruptor 1.
S2 : Interruptor 2.
S3 : Interruptor 3.
12
LISTADO DE FIGURAS
1-1 Devanado concentrado de paso diametral
1-2 Proyección sobre los ejes “ ”y “ ”.
1-3 Ejes d y q.
2-1 Marco de referencia arbitrario que gira a una velocidad
2-2 Circuito equivalente en ejes qd0.
2-3 Ecuación para flujo qs
2-4 Ecuación para flujo
ds
2-5 Ecuación para flujo
qr
2-6 Ecuación para flujo
dr
2-7 Ecuación para flujo
mq
2-8 Ecuación para flujo
md
isq
2-10 Ecuación para la corriente isd
2-11 Ecuación para la corriente irq
2-12 Ecuación para la corriente ird
2-13 Ecuación para el torque Te
2-9 Ecuación para la corriente
2-14 Ecuación para la velocidad r
2-15 Modelo completo motor de inducción.
2-16 Ecuación de la transformada de CLARK.
2-17 Ecuación de la transformada de PARK
2-18 Sistema completo motor de inducción
2-19 Tensión Vds , Vqs .
2-20 Tensiones sinusoidales en el estator.
2-21Corrientes sinusoidales del estator.
2-22 Velocidad sincrónica y velocidad mecánica en el rotor.
2-23 Corriente isq .
isd .
2-25 Corriente irq
2-26 Corriente ird
2-24 Corriente
2-27 Enlace de flujo
qs
2-28 Enlace de flujo
ds
2-29 Enlace de flujo
qr
,
13
2-30 Enlace de flujo dr
3-1 Maquina de corriente continua de excitación independiente.
3-2 Marco de referencia sincrónico alineado con el campo del rotor.
3-3 Método de control indirecto por fuente de tensión
3-4 Respuesta al escalón unitario planta de corriente
3-5 Respuesta al escalón unitario planta de flujo
3-6 Respuesta al escalón unitario planta de velocidad
3-7 Controlador proporcional e integral
3-8 Respuesta del controlador proporcional e integral
3-9 Controlador proporcional e integral + Anti arrollamiento
3-10 Respuesta del controlador proporcional e integral + Anti arrollamiento
3-11 Modelo general control vectorial aplicado al motor de inducción
3-12 Respuesta del motor de inducción a la referencia de velocidad
3-13 Tensión de fase neutro a inversor de dos niveles.
3-14 Tensión de línea de tres niveles
3-15 Torque electromagnético del motor
3-16 Corriente en el eje de cuadratura del estator
3-17 Flujo en el eje directo del rotor
3-18 Corriente trifásica en el estator en referencia a la velocidad del motor
3-19 Corriente trifásica en el estator
3-20 Corriente en el eje directo del estator
3-21 Velocidad angular del campo en el estator
3-22 Variación de torque en la carga y de velocidad
3-23 Torque electromecánico
3-24 Variación de la corriente en el estator en función de la carga
3-25 Corrientes trifásicas en el estator.
3-26 Corriente en el eje de cuadratura del estator
3-27 Corriente en el eje directo del estator
3-28 Velocidad angular del campo
3-29 Flujo en el eje directo del rotor
3-30 Diagrama en bloques para estimación de velocidad en el rotor
3-31 Referencia de velocidad versus velocidad real rotor
3-32 Velocidad estimada
3-33 Numerador ecuación 3-50
3-34 Denominador ecuación 3-50
4-1Inversor alimentado en tensión de dos niveles
4-2 Ocho vectores en el plano complejo
4-3 Sector 1 hexágono inversor de 2
4-4 Patrón de conmutación para sector 1.
4-5 Algoritmo de modulación vectorial implementado en SIMULINK
4-6 Generación del vector de referencia
4-7 Cálculo del sector en que se encuentra el vector de referencia
4-8 Angulo del vector de referencia
4-9 Sector en que se encuentra el vector de referencia
4-10 Factor en común para los tiempos activos
14
4-11 Tiempos de activación
T1 , T2
generales
4-12 Tiempos de conmutación para S1 , S2 , S3 .
4-13 Tensión fase neutro inversor de dos niveles
4-14 Tensiones de línea del inversor
4-15 Análisis de Fourier para la tensión de fase neutro inversor
4-16 Análisis de Fourier tensión de fase con PWM sinusoidal
4-17 Inversor de tres niveles NPC
4-18 Niveles de Tensión
4-19 Vectores del inversor NPC en el plano complejo.
4-20 Sector uno hexágono pequeño
4-21 Sector uno hexágono mediano
4-22 Sector uno hexágono grande
4-23 Distribución estados de conmutación sector uno hexágono pequeño
4-24 Cálculo de los sectores
4-25 Tiempos T1 , T2 , T0
4-26 Tensión de referencia a la salida de un brazo del inversor
4-27 Tensión fase neutro del inversor NPC.
4-28 Tensión de línea para el inversor NPC
4-29 Serie de Fourier para triangular
4-30 Triangular en Mathcad.
4-31. Sinusoidales bases para moduladoras en Mathcad
4-32 Sinusoidales mas componentes en Mathcad
4-33 Moduladoras en Mathcad
4-34 Moduladora mas triangulares en Mathcad
4-35 Célula Monofásica
4-36 Modulación SVPWM en Bloques
4-37 Moduladoras en Simulink
4-38 Tensión a la salida célula monofásica
4-39 Implementación general en Simulink
4-40 Referencia de velocidad versus real
4-41 Corriente estator usando CSVPWM
4-42 Corriente estator usando SPWM
4-43 Corriente estator usando SVPWM
4-44 Corriente estator usando CSVPWM
INTRODUCCIÓN
El Control vectorial o también conocido como control por orientación de
campo FOC (Field Oriented Control) es uno de los métodos usados para realizar
el control de la magnitud como la fase del flujo magnético del motor asíncrono
para conseguir un funcionamiento análogo al del motor de corriente continua que
hasta hace algunos años era el motor más usado para los accionamientos de
velocidad variable [1].
Actualmente, como consecuencia de los importantes progresos en
electrónica de potencia y micro controladores, el control de una máquina de
inducción han tenido un gran desarrollo. El motor de inducción es conocido por
su robustez, bajo costo, fiabilidad, por lo que ha sido sujeto de varias
investigaciones. Sin embargo, ha sido por largo tiempo usado en aplicaciones
industriales que no requieren de un alto rendimiento. En cambio el motor de
corriente continua ha sido largamente usado en aplicaciones de velocidad
variable, donde el torque
y el flujo están naturalmente desacoplados y que
puede ser controlado independientemente, mediante sus corrientes de campo y
de armadura en el caso de una máquina de excitación independiente
Desde que Blashke y Hasse desarrollaron la nueva técnica de control
denominada control vectorial, el uso de la máquina de inducción se ha vuelto
más frecuente en operaciones que requieren un gran desempeño. Esta
estrategia de control entrega el mismo rendimiento que para un motor de
corriente continua de excitación independiente [2].
En este proyecto de titulo se comienza con un análisis de la aplicación de
las transformadas de Clark y Park para lograr una simplificación del análisis del
motor de inducción y su posterior aplicación en conjunto con el control vectorial.
Al finalizar todo el análisis teórico se procederá a simular en Matlab
Simulink el sistema estudiado, en donde se realizarán pruebas de carga,
variaciones en la referencia de velocidad, cambios de modulaciones para
obtener una visión general del comportamiento del motor de inducción.
2
CAPÍTULO 1
LAS TRANSFORMADAS DE CLARK Y PARK
1.1
TRANSFORMACIÓN DE CLARK
Esta transformación permite cambiar las variables de tensión, corriente y
flujo magnético, desde un sistema de referencia trifásico en movimiento a uno
bifásico estático. En general consiste en reemplazar el efecto del devanado
trifásico por otro bifásico formado por dos devanados “
”y “
” desfasados en
el espacio por 90 grados con el mismo factor de devanado, el número de espiras
del devanado bifásico debe ser equivalente al devanado trifásico.
Si consideramos una máquina asíncrona trifásica con tres devanados en
el estator “a”, “b”, “c” desfasados en el espacio 120 grados eléctricos con
Ns
espiras por polo por fase y factor de devanado “ k w ” que llevan respectivamente
las corrientes:
I A cos( t )
(1-1)
ib
I A cos( t 120 )
(1-2)
ic
I A cos( t 120 )
(1-3)
ia
Si consideramos que la distribución de la fuerza magnetomotriz es
senodal, para el caso producido por un devanado concentrado de paso
diametral, que se puede ver en la figura (1-1):
Fm
Figura 1-1 Devanado concentrado de paso diametral
3
Podemos ver en la figura, que las flechas negras muestran la distribución
sinusoidal de la fuerza magnetomotriz la cual será completamente definida si se
conoce su amplitud y la posición espacial del máximo positivo de la onda, este
segmento orientado en rojo representa el fasor espacial de la fuerza
magnetomotriz cuya distribución
espacial por la periferia del entrehierro la
describe la función cos( ) .
Por lo tanto la distribución de la fuerza magnetomotriz sinusoidal se puede
escribir:
Fm cos( )
Fm
Magnetomotriz ( )
(1-7)
Donde:
Fm
4* N * i
*2
(1-8)
Si la corriente que circula por el devanado concentrado de paso diametral
es:
i
(1-9)
I A cos( t )
Finalmente la fuerza magnetomotriz producida es:
(1-10)
F ( , t ) [ Fm cos( t )]cos( )
En nuestro caso la fuerza magnetomotriz generada por el devanado
trifásico debe ser proyectada sobre los ejes “
”y “
” como se observa en la
figura 1-2.
i
b
3N s
2
a
ia
c
b
ib
a
ic
c
b
3N s
2
a
c
i
Figura 1-2 Proyección sobre los ejes “
”y “
”.
4
De esta manera tenemos:
F
4
4
F
N s k w [ia sen ( ) ib sen(
120 ) ic sen(
120 )]
(1-11)
N s k w [ia cos( ) ib cos(
120 ) ic cos(
120 )]
(1-12)
3N s
espiras por polo y por fase y produce
2
En el devanado bifásico tiene
en los ejes “
”y “
” las fuerzas magnetomotriz siguiente:
F
4 3N s
kwi
2
(1-13)
F
4 3N s
kwi
2
(1-14)
Al igualar las fuerzas magnetomotrices se obtiene:
i
i
2
[ia sen( ) ib sen(
3
120 ) ic sen(
120 )]
(1-15)
2
[ia cos( ) ib cos(
3
120 ) ic cos(
120 )]
(1-16)
Estas ecuaciones representan los valores de las corrientes que deben
circular por el devanado bifásico para que produzcan las mismas fuerzas
magnetomotrices que el sistema trifásico.
Debemos agregar una tercera variable que no contribuya a la creación de
fuerzas magnetomotrices en el entrehierro, la tercera variable debe ser una
corriente homopolar o de secuencia cero i0 :
1
(ia ib ic )
3
i0
(1-17)
Además:
ia ib ic
0
(1-18)
Por lo tanto:
i0
0[ A]
(1-19)
5
En forma matricial tenemos:
i
sen( ) sen( 120 ) sen( 120 )
ia
2
cos( ) cos( 120 ) cos( 120 ) * ib
3
1
1
1
ic
2
2
2
i
i0
(1-20)
Donde la matriz de transformación es:
T
sen( ) sen( 120 ) sen( 120 )
2
cos( ) cos( 120 ) cos( 120 )
3
1
1
1
2
2
2
0
(1-21)
Esta es la matriz de Clarke la cual no solamente se aplica a las corrientes
del estator, también se aplica a los flujos y a las tensiones de estos devanados:
cos(
T
1
120 ) sen(
cos( )
0
cos(
120 ) 1
sen( )
120 ) sen (
1
120 ) 1
(1-22)
En el caso de que coincida el eje “ a ” del sistema trifásico con el eje “ ”
del bifásico,
0 por lo tanto las matrices de transformación anterior se
transforman en:
3
2
1
2
1
2
0
T
0
2
1
3
1
2
3
2
1
2
1
2
La transformada inversa queda expresada por:
1
3
1
2
2
1
0
1
T 01
1
2
3
2
1
(1-23)
(1-24)
6
1.2
TRANSFORMACIÓN DE PARK
Tenemos dos devanados fijos “
”y “
”, desfasados en el espacio por
90°, por los cuales circulan corrientes i , i respectivamente, se quiere sustituir
el efecto de estos devanados estáticos por otro conjunto de dos devanados “d” y
“q” situados entre sí a 90° pero que se muevan a velocidad
respecto del
primero. Ambos conjuntos deben producir la misma fuerza magnetomotriz en el
entrehierro de la máquina, considerando las corrientes anteriormente obtenidas:
i
(1-25)
I A * sen( 1t )
i
(1-26)
I A * cos( 1t )
Igualando las fuerzas magnetomotrices que producen ambos conjuntos de
devanados sobre los ejes “d” y “q” tal como se observa en la figura 1-3.
Por consiguiente la fuerza magnetomotriz generada por el devanado
bifásico proyectada sobre los ejes “d” y “q”:
Fq
N s (i cos( ) i cos( ))
(1-27)
Fd
N s (i sen ( ) i cos( ))
(1-28)
En el devanado bifásico estático tiene Ns espiras por polo y por fase y
produce en los ejes “d” y “q” las fuerzas magneto motriz siguiente:
Fq
N s * iq
(1-29)
Fd
N s * id
(1-30)
Ns
Ns
iq
i
Ns
Ns
i
id
0
Figura 1-3 Ejes d y q.
7
Igualando las fuerzas magnetomotrices obtenemos:
iq
i cos( ) i sen( )
(1-31)
id
i sen ( ) i cos( )
(1-32)
En forma matricial:
iq
sen( ) cos( )
id
cos( )
*
sen( )
i
i
(1-33)
La matriz de transformación sería:
T0
sen( ) cos( )
cos( ) sen( )
(1-34)
La matriz de transformación inversa sería
T0
1
sen ( ) cos( )
cos( ) sen( )
(1-35)
Podemos concluir que las corrientes en el sistema bifásico fijo varían con
respecto al tiempo, mientras que en el sistema móvil las corrientes son
constantes, como si fueran continuas, que dependen del ángulo inicial de giro, y
si consideráramos un desfase de la corriente inicial, también esta estaría
presente.
Si agregamos una tercera variable, debe ser una corriente homopolar o de
secuencia cero
i0 , la que será idéntica en los sistemas de referencia “
”y “
”y
“d” y “q”:
iq
sen( ) cos( ) 0
id
cos( )
i0
0
i
sen( ) 0 * i
0
1
(1-36)
i0
Si tenemos en cuenta la transformación de Clarke, se puede conseguir
una transformación que transforme un conjunto trifásico de devanados fijos a, b,
c situados en el estator, por un sistema bifásico móvil “d” y “q” que se mueve a
velocidad angular
respecto a una referencia fija.
8
Utilizando la transformada de Clark:
0
i
i
i0
2
3
1
3
3
3
1
3
1
3
3
3
ia
1
* ib
3
ic
1
3
(1-37)
Si reemplazamos la expresión (1-37) en (1-36), se obtiene la siguiente
matriz:
iq
id
cos( ) cos( 120 ) cos( 120 )
ia
2
sen( ) sen ( 120 ) sen( 120 ) * ib
3
1
1
1
i0
ic
2
2
2
(1-38)
La transformación correspondiente se denomina transformación de park,
donde
1t
0:
Tqd 0
cos( ) cos( 120 ) cos( 120 )
2
sen( ) sen( 120 ) sen( 120 )
3
1
1
1
2
2
2
(1-39)
Estas transformadas se usan para representar las variables sinusoidales
del sistema de coordenado trifásico en valores constantes, trayendo consigo
mayor estabilidad numérica al solucionar el sistema de ecuaciones diferenciales
no lineales, propias del modelo del motor de inducción.
9
CAPÍTULO 2
MODELO MATEMÁTICO MOTOR INDUCCIÓN JAULA DE ARDILLA
2.1
MODELO DE LA MÁQUINA EN MARCO DE REFERENCIA ARBITRARIO
El marco de referencia arbitrario está rotando a una velocidad
en
dirección a la rotación del rotor, la idea es llevar los ejes trifásicos del estator y
rotor a un marco de referencia arbitrario que gira a una velocidad
, tal como se
muestra en la figura 2-1.
Como observación podemos agregar que al utilizar el modelo de la
máquina en un marco de referencia arbitrario podemos obtener los marcos de
referencia estacionario y el marco de rotación sincrónica de la manera siguiente:
Marco de referencia estacionario:
0
Marco de referencia de rotación sincrónica:
e
La ecuación de transformación de los ejes a, b, c, a los ejes q, d, 0 está dada
por:
Donde la variable
f
fq
fa
fd
Tqd 0 ( ) * fb
f0
fc
(2-1)
puede ser: voltajes de fase, corrientes o enlaces de
flujo de la máquina.
r
Figura 2-1 Marco de referencia arbitrario que gira a una velocidad
,.
10
Si se considera que el rotor está referido al estator y además sabemos que:
Número de vueltas efectivas del estator: Ns
Número de vueltas efectivas del rotor: Nr
Se tiene que:
qr
Ns
Nr
qr
(2-2)
dr
Ns
Nr
dr
(2-3)
i
qr
Ns
iqr
Nr
(2-4)
i
dr
Ns
idr
Nr
(2-5)
L lr
Ns
Llr
Nr
(2-6)
R
Ns
Rr
Nr
(2-7)
r
Ecuaciones de voltaje del estator en ejes qd0:
vqs
Rs * iqs
d
dt
qs
*
ds
(2-8)
vds
Rs * ids
d
dt
ds
*
qs
(2-9)
v0 s
d
dt
Rs * i0 s
(2-10)
0s
Ecuaciones de voltaje del rotor en ejes qd0:
v
qr
Rr * i
qr
d
dt
qr
(
r
)*
dr
(2-11)
v
dr
Rr * i
dr
d
dt
dr
(
r
)*
qr
(2-12)
v
0r
Rr * i
0r
d
dt
0r
(2-13)
11
Ecuaciones de enlace de flujo para estator en ejes qd0:
qs
( Lls
Lm )* iqs
Lm * i
qr
(2-14)
ds
( Lls
Lm ) * ids
Lm * i
dr
(2-15)
Si
(2-16)
Lls * i0 s
0s
Lls
(2-17)
Ls Lm
qs
Ls * iqs
Lm * i
qr
(2-18)
ds
Ls * ids
Lm * i
dr
(2-19)
( Ls
0s
(2-20)
Lm ) * i0 s
Ecuaciones de enlace de flujo para rotor en ejes qd0:
qr
Lm * iqs ( L lr
Lm ) * i
qr
(2-21)
dr
Lm * ids
Lm ) * i
dr
(2-22)
L lr * i
0r
Si
( L lr
L lr
(2-23)
0r
Lr
(2-24)
Lm
qr
Lm * iqs
L r *i
qr
(2-25)
dr
Lm * ids
L r *i
dr
(2-26)
0r
(L r
Lm ) * i
(2-27)
0r
Ecuación para el torque en ejes qd0:
La suma de las potencias instantáneas de entrada de los 6 devanados
que conforman al rotor y estator está dado por:
Pin
vas * ias
vbs * ibs
vcs * ics
v
as
*i
qr
*i
as
v
bs
*i
dr
*i
bs
v
cs
*i
(2-28)
cs
En términos de los ejes qd0:
Pin
3
vqs * iqs vds * ids 2* v0 s * i0s v
2
qr
v
dr
2* v 0 r * i
0r
(2-29)
Si se sustituye en la expresión anterior las ecuaciones de voltaje de rotor y
estator en los ejes qd0, donde finalmente luego de agrupar los términos se
obtiene:
12
Rs * i 2 qs
Pin
3
2
d
dt
*
Rs * i 2 ds
qs
* iqs
ds
* iqs
d
dt
2* Rs * i 20 s
ds
*
d
dt
* ids
qs
* ids
2
Rr * i
0s
d
dt
* i0 s
(
r
)*
dr
2
Rr * i
qr
*i
qr
*i
d
dt
qr
(
qr
2
2* Rr * i
dr
dr
r
)*
0r
*i
qr
d
dt
qr
*i
0r
*i
0r
dr
(2-30)
Finalmente el torque electromecánico desarrollado por la maquina está
dado por la suma de las componentes que representan la cantidad de energía
convertida en trabajo mecánico dividida por la velocidad mecánica:
P
3
*
2 2*
Tem
ds
* iqs
qs
* ids
(
r
)
*i
dr
qr
qr
dr
(2-31)
* ids
(2-32)
*i
r
Usando las relaciones de enlace de flujo siguientes:
ds
* iqs
qs
* ids
dr
*i
qr
*i
qr
Lm
dr
dr
* iqs
qr
Obteniéndose finalmente el torque electromecánico en diferentes
expresiones equivalentes:
Tem
3 P
*
2 2
Tem
3 P
*
2 2
Tem
3 P
* * Lm i
2 2
Tem
3 P Lm
* *
2 2 Lr
qr
ds
*i
dr
dr
* iqs
qs
dr
*i
dr
(2-33)
qr
(2-33)
* ids
qs
*i
*i
qs
i
qr
*i
qr
(2-34)
ds
*i
ds
(2-35)
A menudo las ecuaciones de la máquina son expresadas en términos de
los enlaces de flujo por segundo y reactancias en vez de los enlaces de flujos e
inductancias. Estos están relacionados solamente por la base o el valor nominal
de la frecuencia angular
b
, entonces tenemos:
13
qs
b
*
qs
(2-36)
ds
b
*
ds
(2-37)
0s
b
*
0s
(2-38)
qr
b
dr
Con
b
b
(2-39)
qr
*
b
0r
*
(2-40)
dr
*
(2-41)
0r
qm
b
*
qm
(2-42)
dm
b
*
dm
(2-43)
como la frecuencia base en [Rad/s], además
b
* Lls
(2-44)
lr
b
* L lr
(2-45)
Xm
b
* Lm
(2-46)
X ls
X
Las tensiones quedan definidas de la siguiente manera:
Rs * iqs
vqs
Rs * ids
vds
v0 s
v
v
qr
dr
R r *i
R r *i
v
0r
1 d
b dt
qs
1 d
b dt
ds
Rr * i0 s
qr
dr
1 d
b dt
qr
1 d
b dt
dr
0r
(2-47)
qs
(2-48)
b
1 d
b dt
R r *i
ds
b
(2-49)
0s
(
r
)
dr
(2-50)
qr
(2-51)
b
(
r
)
b
1 d
b dt
0r
52)
14
Circuito equivalente en ejes qd0, se observa en la figura 2-2:
X ls
*
X
i
(
r
ds
b
R
qr
lr
)
*
r
dr
b
Xm
qs
v
qr
v
dr
qr
Eje Q
X
X ls
*
i
dr
R
lr
(
r
qs
)
*
r
qr
b
b
Xm
ds
dr
Eje D
Figura 2-2 Circuito equivalente en ejes qd0.
Las expresiones de flujo quedan expresadas como:
qs
X s * iqs
X m *i
qr
(2-53)
ds
X s * ids
X m *i
dr
(2-54)
0s
X ls * i0 s
(2-55)
qr
X r *i
qr
X m * iqs
(2-56)
dr
X
dr
X m * ids
(2-57)
0r
X
r
*i
lr
*i
(2-58)
0r
qm
X m (iqs i qr )
(2-59)
dm
X m (ids
(2-60)
i
dr
)
Las corrientes pueden ser expresadas en términos de los flujos:
15
qs
iqs
qm
qr
i
qr
qm
(2-62)
X lr
ds
ids
i
(2-61)
X ls
(2-63)
dm
X ls
dr
dr
dm
(2-64)
X lr
Donde:
qm
X ml
dm
X ml
qs
qr
X ls
(2-65)
X lr
ds
dr
X ls
(2-66)
X lr
Con:
X ml
1
1
X ls
1
Xm
(2-67)
1
X lr
Podemos volver a escribir las ecuaciones de tensión, reemplazando las
componentes de corrientes por los flujos obtenidos:
vqs
vds
v
v
qr
dr
Rs
*(
X ls
qs
Rs
*(
X ls
ds
R
X
R
X
r
*(
qr
qm
)
dm
qm
)
)
lr
r
lr
*(
dr
dm
)
1 d
b dt
qs
1 d
b dt
ds
(2-68)
qs
(2-69)
b
b
1 d
b dt
qr
1 d
b dt
dr
Obtendremos las ecuaciones siguientes:
ds
(
r
)
dr
(2-70)
qr
(2-71)
b
(
r
b
)
16
d
qs
b
dt
d
ds
b
d
rs
X ls
qs
X ml
X ls
vds
qs
rs
X ls
ds
X ml
1
X ls
b
qr
b
dt
ds
b
dt
d
vqs
b
dt
X ml dr
X lr
(2-73)
qr
X ml
1
X lr
(2-74)
qr
rr X ml ds
X lr
X ls
dr
X ml
X lr
(2-75)
r
vdr
(2-72)
rr X ml qs
X lr
X ls
b
dr
qr
X lr
dr
r
vqr
X ml
1
b
1
Finalmente el torque electromagnético lo podemos escribir de la siguiente
manera:
Tem
2.2
3 P Xm 1
* *
*
2 2 X r
b
dr
*i
qs
qr
*i
ds
(2-76)
PARÁMETROS DEL MOTOR DE INDUCCIÓN
Se decidió ocupar un motor trifásico de inducción conectado en estrella
con los siguientes parámetros referidos al estator:
Tabla 2-1
Especificaciones
Parámetros
Potencia Nominal
3000[W]
Rs
0.19[Ohm]
Voltaje Nominal
220[V]
Rr
0.39[Ohm]
Corriente Nominal
6.6[A]
Lls
0.21[mH]
Frecuencia Nominal 50[Hz]
Llr
0.6[mH]
Numero de Polos
4
Lm
4[mH]
Velocidad nominal
1430[RPM] J
0.0226[Kgm^2]
Torque Nominal
20[N-m]
0.002[Nms/rad]
B
17
2.3
ANÁLISIS MATEMÁTICO
Las tensiones trifásicas en ejes de cuadratura y directo en un marco
sincrónico son las siguientes:
Utilizando la transformación de Clark obtenemos lo siguiente:
VsQ
VsD
2
3
0
1
3
1
3
1
Va
3
* Vb
1
Vc
3
Además sabemos que Va Vb Vc
(2-77)
0 porque el sistema es balanceado.
Luego se realiza una transformada de Park para llevar el sistema a un eje
de coordenadas sincrónico:
Tensión del estator en el eje de cuadratura:
VsQ
220
0 [V ]
3
(2-78)
Tensión del estator en el eje directo:
VsD
220
90 [V ]
3
(2-79)
Como último paso se aplica la transformación de Park:
Vsq
Vsd
V
sen ( )
cos( )
* sQ
VsD
sen ( ) cos( )
(2-80)
Tensión del estator en el eje de cuadratura en marco sincrónico:
Vsq
0[V ]
(2-81)
Tensión del estator en el eje directo en marco sincrónico:
Vsd
220* 2
[V ]
3
(2-82)
Ordenando las ecuaciones que relacionan tensión y corriente en ejes d - q
en un marco sincrónico para el motor de inducción se obtiene la siguiente
expresión matricial:
18
Rs
d
dt
Ls
Vsq
Vsd
e Ls
Vrq
Vrd
d
Lm
dt
(
e
r
Ls
s
Rs
(
) Lm
d
dt
e Lm
) Lm
d
Lr
dt
Ls
e
r
Lm
d
dt
Lm
Rr
d
dt
(
e
r
(
) Lr
e
Lm
Lm
d
dt
e
r
Rr
Lr
*
) Lr
isq
isd
irq
ird
(2-83)
d
dt
En base a los resultados obtenidos en (2-81)-(2-82) procedemos a
calcular las corrientes, los enlaces de flujo, en ejes d - q para el estator y el rotor
en base a su funcionamiento a parámetros nominales
Las tensiones en eje de cuadratura y directo son valores constantes, por
lo tanto:
d
isq
dt
d
isd
dt
d
irq
dt
d
ird
dt
0
(2-84)
La expresión (2-83) queda reducida a:
Vsq
Vsd
Vrq
Vrd
Rs
e Ls
0
(
e
r
0
Ls
Rs
e
(
) Lm
e
r
e
) Lm
0
Lm
0
Lm
Rr
(
isq
i
* sd
irq
r ) Lr
Rr
ird
e
e
(
r
) Lr
e
(2-85)
Corrientes en el estator y rotor:
isq
133.32[ A]
isd
19.38[ A]
irq
0.027[ A]
ird
0.19[ A]
(2-86)
Flujos en el estator:
qs
qs
0.56[Wb]
(2-87)
0.08[Wb]
(2-88)
b
ds
ds
b
19
Flujos en el rotor:
qr
0.53[Wb ]
(2-89)
0.076[Wb ]
(2-90)
qr
b
dr
dr
b
Torque electromagnético:
Tem
2.4
3 P Lm
* *
2 2 Lr
dr
*i
qs
qr
*i
ds
0[ N
m]
(2-91)
SIMULACIONES EN MATLAB SIMULINK.
Las ecuaciones que representan el comportamiento dinámico del motor de
inducción son implementadas en bloques utilizando la herramienta de MATLAB –
SIMULINK.
En la figura 2-3 se aprecia el desarrollo en bloques de la ecuación (2-72).
En la Figura 2-4 se aprecia el desarrollo en bloques de la ecuación (2-73).
En la Figura 2-5 se aprecia el desarrollo en bloques de la ecuación (2-74).
En la Figura 2-6 se aprecia el desarrollo en bloques de la ecuación (2-75).
En la Figura 2-7 se aprecia el desarrollo en bloques de la ecuación (2-65).
En la figura 2-8 se aprecia el desarrollo en bloques de la ecuación (2-66).
En la Figura 2-9 se aprecia el desarrollo en bloques de la ecuación (2-61).
En la Figura 2-10 se aprecia el desarrollo en bloques de la ecuación (263).
En la Figura 2-11 se aprecia el desarrollo en bloques de la ecuación (262).
En la Figura 2-12 se aprecia el desarrollo en bloques de la ecuación (264).
En la Figura 2-13 se aprecia el desarrollo en bloques de la ecuación (276).
En la Figura 2-14 se aprecia el desarrollo en bloques de la ecuación (320).
20
En la Figura 2-15 se aprecian todos los bloques anteriormente
desarrollados unidos entre si para formar el modelo matemático completo del
motor de inducción.
En la Figura 2-16 se aprecia la transformada de Clark desarrollada en
bloques.
En la Figura 2-17 se aprecia la transformada de Park desarrollada en
bloques.
En la Figura 2-18 se aprecia el sistema completo desarrollado en bloques.
Se debe recordar que en este punto no se utiliza inversor, dado que las
tensiones de alimentación para el motor de inducción son sinusoidales puras a
50Hz.
A continuación se procede a simular el motor de inducción en condiciones
nominales de operación.
En la Figura 2-19 se aprecia la tensión
vsd , vsq a la salida de la
transformada de Park.
Se obtienen en estado estacionario los siguientes resultados:
Vsq
Vsd
0[V ]
(2-92)
179.6[V ]
(2-93)
En la Figura 2-20 se aprecian las tensiones sinusoidales en el estator.
En la Figura 2-21 se aprecian las corrientes sinusoidales del estator.
En la Figura 2-22 se aprecia la velocidad sincrónica en verde que
corresponde a 1500[RPM] y en azul a la variación en la velocidad mecánica del
rotor.
Se obtienen en estado estacionario los siguientes resultados:
rmech
s
1499.32[ RPM ]
(2-94)
1500[ RPM ]
(2-95)
En la Figura 2-23 se aprecia la corriente
isq .
Se obtienen en estado estacionario el siguiente resultado:
21
isq
133[ A]
En la Figura 2-24 se aprecia la corriente
(2-96)
isd .
Se obtienen en estado estacionario el siguiente resultado:
isd
19.29[ A]
En la Figura 2-25 se aprecia la corriente
(2-97)
irq .
Se obtienen en estado estacionario el siguiente resultado:
irq
0.027[ A]
En la Figura 2-26 se aprecia la corriente
(2-98)
ird .
Se obtienen en estado estacionario el siguiente resultado:
ird
0.1928[ A]
En la Figura 2-27 se aprecia el enlace de flujo
(2-99)
qs
.
Se obtienen en estado estacionario el siguiente resultado:
qs
0.56[Wb]
En la Figura 2-28 se aprecia el flujo enlazado
(2-100)
ds
.
Se obtienen en estado estacionario el siguiente resultado:
ds
0.08[Wb]
En la Figura 2-29 se aprecia el flujo enlazado
(2-101)
qr
.
Se obtienen en estado estacionario el siguiente resultado:
qr
0.5322[Wb]
En la Figura 2-30 se aprecia el enlace de flujo
(2-102)
dr
.
Se obtienen en estado estacionario el siguiente resultado:
dr
0.076[Wb]
(2-103)
22
Figura 2-3 Ecuación para flujo
qs
Figura 2-4 Ecuación para flujo
ds
Figura 2-5 Ecuación para flujo
qr
23
Figura 2-6 Ecuación para flujo
dr
Figura 2-7 Ecuación para flujo
mq
Figura 2-8 Ecuación para flujo
md
Figura 2-9 Ecuación para la corriente isq
24
Figura 2-10 Ecuación para la corriente isd
Figura 2-11 Ecuación para la corriente irq
Figura 2-12 Ecuación para la corriente ird
Figura 2-13 Ecuación para el torque Te
25
Figura 2-14 Ecuación para la velocidad
r
Figura 2-15 Modelo completo motor de inducción.
Figura 2-16 Ecuación de la transformada de Clark.
26
Figura 2-17 Ecuación de la transformada de Park
Figura 2-18 Sistema completo motor de inducción.
Figura 2-19 Tensión vsd , vsq .
27
Figura 2-20 Tensiones sinusoidales en el estator.
Figura 2-21Corrientes sinusoidales del estator.
Figura 2-22 Velocidad sincrónica y velocidad mecánica en el rotor.
28
Figura 2-23 Corriente
isq .
Figura 2-24 Corriente
isd .
Figura 2-25 Corriente
irq
29
Figura 2-26 Corriente
ird
Figura 2-27 Flujo enlazado estator eje q
qs
Figura 2-28 Flujo enlazado estator eje d
ds
30
Figura 2-29 Flujo enlazado rotor eje q
qr
Figura 2-30 Flujo enlazado rotor eje d
dr
31
CAPÍTULO 3
EL CONTROL VECTORIAL
3.1
INTRODUCCIÓN AL CONTROL VECTORIAL
En el control vectorial, la máquina de inducción se controla igual que una
máquina de corriente continua de excitación independiente, en las figura 3-1 se
aprecia el esquema de control de una máquina de corriente continua
El flujo es controlado por la corriente de campo, en donde la corriente de
campo es habitualmente constante, el torque es controlado por la corriente de
armadura.
La idea principal del control vectorial es controlar una máquina de
corriente alterna de igual forma que una máquina de corriente continua, lo que
significa controlar separadamente el flujo y el torque del motor.
3.2
CONTROL DE CAMPO ORIENTADO
En una máquina de corriente continua los ejes de la armadura y el
bobinado de campo son ortogonales, la fuerza magnetomotriz establecida por
las corrientes en estos devanados son también ortogonales y la saturación del
hierro es ignorada:
Figura 3-1 Máquina de corriente continua de excitación independiente.
32
El torque desarrollado queda definido por:
Tem
ka ( I f ) I a
(3-1)
ka : Coeficiente de proporcionalidad. Convino
I a : Corriente de armadura.
If
: Corriente de campo.
(I f )
: Flujo de campo.
El flujo puede ser controlado ajustando la corriente de campo y el torque
puede ser controlado independientemente del flujo ajustando la corriente de
armadura.
El control vectorial de un motor de inducción permite mejorar su respuesta
dinámica, aproximándola a la del motor de corriente continua, esta técnica de
control exige disponer de un buen modelo del motor a controlar, el control
vectorial desacopla las variables del motor de inducción, por lo tanto se consigue
un control independiente de velocidad y torque, equiparables a la sencillez en el
control de una máquina CC.
Marco de referencia de rotación sincrónica: (
e
)
Si nosotros tenemos una excitación sinusoidal, el campo del rotor gira a
velocidad sincrónica, si elegimos un marco qd0 que gire a velocidad sincrónica
donde el eje d es alineado con el campo del rotor, la componente de campo del
e
rotor
qr
será cero:
e
Lm * i e qs
qr
i
e
Si
qr
0
e
qr
L r *i
e
qr
0
Lm e
i qs
Lr
(3-2)
(3-3)
el torque electromagnético se reduce a:
Tem
Si sustituimos
i
3 P
*
2 2
e
dr
*i
e
qr
e
qr
en la ecuación de torque electromagnético:
(3-4)
33
3 P Lm
* *
2 2 Lr
Tem
e
* i e qs
dr
(3-5)
e
Lo que muestra que si mantenemos constante
dr
el torque puede ser
e
independientemente controlado ajustando la componente i qs del eje q.
e
Si
d
qr se mantiene en cero, la variación dt
e
qr
es igual a cero tenemos
que la ecuación en el eje q de la tensión en el bobinado del rotor, sin tensión
aplicada al rotor se reduce a:
v
e
R r *i
qr
qr
R r *i
0
d
dt
e
e
e
qr
(
qr
(
e
r
)*
e
r
e
)*
(3-6)
dr
e
(3-7)
dr
En otras palabras la velocidad de deslizamiento debe satisfacer:
(
e
r
e
R r *i
)
qr
e
(3-8)
dr
e
También si consideramos que
d
constante), dt
no varía en el tiempo (se mantiene
dr
e
dr
e
es cero, considerando la condición anterior y que
qr
0
en
la ecuación de voltaje en el eje d, obtendremos:
v
e
R r *i
dr
e
dr
d
dt
R r *i
La componente
i
e
0
dr
e
(
dr
e
e
r
)*
e
qr
0
dr
(3-9)
(3-10)
, entonces:
Lm * i e ds
dr
e
e
L r *i
e
dr
Lm * i e ds
dr
(3-11)
(3-12)
Sustituyendo en la expresión para la velocidad de deslizamiento:
(
e
r)
R r *i
e
dr
e
qr
(3-13)
34
e
dr
i
Lm * i e ds
(3-14)
Lm e
i qs
Lr
(3-15)
e
qr
Finalmente obtenemos la siguiente relación entre la velocidad de
deslizamiento y la razón entre las componentes de corriente del estator en ejes
“d” y “q” para que el eje “d” del marco de referencia sincrónico quede alineado
con el campo del rotor, como se observa en la figura 3-2.
(
e
r)
R r *i
e
qs
L r * i eds
(3-16)
En la figura 3-2 podemos ver que las corrientes del estator se
descomponen en una componente proporcional al flujo
torque
isd
y otra proporcional al
isq , que corresponden a las componentes de corrientes en un sistema de
coordenadas rotatorio, las cuales son ortogonales entre si, lo que permite un
control independiente de ambas componentes de corriente, lo más importante es
identificar la posición del flujo para poder expresar al vector de corriente con
respecto al eje “d” rotatorio orientado en la dirección del flujo, por esta razón
también recibe el nombre de método de control de flujo orientado al rotor.
Con
isq controlamos el torque y con isd controlamos el flujo, el cual debe
ser mantenido constante.
Donde
es el Angulo de flujo de rotor, el cual es calculado directamente
desde el motor en base a la velocidad de deslizamiento y la velocidad del rotor.
e
isq
rd
is
r
isd
slip
r
Figura 3-2 Marco de referencia sincrónico alineado con el campo del rotor.
35
3.3
MODELO DE CONTROL A UTILIZAR
El método de control es el indirecto por fuente de tensión, en el cual se
realimentan las corrientes en el estator y la referencia entregada es la velocidad
requerida para el rotor, en la figura 3-3 podemos ver el esquema general para
realizar el control indirecto por fuente de tensión.
3.4
DEFINICIÓN DE LAS PLANTAS PARA LAZOS DE CONTROL
Para definir los lazos de control primero se deben determinar las
respectivas ecuaciones de plantas de cada una de las variables a controlar,
luego se definirá el tipo de controlador más apropiado, que debe ser utilizado
para controlar cada variable en particular, según los requerimientos que de ellas
se deseen obtener.
De las ecuaciones que describen la dinámica del motor tenemos las
siguientes ecuaciones en un marco de referencia sincrónico:
disd
dt
Rs
* Ls
1
*
isd
e
Lm
* Ls * Lr *
* isq
r
rd
r
Lm * r
* Ls * Lr *
rq
r
1
vsd
* Ls
(3-17)
d
rd
Lm
dt
*
isd
rd
r
e
r
rq
(3-18)
r
Te*
r
1
isq *
Vqq
Vq *
Vd *
r
*
dr
isd
Vdd
*
e
isq
isd
r
Figura 3-3 Método de control indirecto por fuente de tensión
36
d
Lm
rq
dt
1
isq
e
rd
rq
r
(3-19)
r
3* p 2 * Lm
isq
2 * 2 2 * J * Lr
d r
dt
r
1
r
isd
rd
B
J
rq
r
p
TL
2* J
(3-20)
Lm 2
Ls * Lr
(3-21)
Lr
Rr
(3-22)
Pero al estar en el marco de referencia de campo orientado las
ecuaciones anteriores se transforman en:
disd
dt
Rs
* Ls
disd
dt
1
*
Rs
* Ls
isd
e
r
1
isq
*
r
d
rd
dt
d r
dt
Lm
* Ls * Lr *
* isq
3* p 2 * Lm
isq
2 * 2 2 * J * Lr
e
Lm
r
Lm * r
* Ls * Lr
* isd
rd
1
Vsd
* Ls
1
Vsq
* Ls
(3-23)
(3-24)
1
isd
rd
r
rd
rd
(3-25)
r
B
J
r
p
TL
2* J
(3-26)
En base a estas ecuaciones diferenciales podemos modelar nuestras
plantas en un marco de referencia de campo orientado, por
lo tanto
obtendremos cuatro plantas, dos de corriente, una para el flujo y una para la
velocidad:
3.4.1 Plantas de corriente
Desarrollando las ecuaciones (3-23) y (3-24) de corriente, obtendremos:
37
Rs * iqs
diqs
Ls
Rs * ids
Vsq
dt
Ls
dids
dt
Vsd
Vqq Vsq
Vdd
Ls
Vsd
Ls
Ls
Lm
Lr
e
i
e ds
(3-27)
Lm
Lr
e
i
e qs
Lm
Lr
dr
Lm
Lr
qr
qr
(3-28)
e
i
e ds
Ls
dr
(3-29)
e
i
e qs
(3-30)
Dos plantas para las corrientes del estator en ejes de cuadratura y directo,
las cuales serán idénticas y estarán dadas por:
ids
Vdd
iqs
1
Ls S Rs
Vqq
(3-31)
En donde finalmente se le deben sumar las siguientes componentes para
lograr el desacople de tensión:
Vsq
Vqq
Ls eids
Vsd
Vdd
Ls eiqs
Lm
Lr
e
dr
(3-33)
3.4.2 Planta de velocidad
Desarrollando la ecuación (3-26) de velocidad, obtendremos:
d r
dt
3* p 2 * Lm
isq
2 * 2 2 * J * Lr
2* J d r
p dt
B
J
rd
3* p * Lm
isq
2 2 * Lr
2* J d r
p dt
2* B
p
rd
r
r
2* B
p
p
TL
2* J
r
(3-34)
TL
(3-35)
Tres
(3-36)
38
r
2* J
S
p
2* B
p
Tres
(3-37)
Finalmente obtenemos la ecuación de planta para el control de velocidad:
p
r
2
Tres JS B
(3-38)
3.4.3 Planta de flujo
Desarrollando la ecuación (3-25) de flujo, obtendremos:
d rd
dt
Lm
d
1
rd
r
rd
Lm
r
S
(3-39)
r
rd
dt
rd
1
isd
isd
(3-40)
r
1
Lm
r
r
isd
(3-41)
Finalmente obtenemos la ecuación de planta para el control de velocidad:
Lm
rd
isd
r
S
1
(3-42)
r
3.5
DISEÑO DE LOS CONTROLADORES APLICADOS
3.5.1 Controlador PI de corriente
El método utilizado para sintonizar los cuatro controladores PI es el de
asignación de polos y ceros, en donde se asigna un polo en el origen y un cero
en -500 para cada uno de los controladores. Estos fueron simulados con la
39
herramienta RLTOOL la cual permite una sintonización manual y en tiempo real
de la ganancia integral y proporcional.
En base a esta planta se diseñara un controlador proporcional integral con
las siguientes características:
Tiempo de asentamiento: 0.00632[s]
Tiempo de subida:0.000137[s]
Sobrepaso: 6.49% (1.06)
El controlador es el siguiente:
Corrientecontrolador
0.84933( S 500)
S
(3-43)
La respuesta al escalón unitario en lazo cerrado en la figura 3-4.
3.5.2 Controlador PI de flujo
En base a esta planta se diseñara un controlador proporcional integral con
las siguientes características:
Tiempo de asentamiento: 0.00602[s]
Tiempo de subida:0.000973[s]
Sobrepaso: 12.7% (1.13)
El controlador es el siguiente:
Flujocontrolador
4332.7089( S 500)
S
(3-44)
La respuesta al escalón unitario en lazo cerrado en figura 3-5.
3.5.3 Controlador PI de velocidad
En base a esta planta se diseñara un controlador proporcional integral con
las siguientes características:
Tiempo de asentamiento: 0.00553[s]
Tiempo de subida:0.000768[s]
40
Sobrepaso: 14.2% (1.42)
El controlador es el siguiente:
Velocidad controlador
10.5499( S 500)
S
(3-45)
La respuesta al escalón unitario en lazo cerrado en la figura 3-6.
3.5.4 Controlador PI mas antiarrollamiento (Antiwindup)
Todo sistema a controlar tiene límites de saturación, en los casos en
donde la referencia entregada supera la saturación, la componente integral de la
saturación sigue sumando el error generado del sistema al querer superar la
saturación. Si al cabo de un tiempo la referencia se sitúa bajo esta saturación el
sistema tendrá una demora en volver a seguir la referencia, porque deberá
contrarrestar la suma generada anteriormente al superar la saturación.
Por lo tanto para evitar este problema se agrega a los controladores PI el
sistema de antiarrollamiento, este en el momento que la saturación es superada
por la referencia, el antiarrollamiento elimina la parte integral del controlador,
evitando la suma del error generado.
En la figura 3-7 podemos ver un sistema controlador PI, saturación y
función de transferencia de planta, en donde no se ocupa el sistema con
antiarrollamiento:
En la figura 3-8 tenemos la respuesta en verde, se aprecia que hay un
atraso n seguir la referencia en azul.
En cambio en la figura 3-9 podemos ver el controlador PI más anti
arrollamiento:
Podemos ver en la figura 3-10 que la respuesta en verde se acopla
inmediatamente a la referencia proporcionada cuando se disminuye del valor de
saturación:
41
3.6
SIMULACIÓN CONTROL VECTORIAL EN MATLAB-SIMULINK
En primera instancia se realizara la simulación del modelo propuesto en
condición de vacío del motor de inducción, en la figura 3-11 podemos ver el
modelo a simular en forma general:
3.6.1 Simulación a torque constante
En primer lugar veremos la respuesta del motor de inducción a la
referencia de velocidad en la figura 3-12, aquí se aprecia en verde la respuesta
en rad/s del motor frente a la referencia que queda sobrepuesta por la respuesta
del motor, las variaciones de velocidad contemplan desde 0rad/s hasta 950rad/s
que corresponde a 3 veces la velocidad sincrónica del motor de inducción en
vacío.
En la figura 3-13 se aprecia la tensión de fase en el estator del motor de
inducción trifásico, se notan claramente los 2 niveles de tensión que proporciona
el inversor trifásico puente completo.
En la figura 3-14 se aprecia la tensión línea a línea en el estator del motor
de inducción trifásico, se notan claramente los 3 niveles de tensión que
proporciona el inversor trifásico puente completo.
En la figura 3-15 se aprecia el torque electromagnético del motor, se
aprecian ciertas variaciones que corresponden a los cambios de velocidad dados
en la referencia, notándose con especial detalle el torque negativo en la
pendiente de desaceleración que ocurre entre los 6 y los 6.5 segundos de
simulación:
En la figura 3-16 se aprecia la corriente en el eje de cuadratura del
estator, entre los segundos 6 y 6.5:
En la figura 3-17 se tiene el flujo en el eje directo del rotor, apenas la
velocidad del motor supera la velocidad sincrónica, el flujo se va debilitando de
forma inversamente proporcional a la velocidad del rotor en cambio, cuando la
42
velocidad del motor es inferior a la sincrónica el flujo es constante e igual al flujo
nominal del motor.
En la figura 3-18 se ve la corriente trifásica en el estator en referencia a la
velocidad del motor, para apreciar sus cambios de amplitud y frecuencia.
En la figura 3-19 se aprecia la corriente trifásica en el estator realizando
un zoom, para poder apreciar su forma sinusoidal.
En la figura 3-20 se ve la corriente en el eje directo del estator, esta es
responsable del flujo en el eje directo del rotor en marco de referencia de campo
orientado,
en el tiempo 6 a 6.5 segundo podemos ver que esta aumenta,
produciendo un aumento en el flujo del rotor, lo que produce una disminución en
la velocidad que es inversamente proporcional al torque.
Finalmente en la figura 3-21 se aprecia el comportamiento en verde de la
velocidad angular del campo en el motor en rad/s y en azul la velocidad en rad/s
del motor de inducción, se aprecia como la velocidad del campo supera la
velocidad del motor, esto se produce gracias a cómo va variando la frecuencia
de la tensión que impone el inversor en el motor de inducción.
3.6.2 Simulación del sistema a velocidad y torque variable
En segunda instancia se realizara la simulación del modelo propuesto
variando el torque en la carga y la velocidad, en la figura 3-22 se puede ver en
rojo el torque en la carga y en verde la velocidad de referencia y sobre ella la
respuesta de velocidad del motor, se aprecia una correcta respuesta del motor
frente a los cambios dinámicos de velocidad y torque.
En la figura 3-23 se aprecia el torque electromecánico que responde
perfectamente a la carga impuesta en el motor de inducción.
En la figura 3-24 se aprecia como la corriente trifásica en el estator va
ajustándose a los requerimientos de carga del motor, esta variación en su
amplitud es proporcional al torque demandado.
43
En la figura 3-25 se realizó un zoom a las corrientes trifásicas para ver su
comportamiento sinusoidal.
En la figura 3-26 se aprecia la corriente en el eje de cuadratura que influye
directamente en el toque electromagnético del motor, torque es proporcional a la
corriente en el eje de cuadratura del estator.
En la figura 3-27 la corriente en el eje directo del estator que se mantiene
constante porque en todo momento se trabajó bajo la velocidad sincrónica,
entonces el flujo en el eje directo del rotor es constante.
En la figura 3-28 se tiene la velocidad angular del campo en el estator en
verde y la velocidad angular del rotor en azul ambas en rad/s, se aprecia que en
todo momento la velocidad angular del campo en el estator es mayor que la del
rotor.
En la figura 3-29 se puede ver el flujo en el eje directo del rotor, el cual es
constante por estar trabajando en el intervalo sub sincrónico.
3.7
CONTROL VECTORIAL SIN SENSOR DE POSICIONAMIENTO
Actualmente se están desarrollando aplicaciones de control vectorial sin la
necesidad de estar continuamente muestreando la posición del rotor, mediante
diferentes algoritmos podemos obtener de manera aproximada la velocidad
mecánica del rotor, a continuación se realizaran simulaciones del sistema en
lazo abierto para determinar la velocidad estimada del rotor, se desprecian los
efectos de la saturación, temperatura y efectos al operar en bajas frecuencias.
En base a las ecuaciones de la dinámica del motor de inducción en un
marco de referencia arbitrario, llevándolas a un marco de referencia estacionario
(
0 ), inicialmente se deben obtener las componentes en eje directo y de
cuadratura del flujo en el estator en un marco de referencia con respecto al
estator, por lo tanto se obtiene:
sD
vsD
Rs isD dt
(3-46)
44
vsQ
sQ
(3-47)
Rs isQ dt
Relacionando las ecuaciones (2-18), (2-19), (2-25) y (2-26) se obtiene:
rd
Lr
Lm
sD
Ls isD
(3-48)
rq
Lr
Lm
sQ
Ls isQ
(3-49)
Relacionando (2-12) con (2-26), se obtiene:
dr
tr
Lmids
tr
d
dr
dt
r
(3-50)
qr
Por lo tanto se puede proceder desarrollar las ecuaciones anteriores en
base al programa de simulación obteniéndose (Figura 3-30):
De esta manera, incorporando esta técnica para estimar la velocidad del
rotor al sistema de control vectorial en la lazo cerrado obtenemos las siguientes
respuestas:
En la Figura 3-40 se puede ver en verde la referencia de velocidad
mecánica en RPM y en azul la respuesta del motor:
En la figura 3-41 se puede ver la velocidad eléctrica estimada del rotor en
radianes segundo que corresponde a la ecuación 3-50
En la figura 3-41 se puede ver diferentes impulsos que no afectan la
respuesta del sistema, tal cual como se puede ver en la figura 3-40.
Esto ocurre porque el nominador y denominador de la ecuación son
señales sinusoidales sin offset en torno a cero, por lo tanto en cada uno de los
momentos que el denominador se aproxima a cero la velocidad eléctrica
estimada del rotor tiende a ser infinita, sin embargo estar perturbaciones no
afectan al sistema de control vectorial.
En la figura 3-42 se tiene la forma de onda correspondiente a como varia
numerador y la figura 3-43 la del denominador de la ecuación 3-50.
45
Figura 3-4 Respuesta al escalón unitario planta de corriente
Figura 3-5 Respuesta al escalón unitario planta de flujo
46
Figura 3-6 Respuesta al escalón unitario planta de velocidad
Figura 3-7 Controlador PI
Figura 3-8 Respuesta del controlador PI
47
Figura 3-9 Controlador PI con Antiarrollamiento
Figura 3-10 Respuesta del controlador PI con Antiarrollamiento
Figura 3-11 Modelo general control vectorial aplicado al motor de inducción
48
Figura 3-12 Respuesta del motor de inducción a la referencia de velocidad
Figura 3-13 Tensión de fase neutro inversor de dos niveles.
Figura 3-14 Tensión de línea de tres niveles
49
Figura 3-15 Torque electromagnético del motor
Figura 3-16 Corriente en el eje de cuadratura del estator
Figura 3-17 Flujo en el eje directo del rotor
50
Figura 3-18 Corriente trifásica en el estator en referencia a la velocidad del motor
Figura 3-19 Corriente trifásica en el estator
Figura 3-20 Corriente en el eje directo del estator
51
Figura 3-21 Velocidad angular del campo en el estator
Figura 3-22 Variación de torque en la carga y de velocidad
Figura 3-23 Torque electromecánico
52
Figura 3-24 Variación de la corriente en el estator en función de la carga
Figura 3-25 Corrientes trifásicas en el estator.
Figura 3-26 Corriente en el eje de cuadratura del estator
53
Figura 3-27 Corriente en el eje directo del estator
Figura 3-28 Velocidad angular del campo
Figura 3-29 Flujo en el eje directo del rotor
54
Figura 3-30 Diagrama en bloques para estimación de velocidad en el rotor
Figura 3-31 Referencia de velocidad versus velocidad real rotor
Figura 3-32 Velocidad estimada
Figura 3-33 Numerador ecuación 3-50
55
Figura 3-34 Denominador ecuación 3-50.
56
CAPÍTULO 4
EL ALGORITMO DE MODULACIÓN VECTORIAL
4.1
MODULACIÓN VECTORIAL.
La modulación PWM vectorial es una técnica avanzada de síntesis de
tensiones a la salida de un inversor, la cual consiste en generar un espacio
vectorial en un plano complejo, en donde cada uno de sus vectores representa
un estado de conmutación especifico del inversor utilizado, esta modulación
puede ser utilizada desde el inversor alimentado en tensión de dos niveles hasta
un inversor multinivel.
La modulación PWM vectorial en comparación con la modulación de PWM
sinusoidal permite un buen control del sistema, además permite establecer
estrategias de minimización de pérdidas, menor contenido armónico y la
atenuación de la tensión en modo común.
En esta tesis el objetivo es asimilar el algoritmo de modulación vectorial
para su futura aplicación en inversores multinivel, de esta manera se comenzará
el estudio por los inversores de dos y tres niveles para poder extrapolar la
técnica a un inversor de 5 niveles o más.
4.2
ALGORITMO DE MODULACIÓN
INVERSOR DE DOS NIVELES.
VECTORIAL
APLICADA
A
UN
Si se utiliza un inversor alimentado en tensión de dos niveles, se puede
ver que este tiene 8 estados de conmutación, que está dado por su cantidad de
niveles y la cantidad de brazos que posee figura 4-1:
Cantidad de estados de conmutación permitidos:
23
8
(4-1)
57
Figura 4-1Inversor trifásico alimentado en tensión de dos niveles
Para comenzar el análisis para la implementación de la modulación
vectorial se debe considerar lo siguiente:
Se consideran los tres interruptores superiores para cada brazo, dado que
los inferiores son el complemento de los superiores.
Para cada estado permitido de conmutación se realiza un análisis equivalente de
malla para determinar las tensiones fase neutro inversor y fase neutro carga.
Los resultados obtenidos para el análisis de malla para cada uno de los estados
de conmutación permitidos se aprecian en la tabla 1.
58
Tabla 4-1
V.N°
S1
S3
S5
Vao
Vbo
Vco
Van
Vbn
Vcn
0
0
0
0
0
0
0
0
0
0
1
1
0
0
E/2
-E/2
-E/2
2E/3
-E/3
-E/3
2
1
1
0
E/2
E/2
-E/2
2E/3
2E/3
-E/3
3
0
1
0
-E/2
E/2
-E/2
-E/3
2E/3
-E/3
4
0
1
1
-E/2
E/2
E/2
-E/3
2E/3
2E/3
5
0
0
1
-E/2
-E/2
E/2
-E/3
-E/3
2E/3
6
1
0
1
E/2
-E/2
E/2
2E/3
-E/3
2E/3
7
1
1
1
0
0
0
0
0
0
Mediante la transformada a un plano complejo (4-2) podemos representar
cada uno de los estados permitidos por un único vector, con magnitud y ángulo
fijos:
V
2
j
2
vas (t ) vbs (t )e 3
3
vcs (t )e
j
4
3
(4-2)
En la tabla 4-2 se aprecian los ocho estados de conmutación
representados de forma vectorial.
Finalmente cada uno de estos vectores son llevados al plano complejo
bidimensional que se muestra en la figura 4-2.
Cada vector de amplitud
2E
forma un vértice del hexágono de la figura 43
2, estos seis vectores se llamaran vectores activos y los dos restantes de
amplitud 0 se llamaran vectores nulos.
Cada región formada estará compuesta por la interacción de dos vectores
activos y los dos nulos, estas regiones estarán separadas por 60 grados cada
una.
59
Dado que las 6 regiones son idénticas se centrara todo el análisis en una
de las regiones, la región 1 de la figura 4-2.
Tabla 4-2
V.N° Magnitud, Angulo[Rad]
0
Nulo
1
2E / 3, 0
2
2E / 3, / 3
3
2E / 3, 2 / 3
4
2E / 3,
5
2E / 3, 2 / 3
6
2E / 3,
/3
7
Nulo
010
b
110
60o
a
011
100
111
000
001
c
101
Figura 4-2 Ocho vectores en el plano complejo
En la figura 4-3 se aprecia el sector 1 aislado para realizar su análisis
matemático.
Como condición inicial siempre tendremos la magnitud y la posición del
vector de referencia y las magnitudes de los vectores activos pertenecientes al
sector:
Descomponiendo cada vector para visualizar el aporte a los ejes
" "," " obtenemos:
0 V2 sen(60 )T2
Vs Ts sen( )
(4-3)
60
V1T1 V2 cos(60 )T2
Despejando
T1 , T2
Ts Vs
sen(60
VDC
)
2
3
Ts Vs
2
sen( )
VDC
3
T2
T1 , T2
(4-4)
se obtiene:
T1
En donde
Vs Ts cos( )
(4-5)
(4-6)
son los tiempos de activación de sus respectivos vectores
activos.
VDC
V2
VS
V0 V7
V1 VDC
Figura 4-3 Sector 1 hexágono inversor de 2 niveles
Por lo tanto el vector de referencia quedaría definido por:
VS
T1
T
T
V1 2 V2 0 V0
TS
TS
TS
(4-7)
TS
(4-8)
T0 T1 T2
En la ecuación (4-7) se aprecia la importancia de los vectores nulos que
permiten variar la amplitud del vector de referencia.
Dado que los seis sectores son idénticos se procede a generalizar las
ecuaciones para calcular los
activos de cada sector:
T1 , T2
correspondientes a cada par de vectores
61
3 * TS * Vs
n
sin
VDC
3
T1
T2
3 * TS * Vs
VDC
En donde: 0
sin
n 1
3
cos
cos
n
3
cos
cos
n 1
3
(4-9)
sin
sin
(4-10)
60 o .
Finalmente se debe entregar un patrón de conmutación tal que la cantidad
de conmutaciones en un periodo de conmutación sean mínimas, la forma de
lograr esto es fijando los vectores nulos en el centro y en los costados del
periodo de conmutación, a esto se le debe el nombre de modulación vectorial por
vectores espaciales centrados, el patrón para el sector uno se puede ver en la
figura 4-4.
Figura 4-4 Patrón de conmutación para sector 1.
En donde los tiempos de conmutación para los interruptores superiores
S1, S2 y S3 quedan definidos de la siguiente manera:
S1 T1 T2 T0 / 2
S2 T2 T0 / 2
S3
T0 / 2
(4-11)
(4-12)
(4-13)
62
De esta misma manera se definen los tiempos de conmutación para cada
uno de los demás cinco sectores
En resumen la técnica de modulación vectorial queda determinada por:
Primer paso: Generar plano
" "," "
en base a los estados de
conmutación.
Segundo paso: Teniendo como dato inicial el vector de referencia y las
magnitudes de los vectores activos determinar
T1 , T2 , T0 .
Tercer paso: Ordenar los estados de conmutación para cada sector para
una mínima cantidad de conmutaciones y obtener los tiempos de conmutación
de cada interruptor.
4.3
ALGORITMO IMPLEMENTADO EN MATLAB – SIMULINK.
En la figura 4-5 se aprecia de forma general el algoritmo de modulación
vectorial implementado en MATLAB – SIMULINK.
Figura 4-5 Algoritmo de modulación vectorial implementado en SIMULINK
63
En la figura 4-6 se aprecian los bloques para la generación del vector de
referencia deseado, se fija la amplitud máxima de:
Vs max
1
*VDC
3
146.64[V ]
(4-14)
Figura 4-6 Generación del vector de referencia
Figura 4-7 Calculo del sector en que se encuentra el vector de referencia
Rescatando el Angulo del vector de referencia se procede a calcular en
que sector del hexágono se encuentra, figura 4-7.
Mediante la división entera del ángulo y un ciclo entero obtenemos como
varía el ángulo entre 0 y 2
[rad] obteniéndose la gráfica de la figura 4-8.
Luego esta se divide por los 60 grados, se redondea al entero menor y se
suma uno a la forma de onda resultante, obteniéndose el sector en el que se
encuentra el vector de referencia, figura 4-9.
64
Figura 4-8 Angulo del vector de referencia
Figura 4-9 Sector en que se encuentra el vector de referencia
Para todos los tiempos activos tenemos un factor en común que queda
representado en bloques como se aprecia en la figura 4-10 y el factor común es
representado en la ecuación (4-15).
FactorComun
3 * TS * Vs
VDC
(4-15)
En la figura 4-11 se encuentran las ecuaciones (4-9)-(4-10) que
representan los tiempos
T1 , T2
de manera general para todos los sectores.
En la figura 4-12 quedan expresados los tiempos de activación para los
tres interruptores superiores del inversor de dos niveles dependiendo del sector
en que se encuentre.
65
Figura 4-10 Factor en común para los tiempos activos
Figura 4-11Tiempos de activación
T1 , T2
generales
Figura 4-12 Tiempos de conmutación para
S1 , S2 , S3 .
En la figura 4-13 se aprecia la tensión fase a neutro de cada uno de los
brazos del inversor, las cuales son de dos niveles.
En la figura 4-14 se aprecian las tres tensiones de línea del inversor, se
aprecian los 3 niveles de tensión.
66
Figura 4-13 Tensión fase a neutro del inversor de dos niveles
Figura 4-14 Tensiones de línea del inversor
Figura 4-15 Análisis de Fourier para la tensión de fase a neutro del inversor
En la figura 4-15 se aprecia el análisis de Fourier para la tensión de fase
neutro inversor, la cual tiene una amplitud de la fundamental a 50Hz de 254[V]
con un THDv=52.24%.
67
Figura 4-16 Análisis de Fourier tensión de fase con PWM sinusoidal
Figura 4-17 Inversor de tres niveles NPC
En la figura 4-16 se aprecia el análisis de Fourier para la misma tensión
de fase neutro inversor pero aplicándose PWM sinusoidal, se aprecia que la
componente fundamental tiene una amplitud de 219.9[V] y un THDv de 68.46%
Al comprar ambas modulaciones se aprecia claramente que la Modulación
vectorial logra una mayor amplitud en la componente fundamental y una menor
distorsión armónica en la tensión de fase neutro inversor.
68
4.4
ALGORITMO DE MODULACIÓN VECTORIAL PARA UN INVERSOR
NPC DE TRES NIVELES DE TENSIÓN.
El inversor de tres niveles NPC (Neutral Point Clamped) figura 4-17 esta
compuesto de tres brazos en los cuales hay cuatro interruptores para ser
accionados en alta frecuencia, este inversor tiene 27 estados permitidos de
conmutación dados por la ecuación (4-16).
N iv e le s
fa s e s
33
27
(4-16)
Figura 4-18
La tensión de fase neutro inversor tiene la siguiente característica dada
por la figura 4-18, en donde se aprecian 3 niveles de tensión.
Al analizar cada uno de los estados de conmutación mediante un análisis
de malla para determinar las tensiones fase neutro inversor y fase neutro carga
se obtienen 24 vectores activos y 3 vectores nulos en donde tenemos 12
vectores de magnitud E/3 que se aprecian en la tabla 4-3.
En la tabla 4-4 se puede ver los siguientes vectores activos de amplitud
E 3
y los vectores activos de amplitud 2E/3.
3
Mediante la transformación para llevar componentes trifásicas ec.(4-2)
obtenemos el siguiente plano complejo figura 4-19, de esta manera quedan
ubicados 3 vectores nulos y 24 vectores activos.
69
Figura 4-19 Vectores del inversor NPC en el plano complejo.
Figura 4-20 Sector uno hexágono pequeño
Por lo tanto tenemos tres Hexágonos los cuales tienen seis sectores cada
uno, por lo tanto debemos calcular cada uno de los T1 y T2 para cada uno de los
sectores de cada hexágono.
En primer lugar se analiza el hexágono interior:
Se obtiene las siguientes ecuaciones para los tiempos activos del sector
1:
T1
Ts Vs
sen(60
E
T2
)
Ts Vs
6
sen( )
E
3
6
3
(4-17)
(4-18)
70
Para el hexágono mediano se tiene el sector 1 en la figura 4-21, se
obtienen las siguientes ecuaciones para los tiempos activos en el sector 1 del
hexágono mediano:
T1
Ts Vs
2*3
cos( )
E
3* 3
Ts Vs
sen(
E
T2
30 )
2*3
3* 3
(4-19)
(4-20)
Figura 4-21 Sector uno hexágono mediano
Figura 4-22 Sector uno hexágono grande
Para el hexágono grande, el sector uno en la figura 4-22, se obtienen los
siguientes tiempos de activación para el sector uno del hexágono mayor:
T1
Ts Vs
sen(60
E
)
3
3
(4-21)
71
T2
Ts Vs
3
sen( )
E
3
(4-22)
En consecuencia se procede a calcular los tiempos de conmutación para
el par de interruptores superiores del hexágono uno menor, para este caso
tenemos las siguientes posibilidades de conmutación para el sector uno, en
donde se aprecian tres vectores nulos y dos pares de vectores redundantes:
Respetando que la cantidad de conmutaciones en un periodo de
conmutación debe ser la mínima se distribuyen los estados de conmutación de
tal manera que queden centrados los vectores nulos, para este caso el patrón de
conmutación es el que se aprecia en la figura 4-23.
Figura 4-23 Distribución estados de conmutación sector uno hexágono pequeño
Por lo tanto los tiempos de conmutación para el sector uno del hexágono
pequeño son:
Sa1 T5 T7 T0
Sa 2
T4 T6 T0 T5 T7
Sb1 T7 T0
Sb 2
T6 T0 T5 T7 T0
(4-23)
(4-24)
(4-25)
(4-26)
72
Sc1 T0
Sc 2
T0 T5 T7 T0
(4-27)
(4-28)
Finalmente se realiza el mismo procedimiento para los sectores restantes
de cada hexágono y se procede a implementar el algoritmo en MATLABSIMULINK, este procedimiento se aprecia en detalle en el anexo A.
4.5
ALGORITMO IMPLEMENTADO EN MATLAB SIMULINK PARA UN
INVERSOR NPC ALIMENTADO EN TENSIÓN.
En la figura 4-24 se tiene la gráfica resultante del cálculo de los sectores,
se aprecian los 6 sectores desfasados en 60 grados cada uno.
Figura 4-24 Cálculo de los sectores
Figura 4-25 Tiempos
T1 , T2 , T0 .
73
Figura 4-26 Tensión de referencia a la salida de un brazo del inversor
En la figura 4-25 se tiene la gráfica de los tiempos de activación
T1 , T2 , T0 .
En la figura 4-26 se tiene en azul la tensión de referencia que deseamos a
la salida del inversor, se aprecia que posee las componentes de tercera
armónica, esta debe ser llevada a la frecuencia de conmutación restándole una
portadora triangular a la frecuencia de conmutación.
En la figura 4-27 se tiene la tensión fase a neutro del inversor de tres
niveles de tensión.
En la figura 4-28 se tiene la tensión de línea para el inversor, se aprecian
los 5 niveles de tensión.
Figura 4-27 Tensión fase a neutro del inversor NPC.
74
Figura 4-28 Tensión de línea para el inversor NPC.
4.6
NUEVOS ALGORITMOS
INVERSORES MULTINIVEL
DE
MODULACIÓN
VECTORIAL
PARA
4.6.1 Algoritmo de modulación vectorial CSV-PWM
La modulación por ancho de pulso centrada por vectores espaciales
(CSV-PWM) [6] es una alternativa al algoritmo anteriormente planteado, esta
consiste en tener un arreglo de N-1 señales portadoras de igual magnitud, fase y
frecuencia, que ocupan en bandas contiguas todo el rango de modulación lineal,
donde N representa el número de niveles de tensión que posee el inversor, en
general es un arreglo se señales analógicas.
Las señales de referencia son superpuestas sobre el conjunto de señales
portadoras, y el punto de intersección de ambas señales, determina el nivel de
tensión en salida que deben tener los interruptores, para cada ciclo de transición
o estado de funcionamiento.
La modulación por disposición de fase puede ser extendida a CSV-PWM,
por la suma de un offset que contiene la componente de tercera armónica, y está
definida por:
V k'
Vk
[m ax (V a , V b , V c )
m in (V a , V b , V c )]
2
,k
a, b, c
(4-29)
75
Además de una función modulo que identifica cual de las señales de
referencia es la responsable para la primera y última transición del interruptor en
cada intervalo, y es dada por:
Vk''
[V k'
V DC ] mod
2 V DC
N 1
(4-30)
La ecuación antes presentada se utiliza porque en los inversores de
múltiples niveles, se necesita identificar cual señal de referencia es la
responsable del inicio en la secuencia de los vectores que están presentes en
cada medio periodo de la señal portadora.
Finalmente la señal de referencia que incorpora los offset, queda defina
por la siguiente ecuación:
VR EF _ k
4.6.2 Obtención
matemática
V
'
k
VDC
4
de las
[m ax(V a'' , V b'' , V c'' )
m in(V a'' , V b'' , V c'' )]
2
señales
de referencia mediante
(4-31)
programación
Mediante la utilización de las ecuaciones descritas anteriormente se
pretende obtener en forma empírica, las señales de referencia para cada fase.
Utilizando el programa de simulación matemática MATHCAD se obtiene la
portadora triangular, en términos de su amplitud y periodo (figura 4-29).
Vp
f1 (t )
f 2 (t )
T
T
2
2
Figura 4-29 Serie de Fourier para triangular.
El periodo es inversamente proporcional al índice de frecuencia deseado:
76
2
mf
T
(4-32)
mf
0
(4-33)
La triangular está formada por dos rectas, las cuales se dan a
continuación sus ecuaciones correspondientes:
0,V p
(4-34)
,0
(4-35)
y1
( x x1 )
x1
(4-36)
,0
mf
0,Vp
y
mf
y2
x2
y1
m f Vpt
f1 (t )
f 2 (t ) V p
(4-37)
Vp
m f V pt
(4-38)
Luego la serie de Fourier está definida por:
a0
2
f (t )
an cos( n 0t )
n 1
bn sen( n 0t )
(4-39)
n 1
Donde los coeficientes de Fourier están definidos por:
a0
an
bn
2
T
2
T
T
2
T
2
2
T
T
2
T
2
f (t )dt
(4-40)
f (t ) cos(n 0t )dt
(4-41)
f (t ) sen(n 0t )dt
(4-42)
T
2
T
2
Evaluando las integrales obtenemos los valores de cada uno de los
coeficientes:
a0
2
T
T
2
T
2
f (t )dt
mf
0
mf
m f Vp t
V p dt
mf
0
Vp
m f V pt
dt
(4-43)
77
a0 Vp
an
2
T
T
2
T
2
mf
f (t ) cos( n 0t )dt
0
(4-44)
m f Vp t
V p cos( n 0t )dt
mf
mf
0
Vp
m f V pt
cos( n 0t )dt
(4-45)
2Vp cos(n ) 1
an
n2
T
2
T
2
2
T
bn
(4-46)
2
(4-47)
f (t ) sen(n 0t )dt
bn
0
(4-48)
Finalmente la serie de Fourier de la triangular propuesta es:
f (t )
Vp
2
2Vp cos(n ) 1
n 1
n2
2
cos(nm f t )
(4-49)
La grafica de la ecuación 4-49 se aprecia en la Figura 4-30.
1
0.8
0.6
trig ( t )
0.4
0.2
0
2
0
2
t
Figura 4-30 Triangular en Mathcad
Las señales de referencia para las moduladoras se aprecian en la Figura
4-31, las cuales son las ecuaciones 4-50, 4-51, 4-52.
va ( t ) sin( t )
(4-50)
vb ( t ) sin( t
2
)
3
(4-51)
vc ( t ) sin( t
2
)
3
(4-52)
78
Ahora procedemos a hacer la evaluación de todos los offset anteriormente
mencionados Figura 4-32:
max va ( t ), vb ( t ), vc ( t )
va1 ( t ) va ( t )
min va ( t ), vb ( t ), vc ( t )
2
max va ( t ), vb ( t ), vc ( t )
vb1 ( t ) vb ( t )
min va ( t ), vb ( t ), vc ( t )
2
max va ( t ), vb ( t ), vc ( t )
vc1 ( t ) vc ( t )
min va ( t ), vb ( t ), vc ( t )
2
(4-53)
(4-54)
(4-55)
1
va ( t )
vb( t ) 0
vc( t )
1
0
2
4
6
t
Figura 4-31. Sinusoidales bases para moduladoras en Mathcad.
1
0.5
va1( t )
vb1 ( t )
0
vc1( t )
0.5
1
0
2
4
6
t
Figura 4-32 Sinusoidales más componentes en Mathcad.
Finalmente obtenemos las moduladoras en la Figura 4-33:
vrefa ( t ) va1 ( t )
max va 2 ( t ), vb 2 ( t ), vc 2 ( t )
min va 2 ( t ), vb 2 ( t ), vc 2 ( t )
2
1
4
(4-56)
79
vrefb ( t )
vb1 ( t )
max va 2 ( t ), vb 2 ( t ), vc 2 ( t )
min va 2 ( t ), vb 2 ( t ), vc 2 ( t )
2
1
4
(4-57)
vrefc ( t ) vc1 ( t )
max va 2 ( t ), vb 2 ( t ), vc 2 ( t )
min va 2 ( t ), vb 2 ( t ), vc 2 ( t )
2
1
4
(4-58)
1
0.5
vrefa ( t )
vrefb ( t )
0
vrefc ( t )
0.5
1
0
2
4
6
t
Figura 4-33 Moduladoras en Mathcad.
Para completar la modulación debemos comparar las señales anteriores con las
portadores triangulares (Figura 4-30) desfasadas por amplitud, si usamos un
índice de frecuencia de 36 y una amplitud 1:
v p (V p , t )
Vp
200
2
n 1
2 * V p * (cos( n ) 1)
n2 *
2
cos( n * m f * t )
(4-59)
Además se superpone la señal moduladora y se obtiene la grafica de la
Figura 4-34.
vrefa ( t )
mi * va1 ( t )
max va 2 ( t ), vb 2 ( t ), vc 2 ( t )
min va 2 ( t ), vb 2 ( t ), vc 2 ( t )
2
1
4
(4-60)
80
1
0.5
vrefa ( t )
vp ( 0.5
t ) 0.5
vp ( 0.5
t)
vp ( 0.5
t ) 0.5
vp ( 0.5
t) 1
0
0.5
1
0
2
4
6
t
Figura 4-34 Moduladora mas triangulares en Mathcad.
4.7
APLICACIÓN DE LA CSV-PWM EN UN INVERSOR MULTINIVEL
4.7.1 Inversor multinivel hibrido simétrico
Se realiza una breve descripción del inversor multinivel hibrido simétrico
desarrollado en el laboratorio de electrónica de potencia, el cual será utilizado
para realizar el control vectorial del motor de inducción.
Se muestra la célula monofásica y su configuración trifásica, este inversor
se puede ver en más detalle en el trabajo de magister de Reynaldo Ramos [5],
en donde el muestra la “Familia de inversores multinivel híbridos para aplicación
en alta tensión y alta potencia”.
En la Figura 4-35 se muestra la topología de la célula monofásica.
Figura 4-35 Célula Monofasica.
81
Se aprecia que esta es alimentada por dos fuentes de tensión idénticas de
valor E,
S1 , S2 , S3 , S4
son interruptores rápidos bidireccionales en corriente, los
cuales pueden ser MOSFET o IGBT, estos soportan una tensión inversa máxima
de E y trabajan a una frecuencia desde aproximadamente 1Khz hacia arriba,
dado que estos interruptores pueden trabajar en altas frecuencias, estos
habitualmente soportan una menor tensión, estos interruptores son accionados
con PWM sinusoidal,
S5 , S6 , S7 , S8
son interruptores lentos bidireccionales en
corriente, los cuales pueden ser GTO o IGCT, estos soportan una tensión
inversa máxima de 2E y trabajan a una frecuencia menor que está dada por la
frecuencia de salida deseada (Habitualmente 50Hz), estos interruptores son
accionados por pulsos únicos.
Los interruptores lentos están distribuidos como puente H, los cuales
definen si la salida del inversor X – Y se encuentra en intervalo positivo o
negativo.
4.7.2 Implementación en simulink CSV-PWM
En la Figura 4-36 se tiene la modulación CSV-PWM desarrollada en
bloques en SIMULINK.
Figura 4-36 Modulación SVPWM en Bloques.
82
En la figura 4-37 se puede ver las moduladoras obtenidas idénticas a las
desarrolladas en el modelo matemático de la figura 4-34.
Figura 4-37 Moduladoras en Simulink.
En la figura 4-38 se puede ver la tensión fase neutro inversor de cinco
niveles de tensión.
Figura 4-38 Tensión a la salida célula monofásica.
4.7.3 Aplicación del control vectorial mas modulación CSV-PWM con un
inversor multinivel hibrido simétrico
En la figura 4-39 se puede ver el sistema simulado en su totalidad en
SIMULINK.
83
Figura 4-39 Implementación general en Simulink.
Figura 4-40 Referencia de velocidad versus real.
En la figura 4-40 se puede ver como la velocidad del motor sigue en todo
momento a la referencia deseada.
En la figura 4-41 se puede ver las corrientes trifásicas en el estator.
84
Figura 4-41 Corriente estator usando CSVPWM
4.7.4 Comparación de las corrientes en el estator con diferentes modulaciones
e inversores.
En la figura 4-42 se tiene la corriente en el estator de un motor de
inducción alimentado con un inversor de dos niveles con modulación S-PWM.
Figura 4-42 Corriente estator usando SPWM
En la figura 4-43 se tiene la corriente en el estator de un motor de
inducción alimentado con un inversor de dos niveles con modulación SV-PWM.
En la figura 4-44 se tiene la corriente en el estator de un motor de
inducción alimentado con un inversor multinivel hibrido simétrico con modulación
CSV-PWM
85
Figura 4-43 Corriente estator usando SVPWM
Figura 4-44 Corriente estator usando CSVPWM
Se puede ver en la figura 4-44 como la corriente es completamente
sinusoidal y con una notable menor distorsión que en los casos en donde se
ocupa el inversor de dos niveles.
86
Tabla 4-3 Doce vectores de magnitud E/3
Sa1
Sa2
Sb1
Sb2
Sc1
Sc2
Vao
Vbo
Vco
Van
Vbn
Vcn
Vsxo
V1
0
0
0
0
0
0
-E/2
-E/2
-E/2
0
0
0
-------
V2
1
1
1
1
1
1
E/2
E/2
E/2
0
0
0
-------
V3
0
1
0
1
0
1
0
0
0
0
0
0
-------
V4
0
1
0
0
0
0
0
-E/2
-E/2
E/3
-E/6
-E/6
E/3
0
V5
1
1
0
1
0
1
E/2
0
0
E/3
-E/6
-E/6
E/3
0
V6
0
1
0
1
0
0
0
0
-E/2
E/6
E/6
-E/3
E/3
/3
V7
1
1
1
1
0
1
E/2
E/2
0
E/6
E/6
-E/3
E/3
/3
V8
0
0
0
1
0
0
-E/2
0
-E/2
-E/6
E/3
-E/6
E/3
2 /3
V9
0
1
1
1
0
1
0
E/2
0
-E/6
E/3
-E/6
E/3
2 /3
V10
0
0
0
1
0
1
-E/2
0
0
-E/3
E/6
E/6
E/3
V11
0
1
1
1
1
1
0
E/2
E/2
-E/3
E/6
E/6
E/3
V12
0
0
0
0
0
1
-E/2
-E/2
0
-E/6
-E/6
E/3
E/3
2 /3
V13
0
1
0
1
1
1
0
0
E/2
E/6
-E/6
E/3
E/3
2 /3
V14
0
1
0
0
0
1
0
-E/2
0
E/6
-E/3
E/6
E/3
/3
V15
1
1
0
1
1
1
E/2
0
E/2
E/6
-E/3
E/6
E/3
/3
87
Tabla 4-4 vectores de amplitud
E 3
y de amplitud 2E/3
3
Sa
1
1
Sa
2
1
Sb1
Sb2
Sc1
Sc2
Vao
Vbo
Vco
Van
Vbn
Vcn
0
1
0
0
E/2
0
- E/2
E/2
0
- E/2
E 3
3
/6
V1
7
0
1
1
1
0
0
0
-E/2
- E/2
0
E/2
- E/2
E 3
3
/2
V1
8
0
0
1
1
0
1
- E/2
E/2
0
- E/2
E/2
0
E 3
3
5 /6
V1
9
0
0
0
1
1
1
- E/2
0
E/2
- E/2
0
E/2
E 3
3
5 /6
V2
0
0
1
0
0
1
1
0
- E/2
E/2
0
- E/2
E/2
E 3
3
/2
V2
1
1
1
0
0
0
1
E/2
E/2
0
E/2
- E/2
0
E 3
3
/6
V2
2
1
1
0
0
0
0
E/2
-E/2
-E/2
2E/3
-E/3
-E/3
2E/3
V2
3
1
1
1
1
0
0
E/2
E/2
-E/2
E/3
E/3
-2E/3
2E/3
/3
V2
4
0
0
1
1
0
0
-E/2
E/2
-E/2
-E/3
2E/3
-E/3
2E/3
2 /3
V2
5
0
0
1
1
1
1
-E/2
E/2
E/2
-2E/3
E/3
E/3
2E/3
V2
6
0
0
0
0
1
1
-E/2
-E/2
E/2
-E/3
-E/3
2E/3
2E/3
2 /3
V2
7
1
1
0
0
1
1
E/2
-E/2
E/2
E/3
-2E/3
E/3
2E/3
/3
V1
6
Vsxo
0
88
CONCLUSIONES
En primera instancia se logró simular el motor de inducción en base a las
ecuaciones
dinámicas
del
mismo,
ayudando
a
comprender
mejor
el
comportamiento del motor bajo condiciones de simulación en lazo abierto y
cerrado, además esto entrega una opción adicional al motor entregado por
MATLAB-SIMULINK.
En segunda instancia se pudo apreciar que en base al control vectorial se
puede controlar el motor de inducción a semejanza de un motor de corriente
continua de excitación independiente, logrando velocidades de por lo menos 3
veces la velocidad sincrónica en condiciones de vacío, abriendo las puertas de
aplicaciones de alta velocidad a bajo torque.
En tercera instancia se aprecia la estabilidad frente a cambios dinámicos
en la velocidad y torque en el motor de inducción, sin embargo debemos
recordar que al ser el torque inversamente proporcional a la velocidad, no
debemos sobre exigir el motor por sobre de sus límites de potencia, porque la
potencia en el motor de inducción es proporcional a la velocidad y el torque.
La modulación de inversores multinivel puede llevarse a cabo de dos
maneras, mediante PWM sinusoidal que es muy simple de implementar pero que
no entrega óptimos resultados, mientras que la modulación vectorial permite un
buen control del sistema, además los vectores redundantes permiten establecer
estrategias de minimización de perdidas, menor contenido armónico y la
atenuación de la tensión en modo común.
Se demuestra mediante un cambio de referencia en el marco de
referencia arbitrario como se puede diferenciar rápidamente las variables para
realizar un control sin sensor de posicionamiento, esto simplificaría notablemente
la implementación real de este sistema, manteniendo el mismo buen desempeño
que con el uso del sensor de posicionamiento.
89
BIBLIOGRAFÍA
[1] Peter Vas, Sensorless vector and direct torque control, Oxford University
Press, 1998.
[2] Chee Mung Ong, Dynamic Simulations of Electric Machinery, Prentice Hall,
1998.
[3] Krause, Wasynczuk, Sudhoff, Analysis of electric machinery and drive
systems, IEEE press, Second Edition, 2002.
[4] Karanayil, MF Rahman and C Grantham, “A complete dynamic model for
PWM VSI-fed rotor flux oriented vector controlled induction motor drive using
SIMULINK” School of electrical engineering and telecommunications, University
of New South Wales, Australia.
[5] Reynaldo Ramos A, Tesis de Magíster Familia de Inversores Multinivel
Híbridos para Aplicaciones en Alta Tensión y Alta Potencia, capitulo 5 Inversor
multinivel Híbrido trifásico basado en el IH1 FB-CT.
[6] B.P:McGrath, D.G.Holmes, and T. Meynard, “Reduce PWM Harmonic
Distortion for Multilevel Inverters Operating Over a Wide Modulation Range”,
IEEE Trans. Power. Electron.,Vol 21,NO. 4, July 2006.
[7] A. Laoufi, A. Hazzab, I. K. Bousserhane, M. Rahli, “Direct Field-Oriented
Control using Back stepping Technique for Induction Motor Speed Control”,
International Journal of Applied Engineering Research, ISSN 0973-4562 Vol.1
No.1 (2006) pp. 37-50.
90
APÉNDICE A
TIEMPOS DE CONMUTACIÓN PARA INVERSOR NPC EN EL CAPÍTULO 4
91
APÉNDICE A
TIEMPOS DE CONMUTACIÓN
Hexágono interior
Sector 1:
Se aprecia en la figura A-1 la distribución de los tiempos de conmutación para
los interruptores superiores del inversor NPC.
Sa1= T5 + T7 + T0/2
Sa2= T4 + T6 + T0+T0/2 + T5 + T7
Sb1= T7 +T0/2
Sb2= T6 + T0 + T5 + T7 + T0/2
Sc1= T0/2
Sc2= T0 + T5 + T7 + T0/2
Sector 2:
Se aprecia en la figura A-2 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T7 + T0/2
Sa2= T6 + T0 + T9 + T7 + T0/2
92
Sb1= T9 + T7 + T0
Sb2=T8 + T6 + T0 + T9 + T7 + T0/2
Sc1= T0/2
Sc2= T0 + T9 + T7 + T0/2
Sector 3:
Se aprecia en la figura A-3 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T0/2
Sa2= T0 + T9 + T11 + T0/2
Sb1= T9+ T11 + T0/2
Sb2= T8 + T10 + T0 + T9 + T11 + T0/2
Sc1= T11 + T0/2
Sc2= T10 + T0 + T9 + T11 + T0/2
Sector 4:
Se aprecia en la figura A-4 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T0/2
Sa2= T0 + T12 + T11 + T0/2
Sb1=T4 + T0/2
93
Sb2= T10 + T0 + T13 + T11 + T0/2
Sc1= T13 + T11 + T0/2
Sc2= T12 + T10 + T0 + T13 + T11 + T0/2
Sector 5:
Se aprecia en la figura A-5 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T15 + T0/2
Sa2= T14 + T0 + T13 + T15 + T0/2
Sb1= T0/2
Sb2= T0 + T13 + T15 + T0/2
Sc1= T13 + T15 + T0/2
Sc2= T12 + T14 + T0 + T13 + T15 + T0/2
Sector 6:
Se aprecia en la figura A-6 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
SA1= T5 + T15 + T0/2
SA2= T4 +T14 +T0 +T5 +T15 +T0/2
SB1= T0/2
SB2= T0 + T5 + T15 + T0/2
94
SC1= T15 + T0/2
SC2= T14 + T0 + T5 + T15 + T0/2
Hexagono mediano:
Sector 1:
Se aprecia en la figura A-7 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T16 + T0/2
Sa2= T17 + T0 + T16 + T0/2
Sb1= T17 + T0/2
Sb2= T17 + T0 + T16 + T0/2
Sc1= T0/2
Sc2= T0 + T0/2
Sector 2:
Se aprecia en la figura A-8 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T0/2
Sa2= T0 + T17 + T0/2
Sb1= T18 + T17 + T0/2
Sb2= T18 + T0 + T17 + T0/2
95
Sc1= T0/2
Sc2= T18 + T0 + T0/2
Sector3:
Se aprecia en la figura A-9 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T0/2
Sa2= T0 + T0/2
Sb1= T18 + T0/2
Sb2= T19 + T0 + T18 + T0/2
Sc1= T19 + T0/2
Sc2= T19 + T0 + T18 + T0/2
Sector 4:
Se aprecia en la figura A-10 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T0/2
Sa2= T20 + T0 + T0/2
Sb1= T0/2
Sb2= T0 + T19 + T0/2
Sc1= T20 + T19 + T0/2
96
Sc2= T20 + T0 + T19 + T0/2
Sector 5:
Se aprecia en la figura A-11 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T21 + T0/2
Sa2= T21 + T0 + T20 + T0/2
Sb1= T0/2
Sb2= T0 + T0/2
Sc1= T20 + T0/2
Sc2= T21 + T0 +T20 +T0/2
Sector 6:
Se aprecia en la figura A-12 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T16 + T21 + T0/2
Sa2= T16 + T0 + T21 + T0/2
Sb1= T0/2
Sb2= T16 + T0 + T0/2
Sc1= T0/2
Sc2= T0 + T21 + T0/2
97
Hexagono grande:
Sector 1:
Se aprecia en la figura A-13 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T22 + T23 + T0/2
Sa2= T22 + T0 + T23 + T0/2
Sb1= T23+T0/2
Sb2= T0 + T23 + T0/2
Sc1= T0/2
Sc2= T0+T0/2
Sector 2:
Se aprecia en la figura A-14 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T23+ T0/2
Sa2= T0 + T23+ T0/2
Sb1= T24+T23+T0/2
Sb2= T24 + T0 + T23+T0/2
Sc1= T0/2
Sc2= T0+T0/2
98
Sector 3:
Se aprecia en la figura A-15 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T16 + T21 + T0/2
Sa2= T16 + T0 + T21 + T0/2
Sb1= T0/2
Sb2= T16 + T0 + T0/2
Sc1= T0/2
Sc2= T0 + T21 + T0/2
Sector 4:
Se aprecia en la figura A-16 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T0/2
Sa2= T0+T0/2
Sb1= T0/2+T25
Sb2= T25 + T0 + T0/2
Sc1= T26+T25+T0/2
Sc2= T26+T0+T25+T0/2
99
Sector 5:
Se aprecia en la figura A-17 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T27+T0/2
Sa2= T0 + T27 + T0/2
Sb1= T0/2
Sb2=T0 + T0/2
Sc1= T26+T27+T0/2
Sc2= T26+T0+T27+T0/2
Sector 6:
Se aprecia en la figura A-18 la distribución de los tiempos de conmutación.
De esta manera los tiempos de conmutación para cada interruptor quedan
expresados de la siguiente forma.
Sa1= T22 + T27 + T0/2
Sa2= T22 + T0 + T27 + T0/2
Sb1= T0/2
Sb2= T0 + T0/2
Sc1= T0/2+T27
Sc2= T0 + T27 + T0/2
100
Figura A-1
Figura A-2
Figura A-3
101
Figura A-4
Figura A-5
Figura A-6
102
Figura A-7
Figura A-8
103
Figura A-9
v1
v20
v3
v19
v2
v19
sa1
sa2
sb1
sb2
sc1
sc2
Figura A-10
v3
v20
v1
104
Figura A-11
Figura A-12
Figura A-13
105
v1
v24
v3
v23
v2
v23
sa1
sa2
sb1
sb2
sc1
sc2
Figura A-14
Figura A-15
v3
v24
v1
106
v1
v26
v3
v25
v2
v25
sa1
sa2
sb1
sb2
sc1
sc2
Figura A-16
Figura A-17
v3
v26
v1
107
Figura A-18