Un modelo matemático para el diseño de quimioterapias con el uso

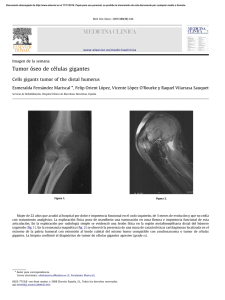
FARAUTE, Vol. 6, No. 1, 27-38, 2011
ISNN 1698-7418
Deposito Legal PP200402CA1617
Un modelo matematico para el diseño de quimioterapias con el uso de
drogas citotoxicas y citoestaticas
Soraya Aguilar1 *, Minaya Villasana 2
1
Universidad José Antonio Páez. Facultad de Ingenierı́a. Escuela de Ingenierı́a en Computación
Simón Bolı́var . Departamento de Cómputo Cientı́fico y Estadı́stica
*Autor de correspondencia: [email protected]
2 Universidad
Resumen
Se plantea una modificación a un modelo matemático previo, que simula la interacción entre
las células cancerosas y las del sistema inmune con una droga citotóxica, que actúa en
una fase especifica del ciclo celular. Aquı́ agregamos al modelo una droga citoestática, cuyo
efecto es retener las células en una fase del ciclo, con el objetivo de maximizar la cantidad
de células en una fase vulnerable para la droga citotóxica. El problema se plantea como uno
de optimización, que se resuelve usando estrategias evolutivas, se plantea y se comparan
ocho funciones objetivo. La mejor función objetivo se compara con un protocolo derivado
de un problema similar que no incluye la nueva droga. Se confirma que la combinación con
la nueva droga, mejora la efectividad de la droga citotóxica. Se argumenta, que el enfoque
propuesto puede servir como una herramienta de apoyo al médico para diseñar un esquema
tratamientos de quimioterapias.
Palabras Claves: Citotóxica, Citoestática, Ecuaciones diferenciales con retardo, Ciclo celular,
Control óptimo
Abstract
A modification of a previous mathematical model that simulates the interaction between
cancerous cells and immune system cells and a cytotoxic drug, which acts upon a specific
phase of the cell cycle is presented. Here we modify the model by incorporating a cytostatic
drug, which arrests cells in a specific phase of its cycle. The rationale behind this is to maximize
the amount of cells in the most vulnerable phase of their cycle with respect to the action of the
cytotoxic drug. The problem is posed as an optimal control problem and is solved using an
evolutionary strategy algorithm. Various objective functions are studied and compared against
previously obtained chemotherapy schedules that only incorporated the cytotoxic drug. Results
confirm that the inclusion of the cytostatic drug increases the cytotoxic’s effectivity. We argue
that this approach may serve as a valuable tool for the medical community when designing
chemotherapy treatments.
Keywords: Cytotoxic, Cytostatic, Delay differential equations, Cell Cycle, Optimal Control
28
Un modelo matemático para el diseño de quimioterapias
Introducción
Cuando se diseñan esquemas de aplicación de tratamientos de quimioterapia a los pacientes de cáncer,
el objetivo es eliminar las células cancerosas, afectando lo menos posible la salud del paciente. Se debe
tomar en cuenta que las drogas citotóxicas usadas en
estos tratamientos actúan no solo sobre las células
cancerosas sino también sobre las células del sistema inmune y células normales, afectando la salud
del paciente. Se han planteado diversos modelos matemáticos que simulen el comportamiento de las células ante distintas situaciones; como es el caso de la
reacción de las células ante variedades de esquemas
de aplicación de drogas antineoplásticas, y cómo estas afectan la salud del paciente. En (Villasana &
Radunskaya, 2003) se plantea un modelo de ecuaciones diferenciales con retardo para la dinámica de
las células cancerosas y del sistema inmune. El modelo contempla el efecto de una droga citotóxica en
fases especı́ficas del ciclo celular y sobre el sistema
inmune del paciente. De los resultados obtenidos en
(Villasana, 2001), se desprende que la sincronización
de las fases celulares podrı́a mejorar el desempeño
de la droga citotóxica. Esta sincronización se podrı́a
lograr con la inclusión de una droga citoestática en el
modelo.
La función principal de una droga cito-estática es
atrapar las células en una fase particular del ciclo celular. Al disminuir los niveles de la droga citoestática,
las células son liberadas para continuar su ciclo de
celular. Este tipo de droga se utiliza para lograr una
sincronización de células en el ciclo. La idea detrás
de la sincronización es aumentar la cantidad de células que se encuentran en la fase de mitosis y en ese
momento aplicar la droga cito-tóxica, maximizando
el efecto de esta droga sobre el tumor. La suposición
anterior se basa en los resultados obtenidos en (Villasana, 2001), donde se observó de forma empı́rica
que la sincronización de las células en el ciclo celular
aumentaba el volumen de la región de atracción del
punto de equilibrio.
Por otra parte, en la actualidad los métodos de
optimización heurı́sticos se han usado para resolver
problemas para los cuales no existe un método que
lo resuelva en un tiempo razonable. Tal es el caso del
problema de la búsqueda de protocolos de quimioterapias, que se puede plantear como un problema
de control óptimo, en donde la idea es encontrar un
Soraya Aguilar y Minaya Villasana
esquema que maximice el efecto de las drogas sobre
las células cancerosas, pero afectando lo menos posible la salud del paciente. En (Villasana & Ochoa,
2004), se plantea un problema de control óptimo
para diseñar esquemas de aplicación de quimioterapias para una única droga cito-tóxica, y se comparan
3 métodos de optimización heurı́sticos (algoritmos
genéticos, estrategias evolutivas y recocido simulado)
para resolverlo; usando como base el modelo planteado en (Villasana & Radunskaya, 2003). La droga
cito-tóxica que se considera en (Villasana & Radunskaya, 2003), ejerce su efecto sobre la fase de mitosis
de la célula. Además, esta droga no sólo afecta las
células cancerosas sino también las células del sistema inmune, las cuales son de vital importancia en la
salud del paciente, por lo que se debe tomar en cuenta
a la hora de diseñar un esquema de aplicación de tratamiento. Otros trabajos abordan el problema desde
distintos puntos de vista. En (Tse et al, 2007) los autores presentan un modelo para simular la respuesta
de las células cancerosas bajo el efecto de múltiples
drogas. Su modelo toma en cuenta tres drogas en el
tratamiento de quimioterapia, y considera la resistencia de las células a determinada droga, modelando
la cantidad de células totales presentes que son resistentes a cada una de las drogas y a la combinación
de ellas. Sin embargo, no hace una separación de las
distintas fases celulares ni de la acción de las drogas
sobre dichas fases. También se plantea un problema
de control óptimo cuyo objetivo es minimizar el tamaño del tumor bajo un conjunto de restricciones,
determinando que el controlador es de tipo “bang
- bang” (soluciones que sólo pueden tomar valores
máximos y mı́nimos) y usan un algoritmo memético
para resolverlo.
En (Liang & Leung, 2006) se plantea un modelo
de ecuaciones diferenciales que toma en cuenta la
cantidad de células malignas presentes, la concentración de la droga en el organismo y la toxicidad
acumulada de la droga en el organismo. Allı́ también
se plantea un problema de optimización con un control de tipo bang -bang, utilizando una técnica basada
en algoritmos genéticos adaptativos con elitismo para
resolverlo.
En (Swierniak et al, 1996) los autores plantean
un sistema de ecuaciones diferenciales para modelar la población de células cancerosas proliferativas
bajo el efecto de drogas cito-tóxicas y cito-estáticas,
basándose en el diseño de esquemas de aplicación de
FARAUTE Ciens. y Tec., 6(1)2011
29
Un modelo matemático para el diseño de quimioterapias
quimioterapias periódicos. Por otra parte plantean el
problema de optimización en dos enfoques, uno es la
minimización de la cantidad total de células malignas
y a su vez la minimización de la acción de la droga en
las células normales; el otro enfoque es la maximización de la cantidad de células normales y a su vez la
maximización de la acción de la droga sobre las células malignas. El modelo planteado por (Swierniak et
al, 1996) toma en cuenta las distintas fases celulares
ası́ como también la acción de la droga sobre una fase
celular especı́fica. Los autores resuelven el problema
de control óptimo de forma analı́tica para el caso de
una sola aplicación de la droga, obteniendo como
solución óptima una en la que no se presenta un solapamiento en la aplicación de ambas drogas. En otras
palabras, primero se aplica una droga (cito-estática)
para luego aplicar la otra (cito-tóxica). Este resultado sugiere una sincronización previa con la droga
cito-estática para luego aplicar una droga cito-tóxica.
Sin embargo, los modelos utilizados son simples y
no especifican la acción sobre las distintas etapas del
ciclo celular como tampoco contemplan aplicaciones
sucesivas de las drogas.
En este estudio, se tomó el modelo planteado en
(Villasana & Radunskaya, 2003) como base y se consideró una versión modificada para incluir una droga
de tipo cito-estática. Para este nuevo modelo se plantearon distintas opciones para el problema de control
óptimo, siempre teniendo como meta minimizar el
número de células cancerosas y mantener el número
de células del sistema inmune por encima de un nivel
mı́nimo aceptable. El problema de control óptimo
se formula empleando distintas funciones objetivo,
con la finalidad de encontrar cuál es la que genera
esquemas de quimioterapias más eficientes para el
paciente. El planteamiento del problema en este trabajo, está basado en el estudio de (Villasana & Ochoa,
2004), modificando la representación de la solución
para incluir la nueva droga.
El artı́culo tiene la siguiente estructura: en la sección 2 se describen las bases biomédicas que soportan
la investigación, que incluye el modelo matemático
previo, en la sección 3 se presenta el modelo matemático modificado donde se incluye la dinámica
para la droga citoestática y se describe el problema de
optimización planteado. En la sección 4 se muestran
los resultados y discusiones y finalmente la sección 5
presenta las conclusiones y las ideas que este trabajo
aportó para otras investigaciones.
Soraya Aguilar y Minaya Villasana
Formulación del problema
Bases Biomédicas
El ciclo celular es el proceso mediante el cual una
célula crece y se divide en dos células hijas. Todas las
células se originan únicamente por la división de otra
célula ya existente. Una célula puede encontrarse en
dos fases en el ciclo celular, claramente diferenciadas:
La fase de no división o interfase. Consta de
3 etapas: G1 es una etapa de descanso o fase
pre-sintética, S es la segunda etapa del ciclo,
también conocida como periodo sintético y G2
es otra etapa de descanso, también llamada
etapa post-sintética
La fase de división o mitosis.
En ocasiones, una célula que se dice cancerosa,
escapa a los controles normales de división y muerte
celular y pierde la habilidad de autoregulación. En
estos casos, se presenta el crecimiento descontrolado
y diseminación de células anormales en el organismo,
que invaden y dañan tejidos y órganos.
La mayorı́a de las drogas usadas en los tratamientos de quimioterapias afectan las células en una
fase del ciclo celular, tal es el caso de las drogas de
tipo citotóxicas que atacan las células en alguna fase especı́fica y las drogas de tipo citoestáticas cuya
función es atrapar las células en interfase. Con altas
concentraciones de la droga cito-estática se provoca una sincronización en el ciclo celular puesto que,
cuando la concentración disminuye las células son
liberadas y continúan el ciclo.
Modelo Matemático
En el modelo matemático usado en (Villasana &
Radunskaya, 2003) se considera la población de células del tumor durante la interfase en el tiempo, TI (t),
la población de células del tumor en la fase de mitosis,
TM (t), la población de células del sistema inmune,
I(t), la cantidad de droga presente a tiempo t, u(t) y
el tiempo de duración de las células en interfase, τ.
Aquı́ se considera las células citotóxicas T en representación del sistema inmune por su importancia en
el combate del cáncer. El modelo puede describirse
mediante el siguiente sistema de ecuaciones:
FARAUTE Ciens. y Tec., 6(1)2011
30
Un modelo matemático para el diseño de quimioterapias
dT1
dt
dTM
dt
dI
dt
du1
dt
du2
dt
u(t)
=
2a4 TM − (c1 I + d2 )T1 − a1 T1 (t − τ)
=
a1 T1 (t − τ) − d3 TM − a4 TM − c3 TM I − k1 (1 − e−k2 u )TM
=
k+
=
−λ1 u1 + c(t)
=
−λ2 u2 + c(t)
=
r1 u1 (t) + r2 u2 (t)
ρI(T1 + TM )n
− c2 IT1 − c4 TM I − k3 (1 − ek4 u )I
α + (T1 + TM )n
(1)
=
=
=
=
=
φ1 (t)
φ2 (t)
φ3 (t)
0
0
exponenciales separadas, donde cada una representa
una tasa de eliminación distinta. Una representa una
tasa de decaimiento rápida que se da mientras la droga se distribuye a través de la sangre a los tejidos, y
la otra es una tasa de decaimiento más lenta de los
tejidos periféricos. Esta función de decaimiento se
expresa como
decay(t) = r1 e−λ1t + r2 e−λ2t
Con los datos iniciales dados por:
TI (t)
TM (t)
I(t)
u1 (0)
u2 (0)
Soraya Aguilar y Minaya Villasana
para
para
para
t ∈ [−τ, 0]
t ∈ [−τ, 0]
t ∈ [−τ, 0]
Donde:
d2 TI , d3 TM y d1 I. representan la proporción natural de muerte celular
a1 y a4 son las tasas de reproducción del tumor
ci representan las pérdidas de los encuentros de
las células tumorales con las células inmunes.
ρI(TI +TM )n
α+(Ti +TM )n ,
representa el crecimiento no lineal
de la población de células del sistema inmune
debido a la presencia de células cancerosas.
ρ y a representan la habilidad del organismo
de producir ciertas citotoxinas y dependen del
tipo de tumor a ser considerado y del sistema
inmune
k, representa la tasa constante de producción
de células del sistema inmune
τ, es el tiempo que reside la célula en la etapa
de interfase
TM I y TI I representan las pérdidas debidas a los
encuentros entre los diferentes tipos de células
−k1 (1 − e−k2 u )TM , representa las células del
tumor que no proliferan al ser sacadas fuera
del ciclo celular por la acción de la droga
La droga citotóxica que se estudia en (Villasana
& Radunskaya, 2003) es Paclitaxel, la cual tiene un
decaimiento que puede ser modelado por dos curvas
(2)
donde r1 y r2 son constantes adimensionales.
Sean u1 y u2 tales que, la concentración de la
droga en cualquier tiempo está dada por una combinación lineal u(t) = r1 u1 (t) + r2 u2 (t).
Las dos últimas ecuaciones del sistema de ecuaciones diferenciales (1) modelan la situación con
múltiples aplicaciones de droga citotóxica durante
el tiempo, y son identificadas con la función c(t), la
cual es la concentración de Paclitaxel que entra al
sistema a tiempo t.
El sistema libre de droga puede tener hasta 5
puntos de equilibrio dependiendo de los valores de
los parámetros libres del modelo.
Uno de estos puntos es (0, 0, I0 ) con I0 = k/d1 >
0, el cual siempre está presente. Este punto representa
un sistema libre de células cancerosas, con población
del sistema inmune positiva, el cual es un escenario
deseable.
Cuenca de atracción
En el punto de equilibrio (TI , TM , I) = (0, 0, I0 ),
con I0 > 0 y u = 0, no hay células cancerosas presentes en el organismo y un número positivo (I0 )
de células del sistema inmune. Este es un escenario
deseable y es el punto de equilibrio al cual se quiere
que el sistema converja. En (Villasana & Radunskaya,
2003) se estudiaron las condiciones sobre el espacio
de parámetros para garantizar la estabilidad del punto
de equilibrio libre de tumor. En este trabajo se fijaron los parámetros libres a valores que garantizan
la estabilidad del punto de equilibrio libre de tumor,
tomando en consideración el rango fisiológicamente
viable para cada parámetro, de modo que el punto es
un atractor local de trayectorias vecinas. Los valores
utilizados se resumen en la Tabla 1. La idea principal
del estudio es llevar el sistema dentro de la cuenca de
atracción de este punto.
La cuenca de atracción del punto de equilibrio se
define como el conjunto de funciones iniciales (historia) φ , para las cuales las trayectorias van hacia el
FARAUTE Ciens. y Tec., 6(1)2011
31
Un modelo matemático para el diseño de quimioterapias
Tabla 1. Valores de los Parámetros
Parámetros
τ
a1
a4
d2
d3
c1 = c3
c2 = c4
k
d1
n
ρ
α
Valores Estimados
22 hr (0.9167 dia)
0.8470 dia−1
0.9159 dia−1
0.1145 dia−1
0.6641 dia−1
2,16x10−10 célula−1 dia−1
3,422x10−10 célula−1 dia−1
1,3x104 célula−1 dia−1
0.04 dia−1
3
0.2 dia−1
(0,3x106 célula)3
punto de equilibrio. Es difı́cil determinar analı́ticamente la cuenca de atracción de un punto de equilibrio. En este caso se presenta una aproximación
numérica de la cuenca de atracción para el punto de
equilibrio libre de tumor en la Fig 1, que aparece en
(Villasana, 2001).
Soraya Aguilar y Minaya Villasana
librio libre de tumor. Se considera que el punto que
representa a una función de historia converge a un
punto de equilibrio si la distancia del punto final de la
integración (luego de 500 dı́as) al punto de equilibrio
disminuye con respecto a la distancia medida desde
la posición inicial a tiempo 0. Tales funciones objetivos se dicen pertenecientes a la cuenca de atracción
del punto libre de tumor.
Modelo matemático incluyendo la
droga citoestática en el modelo
La función de una droga cito-estática es retener la
célula en una fase del ciclo celular y en este caso, es
de interés la retención en la fase G1, una de las etapas
de la interfase. Es por esto que el término a modificar
en el modelo es a1 T1 (t − τ) en la ecuación de dTdtM
que representa la cantidad de células que entran a la
fase de mitosis provenientes de interfase. La droga
estudiada es Iressa, para la cual los fabricantes (Life
Extensión Magazine, 2000) revelan que después de 3
dı́as de tratamiento el 100 % de las células es retenida
en la fase G1.
De acuerdo a nuestros estudios preliminares, la
concentración de la droga en el organismo se satura a
333mg, considerando el suministro de 250mg diarios
y la tasa de eliminación de la droga por el organismo.
Esta concentración máxima se alcanza después de
tres dı́as de administración de la droga. Asumiendo
un efecto lineal se puede expresar el efecto de Iressa
E(v) en función de los niveles de su concentración
(v) de la siguiente forma
E(v) =
Figura 1. Región de Atracción del punto fijo (0, 0, I0 ).
Los ejes TI y TM en la Fig 1 representan el número
de células en interfase y en mitosis respectivamente,
mientras que el eje z representa el número de células
del sistema inmune. Cada punto en el espacio tridimensional representa una función inicial con valor
constante en cada componente (TI , TM , I). Los puntos
al interior de la región delimitada por la ‘cascada’ pertenecen al conjunto de funciones iniciales tales que
usadas como funciones de historia al sistema libre de
droga en (1), las órbitas convergen al punto de equi-
1
− 333
v+1
0
0 ≤ v ≤ 333
v > 333
(3)
Tomando en cuenta estos datos, se puede decir
que cuando la concentración de Iressa está en 333
mg, ninguna célula pasa de TI a TM , y cuando la
concentración de la droga está en 0 no hay ningún
efecto sobre el paso de las células entonces se puede
modificar el término en la expresión original a1 T1 (t −
1
τ) a max(0, − 333
v + 1)a1 T1 (t − τ)
También es necesario agregar al modelo la ecuación que simula la disminución de la nueva droga
en el organismo. Para esto, asumimos un modelo
exponencial para modelar el decaimiento de la concentración de Iressa y utilizando datos de vida media
FARAUTE Ciens. y Tec., 6(1)2011
32
Un modelo matemático para el diseño de quimioterapias
de la droga, se puede determinar que
p
decay v(t) = exp(ln( (2) ∗ t))
(4)
El modelo planteado en el cual se incluye la droga
cito-estática quedarı́a como:
dT1
dt
dTM
dt
dI
dt
= 2a4 TM − (c1 I + d2 )T1 − a1 T1 (t − τ)
1
v + 1)a1 T1 (t − τ) − d3 TM
333
−a4 TM − c3 TM I − k1 (1 − e−k2 u )TM
ρI(T1 + TM )n
− c2 IT1 − c4 TM I
= k+
α + (T1 + TM )n
= max(0, −
−k3 (1 − ek4 u )I
du1
dt
du2
dt
dv
dt
(5)
= −λ1 u1 + c(t)
Soraya Aguilar y Minaya Villasana
está presente en la minimización de todas las
funciones planteadas, ya que el objetivo del estudio se basa principalmente en la eliminación
de las células cancerosas.
TM (t f ) es el número de células en la fase de
mitosis al final del tratamiento. Al igual que el
caso anterior, está presente en todas las funciones planteadas, ya que las células cancerosas
se componen de la cantidad de células en TI
más la cantidad de células de TM .
1
tf
R tf
0 TI (t) + TM (t) dt. es la cantidad promedio
de células cancerosas a lo largo del tratamiento. Este factor está presente en algunas de las
funciones objetivos planteadas. La idea detrás
de este término es prevenir picos abruptos en
los niveles del tumor a lo largo del tratamiento.
PU es la cantidad de ciclos usados para la aplicación de la droga cito-tóxica. En general se
desea minimizar la cantidad de droga utilizada
lo cual podrı́a traducirse en una disminución
de los ciclos de tratamiento.
= −λ2 u2 + c(t)
p
= −ln( (2))v + cv (t)
donde cv es una nueva variable de control, que representa la concentración de la droga cito-estática que
entra al sistema en el tiempo t.
El Problema de Control Óptimo
En este estudio se plantea el problema del diseño de quimioterapias como un problema de control
óptimo, donde el objetivo principal es minimizar el
número de células cancerosas presentes en el sistema,
manteniendo el nivel de células del sistema inmune
sobre un nivel mı́nimo establecido. Dado que el tipo de solución es bang-bang, la variable a controlar
es el tiempo de aplicación y descanso de las drogas
cito-tóxicas y cito-estáticas, por lo cual cada solución
estudiada plantea un posible esquema de aplicación
y descanso de ambas drogas a lo largo del tiempo del
tratamiento.
En este trabajo se plantearon diversas funciones
objetivos, para buscar cuál es la que genera mejores
esquemas para la eliminación del tumor y sin perjudicar el sistema inmune del paciente. Se tomaron en
cuenta distintos factores para cada función objetivo,
los cuales se describen a continuación
TI (t f ) es el número de células en interfase al
final del tratamiento. Este es un factor que
SDU es la suma de los tiempos de descanso en
el esquema de la droga cito-tóxica. Se incluye
la maximización de este término en algunas
funciones para dar más tiempo al paciente de
recuperarse entre aplicaciones de U.
I − γImax ≥ 0, con I la cantidad de células del
sistema inmune, y γImax el valor mı́nimo establecido para la cantidad de células del sistema inmune. Esta restricción controla que a
lo largo del tratamiento la diferencia sea positiva para asegurar que el número de células
no descienda por debajo de este mı́nimo. Si en
algún momento se viola esta restricción se le
impone una penalización a la función objetivo.
Tomando en cuenta lo anterior se incluye en las
funciones el término ζ (I − γImax ), donde ζ es
la constante de penalización que se le impone
cuando se viola la restricción del sistema inmune. Dada la importancia de este término, este
fue incluido en todas las funciones estudiadas.
Los términos:| TI (t f ) − 0,3 | y , | TM (t f ) − 0,3 |
se incorporan con el fin de llevar el sistema al
punto (0,3, 0,3, I0 ) que es un punto conocido
dentro de la cuenca de atracción del punto fijo
FARAUTE Ciens. y Tec., 6(1)2011
33
Un modelo matemático para el diseño de quimioterapias
estable (0, 0, I0 ). Por ser este punto un atractor, si el sistema llega a un punto dentro de la
cuenca se considera al paciente como curado.
Las funciones objetivo analizadas son:
F1 : TI (tt f ) + TM (t f ) + t1
f
F2 : TI (tt f ) + TM (t f ) +
R tf
0
TI (t) + TM (t) dt + ζ (I − γImax )
1 R tf
t f 0 TI (t)
+ TM (t) dt + PU + ζ (I −
γImax )
F3 : TI (tt f ) + TM (t f ) + PU + ζ (I − γImax )
F4 : | TI (t f ) − 0,3 | + | TM (t f ) − 0,3 | + t1
f
R tf
0
TI (t) + TM (t) dt +
PU + ζ (I − γImax )
F5 : | TI (t f ) − 0,3 | + | TM (t f ) − 0,3 | +PU + ζ (I − γImax )
F6 : | TI (t f )−0,3 | + | TM (t f )−0,3 | +PU −SDU +ζ (I −γImax )
F7 : | TI (t f ) − 0,3 | + | TM (t f ) − 0,3 | −SDU + ζ (I − γImax )
F8 : | TI (t f ) − 0,3 | + | TM (t f ) − 0,3 | + t1
f
R tf
0
TI (t) + TM (t) dt −
SDU + ζ (I − γImax )
El método utilizado para resolver el problema de
optimización asociado fue la Estrategia Evolutiva con
matriz de covarianza adaptativa, que fue el que obtuvo mejores resultados en (Villasana & Ochoa, 2004).
Los experimentos fueron realizados en la plataforma
Matlab (Mathworks) y utilizamos una versión libre
del método provista por el autor para esta plataforma.
(Hansen, 1996).
Para calcular los valor de TI , TM e I en (1), se resuelve el sistema de ecuaciones diferenciales con retardo usando la rutina dde23, el cual es la implementación propietaria del método publicado en (Shampine & Thompson, 2001), y que está incluida en la
colección de métodos de Matlab.
Los valores por defecto de los parámetros del
paquete son: El número de hijos 3bb se calcula como λ = 4 + b3lnNc, donde N es la longitud de una
solución, y el número de padres µ se calcula como
µ = bλ /2c. Para este estudio N = 62 por lo tanto
λ = 16 y µ = 8, y la población se calcula con la
estrategia (µ, λ ) por lo que queda una población de
24 individuos. Los experimentos se hicieron con 100
iteraciones para alcanzar las 1600 evaluaciones de
la función objetivo, la cual se determinó experimentalmente como suficientes iteraciones para la convergencia del método.
Soraya Aguilar y Minaya Villasana
En este trabajo la representación seleccionada
para cada posible solución son duplas en la que la primera componente representa el tiempo de aplicación
de una droga y la segunda componente representa el
tiempo de descanso de la misma droga, cada dupla
representa un ciclo dentro del esquema de aplicación.
Se tomaron 15 ciclos como máximo para cada
droga dentro de un protocolo. Este valor se estableció como un valor lo suficientemente grande como
para obtener un protocolo de quimioterapia eficaz,
tomando en cuenta que en (Villasana & Ochoa, 2004)
se usaron 9 ciclos de aplicación.
La estructura usada para almacenar una posible
solución es un vector de 62 posiciones, en el cual
las primeras 30 posiciones representan las 15 duplas
del esquema de aplicación de la droga citotóxica (denominada U en este estudio), las 15 posteriores son
las duplas del esquema de aplicación de la droga
cito-estática (denominada V en este estudio), las dos
últimas posiciones representan el número de ciclos de
U (droga cito – tóxica) y de V (droga cito – estática)
(denominadas PU y PV en este estudio), estos valores
son calculados por el algoritmo.
Resultados y discusión
Para medir los resultados se tomaron algunos indicadores que ayuden a medir la eficiencia y eficacia
de la solución, evaluando distintos aspectos. Estos
indicadores son:
1. Interfase: Área bajo la curva para las células
cancerosas en interfase y mitosis.
2. ISH: Immune System Health (Salud del Sistema Inmune). Mide el área bajo la curva de
I − 0,9 que es el valor mı́nimo establecido para
la cantidad de células del sistema inmune.
3. TD: Target Desviation. Mide la desviación del
sistema a los valores objetivos al final del tratamiento. Para algunas funciones objetivo el valor objetivo final de la dupla (TI , TM ) es (0, 0);
y para otras funciones es (0,3, 0,3).
4. SOLAP: Se mide el tiempo de aplicación en el
cual se aplican ambas drogas U y V simultáneamente.
5. PU: Número de ciclos del esquema para U.
FARAUTE Ciens. y Tec., 6(1)2011
34
Un modelo matemático para el diseño de quimioterapias
La Tabla 2 muestra los resultados obtenidos para
cada función objetivo planteada, mostrando los valores promedios los mejores valores obtenidos de 10
corridas por cada función.
6. También se observa que para el tiempo total de
tratamiento, el tiempo de solapamiento es bastante corto, apenas alcanza en promedio para
todas las funciones el 1.5 % del tiempo total de
tratamiento. Lo que se puede concluir es que
el algoritmo favorece el no solapamiento de
ambas drogas, lo que va en concordancia con
investigaciones de trabajos anteriores (Swierniak et al, 1996).
Tabla 2. Resultados de mejor valor obtenido de 10
corridas para las funciones objetivo planteadas
F.O.
F1
F3
F4
F5
F6
F7
F8
Interfase
285,591
368,014
349,362
343,795
657,731
629,737
661,621
ISH
13,857
13,669
18,09
8,1412
25,763
25,732
25,73
TD
0,213
0,214
0,013
0,009
0,01
0,01
0,011
SOLAP
4,9242
11,3658
1,2039
4,8799
0,1999
0,1999
5,0755
PU
15
15
15
10
15
15
15
Algunas observaciones que se derivan de la tabla
son:
1. La función objetivo en la cual se elimina la
mayor cantidad de células del tumor es la correspondiente a la ecuación F1 .
2. la función objetivo que tiene mejores resultados con respecto al sistema inmune es la correspondiente a la ecuación F8 . En general se
puede decir que las funciones que incluyen el
punto (0,3, 0,3, I0 ) tienen mejores resultados
con respecto a la salud del paciente.
Soraya Aguilar y Minaya Villasana
Dados los resultados de la Tabla 2, se puede decir
que se ve una clara diferencia entre los resultados
que incluyen el término SDU en la función objetivo
y los que no en cuanto a que se tiene mayor cantidad
de células cancerosas pero esto es producto de que al
tener mayor tiempo de descanso entre las aplicaciones de la droga citotóxica se obtienen tratamientos
más largos en el tiempo. Sin embargo estos son tratamientos que afectan menos la salud del paciente
que es un escenario ideal. También se puede observar
que se acerca al punto deseado al final del tratamiento, lo que se puede interpretar como un tratamiento
efectivo.
En la Fig 2 se puede observar un esquema de
aplicación de quimioterapia obtenida con la función
objetivo que no incluye la integral, y en la Fig 3 un
esquema de aplicación de quimioterapias que incluye la integral. Se puede observar la diferencia en la
aplicación de la droga cito-tóxica entre ambas funciones. De este estudio se desprende de forma empı́rica
3. La que más se acercó al punto objetivo son
las correspondientes a la ecuaciones F6 y F7
(menor valor para TD), pero con resultados
bastante duros para el sistema inmune. Dado
que la mejorı́a en TD no fue significativa con
respecto a las demás funciones, estas no parecieran balancear apropiadamente los diversos
objetivos.
4. El término PU no pareciera ser relevante en la
minimización.
Figura 2. Esquema de tratamiento obtenido con la
5. La inclusión del término SDU en la función
objetivo ofrece excelentes resultados sobre el
sistema inmune, pero empeora el nivel de tumor durante el tratamiento. Sin embargo, el
nivel de tumor al final del tratamiento es comparable con otras funciones.
que la inclusión de la integral en la función objetivo
obtiene esquemas que maximizan los tiempos de descanso y minimizan los tiempos de aplicación de la
droga cito-tóxica al final del tratamiento, lo cual es
un escenario ideal para el paciente.
Comparación con resultados previos
F7
FARAUTE Ciens. y Tec., 6(1)2011
35
Un modelo matemático para el diseño de quimioterapias
Soraya Aguilar y Minaya Villasana
que el tratamiento que incluye solo a U que sólo lleva
el valor de TD a 0,4769 en el mismo tiempo.
Conclusiones y Otros trabajos
Figura 3. Esquema de tratamiento obtenido con la
F8
Se consideraron algunas medidas para comparar
los resultados actuales con los resultados en trabajos
anteriores (Villasana & Ochoa, 2004), donde sólo se
utilizaban drogas cito-tóxicas en el protocolo de quimioterapia. Solamente se realizó la comparación con
la primera función objetivo ya que es la única que
se repite en ambos trabajos. Dado que el tratamiento
que incluye las drogas U y V es más largo en el tiempo y para hacer una justa comparación, se truncó la
solución en función del tiempo del tratamiento que
solo usa la droga U. Se consideró además en ambas
funciones objetivos que el sistema debe aproximarse
al punto fijo (0, 0, I0 ), obteniendo los resultados de la
Tabla 3.
Tabla 3. Comparación de esquemas hallados por la
Estrategia Evolutiva incluyendo la droga citoestática y sin
incluirla.
Incluyendo U y V
Sin Incluir V
Interfase
13,857
13,669
ISH
0,213
0,214
TD
4,9242
11,3658
PU
15
15
En la Tabla 3, se puede observar la disminución
de los valores de las células cancerosas, por lo que
se puede decir que el tratamiento que incluye ambas drogas es más efectivo tomando en cuenta que
tiene patrones de administración similares. Esto indica que la inclusión de la droga cito-tóxica aumenta
la efectividad del tratamiento. También se observa
una disminución en el número de células al final del
tratamiento, y estas mejoras se obtienen sin mayor
perjuicio a la salud del sistema inmune. También hay
que tomar en cuenta que el tratamiento que incluye
ambas drogas llega al valor de TD 0,2058 al final del
tratamiento completo, lo que es mucho más efectivo
Se observa una mejorı́a con respecto a los valores
del tumor a lo largo y al final del tratamiento cuando
se incluyen ambas drogas, por lo que se puede concluir que la inclusión de una droga cito-estática puede
mejorar la efectividad de la droga cito-tóxica, sin que
el sistema inmune se vea perjudicado. Por otra parte,
el algoritmo encuentra tratamientos más largos que
en el trabajo anterior (Villasana & Ochoa, 2004), lo
que pudiese ser más molesto para el paciente, pero
el valor del TD (Target Desviation) después de terminar el tratamiento completo presenta una mejora
significativa con respecto a los resultados anteriores.
La mejor función objetivo encontrada en nuestro
estudio comparativo preliminar fue
| TI (t f ) − 0,3 | + | TM (t f ) − 0,3 | + t1f
TM (t) dt − SDU + ζ (I − γImax )
R tf
0
TI (t) +
ya que consigue buenos resultados en cuanto
a la eliminación del tumor a lo largo del tratamiento,
y al final del mismo reporta una reducción tan
buena como otras funciones en las cuales éste es
el objetivo principal y único. Esta función objetivo
arroja soluciones que representan un patrón ideal
para el paciente, en el que al final del tratamiento
se aplica muy poca droga U, lo que permite una
recuperación del mismo. Este hecho se evidencia en
los valores del sistema inmune en los que se ve una
mejora significativa (dinámica no mostrada).
Se pudo observar después de varios experimentos que el efecto que tiene el término de la integral
sobre el esquema es la regularidad en los tiempos de
descanso de U, que es un aspecto deseable dentro
de la solución desde el punto de vista de la calidad
de vida del paciente. La inclusión de PU no tiene
ninguna influencia ya que el problema no minimiza
esta cantidad y las soluciones tienden a considerar el
máximo número de ciclos. La suma de los tiempos
de descanso de U tiene un efecto positivo en la salud
del sistema inmune aunque desmejora la cantidad de
células cancerosas a lo largo del tratamiento. Sin embargo se puede observar que al final del tratamiento
se logra el objetivo de llevar la dinámica del tumor
dentro de la cuenca de atracción. La inclusión dentro
FARAUTE Ciens. y Tec., 6(1)2011
36
Un modelo matemático para el diseño de quimioterapias
de la función objetivo de minimizar hasta llegar a
algún punto dentro de la cuenca de atracción (como
por ejemplo al punto (0,3, 0,3, I0 )) hace que el sistema llegue muy cerca de estos valores al final del
tratamiento, considerando al paciente curado.
En las simulaciones realizadas se pudo ver que las
mejores soluciones favorecen el no solapamiento en
la aplicación de ambas drogas llegando a no superar
el 1.5 % por ciento del tiempo total de aplicación,
lo que va en concordancia con trabajos anteriores
(Swierniak et al, 1996).
Este trabajo sirvió como base para otros trabajos
(Villasana et. al, 2010) donde se hacen entonaciones al modelo matemático en la identificación del
sub-sistema de la droga cito-estática y se consideran
aquellas funciones objetivos que produjeron resultados interesantes en este estudio preliminar del sistema F4 , F5 y F6 . Otro aspecto interesante explorado
en profundidad es el efecto del solapamiento de la
aplicación de ambas drogas en el tratamiento que se
aborda considerando representaciones que permitan
el solapamiento de ambas drogas y representaciones
donde dicho solapamiento no esté permitido.
Soraya Aguilar y Minaya Villasana
Villasana M., (2001). A Delay Differential Equation
Model for Tumor Growth. Dissertation for the degree
of Doctor of Philosophy. Graduate Faculty of Mathematics. Claremont Graduate University. Claremont,
California. USA
Villasana M., Ochoa G. (2004). Heuristic Design of
Cancer Chemotherapies. IEEE Transactions on Evolutionary Computation. 8(6): 513-521.
Villasana M., Ochoa G., Aguilar S. (2010). Modeling
and Optimization of Combined Cytostatic and Cytotoxic Cancer Chemotherapy. Artificial Intelligence in
Medicine. 50(3): 163-173.
Villasana M, Radunskaya A. (2003). A delay differential equation model for tumor growth. Journal of
Mathematical Biology. 47: 270-294.
Bibliografı́a
Hansen N. (1996). The CMA evolution strategy.
http://www.lri.frhansen/cmaesintro.html
Liang Y, Leung K. (2006). A Novel Evolutionary
Drug Scheduling Model in Cancer Chemotherapy.
IEEE Transactions on information technology in biomedicine. 10: 237-245.
Life Extensión Magazine. (2000). Suppressing cancer cell growth - a novel approach.
www.lef.org/magazine/mag2000/dec2000 awsi2.html.
Consultado en Mayo de 2007.
Shampine L., Thompson S. (2001). Solving DDEs
in MATLAB. Applied Numerical Mathematics. 37:
441-458
Swierniak A., Polanski A., Kimmel M. (1996). Optimal control problem arising in cell-cycle- specific
cancer chemotherapy. Cell Proliferation. 29: 117139.
Tse L, Liang Y, Leung K. (2007). A Memetic Algorithm for Multiple Drugs Cancer Chemotherapy
Shedule Optimization. IEEE Transactions on System,
Man and Cybernetics part B. 37: 84-91.
FARAUTE Ciens. y Tec., 6(1)2011
37