Clase 2.- Compuertas y Vertedores
Anuncio

Problemas de compuertas, vertedores y salto hidráulico:
Tema 1) La Compuerta:
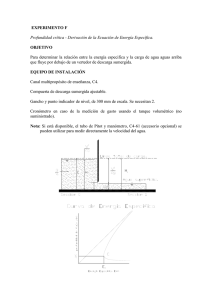
Figura 1. Alturas que intervienen en la descarga (Q) de una compuerta sumergida incluyendo el
salto hidráulico ys. Si ys = y3 la descarga es libre y el salto es claro. Si ys = y3 la descarga es
libre y el salto se corre hacia la derecha del punto 2.
La profundidad mínima del chorro a la salida de la compuerta se alcanza a una
distancia a/Cc según Sotelo, en este punto y2 se calcula como: y2 Cc a . En teoría, si
en el punto 2 se genera el salto el valor de ys tiene la máxima altura.
Teoría de la descarga Q de la compuerta: Para compuertas planas o radiales a la salida
de la corriente de agua Q se produce en un hoyo rectangular que tiene un área de
conducción A2 b y2 , bajo condiciones ideales (z1 = z2, h12 = 0) y la definición del
gasto unitario q = Q/b, la solución al problema del calculo de Q se obtiene: a) planteando una ecuación de Bernoulli de 1 a 2, b) y planteando la ecuación de Momentum
de 2 a 3. El resultado es;
y1
q2
q 2 Ecuacion de Bernoulli simplificada que resultas ser la de
y
,
a
2gy12
2gy 22 Energia Especifica y esta conduce al Numero de Froude (1)
ya2 q 2
y2 q 2
3
2 gy 2
2 gy3
,
Ecuacion de Momentum simplificada a una seccion
(2)
rectangular.
Es conveniente señalar que en el punto 2, hay dos 2 alturas; ya y y2. Por la profundidad
y2 sale el chorro de agua y entre ya y y2 se genera una zona de estancamiento.
1
Si la descarga en la compuerta es libre entonces solo se necesita la ec. de Bernoulli (1)
para resolver el problema de q = Q/b ya que para este caso: ya = y2.
La dificultad: 1) numérica para la solución del sistema de ecuaciones (1 y 2) y 2) de
medir la contracción de Cc y el coeficiente de velocidad Cv [K = 1/Cv 2 – 1] en un
laboratorio: condujeron de medir el coeficiente de descarga Cd = f(Cc,Cv,y1/a,y3/a) que
contiene todas las variables de la función f(….) el cual resulta más o menos sencillo de
medir y es más exacto y con esto el problema de calcular q es redujo a la siguiente
ecuación y graficas experimentales como la figura 6.15 y 6.16 (tomadas de Sotelo).
q Cd a 2gy1
(3)
Para un análisis más detallado sobre la compuerta y los vertedores en un libro de
texto, la referencia es; Hidráulica General, Sotelo A.G., para más detalle se debe
consultar, el texto de Henderson F.M, investigaciones del USBR, USACE, ASCE y otros.
2
El coeficiente de contracción Cc: Para el caso de compuertas planas verticales (θ = 90º)
el valor de Cc se ubica de 0.60 a 0.63 para este escrito se asume que Cc es una
constante de Cc = 0.62. Valores menores de 0.60 aparecen en la grafica de Cofré para
relaciones de profundidad y3/y1 > 0.93.
Tema 2) El salto hidráulico.
El salto se produce cuando una corriente de agua tiene un Número de Froude, Fr2 > 1 y
aguas abajo por X motivo la corriente de agua tiene un Fr2 < 1. Para que un flujo tome
un Fr2 > 1 lo más común es que esto suceda a la salida de una compuerta, al pie de un
cimacio, o al pie de una rápida (un canal con una pendiente de fondo So > Sc, donde Sc
es la pendiente critica) a la caída de un vertedor el también se puede producir un salto
pero su calculo es a través de resultados experimentales (Ver Henderson F.M, Open
Channel Flow).
El problema del cálculo del salto hidráulico se obtiene, para el caso de la compuerta
de la Figura 1 con descarga libre (y2 = ya )de plantear la ecuación de Momentum (2)
entre las secciones 2 y 3 (y3 = ys) el resultado para el cálculo de ys es:
y2
1 8Fr22 1 , Salto hidraulico de 1 a 2, si Fr22 1
(4)
2
Altura conjugada,si Fr32 1, no hay salto, (5)
y
y 2 3 1 8Fr32 1
, la formula funciona matematicamente
2
pero no hay salto.
ys y 3
Existen varias formulas obtenidas por observación, por sencillez se usara:
Ls = 6(ys – y2)
(5.1)
Una explicación más detallada del salto a nivel de libro de texto se encuentra en
Gardea H., Hidráulica de Canales o en Sotelo A.G, Hidráulica de Canales.
Aspectos prácticos: Cuando la corriente de agua sale de una compuerta por lo común
al final tendrá que descargar en un canal de tierra que es erosionable y por lo común la
velocidad en la sección 2 V2 será mayor a la velocidad permisible del canal Vp y por lo
tanto si el flujo descarga directamente en el canal de tierra este se destruye, por esto,
se debe de reducir la V2 y la forma más practica es generando artificialmente el salto,
para reducir velocidad.
Las formas de generar artificialmente el salto por lo común son:
1. Colocar aguas abajo de la compuerta un vertedor de pared delgada (como se
indica en la figura 1) o de pared gruesa.
2. Construir aguas abajo una transición vertical en el fondo del canal que se
llaman tanques de amortiguación o lagunas de disipación.
En los problemas solo se usara el vertedor de pared delgada y además por cuestiones
practicas solo se usaran en los ejemplos profundidades en el deposito y1 de 1 a 3.0m y
en compuertas comerciales con ancho b de, 1 pie, 2 y 3 pies, con el objetivo de señalar
3
que no se necesitan grandes cargas de altura y1 para generar Números de Froude, Fr2
> 1.
Tema 4) El vertedor o vertedero.
Figura 2. Una pared que represa la corriente de agua y altera la altura en el canal aguas
arriba se llama vertedor. Eliminando las contracciones horizontales la figura muestra
las condiciones más generales de operación de la pared: estas son:
1.
2.
3.
4.
Si el espesor e del vertedor es pequeño se denomina de pared delgada.
Si el espesor e del vertedor es grande se denomina de pared gruesa.
Si h’ < 0 se llama con descarga libre.
Si h’ > 0 se llama con descarga sumergida.
Para un vertedor con e pequeña y con h’ < 0 y considerando que la velocidad aguas
arriba es V1 = 0, la ecuación de Bernoulli, en forma teórica, indica que la velocidad de la
corriente agua es: v 2g(h0 h) , o sea, que en el punto 2 la velocidad es cero (v2 =
0) y en el 3 es, v3 2gh0 , o sea, es la máxima.
Para calcular el flujo de agua Q entre los puntos 1 y 2 que tienen una velocidad
variable v se recurre al calculo diferencial al expresar a Q como: dQ = v·dA y al integrar
se obtiene la respuesta.
Si la forma del vertedor es un trapecio (vertedor Cipolleti) el diferencial de área dA se
expresa como: dA/1 = T·dy = (b + 2·m·y)dy, donde, T = es el ancho de la superficie, b =
es el ancho del fondo y m = pendiente del talud.
Cambiando a y por h, esto es h = y, el cálculo de Q a través de la integral resulta:
/1
Esta formula de dA = T·dy es ampliamente usada en los libros de texto de hidráulica en el
capitulo de Energía Especifica para generalizar la formula del Número de Froude.
4
Multiplicando por (2g)1/2 el resultado obtenido de la integración para un vertedor
trapecial obtiene además la formula para los vertedores rectangulares y triangulares
como se indica en las siguientes 2 formulas.
2
2
Q 2g·bh 3/2 μ 2gh b·h μ VA·μ
3
3
sección rectangular del trapecio
8
8
Q
2gm·h 5/2 μ
2gh mh 2 μ VA·μ sección triangular del trapecio
15
15
La raíz de 2gh es la velocidad máxima en la cresta del vertedor y al multiplicar por los
coeficientes 2/3 u 8/15 se obtiene la velocidad promedio, [b·h] y [m·h 2] son el área del
rectángulo y de los triángulos.
El coeficiente μ: Los resultados entre {..} arrojan el valor teórico de Q al no incluir los
efectos de la contracción vertical de la altura h en la cresta del vertedor y de la
contracción horizontal, por esto, las formulas se deben de multiplicar por un
coeficiente experimental μ o Cd.
Vertedor triangular: uno de los usos del vertedor es medir el gasto Q y el vertedor
triangular es muy exacto, en particular de m = 1 o de 90º. Si el vertedor se usa para
medir Q la descarga debe ser libre (h’ < 0) y además, de pared delgada. Una buena
cantidad de valores de μ se encuentran en Hidráulica General capitulo 7 de Sotelo A.G.
Vertedor rectangular: este es el más usual y también se usa para elevar la carga de
altura y1 aguas arriba de la estructura. El vertedor puede ser de pared gruesa
(fabricado con mampostería) que es muy común y puede operar con descarga
sumergida(h’ > 0).
Lo anterior conlleva a tener otra formula para los de pared gruesa y diversos
coeficientes, sin embargo, Sotelo A.G propone una solución basada en 2 coeficientes
adicionales a μ y en una formula muy compacta:
Q
q 2.952·h3/2 μ·ε1ε 2
b
formula en metros
(6)
Donde q = Q/b, 2.952 = 2/3·19.621/2 y:
1. ε1 = es el coeficiente al considerar que el vertedor de pared gruesa.
2. ε2 = es el coeficiente al considerar el efecto de sumersión h’ en la descarga.
La formula propuesta para μ proviene de los datos de Rehbock y según Henderson F.M
se puede reducir a:
h
Cd μ 0.611 0.08
(7)
w
5
1
0.185
ε1 0.70
e/h
0.1
0.75
e/h
e/h 0.67 ec. de Bazin
0.67 < e/h 3
3 < e/h 10
(8)
ec. de Bazin
ec. de Gibson
Figura 3. ε2 = coeficiente de sumersión según Domínguez.
x ln 1 h'/h , Ajuste de los datos de Domninguez
1
ε2
1 h'/h > 1.2
2
3
exp 0.0216 0.1138x 0.0197x 0.0125x , 0.01 < 1 h'/h 1.2
Los datos de la figura 3 se pueden ajustar con un error de hasta ±1.5% con la ecuación
anterior.
Tema 5) Problemas
Tema 5.1) Problemas de revisión: este tipo de problema se enfoca a calcular el gasto q
si todas las demás variables son conocidas, o sea, solo es cuestión de sustituir valores
en las formulas y de búsqueda en las graficas, sin embargo, estos problemas son
necesarios como entrenamiento.
Tema 5.1.1) Problemas de compuertas: ver Figura 1.
P1) Aguas arriba de una compuerta se tiene una carga de altura y1 de 1.4m, la
compuerta tiene un ancho de 0.6m y un abertura de 0.2 m, determine: a) el valor de Q
si la descarga es libre, b) la altura del salto hidráulico yS, c) el valor de Q si aguas abajo
se tiene una altura y3 = 1 m, o sea, la descarga es sumergida.
6
Resolución a). para descarga libre se usa la figura 6.15 y se necesita conocer el valor de
y1/a = 1.4/0.2 = 7, el coeficiente de descarga Cd para la curva de 90º es de alrededor
de 0.585 y por lo tanto el gasto q = Q/b según (3) es:
q = 0.585·0.2·(19.62·1.4)1/2 = 0.613 m2/s y Q = b·q = 0.6·0.613 = 0.368 m3/s
Resolución b). La altura y2 = Cc·a = 0.62·0.2 = 0.124m, el Número de Froude;
Fr22
q2
0.6132
20.1,
gy32 9.81·0.1243
ys
0.124
1 8·20.1 1 0.73m
2
Resolución c). para descarga sumergida se usa la figura 6.16 y se necesita conocer el
valor de y1/a = 1.4/0.2 = 7 y y3/a = 1.0/0.2 = 5, el coeficiente de descarga Cd para 7 en
el eje horizontal corta la curva de curva y3/a = 5 aproximadamente para un Cd = 0.37 y
por lo tanto el gasto q = Q/b según (3) es:
q = 0.37·0.2·(19.62·1.4)1/2 = 0.388 m2/s y Q = b·q = 0.6·0.388 = 0.233 m3/s
Problemas 2 al 6) Estos problemas se resuelven con la metodología del problema 1.
Notas: sobre estos problemas es conveniente señalar que:
1. A pesar del la pequeña carga de altura y1 de hasta 80 cms, el Número de
Froude siempre es alto.
2. La velocidad V2 supera en descarga libre supera al menos 2 veces la velocidad
máxima permisible Vp de la arcilla compactada de 1.7 m/s.
3. El valor de y2 este o no sumergida la compuerta será aproximadamente menor
a lo que se indica en la figura, esto es, para reducir velocidad se debe de crear
artificialmente el salto.
4. El problema 6 indica que no existe solución, el lector al buscar en la figura 6.16
para, y1/a = 0.8/0.2 = 4 que intercepte a la curva, y3/a = 0.4/0.2 = 2, no la
encuentra la intersección. Esto se debe a que y3 < ys, esto es, antes de asignar
un valor arbitrario a y3 se deberá de calcular ys y proponer un valor de y3 que
sea: y3 > 1.10·ys, según Gardea en vez de 1.1 debe ser 1.2 con el objetivo de
limitar la longitud del salto Ls.
5. Es conveniente insistir que si una compuerta se diseña para descargar en
forma sumergida el valor de y3 debe ser: y3 > 1.10·ys.
Tema 5.1.2) Problemas de vertedores: ver Figura 2.
P7) Un vertedor colocado en un canal rectangular de 0.6m de ancho, tiene una altura
del fondo a la cresta de; w = 0.3m, una altura de ola de, h = 0.5m y un espesor de, e =
1.0m. Aguas abajo la altura de la lamina es de, h’ = 0.1m sobre la cresta, con estos
datos determine el valor del gasto Q para las siguientes condiciones:
7
a) El vertedor es de pared delgada (ε1 = 1) y descarga en forma libre (ε2 = 1).
b) El vertedor es de pared gruesa (ε1 < 1) y descarga en forma libre (ε2 = 1).
c) El vertedor es de pared gruesa (ε1 < 1) y descarga en forma sumergida (ε2 < 1).
Resolución a). El calculo de q y Q se basa en la formula (6). Para la opción 1) solo
interviene el coeficiente μ que depende de la contracción (el termino 0.611) y de la
velocidad V1 aguas arriba que no necesariamente es casi cero (el termino 0.08·h/w).
μ = 0.611 + 0.08h/w = 0.611 + 0.08·0.5/0.3 = 0.744
q = (2.952h 3/2)μ·ε1·ε2 = (2.952·0.53/2)·0.744·1·1 = 0.776m2/s
q se multiplica por el ancho b y se obtiene: Q = b·q = 0.6m·0.776m2/s = 0.466m3/s
Resolución b). Si el vertedor es de pared gruesa se genera una presión sobre la cresta
del vertedor que se opone al flujo que proviene de aguas arriba, según Bazin y Gibson
este efecto reduce el gasto por un factor ε1, que se obtiene experimentalmente:
Se calcula e/h = 1.0m/0.5m = 2 para determinar cual formula de (8) se debe de usar y
en este ejemplo corresponde a la de Bazin.
ε1 = 0.7 + 0.185/(e/h) = 0.7 + 0.185/2 = 0.792
El gasto de 0.466m3/s obtenido en a) se multiplica por 0.792 y se obtiene el gasto en el
vertedor de pared gruesa; Q = 0.466m3/s·0.792 = 0.369m3/s
Resolución c). Si el vertedor opera en forma sumergida el problema es un tanto
complejo, sin embargo, según Domínguez esta sumersión reduce el gasto por un factor
ε2, y que se presenta en la tabla o la grafica en la Figura 3.
Se calcula 1 - h’/h = 1 – 0.1/0.5 = 0.8 y se busca en la tabla2 de la Figura 3 y se
encuentra que ε2 = 0.96.
El gasto de 0.369m3/s obtenido en b) se multiplica por 0.96 y se obtiene el gasto que
incluye el efecto de la sumersión; Q = 0.369m3/s·0.96 = 0.354m3/s
Problemas 8 al 12) Estos problemas se resuelven con la metodología del problema 1.
/2
Nota: si no encuentra el valor de (1 - h’/h) en la tabla y se desea evitar la interpolación se
puede recurrir a la grafica.
8
Tema 5.1) Problemas de diseño: este tipo de problema se enfoca al cálculo de la
abertura a de la compuerta y de {w y h} en el vertedor. Además si la compuerta y el
vertedor están relacionada a través del salto hidráulico parte de la información que se
obtenga en la compuerta será necesaria para el diseño del vertedor o viceversa.
P13, Diseño en descarga libre) Una compuerta tiene una carga de altura aguas arriba
de 1.2m, un ancho de 0.6m y debe descargar un gasto de 0.3m3/s (q = Q/b = 0.5m2/s).
El diseño consiste en una descarga libre en la sección 2 y para controlar el salto
hidráulico se coloca aguas abajo un vertedor de pared delgada con descarga libre,
determine: 1) la abertura de la compuerta, 2) la altura del vertedor w, 3) la distancia a
la que se coloca el vertedor a partir de la compuerta.
Resolución a): De la formula (3) se despeja a y se deja en términos de Cd;
a
1
q
1
0.5
0.103
Cd 2gy1 Cd 19.62·1.2
Cd
El cálculo de Cd es un proceso iterativo que inicia al asumir que Cd = 0.58, en el
entendido que Cd esta en el rango de [0.55, 0.60] según se observa en la Figura 6.15.
Este proceso iterativo presentado en forma de
tabla conduce rápidamente a la solución de la
abertura a de la compuerta y el proceso
iterativo termina cuando el valor de a no difiera
en 0.01m entre la iteración k versus k-1.
En la 1ª iteración se obtiene que la abertura de
la compuerta es: a = 0.178m
La profundidad en la sección 2 es: y2 = Cc·a = 0.62*0.178 = 0.11m y el área del chorro,
A2 = b·y2 = 0.6·0.11 = 0.066m2 y la velocidad, V2 = Q/A2 = 0.3/0.066 = 4.55m/s. Calcular
la V2 simplifica el calculo de Fr22
Se calcula el Número de Froude en la sección 2, que para una sección rectangular es:
Fr22
q2
V22
4.552
19.14
gy32 gy2 9.81·0.11
El salto hidráulico resulta ser:
ys y 3
y2
0.11
1 8Fr22 1
1 8·19.14 1 0.63m
2
2
Conocida la profundidad y3 y de acuerdo a la figura 3; y3 = 0.63 = w + h y por lo tanto
w = y3 – h, la ecuación del vertedor de pared delgada con descarga libre resulta ser:
9
h
q / 2.952
2/3
h
0.611 0.08 y - h
3
2/3
C1
μ
0.667
(9)
C1 = (0.5/2.952)0.667 = 0.306m y μ = 0.611 + 0.08[h/(0.63 – h)]
Si se asume que el primer valor de μ es: μ = 0.7 el siguiente proceso iterativo
presentado en forma de tabla conduce rápidamente a la solución, cuando h entre la
iteración k y la k-1 sea menor de 0.01m. Donde C1 = 0.306m.
Donde h se obtiene en al 2ª iteración y es igual a
0.378m y w;
w = 0.63 – 0.378 = 0.252m
La colocación del vertedor a partir de la compuerta aguas abajo es:
a/Cc + 6(y3 – y2) = 0.178/0.62 + 6·(0.63 – 0.11) = 3.41m
P14, diseño en descarga sumergida) Se desea que la compuerta del P13) opere en
forma sumergida sobre esta base, a) diseñe de nuevo el vertedor, b) calcule la abertura
de la compuerta.
Resolución a). En el tema 5.1.1 y en las notas 4 y 5 se indica que si la compuerta debe
de operar en forma sumergida la profundidad y3 > 1.1·ys para este diseño se propone
que y3 = 1.15·ys, por lo tanto,
y3 = 1.15·0.63 = 0.7245 ≈ 0.73m (redondeando al superior)
Para el diseño del vertedor se parte de procedimiento que se indica en la formula (9),
solo que en vez de usar 0.63m, se usa y3 = 0.73m
h
q / 2.952
2/3
h
0.611 0.08 y - h
3
2/3
C1
μ
0.667
(9)
C1 = (0.5/2.952)0.667 = 0.306m y μ = 0.611 + 0.08[h/(0.73 – h)]
Si se asume que el primer valor de μ es: μ = 0.7 el siguiente proceso iterativo
presentado en forma de tabla conduce rápidamente a la solución, cuando h entre la
iteración k y la k-1 sea menor de 0.01m. Donde C1 = 0.306m.
Donde h se obtiene en al 1ª iteración y es igual a
0.388m y w;
w = 0.73 – 0.388 = 0.342m
10
Calcular exactamente la abertura de la compuerta en descarga sumergida a partir del
diagrama de Cofré es un proceso por ensayo y error bastante largo para superar esta
dificultad es más conveniente proceder de la siguiente forma:
Como se conoce que la abertura de la compuerta a = 0.178m para descarga
libre la abertura en descarga sumergida debe ser mayor por lo tanto;
Se incrementa de 10% en 10% la abertura de 0.178m (0.178·0.1 ≈ 0.02m) y se
calcula el Cd para a = 0.20m, 0.22m, 0.24m y con esto el gasto Q hasta que se
aproxime a Q = 0.30m3/s.
Calculo: Q Cdba 2gy1 Cd·0.6a 19.62·1.2 2.91Cd·a , en forma de tabla el calculo
queda de la siguiente forma;
En dos intentos se obtiene el resultado y
este indica que la compuerta se debe de
abrir aproximadamente 0.21m.
Observaciones sobre el diseño en descarga sumergida: Para diseñar una compuerta
en descarga sumergida se debe primero: calcular la descarga libre hasta el cálculo del
salto hidráulico por dos razones:
La altura del salto ys determina la altura y3.
Es necesario conocer la abertura de la compuerta en descarga libre para tener
una idea cual será la abertura en descarga sumergida.
P15, Diseño en descarga sumergida) Una compuerta tiene una carga de altura aguas
arriba de 2.4m, un ancho de 0.9m y debe descargar un gasto de 0.9m3/s (q = Q/b =
1.0m2/s). El diseño consiste en una descarga sumergida en la sección 2 y para controlar
el salto hidráulico se coloca aguas abajo un vertedor de pared delgada con descarga
libre. La sumersión debe ser y3 = 1.20·ys (redondear a centímetros), determine:, 1) la
altura del vertedor w, 2) la abertura de la compuerta en descarga sumergida.
Sugerencia: siga el procedimiento del problema 14.
Respuesta: ys queda de ≈ 1.085, 1) w ≈ de 0.68m, 2) a de ≈ 0.297m.
P16, Diseño en descarga sumergida) Una compuerta tiene una carga de altura aguas
arriba de 1.20 m, un ancho de 0.6m y debe descargar un gasto de 0.3m3/s (q = Q/b =
0.5m2/s). El diseño consiste en una descarga sumergida en la sección 2 y para controlar
el salto hidráulico se coloca aguas abajo un vertedor de pared delgada con descarga
libre. La sumersión debe ser y3 = 1.2·ys (redondear a centímetros), determine:, 1) la
altura del vertedor w, 2) la abertura de la compuerta en descarga sumergida.
Respuesta: ys queda de ≈ 0.63, 1) w ≈ 0.365m, 2) a ≈ 0.224m.
11
P17, Diseño en descarga libre) Una compuerta tiene una carga de altura aguas arriba
de 3.0m, un ancho de 1.2m y debe descargar un gasto de 2.4m 3/s (q = Q/b = 2.0m2/s).
El diseño consiste en una descarga libre en la sección 2 y para controlar el salto
hidráulico se coloca aguas abajo un vertedor de pared delgada con descarga libre,
determine:, 1) la abertura de la compuerta en descarga libre, 2) la altura del vertedor
w, 3) la distancia a la que se debe de colocar el vertedor a partir de la compuerta.
Respuesta: 1) a = 0.44 a 0.45m, 2) w = de 0.63 a 0.65m, 3) Ls = de 8 a 9m.
P18, de revisión) Un canal de riego (con m = 1) requiere de una profundidad y1 = 2.0m
para extraer Q1 = 0.5m3/s de las compuertas laterales. Esta altura se obtiene al colocar
un vertedor de pared gruesa. Aguas abajo del vertedor la corriente de agua con QT
continua y se necesita que la altura siga siendo 2.0m ya que 1,000m más adelante se
colocaran de nuevo 2 compuertas.
Figura 4. Vertedor de pared gruesa operando con descarga sumergida.
Si e = 2.0m, w = 0.62m y h’ = 0.5m y el ancho b = 10.0m, obtenga el valor del gasto
total QT que se descarga y el desnivel Δz entre el canal 1 y el canal 2. Use el método de
solución indicado en el problema 7.
Respuesta: QT entre 28 a 30 m3/s, Δz = 0.88m.
P19, de diseño con descarga libre). Para el problema anterior con un gasto Q = 29
m3/s y b = 10.0 m, determine a) h y w si el vertedor es de pared delgada y tiene una
descarga libre h’ = 0, b) el valor de Δz.
Respuesta: a) h ≈ 1.21m y w ≈ 0.79, b) Δz = 2 – 0.79 = 1.21m.
P20, Calculo de la contracción) Un deposito descarga a través de un Tubo de Borda
que tiene un área AT/3, sin embargo, es observable que en la salida, en el punto 3, el
área de conducción A3, disminuye. Usando las Tres ecuaciones fundamentales de la
Hidráulica: Continuidad y Gasto, Energía e Impulso encuentre el valor de A3 en
términos del área del tubo AT.
/3
La Toma de Borda consiste en un tubo que entra en el deposito, esto permite suponer que la
fuerza que empuja al agua a meterse dentro del tubo es F = γў·AT, donde ў es el centroide
del área AT medida a partir de la superficie libre del deposito
12
Figura 5. Elementos que intervienen en una descarga de la Toma de Borda.
Resolución: Considerando que las perdidas de 1 a 3 son cero (h13 = 0) la velocidad en la
descarga (punto 3) se obtiene de la ecuación de Bernoulli y es V3 2g·y y el gasto Q
de la ecuación de continuidad; Q = V3A3, como el área A3 es desconocida la respuesta
al valor de esta variable se puede obtener o no en la ultima ecuación de la Hidráulica
que es la Impulso, al plantear esta ecuación de 2 a 3 se tiene:
γ
Fp2 Fp3 Q V3 V2
g
Considerando que: V2 = 0, Fp3 = 0, Q = V3A3 la ec. anterior se reduce a;
γ
γ
Fp2 V3A3 V3 0 V32 A3
g
g
Sustituyendo a; Fp2 γ·y·AT y V3 2g·y en la ec. anterior se obtiene;
γ
Fp2 γ·y·AT 2gy A3 2γ·yA3
g
2
Eliminando γy y despejando A3 se obtiene:
A3
1
AT Cc ·AT
2
Por lo tanto se puede concluir que el área total del tubo AT se contrae a la mitad a la
salida del tubo, o sea, el Coeficiente de Contracción = 0.5.
Interpretación Física de la contracción: La ecuación de Bernoulli indica que hay sufí-ciente
energía para generar una velocidad V3 2g·y en la descarga ,sin embargo, al incluir
la ec. de Impulso en el análisis indica que no hay fuerza de presión suficiente para
sacar todo el gasto Q = V3AT, por el orificio del tubo.
13